基于Rimoldi分解的连续相位调制信号Turbo频域均衡算法

钟 凯 彭 华 葛临东



基于Rimoldi分解的连续相位调制信号Turbo频域均衡算法

钟 凯*彭 华 葛临东

(解放军信息工程大学信息系统工程学院 郑州 450002)

针对高阶部分响应连续相位调制(CPM)信号均衡中存在的复杂度高和性能较差等问题，该文从Rimoldi分解的角度出发，设计了一种新的适用于倾斜相位CPM信号的发射帧结构，并在此基础上结合单载波频域均衡(FDE)和Turbo均衡的思想，提出了一种适用于高阶CPM信号的Turbo频域均衡算法。该算法通过将信号均衡转化到频域进行处理，避免了时域均衡算法在计算均衡器系数时存在的大矩阵求逆问题，同时使用Turbo均衡的软信息迭代处理来改善系统的性能。理论分析和仿真结果表明，对于四阶部分响应CPM信号，在存在严重符号间干扰的多径衰落信道的条件下，该算法与现有的基于符号的频域均衡算法相比，在保持较低复杂度的同时，具有大约1.5 dB的性能增益。

无线通信；连续相位调制；多径衰落信道；Rimoldi分解；单载波频域均衡；Turbo均衡

1 引言

连续相位调制(Continuous Phase Modulation, CPM)是一种具有恒定包络的先进调制技术[1]。在高斯白噪声(AWGN)信道下，编码CPM具有恒包络、高功率和带宽利用率等一系列优异性能。但是在60 GHz毫米波通信系统中，CPM信号在多径衰落信道下传输，由于编码CPM系统的迭代检测依赖于CPM符号间的记忆特性，使得码间干扰对系统性能的影响非常严重，因此采取有效的均衡措施来减少符号间干扰显得尤为重要。

文献[2]提出将单载波频域均衡思想运用于CPM信号处理，提出了基于Gram-Schmidt正交分解法和Laurent分解法的两种频域均衡算法。文献[3]在此基础上引入判决反馈，前馈滤波在频域实现，反馈滤波则在时域实现，有效改善了均衡算法的性能。文献[4]进一步给出了MMSE均衡器的简化方法，针对均衡算法中出现的大矩阵求逆问题进行简化处理，可以有效降低均衡器的复杂度。文献[5]研究了一种差分预编码CPM信号，与非预编码相比，在相同环境下对预编码信号进行频域均衡解调，其误码率减半。文献[6]针对二阶部分响应连续相位调制信号的频域均衡技术，提出了一种基于Laurent分解的CPM迭代检测算法，有效降低了频域均衡算法的复杂度，但是对于严重的多径衰落信道，算法性能有着较大的损失。文献[7]和文献[8]分别研究了单载波和多载波频域均衡系统的CPM混沌迭代方案，通过改变发送采样序列的顺序，降低了采样点之间的相关性，获得较好的性能改善。文献[9]对CPM频域均衡的数据块结构中需要插入的内缀长度给出了具体的定义，并从CPM信号相位状态星座图的角度，给出了形象的解释。文献[10]对多指数CPM信号基于频域均衡接收机的设计进行了研究，设计了一种适用于多指数CPM信号的帧结构。

本文研究了基于Rimoldi分解[11]的CPM信号均衡技术，针对高阶CPM信号的频域均衡，设计了一种新的适用于倾斜相位网格的发射信号帧结构，并在此基础上运用Turbo均衡[12,13]思想，提出了一种新的基于Turbo频域均衡的高阶CPM信号均衡算法，与基于符号的频域均衡算法[6]相比，对于严重的多径衰落信道，在保持相对较低复杂度的情况下，有效地提高了系统性能，并且对于高阶CPM信号系统性能的改善更明显。

2 系统模型

2.1 CPM信号模型

连续相位调制等效复基带信号表达式为

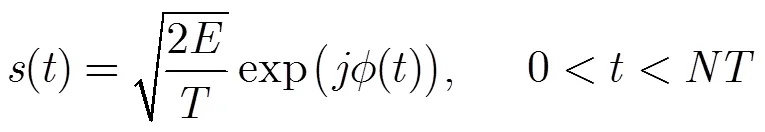
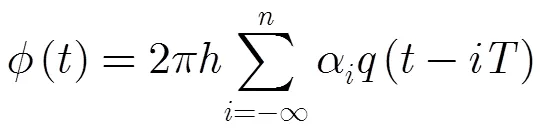
2.2 M阶CPM信号的Rimoldi分解

根据文献[10]中提出的Rimoldi分解表述，CPM调制器可以表示为连续相位编码器(Continuous Phase Encoder, CPE)和无记忆调制器(Memoryless Modulator, MM)的组合，CPE使用CPM信号的倾斜相位描述

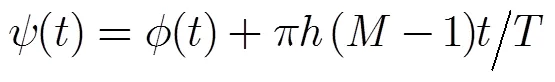
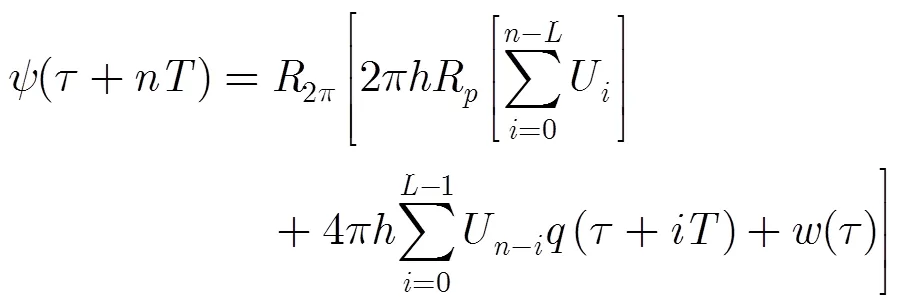
由式(1)，式(3)和式(5)可以得到基带实际CPM信号与基带倾斜相位CPM信号之间的关系为

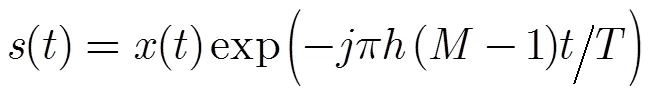
2.3 系统及信道模型

基于Rimoldi分解进行Turbo频域均衡的CPM迭代检测系统框图如图1所示。

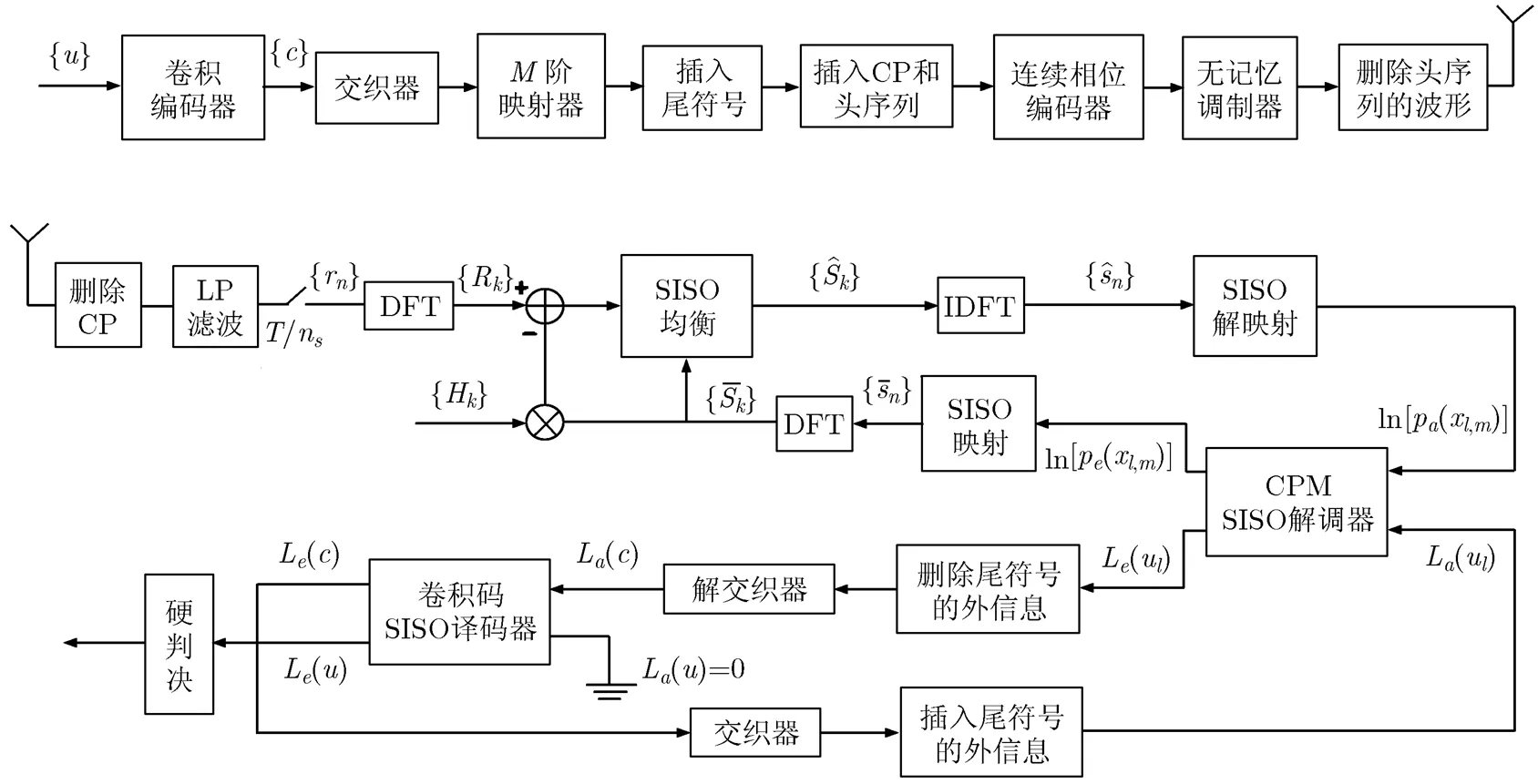
图1 发射机和接收机的系统框图

CPM信号经过有限长度符号间隔的多径衰落符号间干扰(ISI)信道，接收信号可以表示为

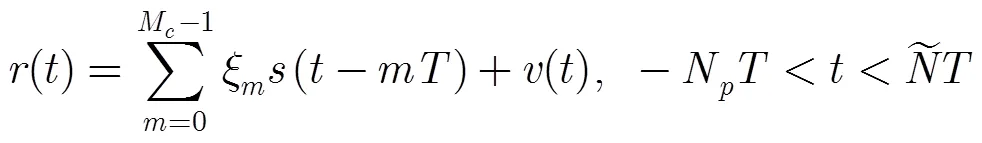
接收信号经过删除循环保护间隔、低通滤波以及采样，式(7)变为

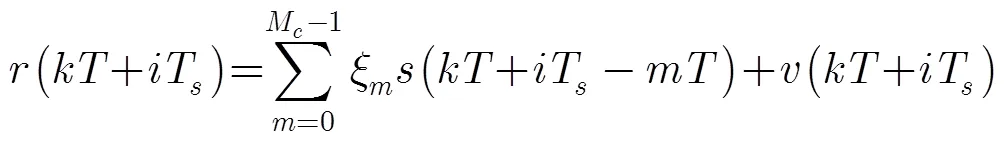
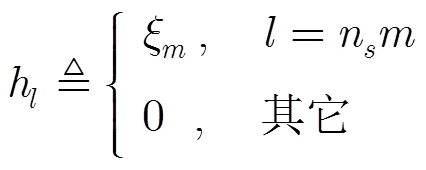
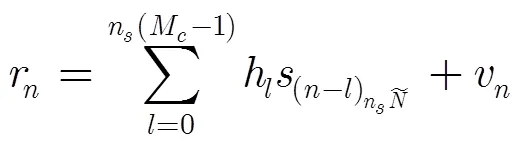
由式(10)可以进一步得到

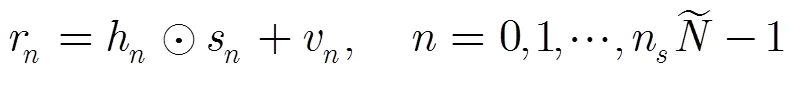
3 倾斜相位CPM信号帧结构设计

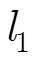
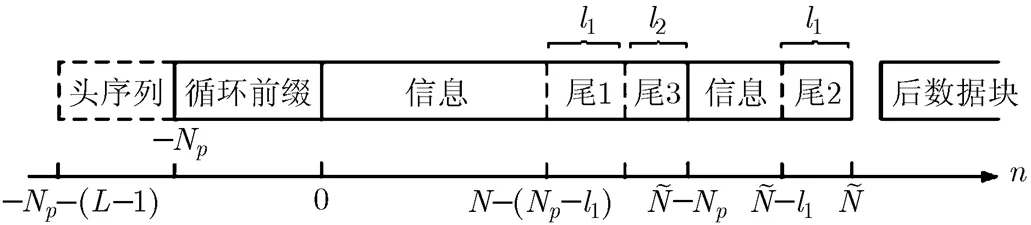
图2 倾斜相位CPM信号的发射帧结构

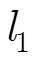
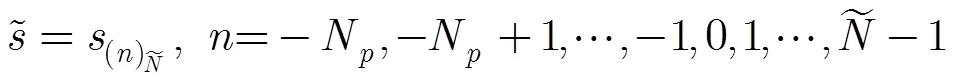
4 CPM 信号Turbo频域均衡

4.1 SISO均衡

文献[12]中提出了一种修正软干扰抵消(Soft Interference Canceller, SIC) Turbo均衡器，其结构如图3所示。

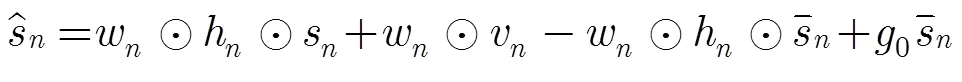
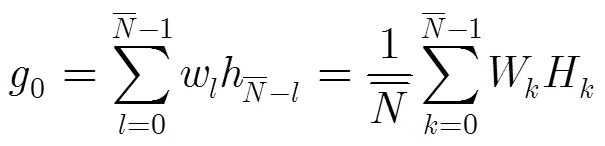
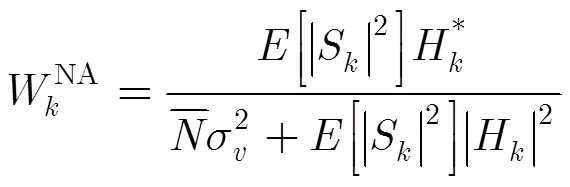
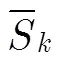
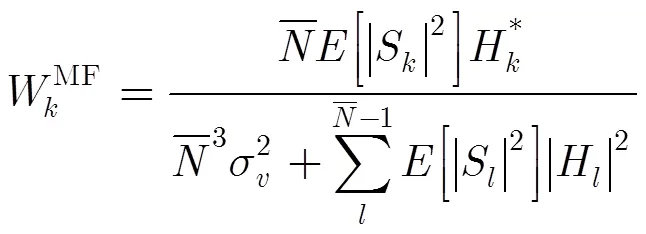
4.2 SISO映射

4.3 SISO解映射

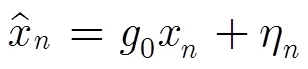
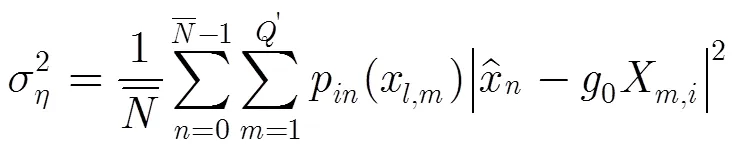
从而可以得到SISO解映射输出的CPM码字符号先验信息的归一化表达式为

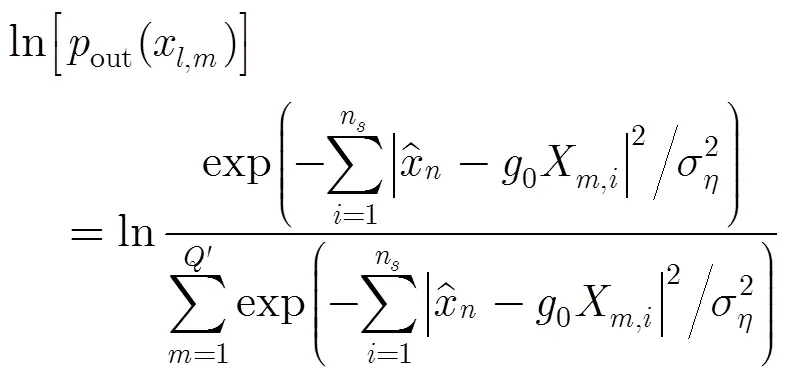
5 复杂度分析

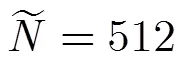
表1本文算法与基于符号频域均衡算法的复杂度比较

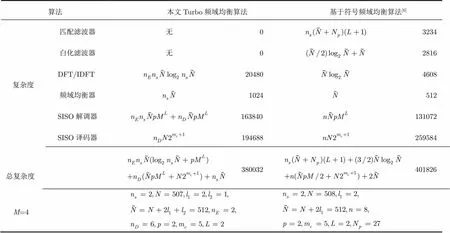
算法 本文Turbo频域均衡算法 基于符号频域均衡算法[6] 复杂度匹配滤波器无 0 3234 白化滤波器无 0 2816 DFT/IDFT 20480 4608 频域均衡器 1024 512 SISO解调器163840 131072 SISO译码器 194688 259584 总复杂度380032401826 M=4

6 仿真实验

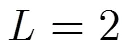
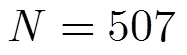
图4给出了在Tu-6信道条件下对2RC4CPM信号进行仿真得到的实验结果。设定均衡迭代次数分别为1, 2和3，每次均衡迭代后进行3次解调译码迭代。从图4中可以看出，当均衡迭代次数达到2次时，已经可以取得较好的性能，迭代次数为3次时，性能有小幅提升，但系统复杂度增加较大，因此实际应用中通常选择均衡迭代次数为2。

7 结束语

本文从Rimoldi分解的角度出发，结合单载波频域均衡技术和Turbo均衡思想，提出了一种适用于高阶CPM信号的Turbo频域均衡算法。仿真结果表明，该算法在存在严重符号间干扰的多径衰落信道下，保持较低复杂度的同时，具有良好的性能。下一步的工作将考虑研究信道条件未知情况下的盲均衡算法。

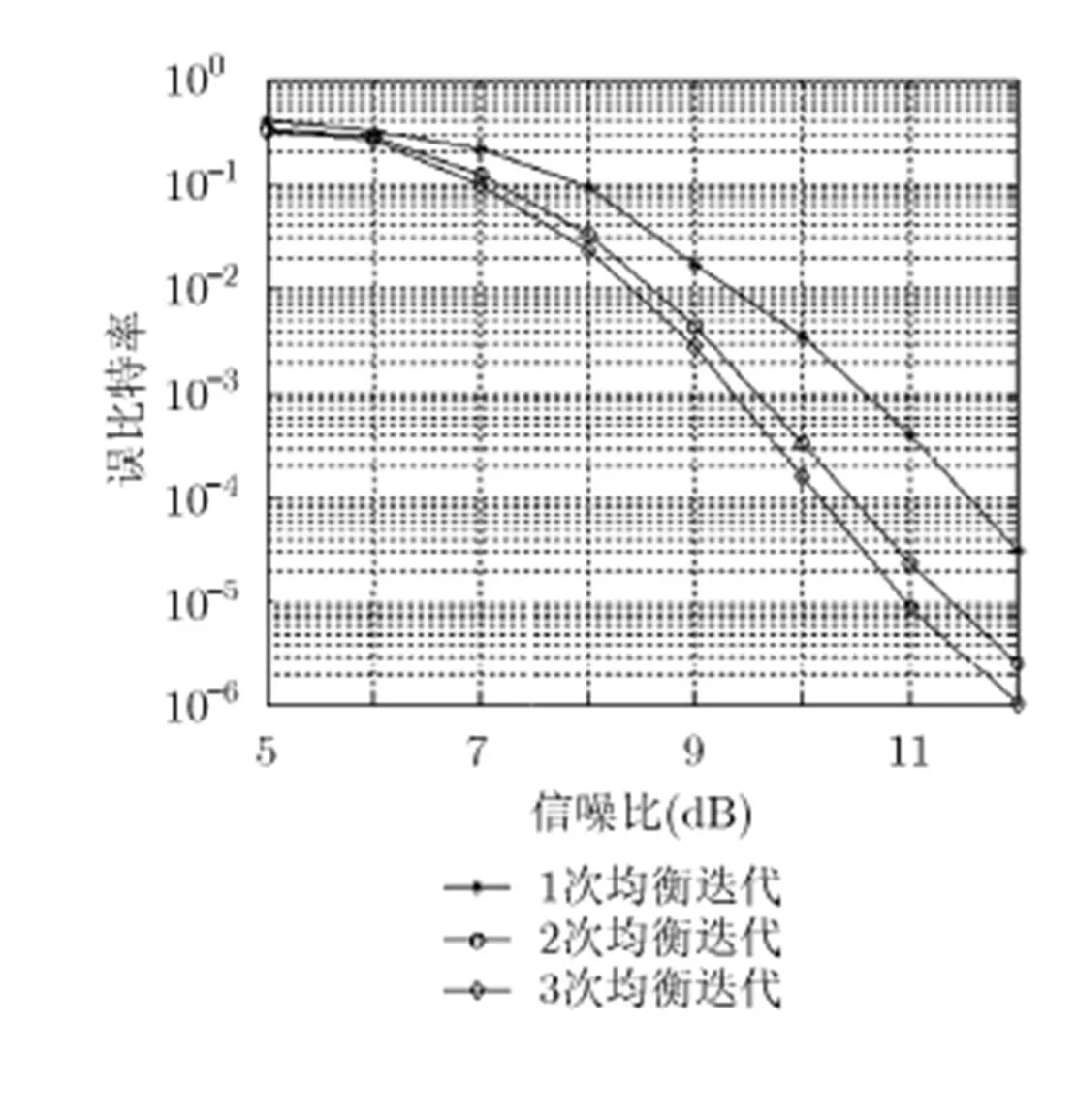
图4 不同均衡迭代次数对系统性能的影响

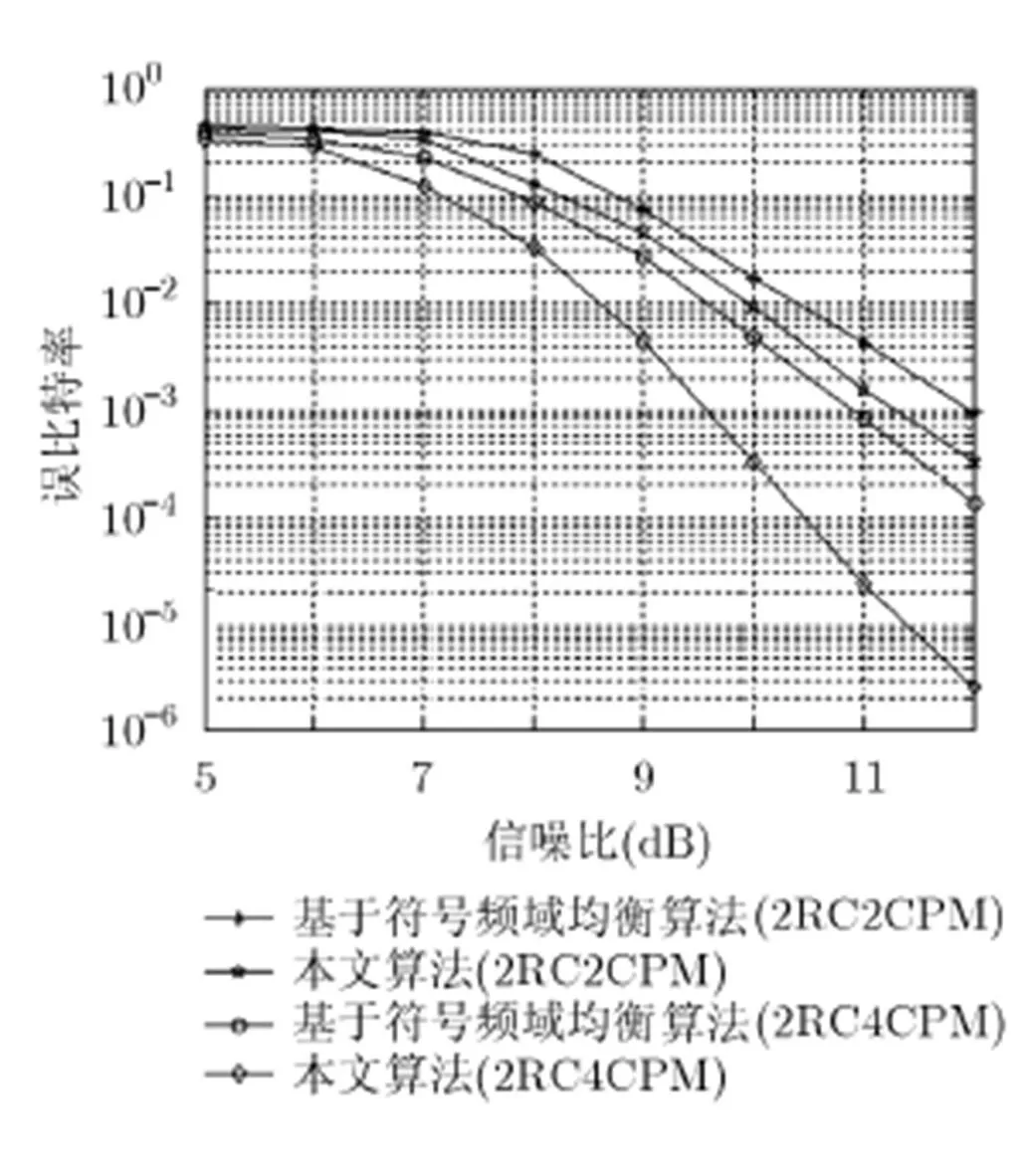
图5 不同调制阶数CPM信号两种算法的性能比较

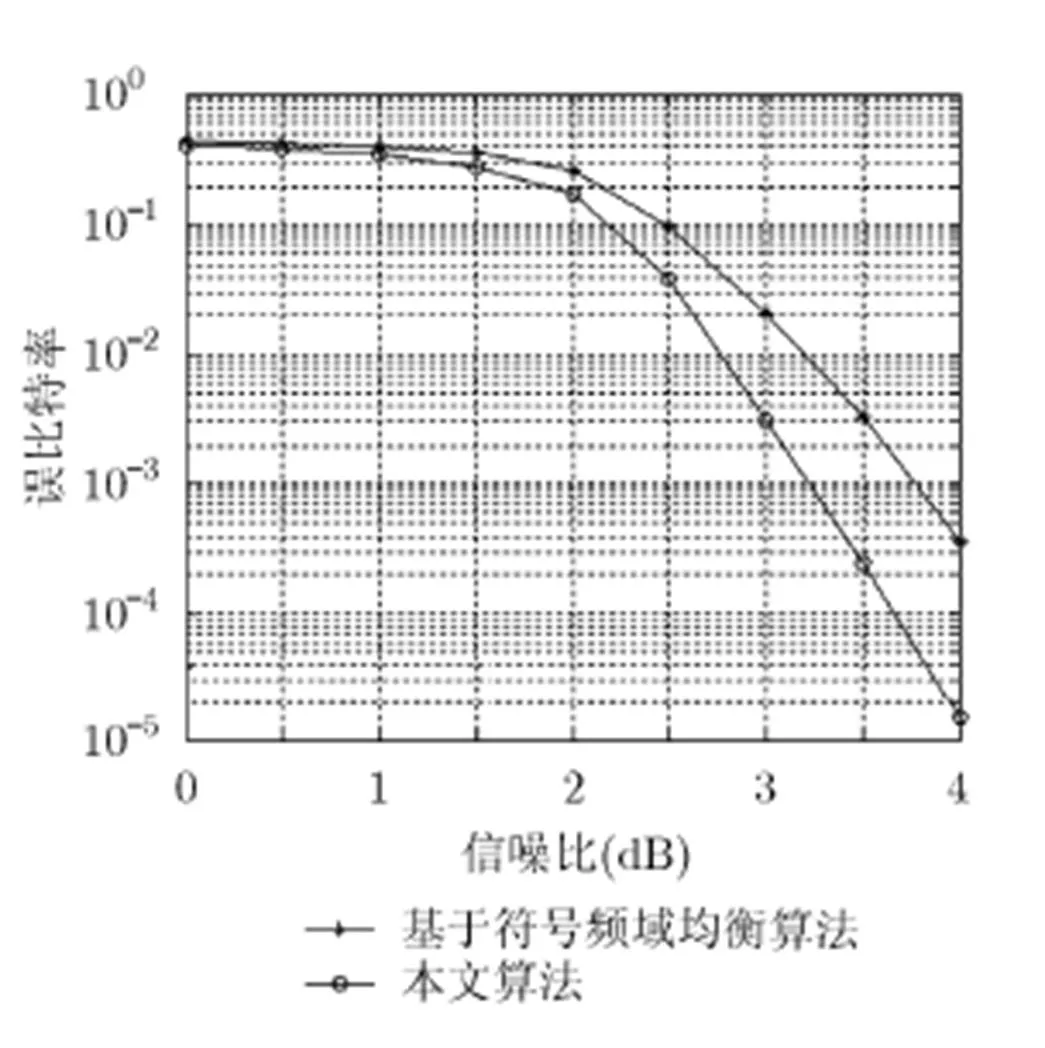
图6 Proakis’A信道下两种算法的性能比较

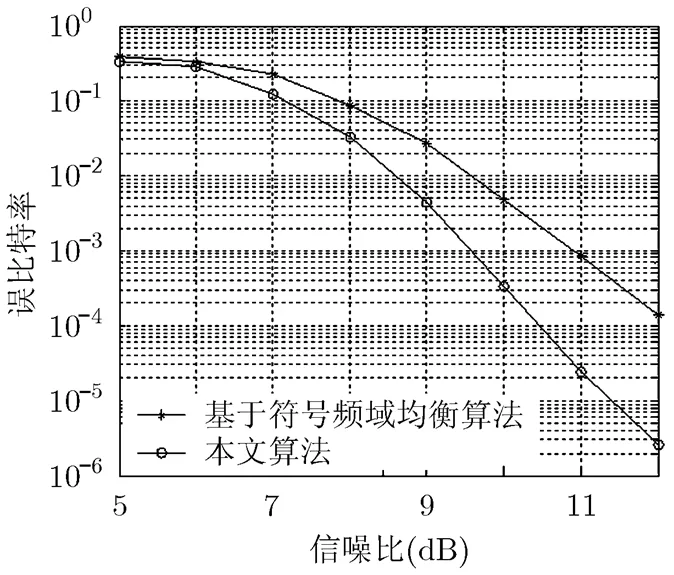
图7 Tu-6信道下两种算法的性能比较

[1] Hosseini E and Perrins E. The Cramer-Rao bound for training sequence design for burst-mode CPM[J]., 2013, 61(6): 2396-2407.

[2] Tan J and Stuber G L. Frequency-domain equalization for continuous phase modulation[J]., 2005, 4(5): 2479-2490.

[3] Pancaldi F and Vitetta G M. Equalization algorithms in the frequency domain for continuous phase modulations[J]., 2006, 54(4): 648-658.

[4] Thillo W V and Horlin F. Low-complexity linear frequency domain equalization for continuous phase modulation[J]., 2009, 8(3): 1435-1445.

[5] Thillo W V and Horlin F. Novel Block Constructions using an Intrafix for CPM with Frequency Domain Equalization[J]., 2010, 9(3): 951-955.

[6] 李强, 严庆, 罗胜. 基于符号频域均衡的CPM迭代检测算法[J]. 电子与信息学报, 2011, 33(7): 1550-1555.

Li Qiang, Yan Qing, and Luo Sheng. Iterative detection algorithm based on symbol frequency domain equalization for continuous phase modulation[J].&, 2011, 33(7): 1550-1555.

[7] Hassan E S, Zhu X, and Khamy S E. A chaotic interleaving scheme for the continuous phase modulation based single-carrier frequency-domain equalization system[J]., 2012, 62(1): 183-199.

[8] Hassan E S, Zhu X, and Khamy S E. Chaotic interleaving scheme for single- and multi-carrier modulation techniques implementing continuous phase modulation[J]., 2013, 28(7): 770-789.

[9] Thillo W V, Ramon V, and Nsenga J. Supplementary proof for “Equalization algorithms in the frequency domain for continuous phase modulations”[J]., 2012, 60(1): 27-29.

[10] Saleem S and Stuber G L. Linear Diophantine constrained intra-fix for frequency domain equalization of multi-h CPM[J]., 2012, 60(8): 2265-2274.

[11] Rimoldi B E. A decomposition approach to CPM[J]., 1988, 34(2): 260-270.

[12] Laot C, Bidan R L, and Leroux D. Low-complexity MMSE turbo equalization: a possible solution for EDGE[J]., 2005, 4(3): 965-974.

[13] Tüchler M, Singer A C, and Koetter R. Turbo equalization: principles and new results[J]., 2002, 50(5): 754-767.

[14] Tüchler M, Singer A C, and Koetter R. Minimum mean squared error equalization using a priori information[J]., 2002, 50(3): 673-683.

钟 凯： 男，1987年生，博士生，研究方向为通信信号处理、编码调制.

彭 华： 男，1973年生，教授，博士生导师，研究方向为通信信号处理、软件无线电.

葛临东： 男，1946年生，教授，博士生导师，研究方向为通信信号处理、软件无线电.

Turbo Frequency Domain Equalization Algorithm Based on Rimoldi Decomposition for Continuous Phase Modulation Signals

Zhong Kai Peng Hua Ge Lin-dong

(,,450002,)

To solve the issues of the high complexity and poor performance in the equalization of high order and partial response Continuous Phase Modulation (CPM) signals, a new framework of tilted phase CPM transmitted signals is designed from the perspective of Rimoldi decomposition. A novel frequency domain equalization algorithm for high order CPM signals is proposed based on the combination of single-carrier Frequency Domain Equalization (FDE) and Turbo equalization. This algorithm avoids the large matrix inversions in computation of the equalizer coefficients in time domain by transforming the signal equalization to frequency domain. Simultaneously, it improves the system performance by soft information iterative process. The analysis and simulation results show that in multipath fading channels with serious inter-symbol interference the proposed algorithm provides a relatively lower computational complexity and a performance gain of about 1.5 dB in signal-noise ratio compared with the previously proposed FDE algorithm based on symbol for fourth-order and partial response CPM signals.

Wirelesscommunication;Continuous Phase Modulation (CPM); Multi-path fading channel; Rimoldi decomposition; Single-carrier Frequency Domain Equalization (FDE); Turbo equalization

TN92

A

1009-5896(2014)05-1190-06

10.3724/SP.J.1146.2013.00990

钟凯 zhongkai8686@163.com

2013-07-08收到，2013-10-22改回

国家自然科学基金(61072046)和河南省基础与前沿项目(102300410008)资助课题