强约束优化降维MUSIC二维DOA估计

蔡晶晶 鲍 丹 李 鹏 赵国庆



强约束优化降维MUSIC二维DOA估计

蔡晶晶*鲍 丹 李 鹏 赵国庆

(西安电子科技大学电子信息攻防对抗与仿真技术教育部重点实验室 西安 710071)

该文针对2维DOA估计运算量大的问题，提出一种改进的降维MUSIC(MRD-MUSIC)算法。MRD-MUSIC算法利用二次优化方法将2维DOA估计分解为两级1维DOA估计，从而大大降低了运算量。其中采用对优化函数直接求导的方式求解问题函数，使方向向量得到了较强约束，因此求解结果更加接近最优解。仿真实验验证了算法的正确性，角度估计运算效率高，无角度配对过程，且具有较高的成功率与精确度。

2维波达方向估计；降维MUSIC算法；优化算法

1 引言

利用经典MUSIC算法进行2维DOA估计时需要进行2维谱峰搜索，运算量巨大，实际应用价值较低，因此高效的2维DOA估计是该领域内的研究热点问题。文献[11]中先利用互协方差矩阵求解俯仰角，再用自动配对法求解方位角，该算法角度估计精度略低于MUSIC算法。文献[12]构建了阵列的空间圆锥曲面来波估计模型，通过两条直线阵RBF神经网络模型估计两个空间圆锥曲面，两曲面相交线即为2维来波方向，该方法的实现需要大量训练样本集。文献[13]通过降低子空间维数达到提高运算效率的目的，并利用Capon算法进行角度估计，但该方法只适用于单站MIMO雷达1维DOA估计。文献[14]利用噪声子空间及其共轭的交集进行奇异值分解实现噪声子空间的降维，并基于降维噪声子空间与导向矢量及其共轭的双正交性提出快速2维DOA估计算法，该算法仅将运算量降低了50%。文献[15]算法可估计多于阵元数的信源，先对3个子阵特征分解分别进行子空间估计，再进行2维DOA和初始相位的配对，该算法通过对3个子阵的并行处理提高运算速度，但总体运算量并未降低，所需运算成本仍较大。文献[16]针对MIMO雷达DOA和DOD估计问题提出了降维MUSIC(RD-MUSIC)算法，该算法利用二次优化方法将2维DOA估计分解为两级1维DOA估计，仅需做1维谱峰搜索且无需角度配对过程，可大大缩减原算法运算量。然而经分析后发现，RD-MUSIC算法的估计成功率与精确度不是很理想，有待进一步提高以满足实际应用的需求。

本文对降维MUSIC(RD-MUSIC)方法进行了深入分析，提出一种改进的基于直接求导法的降维MUSIC算法，其在保持了与文献[16]基本相同的低运算量的前提下，进一步提高了角度估计的成功率与精确度。该算法中使用了对目标函数直接求导的方法求解角度值，该方法能有效增强对方向向量中各元素应满足条件关系的约束，使求解结果更加接近最优解。最后对该算法进行仿真实验，实验结果验证了本文算法比文献[16]中同类降维MUSIC算法具有更加理想的角度估计性能。

2 阵列信号模型

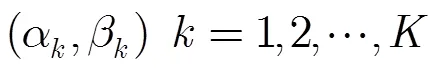
假设各阵元上的噪声为加性高斯白噪声，且与信号不相关。以坐标原点阵元为参考阵元，则该阵列结构中某阵元的输出结果可表示为

图1 信号入射到天线阵列示意图

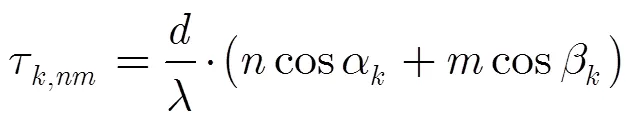
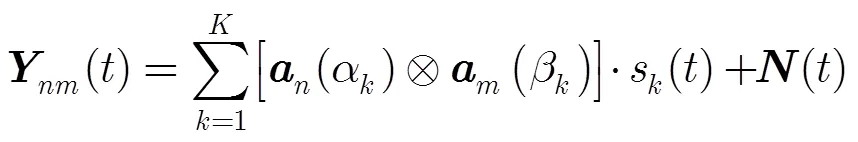
其中入射信号分别与轴、轴夹角的方向向量表示为

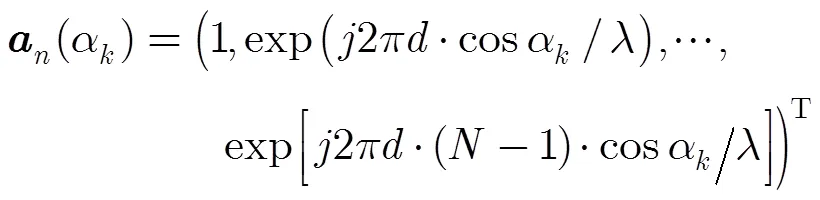
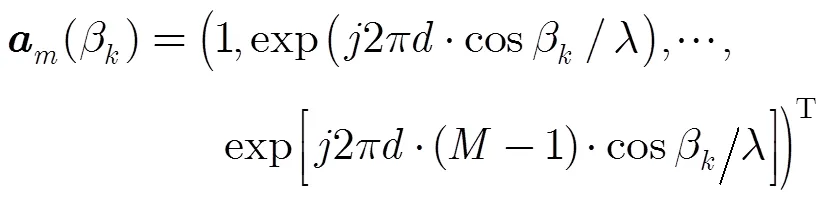
3 降维MUSIC(RD-MUSIC)算法

根据阵列信号模型，可得阵元接收信号的协方差矩阵为

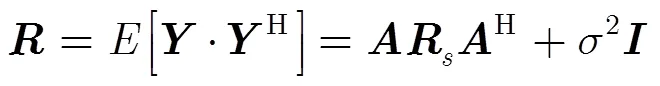
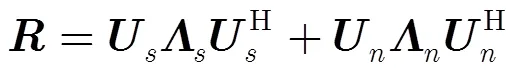
传统2维MUSIC算法的空间谱估计公式[16]为

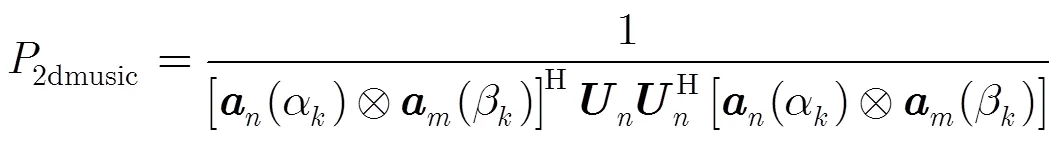
求解式(8)需要进行2维角度搜索，运算量较大，如果能够将该求解问题用1维搜索运算求得，运算量将大大降低，或者也可称之为降维。

为了将2维角度估计问题降维解之，首先将其转化为二次优化问题，定义检测量为

将式(9)做如下变形：

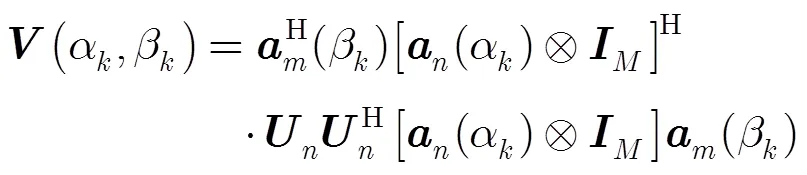
令

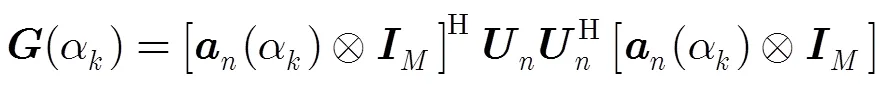
则2维DOA估计问题可等价为求解：

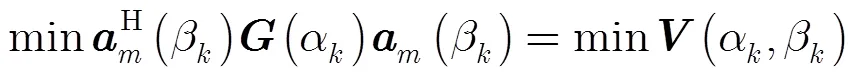
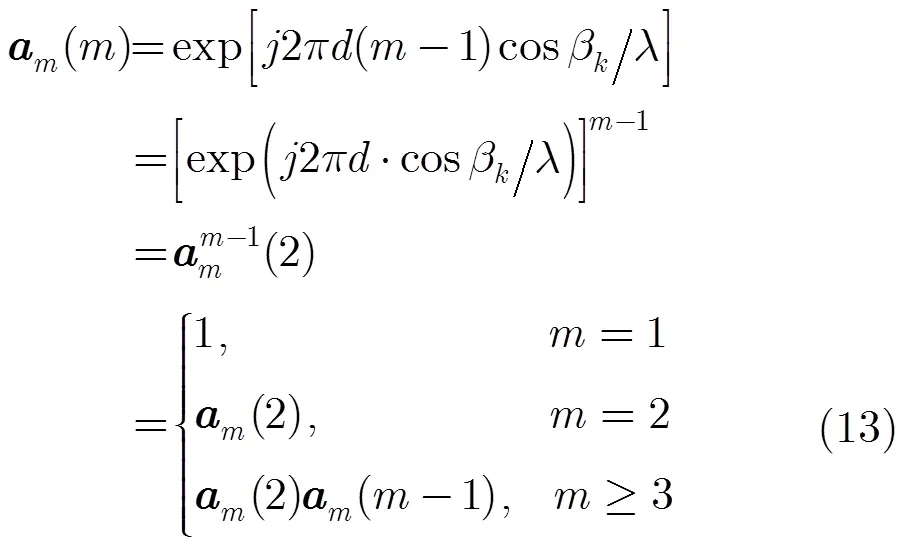
4 改进的降维MUSIC(MRD-MUSIC)算法

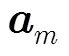
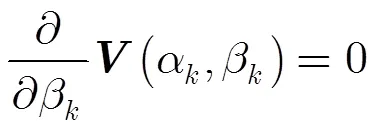
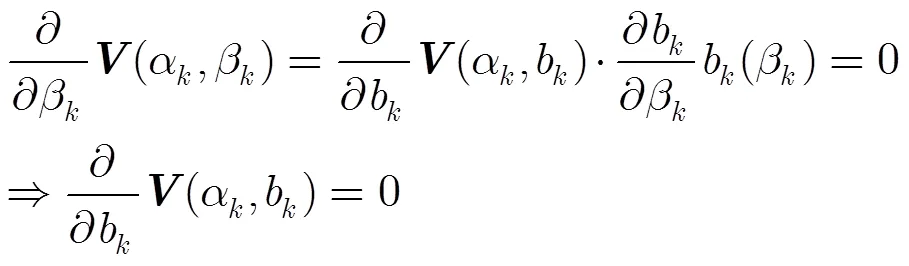
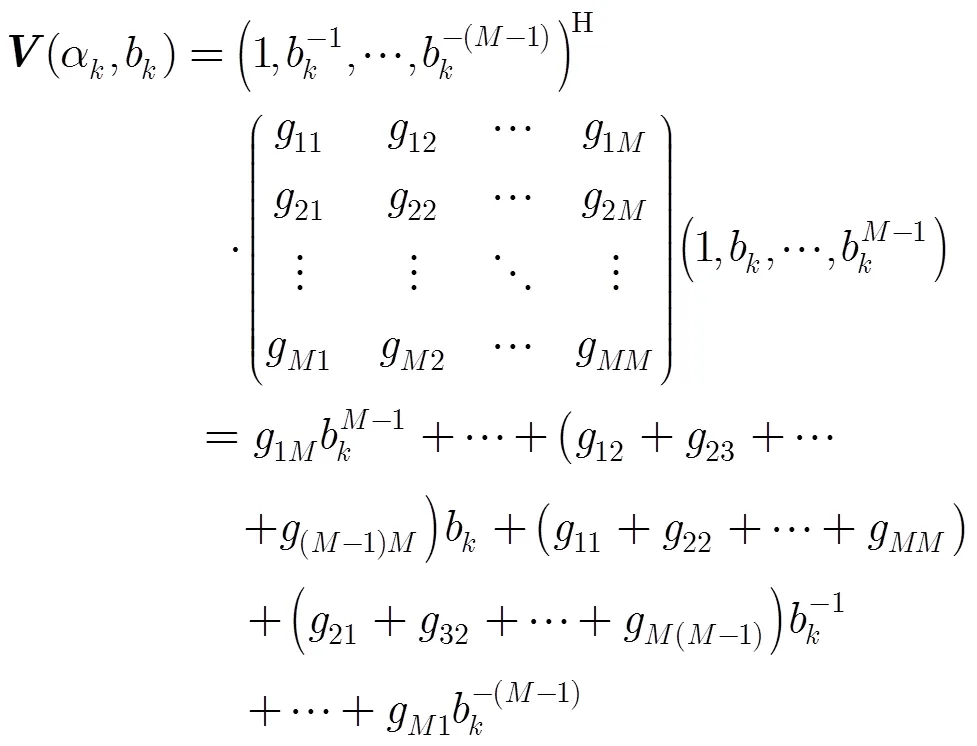
将式(16)代入式(15)得

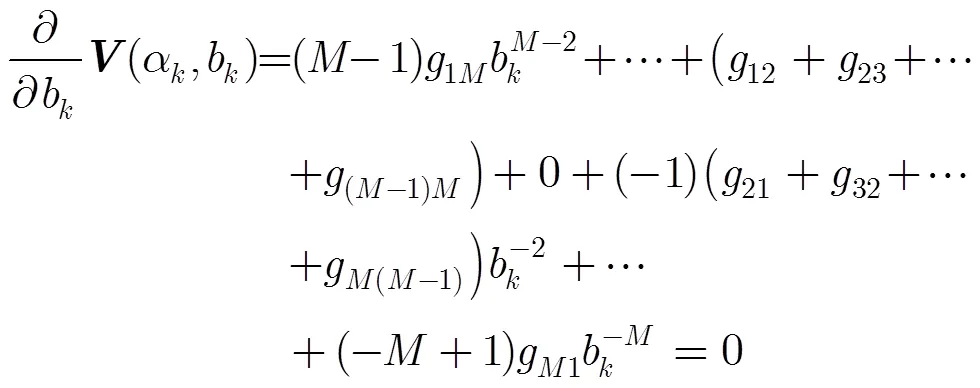
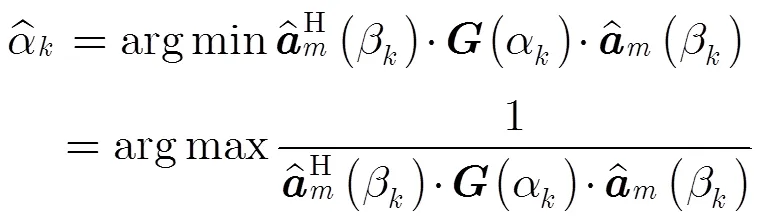
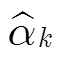
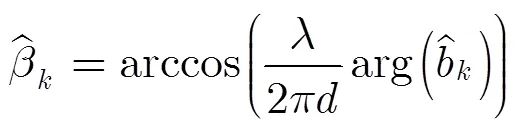
综上所述，MRD-MUSIC算法的步骤可以总结为：

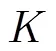
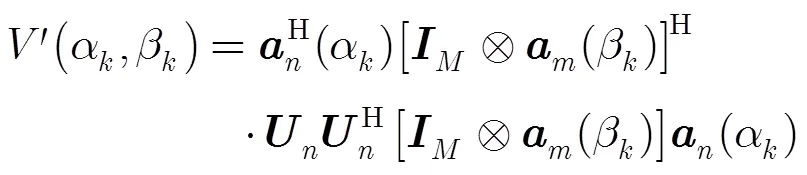
后续求解方法同前。

5 降维算法运算量

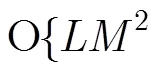
6 仿真分析

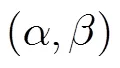
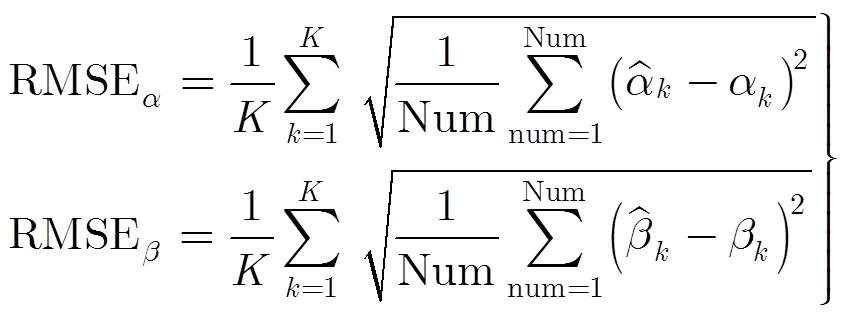
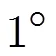
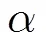
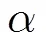
仿真实验表明，MRD-MUSIC算法的成功率始终远高于原RD-MUSIC算法的成功率，接近于2D-MUSIC算法的成功率。

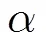
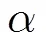
仿真实验表明，MRD-MUSIC算法的角度估计精度总是明显高于RD-MUSIC算法的角度估计精度，接近于2D-MUSIC算法的角度估计精度。

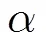
仿真实验表明，MRD-MUSIC算法的角度分辨率总是明显高于RD-MUSIC算法的角度分辨率，接近于2D-MUSIC算法的角度分辨率。

通过以上实验可知，本文提出的MRD-MUSIC算法角度估计的成功率、精确度和分辨率均优于RD-MUSIC算法，接近于2D-MUSIC算法的角度估计性能。

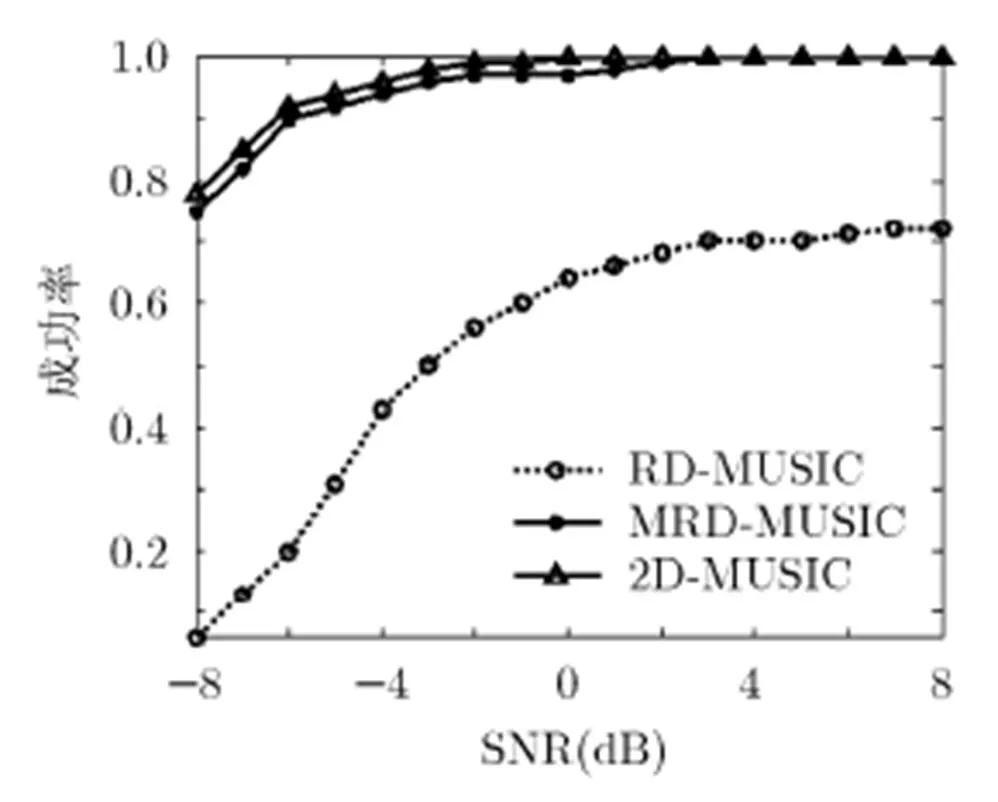
图2 角成功率随信噪比SNR变化曲线

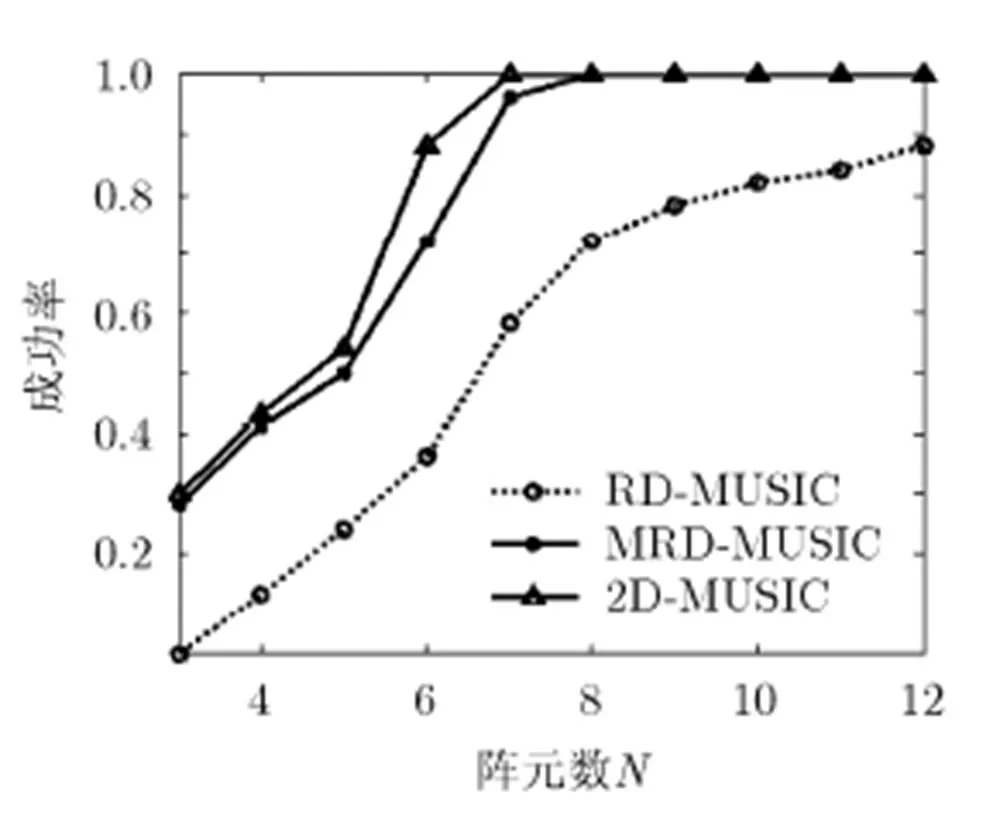
图3 角成功率随x轴阵元数N变化曲线

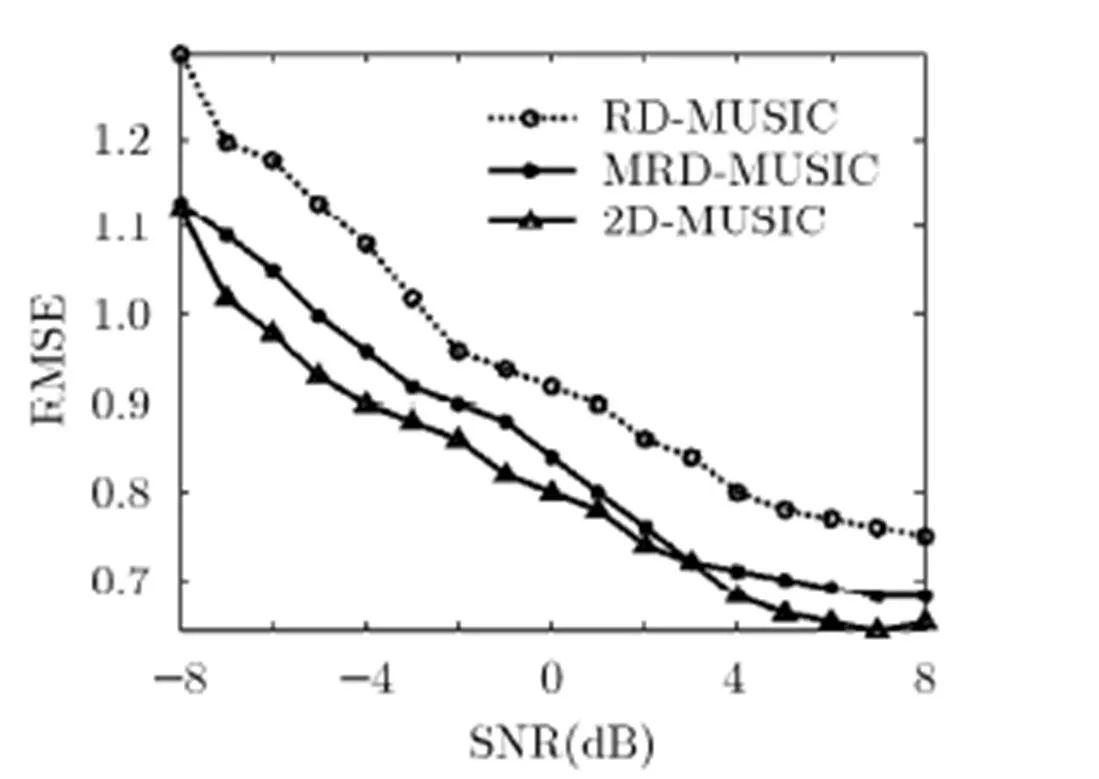
图4 角RMSE随SNR变化曲线

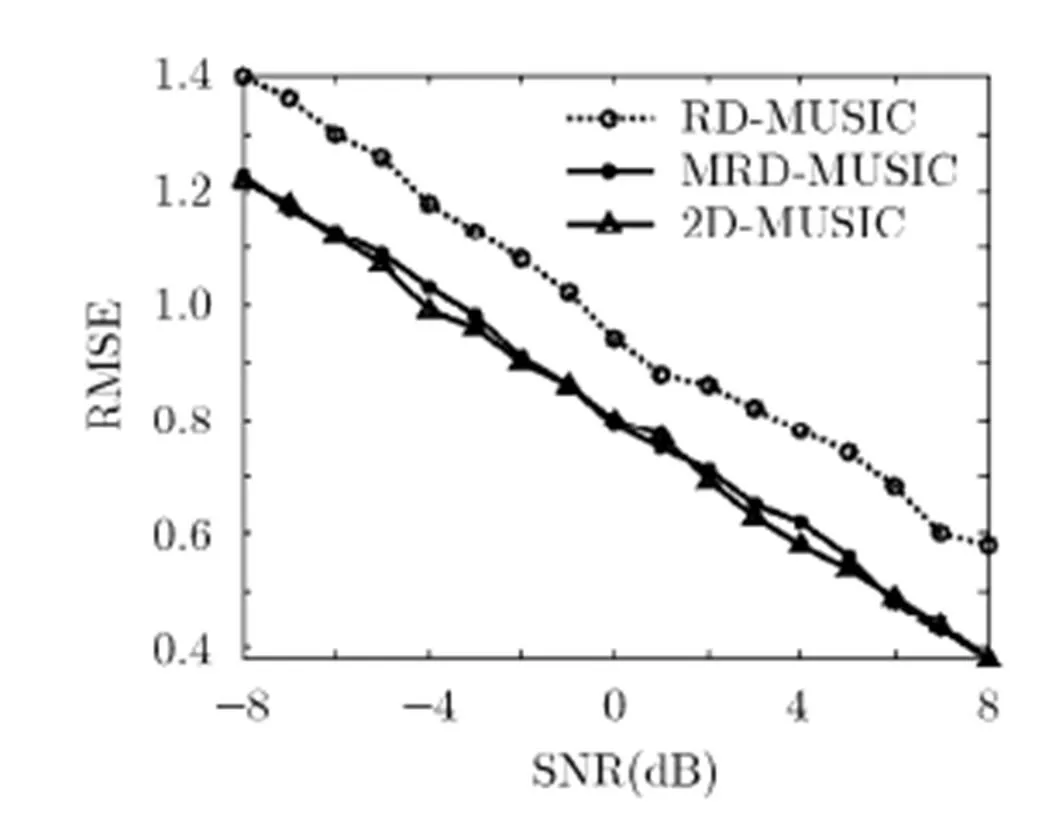
图5 角RMSE随SNR变化曲线

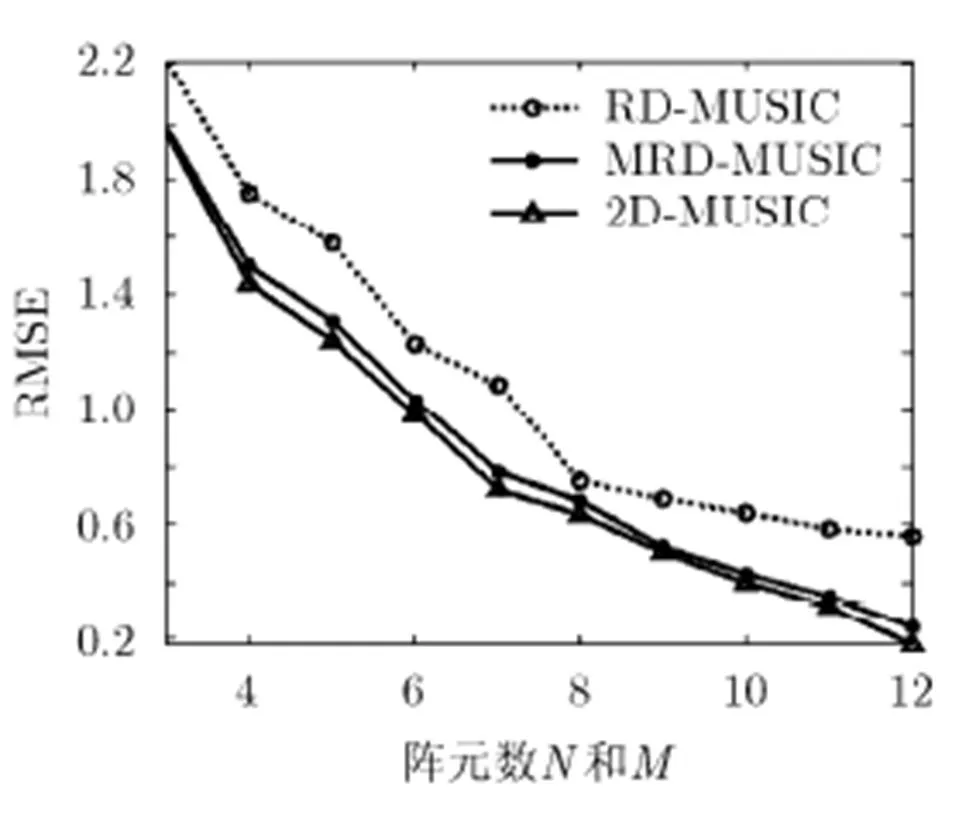
图6 角RMSE随N和M变化曲线

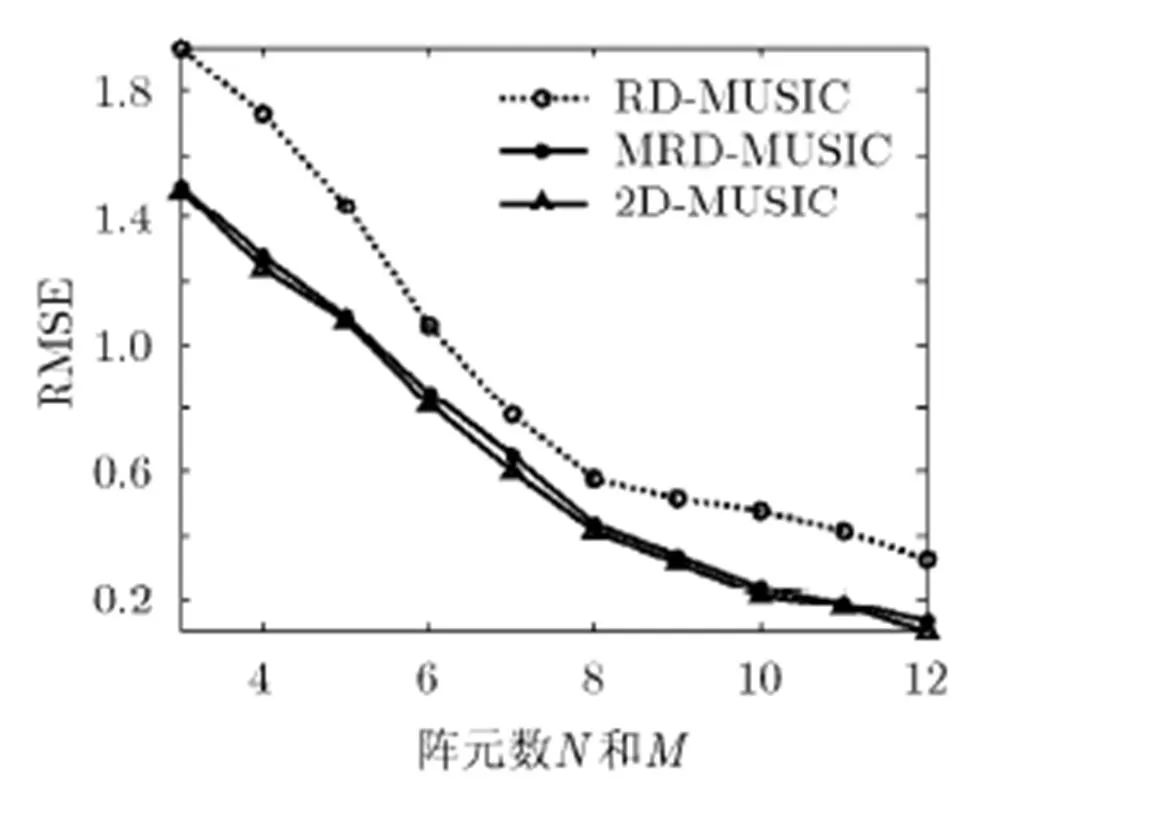
图7 角RMSE随N和M变化曲线

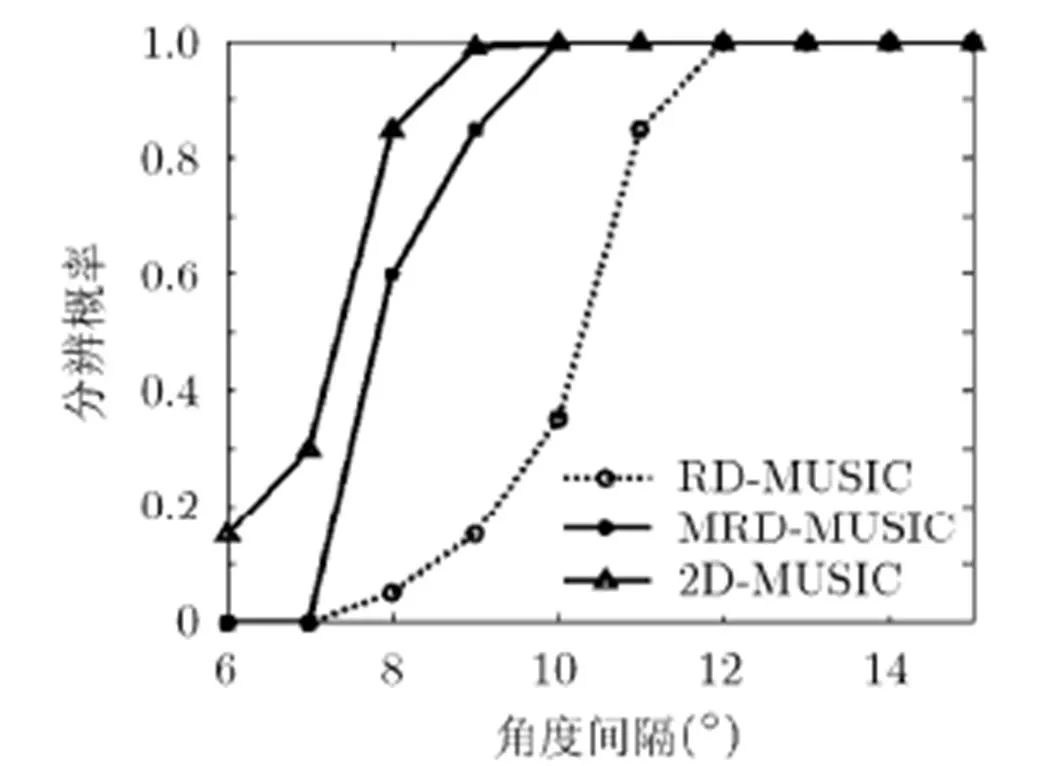
图8 角分辨概率随角度间隔变化曲线

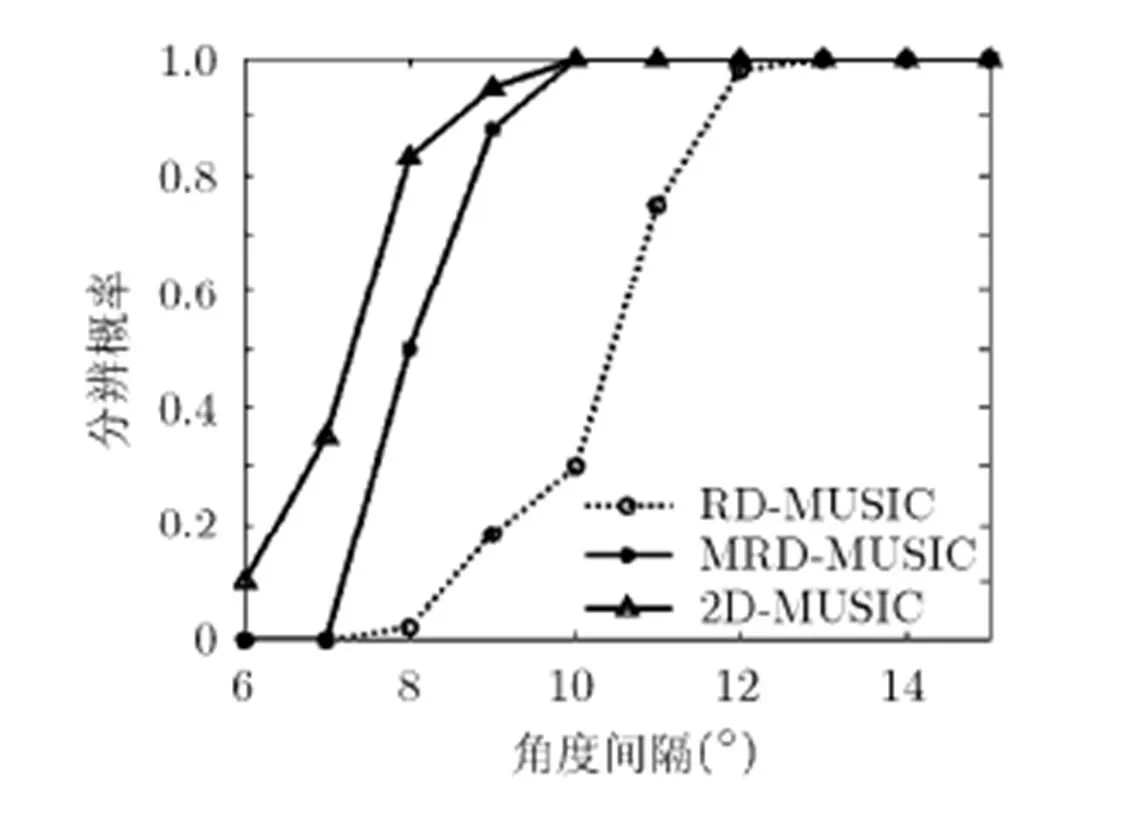
图9 角分辨概率随角度间隔变化曲线

7 结论

[1] Belouchrani A and Amin M G. Time-frequency MUSIC[J]., 1999, 6(5): 109-110.

[2] Chandran S and Ibrahim K. DOA estimation of wide-band signals based on time-frequency analysis[J]., 1999, 24(1): 116-121.

[3] 陈金立, 李家强, 顾红. 双基地MIMO雷达高速运动目标的DOD和DOA联合估计[J]. 电子与信息学报, 2013, 35(4): 859-864.

Chen Jin-li, Li Jia-qiang, and Gu Hong. Joint DOD and DOA estimation of high speed moving target in bistatic MIMO radar[J].&, 2013, 35(4): 859-864.

[4] Liang Jun-li and Liu Ding. Joint elevation and azimuth direction finding using L-shaped array[J]., 2010, 58(6): 2136-2141.

[5] 蔡晶晶, 李鹏, 赵国庆. RD-MUSIC的二维DOA估计方法[J]. 西安电子科技大学学报(自然科学版), 2013, 40(3): 81-86.

Cai Jing-jing, Li Peng, and Zhao Guo-qing. Two-dimensional DOA estimation with reduced-dimension MUSIC[J]., 2013, 40(3): 81-86.

[6] Hung C J and Chen C H. New algorithm for fast direction-of-arrival estimation using the shrinking signal subspace and the noise pseudo-eigenvector[J].,&, 2010, 4(4): 604-610.

[7] Bu Hong-wang, Hon Tat-hui, Mook Seng-leong. Decoupled 2D direction of arrival estimation using compact uniform circular arrays in the presence of elevation-dependent mutual coupling[J]., 2010, 58(3): 747-755.

[8] Zhang Y, Ye Z, Xu X,. Estimation of two-dimensional direction-of-arrival for uncorrelated and coherent signals with low complexity[J].&, 2010, 4(4): 507-519.

[9] Zhang X and Xu D. Angle estimation in MIMO radar using reduced-dimension Capon[J]., 2010, 46(12): 860-861.

[10] 许建忠, 孙红伟, 孙业岐, 等. 采用Radon-Wigner变换的二维波达方向估计[J]. 电子与信息学报, 2012, 34(4): 997-1001.

Xu Jian-zhong, Sun Hong-wei, Sun Ye-qi,. 2-D direction of arrival estimation method using Radon-Wigner transform[J].&, 2012, 34(4): 997-1001.

[11] Gu Jian-feng, Wei Ping, Tai Heng-ming. DOA estimation using cross-correlation matrix[C]. IEEE International Symposium on PhasedArray Systems and Technology (ARRAY), Boston, USA, 2010: 593-598.

[12] Weng Xiao-jun, Zhang Min, and Li Peng-fei. A new 2D-DOA estimation approach based on dimension-degraded model[C]. The 2nd International Conference on Information Science and Engineering(ICISE), Hangzhou, China, 2010: 4285-4288.

[13] Zhang X, Huang Y, Chen C,. Reduced-complexity Capon for direction of arrival estimation in a monostatic multiple-input multiple-output radar[J].&, 2012, 6(8): 796-801.

[14] 闫锋刚, 刘帅, 金铭, 等. 基于降维噪声子空间的二维阵列DOA估计算法[J]. 电子与信息学报, 2012, 34(4): 832-837.

Yan Feng-gang, Liu Shuai, Jin Ming,. 2-D DOA estimation method based on dimension descended noise subspace[J].&, 2012, 34(4): 832-837.

[15] 王凌, 李国林, 谢鑫, 等. 非圆信号二维DOA和初始相位联合估计方法[J]. 雷达学报, 2012, 1(1): 43-49.

Wang Ling, Li Guo-lin, Xie Xin,.. Joint 2-D DOA and noncircularity phase estimation method[J]., 2012, 1(1): 43-49.

[16] Zhang Xiao-fei, Xu Ling-yun, Xu Lei,. Direction Of Departure (DOD) and Direction Of Arrival (DOA) estimation in MIMO radar with reduced-dimension MUSIC [J]., 2010, 14(12): 1161-1163.

蔡晶晶： 女，1981年生，博士生，研究方向为阵列信号处理.

鲍 丹： 男，1975年生，副教授，研究方向为通信对抗技术等.

李 鹏： 男，1965年生，教授，研究方向为电子信息对抗技术等.

赵国庆： 男，1953年生，教授，博士生导师，研究方向为电子信息对抗技术等.

Two-dimensional DOA Estimation UsingReduced-dimensional MUSIC Algorithm with Strong-constraint Optimization

Cai Jing-jing Bao Dan Li Peng Zhao Guo-qing

(,,,710071,)

This paper proposes a Modified Reduced-Dimensional MUSIC (MRD-MUSIC) Direction Of Arrival (DOA) estimation algorithm to solve the computation-intensive problem in the two-dimensional DOA estimations. The MRD-MUSIC algorithm can distinctly reduce the computational load, since the two-dimensional DOA estimation can be decomposed into two stages of one-dimensional DOA estimations by the quadratic optimization method. In this algorithm, a one-dimensional DOA is obtained by the direct derivation of the quadratic optimization function, and the steering vectors are strongly constrained in the solving process, as a result, the derivation is closer to the optimal solution than the other’s. The simulation results verify that the theoretical derivations of this algorithm is of correctness, it does not need pair matching processes, and it has higher successful rate and precision of the angle estimation.

Two-dimensional Direction Of Arrival (DOA) estimation; Reduced-Dimensional MUSIC (RD-MUSIC); Optimization algorithm

TN911.7

A

1009-5896(2014)05-1113-06

10.3724/SP.J.1146.2013.01127

蔡晶晶 jjcai@mail.xidian.edu.cn

2013-07-30收到，2014-01-22改回

国家自然科学基金(61271300, 61072107)和中央高校基本科研业务费专项资金(K5051202003)资助课题