复杂噪声环境下基于LVD的LFM信号参数估计

2014-05-30段鹏婷姬红兵

电子与信息学报 2014年5期

关键词：低阶时频参数估计

金艳段鹏婷姬红兵

金艳段鹏婷*姬红兵

(西安电子科技大学电子工程学院西安 710071)

线性调频信号；LVD(LV’s Distribution)；分数低阶矩；参数估计；脉冲噪声

1 引言

线性调频(Linear Frequency Modulation, LFM)信号广泛应用于雷达、声呐、地质探测与生物医学等系统，是一类典型的非平稳信号。中心频率和调频斜率是表征LFM信号频率特性的基本参数，因而这两个参数的估计问题一直是信号处理领域的研究热点[1,2]。到目前为止，国内外学者提出了多种有效的处理方法。其中，基于极大似然(ML)估计的方法估计精度高，其误差估计曲线逼近CRLB界，但该方法需要对非线性代价函数进行优化，计算复杂度高，且可能收敛到局部极值点。以Wigner-Ville分布(WVD)[3]为代表的双线性时频分析方法，虽然在分析单分量LFM信号时可获得良好的能量聚集性，但对于多分量信号，这类非线性时频分布存在严重的交叉项。分量之间的交叉项会使时频平面变得模糊不清，不利于信号时频特性的准确提取，特别是在信噪比较低的场合，各LFM信号分量更难于分辨。使用核函数可对交叉项起到平滑抑制作用[4]，但同时牺牲了时频聚集性，而聚集性的下降又会导致相距较近分量间的可分辨性变差。短时傅里叶变换(STFT)和分数阶傅里叶变换(FrFT)属于线性变换，虽然二者均能避免交叉项的干扰，但STFT的估计效果在低信噪比条件下并不理想[5]，而FrFT由于要进行2维搜索，运算量大大增加[6]。

针对上述问题，本文结合相位尺度变换消除了信号自相关项在中心频率—调频斜率(CFCR)域的线性频率迁移，分析了多分量LFM信号的LVD(LV’s Distribution)表达式[7]能量高度聚集的特性。仿真结果表明对于高斯白噪声背景下的信号，LVD在低信噪比情况下能精确估计信号参数。另外，针对LVD在实际噪声具有显著脉冲特性时[8,9]性能严重恶化的问题，本文结合分数低阶统计量理论，提出了分数低阶LVD(FLOLVD)，该方法实现了脉冲噪声环境中LFM信号的参数估计。

2 LVD方法原理

多分量LFM信号的数学模型定义如下：

对于LFM信号，通常利用时频分析方法进行瞬时成像。如WVD在时频平面上具有很好的时频聚集性，表现为背鳍状，直线型。Hough变换用于检测和估计平面的直线，因而常将Hough变换与WVD结合起来(即WHT)对LFM信号的相位参数进行估计[10,11]。WHT的表达式为

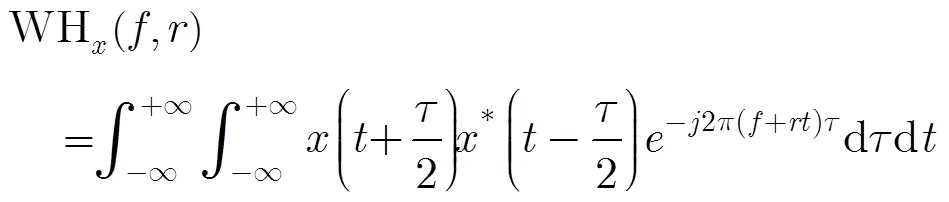
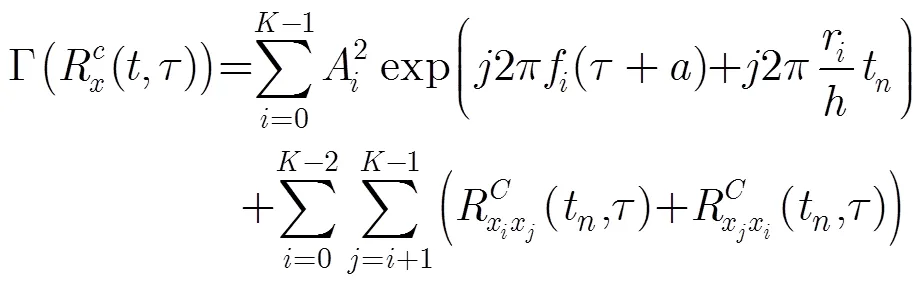
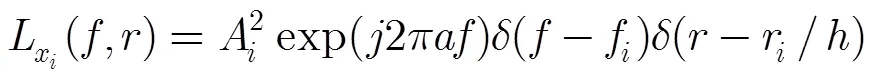
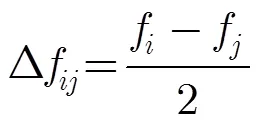
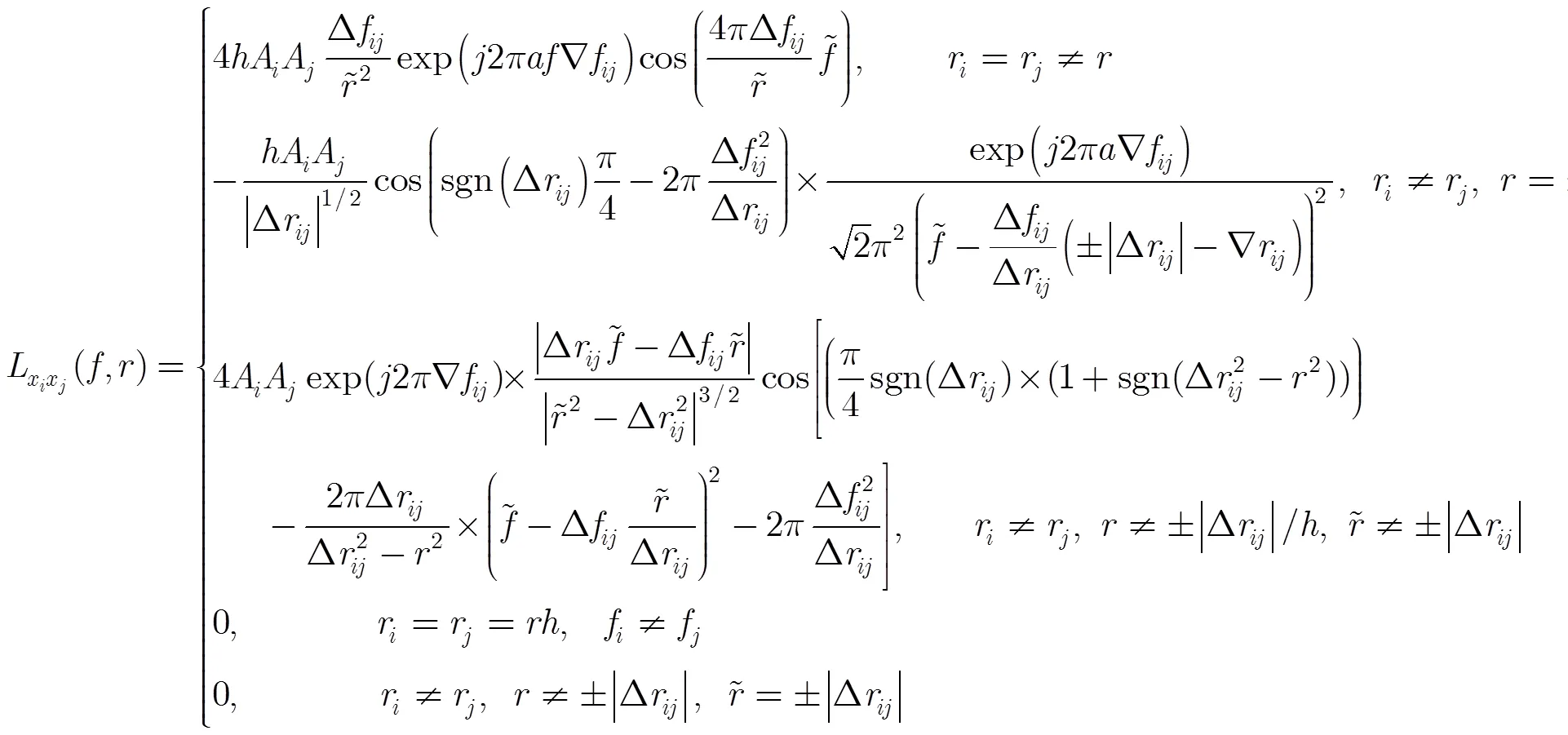
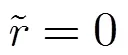
3 分数低阶LVD(FLOLVD)

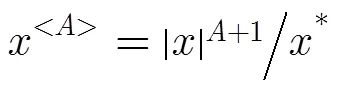
在基于二阶统计量的LFM信号参数估计算法中，脉冲噪声会形成较强的奇异值干扰，从而严重影响有用信号的时频特征提取。为此，可采用分数低阶理论抑制脉冲噪声。本文采用分数低阶算子对LVD方法中的PSIAF进行改进，

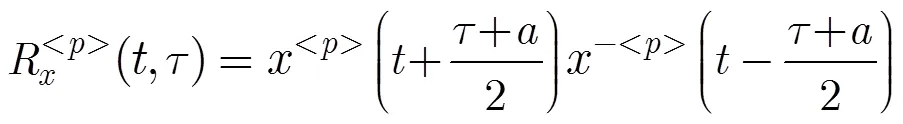
同理，将分数低阶算子推广到WHT，得到分数低阶WHT(FLOWHT)：

4 仿真结果及分析

4.1 估计性能比较

理论分析得知在无噪声干扰背景下，LVD可以对多分量LFM信号参数进行较高精度的参数估计。图1给出了无噪声情况下3分量LFM信号的WVD, WHT及LVD结果。

由图1(a)可知，WVD的聚集性良好，3条直线分别代表LFM信号的3个分量，但WVD平面还存在较为明显的具有振荡结构的交叉项。图1(b)为3分量LFM信号的WHT，其中Hough变换在时频平面沿直线方向对WVD作积分运算，其聚焦作用可抑制多分量LFM信号WVD中的交叉项。如图1(c)所示，LVD描述相同的LFM信号时，信号自项在CFCR域清晰明确，交叉项相对于信号自项幅值较小，可以忽略其影响，仿真结果与理论分析一致，验证了LVD方法的合理性和有效性。

图1 3分量LFM信号的WVD, WHT及LVD

图2 -3.dB高斯白噪声下3分量LFM信号的WHT和LVD

图2(a)为信号的WHT，由该图可以看出交叉项和噪声的干扰比较严重，两个平行且相距较近的LFM信号的交叉项经Hough变换后形成伪尖峰，在低阈值下会造成误检测。由图2(b)可知，LVD在CFCR域有效抑制了高斯噪声，可精确估计LFM信号各分量的中心频率和调频斜率，相应的参数估计值如表1所示。

图3(a)中，脉冲噪声环境下LFM信号的FLOWHT伪峰较多，因而信号自项的特征参数难以准确提取。图3(b)中，信号项周围的起伏为噪声和交叉项的贡献，相对于信号自项这部分能量分散；由该图可知信号自项在CFCR域呈现较高的能量聚集，有利于实现信号项的参数估计。但是与图2(b)相比幅值下降，这是因为分数低阶算子对LFM信号幅度产生了抑制作用。

表1和表2分别给出了高斯噪声和脉冲噪声情况下，经过100次Monte-Carlo实验所得的中心频率和调频斜率估计值的算术平均值。

表1和表2表明，本文LVD及其改进算法的估计误差明显低于WHT及FLOWHT，所得到的相位参数估计值更接近于真实值，有效地提高了参数估计精度。此外，如图2和图3所示，WHT及FLOWHT的交叉项干扰严重，平滑交叉项虽可抑制伪尖峰，但也降低了时频聚集性，使Hough变换后尖峰幅度降低和参数估计的精度下降，同时也增加了Hough变换的运算复杂度。本文方法在时频分辨率较高的情况下，具有较好的交叉项抑制效果。综上可知，本文方法估计性能明显优于WHT及FLOWHT。

图3 -3.dB脉冲噪声环境下3分量LFM信号的FLOWHT和FLOLVD

表1 -3 dB白噪声中多分量LFM信号相位参数估计值和实际值

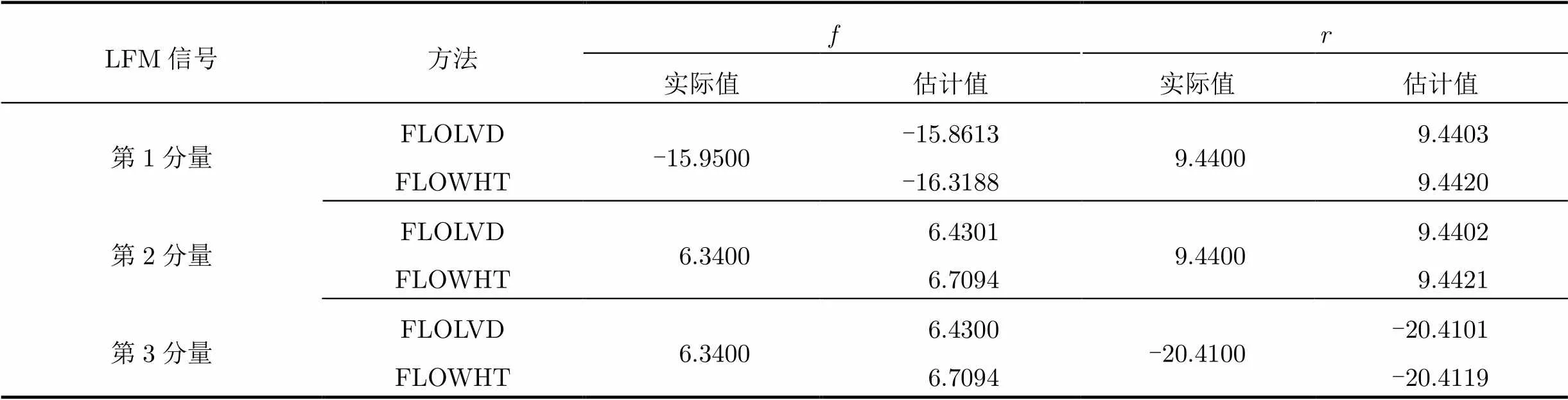
表2 -3dB脉冲噪声中多分量LFM信号相位参数估计值和实际值

4.2 噪声抑制结果及分析

5 结束语

针对LFM信号的参数估计问题，本文首先介绍了LVD，然后结合分数低阶理论，提出了适用于脉冲噪声的FLOLVD方法，给出了算法步骤。仿真实验表明，本文方法在复杂噪声背景下，实现了LFM信号中心频率和调频斜率的估计，并具有较好的估计性能。与常规方法相比，本文方法克服了交叉项的影响，并且利用该方法能量高度聚集的特性，提高了参数空间的分辨率，同时获得了较高的估计精度。

图4 高斯白噪声下信号的分布聚集比

图5 脉冲噪声下信号的分布聚集比

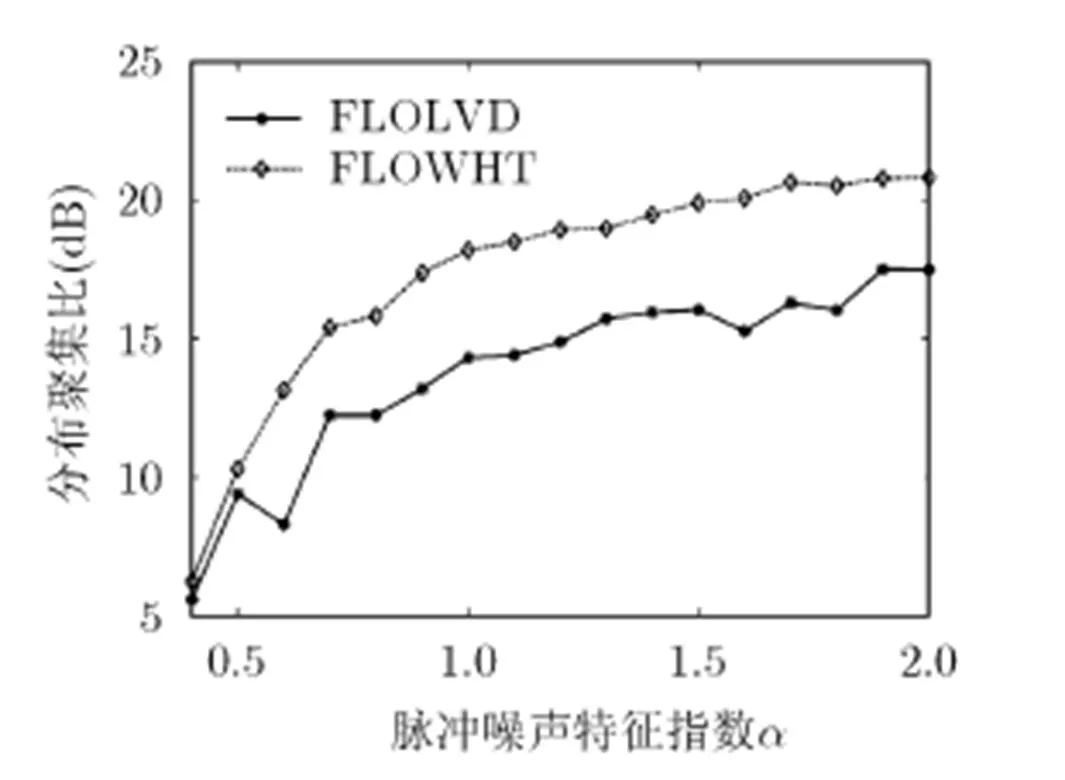
图6 分布聚集比随的变化曲线

[1] Bi G A, Li X M, and Samson S C M. LFM signal detection using LPP-Hough transform[J]., 2011, 91(6): 1432-1443.

[2] 金艳, 姬红兵. 一种基于循环平稳的Chirp信号相位参数估计迭代算法[J]. 电子与信息学报, 2008, 30(4): 868-871.

Jin Yan and Ji Hong-bing. A cyclostationarity based iterative algorithm for chirp signal phase parameter estimation[J].&, 2008, 30(4): 868-871.

[3] Arce G R and Hasan S R. Elimination of interference terms of the discrete Wigner distribution using nonlinear filtering[J]., 2000, 48(8): 2321-2331.

[4] Thomas M, Lethakumary B, and Jacob R. Performance comparison of multi-component signals using WVD and Cohen’s class variants[C]. IEEE 2012 International Conference on Computing, Electronics and Electrical Technologies (ICCEET), Kumaracoil, 2012: 717-722.

[5] Pei S C and Huang S G. STFT with adaptive window width based on the chirp rate[J].,2012, 60(8): 4065-4080.

[6] 李家强, 金荣洪, 耿军平, 等. 基于高斯短时分数阶傅里叶变换的多分量LFM信号检测与参数估计[J]. 电子与信息学报, 2007, 29(3): 570-573.

Li Jia-qiang, Jin Rong-hong, Geng Jun-ping,.. Detection and estimation of multi-component LFM signals based on Gauss short-time fractional Fourier transform[J].&, 2007, 29(3): 570-573.

[7] Lv X L, Bi G A, Wan C R,.. Lv’s distribution: principle, implementation, properties, and performance[J]., 2011, 59(8): 3576-3591.

[8] Li L, Qiu T, and Song D. Parameter estimation based on fractional power spectrum under alpha-stable distribution noise environment in wideband bistatic MIMO radar system[J]., 2013, 67: 947-954.

[9] Nikias C L and Shao M. Signal Processing with Alpha-stable Distribution and Application[M]. New York: John Wiley & Sons1995: 126-158.

[10] Song Y, Hu J, and Xu J S. Motion compensation based on Keystone transform and Wigner-Hough transform[J]., 2012, 220: 2208-2212.

[11] Gulum T O, Erdogan A Y, Yildirim T,. Parameter extraction of FMCW modulated radar signals using Wigner-Hough transform[C]. 2011 IEEE 12th International Symposium on Computational Intelligence and Informatics (CINTI), Budapest, 2011: 465-468.

[12] Zhu D, Li Y, and Zhu Z. A keystone transform without interpolation for SAR ground moving-target imaging[J]., 2007, 4(1):18-22.

[13] Xing M, Lan J,Bao Z,.. ISAR echoes coherent processing and imaging[C]. 2004 IEEE Aerospace Conference,Montana, 2004, 3:1946-1960.

[14] 黄翀鹏, 王剑, 徐保国. 旁瓣抑制对线性调频脉冲移频干扰的影响[J]. 雷达学报, 2012, 1(3): 270-276.

Huang Chong-peng, Wang Jian, and Xu Bao-guo. The impact of sidelobe suppression in shift-frequency jamming against LFM[J]., 2012, 1(3): 270-276.

[15] 杨利民, 苏卫民, 顾红, 等. 基于二维映射的 LFMUWB 雷达动目标速度估计[J]. 雷达学报, 2012, 1(3): 232-237.

Yang Li-min, Su Wei-min, Gu Hong,.. Velocity estimation of moving target based on two-dimensional projection for LFMUWB radar[J]., 2012, 1(3): 232-237.

[16] Liu W. Time delay estimation for low SNR signals with impulsive noises using fractional low order covariation sequences[C]. IEEE 2012 International Conference on Audio, Language and Image Processing (ICALIP), Shanghai, 2012: 647-650.

[17] Ma X Y and Nikias C L. Joint estimation of time delay and frequency delay in impulsive noise using fractional lower order statistics[J]., 1996, 44(11): 2669-2687.

[18] Li X M, Bi G A, Stankovic S,.. Local polynomial Fourier transform: a review on recent developments and applications[J]., 2011, 91(6): 1370-1393.

金艳：女，1978年生，博士，副教授，硕士生导师，主要研究方向为现代信号处理、统计信号处理、信号检测与估计、通信信号侦测等.

段鹏婷：女，1989年生，硕士生，研究方向为信号检测与估计、通信信号侦测.

姬红兵：男，1963年生，博士，教授，博士生导师，主要研究方向为光电信息处理、微弱信号检测与识别、医学影像处理等.

Parameter Estimation of LFM Signals Based on LVD in Complicated Noise Environments

Jin Yan Duan Peng-ting Ji Hong-bing

(,,710071,)

Linear Frequency Modulation(LFM) signal; LV’s Distribution (LVD); Fractional lower order moment; Parameter estimation; Impulsive noise

TN911.7

1009-5896(2014)05-1106-07

10.3724/SP.J.1146.2013.01013

段鹏婷 duanpt1206@163.com