基于振动信号的深沟球轴承滚动体故障诊断研究*

赵海峰 杨国斌

(东北石油大学机械科学与工程学院)

滚动轴承作为机械设备的重要旋转零件，是机械设备的重要故障源，据统计，旋转机械约30%的机械故障由滚动轴承引起，齿轮箱各类故障中的轴承故障率仅次于齿轮，占20%[1]，因此，滚动轴承的故障诊断一直是研究的重点，而深沟球轴承是滚动轴承中最为典型的一类轴承，在应用中量大面广[2]。

振动信号因具有丰富的滚动轴承运行状态信息、测试简便、相关理论较为成熟而得到广泛应用。但在实测振动数据分析过程中，仍然会遇到许多问题[3,4]。例如，目前针对滚动轴承内、外圈故障的研究较多，并且诊断效果较好，而关于滚动体故障的诊断研究很少；再者，如果仅以包络分析的谱图中显示的滚动轴承特征频率作为判断依据，会对故障部位出现误诊等。此外，目前Hilbert-Huang变换、小波分析及神经网络等方法虽然在滚动轴承的故障诊断研究中起到一定的积极作用，但这些方法对于现场技术人员而言是不容易理解和掌握的。针对上述这些问题，为了更清晰地与传统认知进行比较，笔者以美国凯斯西储大学(Case Western Reserve University)轴承数据中心提供的公开轴承振动测试数据为研究对象，采用传统简单有效的时域统计参数和Hilbert包络谱分析方法，从分析结果中获得了深沟球轴承滚动体故障难以诊断的原因，并提出了简单可行的解决方法。

1 时域统计参数计算

当滚动轴承发生局部故障时，轴承座处的振动测试数据的时域统计参数(有效值、峭度、脉冲因子与裕度因子)变化较为明显，这些参数在滚动轴承故障诊断中起着重要作用。同时，根据这些参数的大小可以判断滚动轴承的故障性质和损伤程度。

有效值XRMS、峭度K、脉冲因子I与裕度因子的C计算式分别为：

(1)

(2)

(3)

(4)

式中xi——采集得到的振动信号时间序列，i= 1，2，…,n。

2 深沟球轴承特征频率计算

当滚动轴承某元件出现局部损伤故障时，随着转轴旋转，损伤点与其他元件表面接触处将产生冲击脉冲力，激起轴承的高频固有振动，引发周期性的冲击脉冲衰减信号，并且冲击脉冲的周期间隔随损伤点出现位置的变化而变化[5,6]。为了确定深沟球轴承的故障发生部位，需要计算出相应的故障特征频率。通常深沟球轴承特征频率是其几何尺寸的函数，一般由外圈故障特征频率、内圈故障特征频率和滚动体故障特征频率确定。外圈故障特征频率fo、内圈故障特征频率fi和滚动体故障特征频率fb的计算式分别为：

(5)

(6)

(7)

式中DB——滚珠直径；

fr——内圈与外圈之间相对转速，单位rad/s；

n——滚动体个数；

p——节径；

β——接触角。

但是，需要注意的是，上述计算公式仅适用于滚动体纯滚动情况下的深沟球轴承。一般情况下，深沟球轴承的外圈固定，内圈随转轴转动，当内、外圈表面发生局部损伤时，滚动体形成的冲击脉冲激励是周期性的，所测振动信号的信噪比也比较高，因此目前传统方法和一些新的诊断方法均能有效诊断出这两种故障。但是，当滚动体表面出现局部损伤时，在深沟球轴承实际运行过程中，滚动体除了存在滚动现象之外，还可能存在滑动现象，并且滚动体的损伤点不能与内圈或外圈保持周期性接触，这样会导致反映滚动体故障的振动信号出现随机性，这也是目前诸多分析方法无法有效诊断出深沟球轴承滚动体故障的原因。

3 Hilbert包络谱分析原理

为了获取局部损伤故障时滚动轴承振动信号的特征频率信息，需要对振动信号进行包络解调分析。Hilbert包络解调是常用的包络分析技术之一。设一连续时间序列信号为x(t)，其Hilbert变换为：

(8)

则该信号的解析信号为：

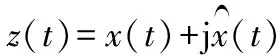
(9)

解析信号的幅值A(t)和相位Φ(t)的表达式为：

z(t)=A(t)ejΦ(t)

(10)

4 故障诊断实例

笔者所用分析数据来自于美国凯斯西储大学轴承数据中心，试验台的构成如图1所示。试验以电机驱动端SKF 6205-2RS深沟球轴承为研究对象，在轴承内、外圈和滚动体上均采用电火花技术设置直径为0.177 8、0.355 6、0.533 4mm 3种损伤程度的单点故障，其中外圈故障在负载区六点钟方向设置。为了比较不同转速和承载下的滚动轴承故障特征，在每种元件和损伤程度下设置1 730、1 750、1 772、1 797r/min共4种转速，所对应的承载分别为3、2、1、0HP。试验中采用电机驱动端垂直方向的加速度传感器采集振动信号，采样频率为12.00kHz。

图1 滚动轴承试验台

SKF6205-2RS深沟球轴承的规格参数如下：

内径 25.00mm

外径 52.00mm

厚度 15.00mm

滚珠直径 7.94mm

节径 39.04mm

滚动体数 9

接触角 0°

通过分析试验数据的时域统计参数可知，正常轴承、内圈故障和外圈故障的时域统计参数稳定，与转速和承载无关，这一结论与文献[1]中描述一致。但需注意的是，该结论仅在相同故障程度条件下成立，当损伤程度发生改变时，无量纲参数仍然会发生变化，如图2所示。

与前述3种状态相比，滚动轴承滚动体故障的时域统计参数无论故障程度相同与否，均出现了较大差异，存在明显的不确定性。笔者以损伤直径0.533 4mm为例，相同状况下正常与损伤状态下的统计参数见表1，与之相应的时域波形如图3、4所示。

图2 不同故障程度的时域统计参数

表1 滚动体故障时不同承载力情况下的时域统计参数

图3 滚动体正常时域波形

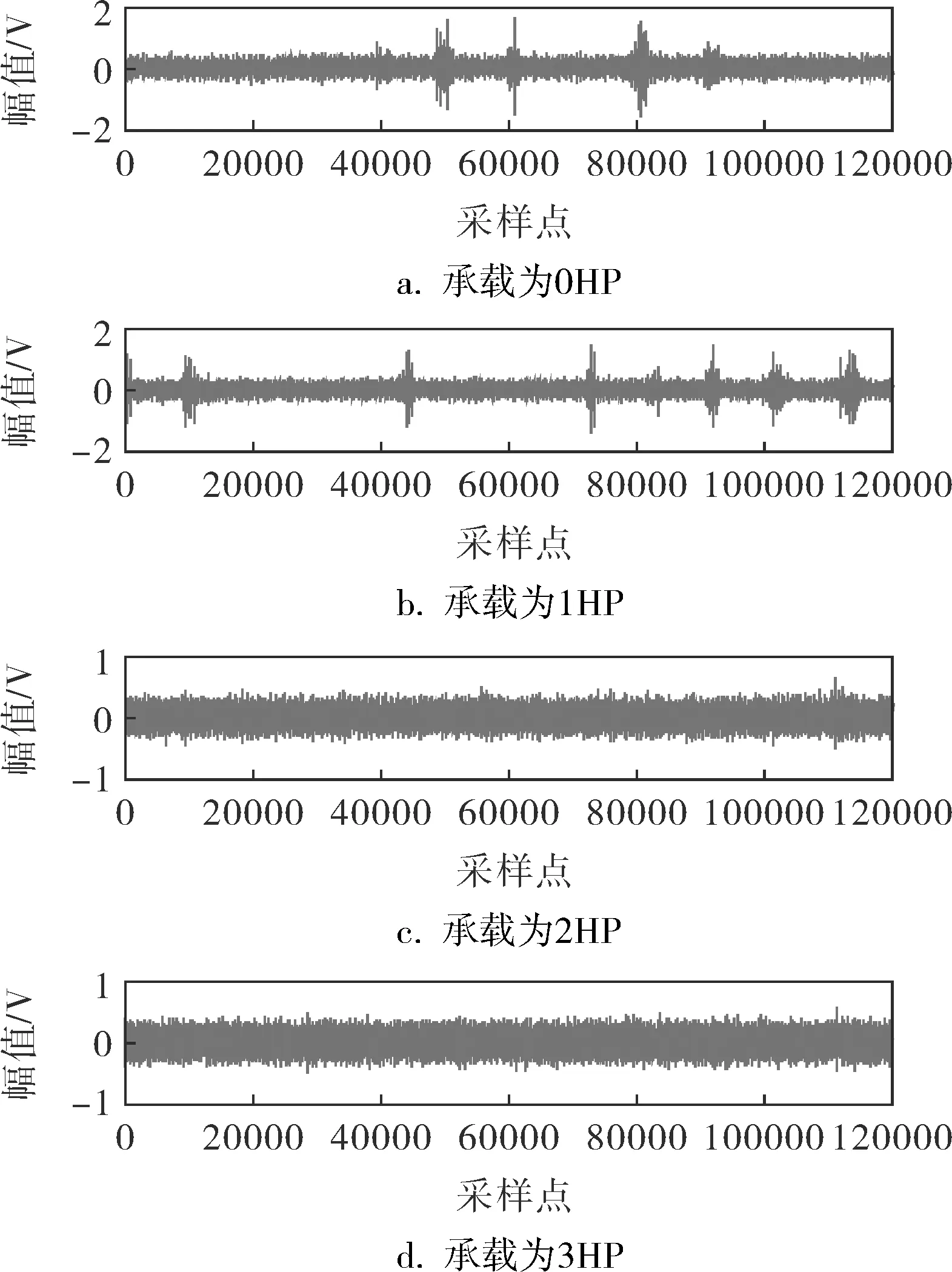
图4 滚动体故障时域波形

由图4可知，滚动体故障在4种承载能力下的时域波形图存在明显差异。图4a、b中出现了随机性的冲击信号，但图4c、d中几乎不存在这种情况。由表1可知，如果以采集的全部加速度数据段为分析数据，承载为0、1HP的时域统计参数与正常轴承相比出现了较大差异，尤其是峭度、脉冲因子与裕度因子反映了振动加速度信号中含有较大冲击信息，表明了该滚动轴承可能存在故障。但承载为2、3HP两种情况下采集的振动加速度数据的时域统计参数几乎与正常轴承一致，无法识别其故障。

图5所示为承载0HP时滚动体故障时域波形图，由如5可知，在明显冲击区域之外的时域波形(1～38 440点)与图4c、d非常相似，其时域统计参数也相近。当滚动体出现损伤故障时，可能导致滚动体与内、外圈滚道之间接触面处出现滑动状态，这种滑动将掩盖调制故障特征，测试得到的振动加速度信号中可能不存在反映滚动体故障特征频率的信息，而是近似于正常状态的信号，导致了诸多方法难以有效诊断出滚动体故障。因此，为了能够诊断出滚动体故障，应选取能够反映滚动体特征频率信息的脉冲测试信号时域波形进行分析。

图5 承载0HP时滚动体故障时域波形

以承载为0HP时的滚动体故障为例，依据前述滚动轴承特征频率计算公式，试验中，转速为1 797r/min情况下4种故障的特征频率为：

内圈故障 162.18Hz

外圈故障 107.36Hz

滚动体故障 141.17Hz

保持架 11.93Hz

图6是承载0HP时滚动体故障振动加速度信号的Hilbert包络谱，谱图中未显示滚动体故障的特征频率，而是较为清晰地显示了162.00Hz的内圈故障特征频率，如果据此判断该故障属于内圈故障，则会导致误诊。

图6 承载0HP时滚动体故障振动加速度信号的Hilbert包络谱

对图5中反映滚动体特征频率信息的区域1与区域2的脉冲数据段分别进行Hilbert包络谱分析，得到的Hilbert包络谱如图7所示。

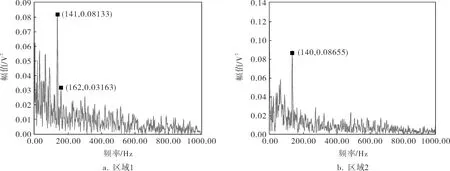
图7 滚动体特征频率信息脉冲数据段的Hilbert包络谱

图7清晰显示了与滚动体故障计算特征频率141.14Hz非常相近的在谱图中占主导成分的141.00、140.00Hz两个频率，由此可以判断该信号所描述的故障为滚动体故障。

5 结束语

滚动轴承典型的局部故障中，内、外圈故障诊断方法已经较为可靠，但滚动体故障诊断依然存在困难。通过对滚动轴承试验数据进行时域分析和Hilbert包络谱分析，确定了反映滚动体故障信息的振动加速度信号具有随机性，因此在进行滚动轴承故障诊断时，必须采集较长的振动加速度数据。如果时域波形中存在随机的脉冲数据段，则可以初步判断为滚动体故障，然后对该脉冲数据段利用Hilbert包络谱分析进行确诊。通过对滚动体故障振动加速度信号的包络解调分析可知，典型、单一局部故障的振动加速度包络谱中除含有相应的主导特征频率外，还可能存在幅值较小的其他几种故障特征频率，因此在该种情况下进行故障诊断时，应以主导特征频率对应的故障为判断依据，而不应确诊为混合故障。

[1] 李兴林，张仰平，曹茂来，等. 滚动轴承故障监测诊断技术应用进展[J]. 工程与试验, 2009, 49(4): 1～6.

[2] 杨晓蔚. 国内外深沟球轴承设计方法的对比[J]. 轴承，2010，(2)：59～61.

[3] 苏文胜, 王奉涛, 张志新, 等. EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]. 振动与冲击, 2010, 29(3): 18～21.

[4] 郭宝良, 段志善, 郑建校, 等. 振动机械滚动轴承单点点蚀故障诊断研究[J]. 振动工程学报, 2012, 25(5): 601～618.

[5] 唐贵基，蔡伟. 应用小波包和包络分析的滚动轴承故障诊断[J]. 振动、测试与诊断，2009，29(2)：201～204.

[6] 裴礼清, 张峰. 滚动轴承的滚动体与内圈接触部分的相对滑动分析[J]. 机械设计与研究，2000，(2): 53～55.