基于递推公式的星载SAR高效正向定位算法

李锦伟 李真芳 侯英龙 保 铮



基于递推公式的星载SAR高效正向定位算法

李锦伟*李真芳 侯英龙 保 铮

(西安电子科技大学雷达信号处理国防科技重点实验室 西安 710071)

该文提出一种基于递推公式的星载合成孔径雷达(SAR)高效正向定位算法。该算法利用3组递推公式计算待定位像素与参考像素之间的3轴位置增量，输入参数为两者之间的高程差、斜距差和方位时间差，然后将位置增量与参考点的位置相加即可求得待定位点的定位位置。3组递推公式通过分别以斜距、方位时间和高程为变量，并对定位方程组求导获取。该算法避免了3维格网建立、系数拟合和插值操作，仿真和实测数据定位结果验证了该文方法的精确性和有效性。

星载合成孔径雷达；定位；递推公式

1 引言

本文提出了一种基于递推公式的星载SAR高效正向定位算法。在SAR图像中选择2维格网，迭代获取格网像素的定位位置，然后利用3组递推公式和格网像素的定位位置求取待定位的非格网像素的定位位置，避免了3维格网建立、系数拟合和插值操作。本文结构如下：第2节介绍了本文算法的原理和处理流程，提出了一种改进的非格网像素高程获取方法；第3节通过仿真实验和实测数据处理验证了算法的精确性和有效性；最后总结全文。

2 算法原理

2.1 星载SAR定位模型

星载SAR常用如式(1)~式(3)所示的距离-多普勒模型进行目标定位[1,2]：

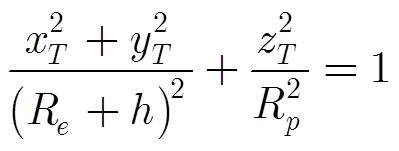
2.2 定位模型的求解

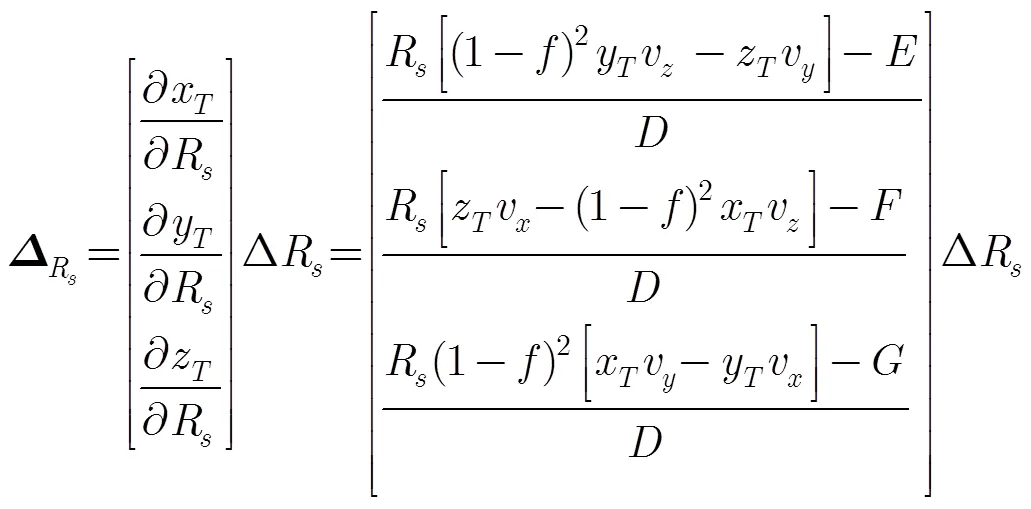
其中

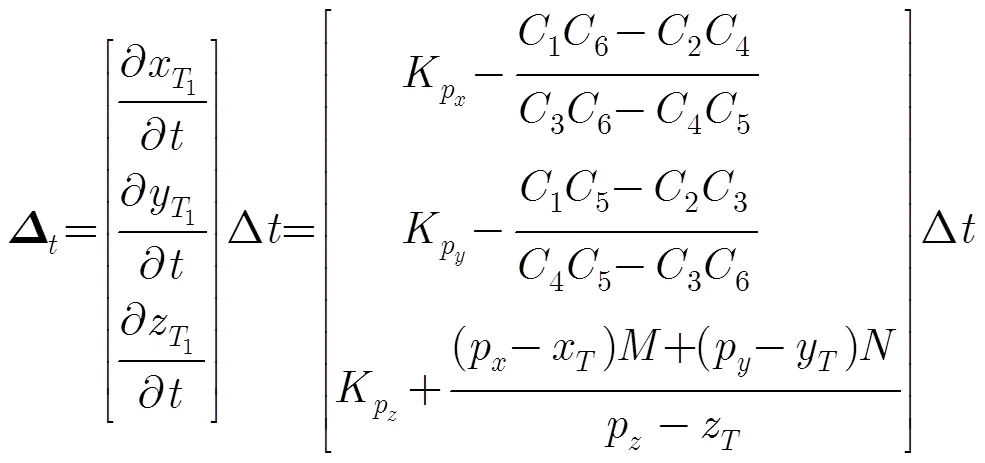
其中

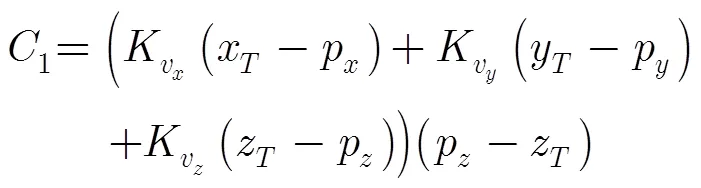
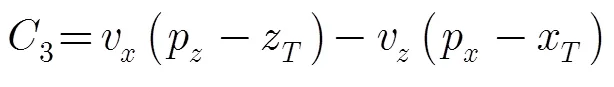
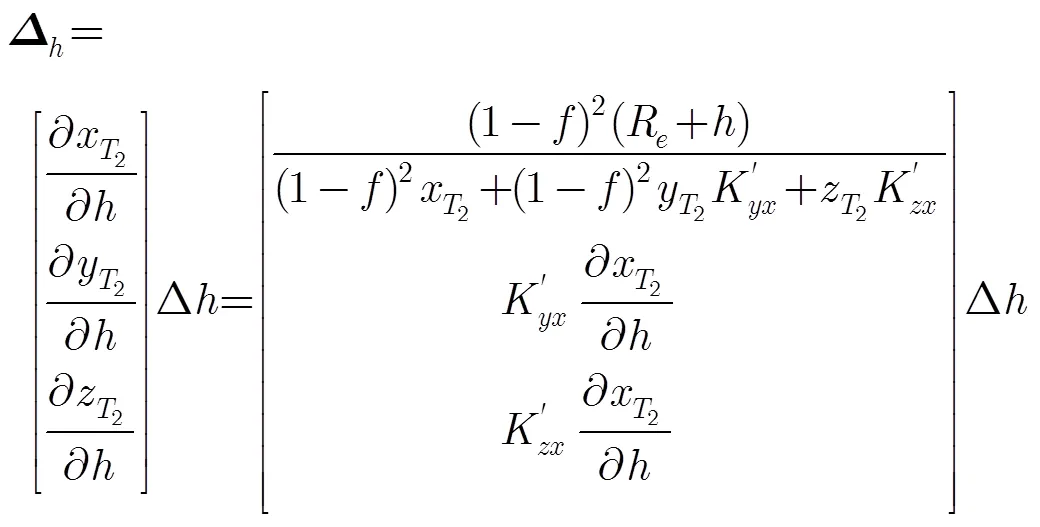
其中

为降低运算复杂度，仅用一阶导数来描述3轴位置增量与斜距差、方位时间差和高程差的关系，因为星载SAR的斜距较大[18]，在局部区域利用一阶导数表示的直线来近似斜距球、地球椭球及多普勒锥的曲线的精度已足够高，因此，仅用一阶导数描述是合理的。同样由于星载SAR的斜距较大，点目标位置随斜距、方位时间和高程的变化率在局部区域内近似恒定，待定位像素的3维位置可使用同一参考像素的递推系数来解算。

2.3 处理流程

本文定位方法的处理流程分为4步，如图2所示。

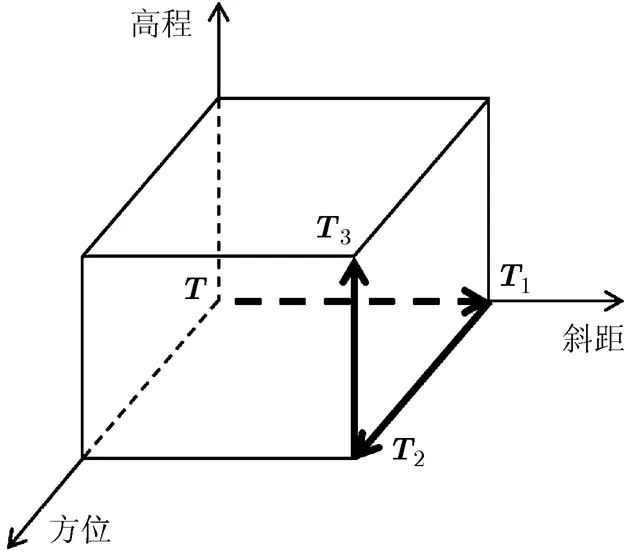
图1 待定位点3维位置的计算路径

图2 本文方法的处理流程

图3 迭代方法获取目标点位置和高程的流程图

(2)利用格网像素高程得到非格网像素的高程。

(3)根据式(4)-式(18)计算每个格网像素的递推系数。

(4)利用最近格网像素的递推系数计算非格网像素的3维定位位置，输入参数为待定位像素与参考格网像素之间的斜距差，方位时间差和高程差。

对于上述处理流程，如果定位前SAR图像像素高程已知，则直接跳过步骤(2)；对于定位前SAR图像像素高程未知的情况，需利用格网像素的高程得到每个像素的高程。根据式(19)可知，像素的高程误差直接导致定位误差，为降低非格网像素的高程误差，这里给出一种非格网像素高程获取方法：通过插值格网像素的经纬度得到非格网像素的经纬度，然后在DEM中取出相应位置的高程。

3 实验结果

本节进行仿真实验来验证递推公式的有效性，主要的系统参数取值见表1，卫星轨道参数分别来源于TerraSAR-X和Radarsat-2录取的SAR图像。

表1主要系统参数

参数采样频率(MHz)PRF(Hz)场景近边斜距 (s) 参数1109.883637.654.762216830 参数2 56.301600.226.563154014

与迭代方法定位结果相比，成像多普勒中心为0 Hz和2000 Hz时，利用递推公式求解待定位点位置的误差分别如图5(a)~图5(b)所示。由图5知，本文算法在不同成像多普勒中心下的定位精度几乎相同，待定位点与参考点之间的坐标增量小于50 m时，3轴定位误差小于0.02 m。

本文采用TerraSAR-X于2008年3月10日录取的美国大峡谷区域的部分SAR图像验证本文算法的性能。

图6(a)为TerraSAR-X录取的SAR图像，图6(b)为定位输入对应区域的SRTM(Shuttle Radar Topography Mission)DEM。选择格网像素间距为30像素，将迭代方法[11]获取的非格网像素的高程作为真值，通过插值得到非格网像素的经纬度，然后在DEM中取出相应高程的精度如表2和图7(a)所示。

表2本文非格网像素高程获取精度(m)

误差绝对值均值误差绝对值标准差最大正误差最大负误差 0.04095410.12389095.432824-4.096036

图6 算法验证所用美国大峡谷区域实测数据

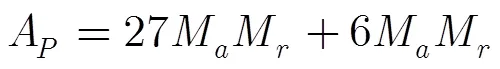
距离向和方位向格网间距都为30像素时，本文方法的定位误差如图7(b)-图7 (d)所示。算法实现语言为C++，基本运行环境为：Intel i3处理器，2.0 GB内存，本文方法和多项式方法的差异部分运行时间分别为0.078 s和1.547 s，可以看出，本文方法较多项式方法的运行时间大幅降低。

图7所示的定位误差中，既包括了利用递推公式或多项式拟合解算目标位置引入的误差，也包括图7(a)所示的待定位像素高程误差引入的定位误差。可以看出，在不包含待定位像素高程误差引入的定位误差，且格网像素间隔小于50 m时，本文算法的定位误差小于0.02 m，与仿真实验结果一致；包含像素高程误差引入的定位误差时，定位误差小于0.1 m。

4 结论

本文提出了一种基于递推公式的SAR高效正向定位算法。该算法利用3组递推公式计算待定位像素与参考像素之间的3轴位置增量，然后将计算出的位置增量与参考点的位置相加求得待定位点的3维位置，避免了3维格网建立、系数拟合和插值操作。仿真和实测数据的处理结果表明，本文算法具有较高的精度和较低的运算复杂度。

图7 文献[11]方法和本文方法的定位精度

[1] Curlander J C. Location of spaceborne SAR imagery[J]., 1982, 20(3): 359-364.

[2] 王青松, 黄海风, 董臻, 等. 星载合成孔径雷达高精度快速定位方法[J]. 科学通报, 2011, 56(11): 2609-2615.

Wang Qing-song, Huang Hai-feng, Dong Zhen,.. High- precision, fast geolocation method for spaceborne synthetic aperture radar[J]., 2011, 56(11): 2609-2615.

[3] Tao C V and Hu Y. A comprehensive study of the rational functional model for photogrammetric processing[J].&, 2001, 67(12): 1347-1357.

[4] Frey O, Santoro M, Werner C L,.. DEM-based SAR pixel-area estimation for enhanced geocoding refinement for enhanced geocoding refinement and radiometric normalization[J]., 2013, 10(1): 48-52.

[5] Pedlar D N and Coe D J. Target geolocation using SAR[J].,and, 2005, 152(1): 35-42.

[6] 史绪国, 张路, Balz T, 等. 一种用于SAR影像地理编码的改进的三维格网插值方法[J]. 武汉大学学报(信息科学版), 2012, 37(11): 1325-1331.

Shi Xu-guo, Zhang Lu, Balz T,.. A modified 3D grid interpolation method for satellite SAR geocoding[J]., 2012, 37(11): 1325-1331.

[7] 尹建凤, 李道京, 吴一戎. 顺轨三频三孔径星载SAR的运动目标检测及定位方法研究[J]. 电子与信息学报, 2010, 32(4): 902-907.

Yin Jian-feng, Li Dao-jing, and Wu Yi-rong. Research on the method of moving target detection and location with three-frequency three-aperture along-track spaceborne SAR[J].&, 2010, 32(4): 902-907.

[8] 燕英, 周荫清, 李春升, 等. 弹载合成孔径雷达成像处理及定位误差分析[J]. 电子与信息学报, 2002, 24(12): 1932-1938.

Yan Ying, Zhou Yin-qing, Li Chun-sheng,.. Missile- borne SAR imaging and error analysis of positioning[J].&, 2002, 24(12): 1932-1938.

[9] Sansosti E, Berardino P, Manunta M,.. Geometrical SAR image registration[J]., 2006, 44(10): 2861-2870.

[10] Nitti D O, Hanssen R F, Refice A,.. Impact of DEM- assisted coregistration on high resolution SAR interferometry [J]., 2011, 49(3): 1127-1143.

[11] Eineder M. Efficient simulation of SAR interferograms of large areas and of rugged terrain[J]., 2003, 41(6): 1415-1427.

[12] 郭交, 李真芳, 刘艳阳, 等. 基于粗数字高程模型信息的干涉相位图生成方法[J]. 电子与信息学报, 2010, 32(11): 2642-2647.

Guo Jiao, Li Zhen-feng, Liu Yan-yang,.. Approaches to interferogram generation based on coarse DEM[J].&, 2010, 32(11): 2642-2647.

[13] Walter D and Busch W. Influences of DEM quality parameters on the topographic phase correction in DInSAR [C]. International Geoscience & Remote Sensing Symposium 2012, Munich, Germany, July. 22-27, 2012: 3927-3930.

[14] Delft Institute of Earth Observation and Space Systems (DEOS), Delft object-oriented radar interferometric software user’s manual and technical documentation, Version v4.02, TUDelft Netherlands, 2008: 22-24.

[15] Prats P, Macedo A C, Reigber A,.. Comparison of topography-and aperture dependent motion compensation algorithms for airborne SAR[J]., 2007, 4(3): 349-353.

[16] Lachaise M, Balss U, Fritz T,.. The dual-baseline interferometric processing chain for the TanDEM-X mission[C]. International Geoscience & Remote Sensing Symposium, Munich, Germany, July. 22-27, 2012: 5562-5565.

[17] Lachaise M, Fritz T, Balss U,.. Phase unwrapping correction with dual-baseline data for the TanDEM-X mission[C]. International Geoscience & Remote Sensing Symposium, Munich, Germany, July. 22-27, 2012: 5566-5569.

[18] Cumming I G and Wong F H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M].Norwood,USA, Artech House, 2005: 113-168.

李锦伟： 男，1987年生，博士生，研究方向为星载合成孔径雷达系统设计与数据处理.

李真芳： 男，1977年生，教授，博士生导师，研究方向为合成孔径雷达干涉系统设计.

侯英龙： 男，1989年生，博士生，研究方向为机载合成孔径雷达运动补偿和干涉处理.

A Novel Efficient Spaceborne SAR Geolocation Method Based on Recursion Formulae

Li Jin-wei Li Zhen-fang Hou Ying-long Bao Zheng

(,,710071,)

A novel efficient geolocation method for spaceborne Synthetic Aperture Radar (SAR) is proposed based on recursion formulae in this paper. In this method, three groups of recursion formulae are utilized to compute the three-axis position increments between the position-unknown pixel and the adjacent position-determined pixel, i.e. the reference pixel, with the input increments of the height, slant range and azimuth time between the two pixels. Subsequently, these increments are added to the position of the reference pixel to obtain the position of the position-unknown pixel. Regarding respectively the height, slant range and azimuth time as the variables, these recursion formulae are acquired by differentiating the geolocation equations. Consequently, the construction of three-dimensional grid, coefficients fitting and interpolation are avoided in this method. The geolocation results of simulated and real data validate the accuracy and effectiveness of this method.

Spaceborne Synthetic Aperture Radar (SAR); Geolocation; Recursion formulae

TN959.74

A

1009-5896(2014)02-0409-06

10.3724/SP.J.1146.2013.00609

李锦伟 1jw2006147@sina.com

2013-05-03收到，2013-09-16改回

国家自然科学基金(41001282, 60802074, 40871205)和中央高校基本科研业务费(K5051302014)资助课题