线性调频信号主瓣不展宽旁瓣抑制方法

郭 瑞 蔡志明 姚直象



线性调频信号主瓣不展宽旁瓣抑制方法

郭 瑞*蔡志明 姚直象

(海军工程大学电子工程学院 武汉 430033)

以汉明窗为代表的加权方法在抑制线性调频信号的匹配滤波输出峰值旁瓣的同时展宽主瓣，致使距离分辨力下降。为兼顾旁瓣抑制和高距离分辨力的需求，该文提出一种新的主瓣不展宽旁瓣抑制方法。该方法首先将匹配滤波和加权处理的输出幅度进行归一化处理，然后逐点进行比较，再取各点对应的最小值作为最终的输出数据。该方法兼取了匹配滤波和加权处理的优点，其-3 dB主瓣展宽系数与匹配滤波相比仅为1，而旁瓣抑制性能和对应的加权处理相当。仿真结果和湖上试验验证了该方法的有效性。

信号处理；线性调频信号；旁瓣抑制；主瓣宽度；匹配滤波；汉明加权

1 引言

LFM的固有缺陷是通过匹配滤波器之后的输出有较高的距离旁瓣。在多目标环境中，强目标回波的输出旁瓣很可能混淆或者掩盖弱目标回波的主峰，影响对弱目标的探测和分辨。为了提高分辨多目标的能力，必须采用旁瓣抑制或简称加权技术[12,13]。加权可以在发射端，接收端或收、发两端上进行，为了保持系统的发射效率，通常在匹配滤波器输出之后采用频域幅度加权。

常规加权处理在降低旁瓣的同时，输出主瓣有不同程度的展宽，造成距离分辨力下降[14]。在多亮点目标的要害部位定位、目标精确成像、多目标分辨等应用场合中，对距离分辨力要求苛刻。为了兼顾旁瓣抑制和高距离分辨力需求，本文提出了一种新的主瓣不展宽旁瓣抑制方法。该方法对于距离分辨力要求苛刻场合下的多目标分辨、定位和识别具有重要应用价值。

2 LFM的常规加权方法性能

LFM通常表示为

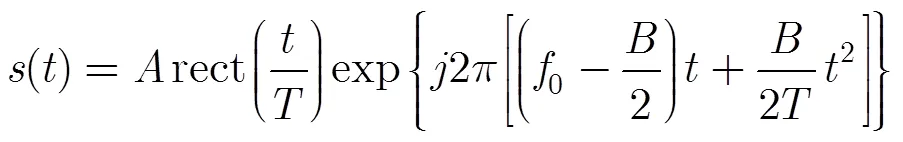
加权方法的传输函数一般表示为[16]：

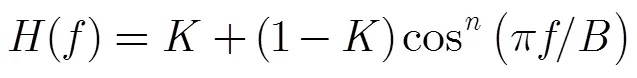
常规加权方法的峰值旁瓣级和主瓣展宽系数如表1所示。

常规加权方法在抑制旁瓣的同时，均会造成不同程度的主瓣展宽。在多亮点探测、分辨和识别应用中，人们不仅希望探测系统具有较低的输出距离旁瓣，还希望系统保持较高的距离分辨力。主瓣展宽造成距离分辨力下降，这在分辨力要求苛刻的场合是难以被接受的。

表1加权函数性能

加权方法汉明3:1锥比余弦平方 峰值旁瓣级(dB)-42.56-25.70-31.70 主瓣展宽系数1.471.211.62

3 主瓣不展宽旁瓣抑制方法

匹配滤波处理具有与发射信号带宽直接相关的距离分辨力，而加权处理具有较好的旁瓣抑制效果。为了兼顾距离分辨力和旁瓣抑制效果，本文提出一种将匹配滤波处理和加权处理相结合的非线性处理方法，该方法的信号处理框图如图1所示。

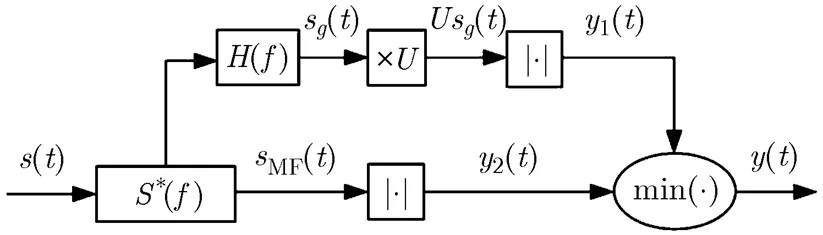
图1 本文方法的处理框图

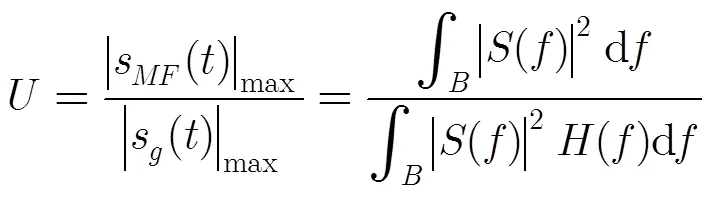
3.1 主瓣宽度分析

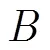
本文方法输出曲线和汉明加权输出曲线的-3 dB主瓣展宽比较如图3所示，参数设置与图2相同。图3表明，本文方法的-3 dB的主瓣展宽明显低于常规加权方法，因此在等强度近邻目标分辨上较常规加权方法有优势。

3.2旁瓣水平分析

由式(7)可知，本文方法的输出旁瓣总是不高于对应加权方法的输出旁瓣，保持了加权方法的旁瓣抑制性能。

本文方法输出曲线和汉明加权输出曲线的旁瓣水平比较如图4所示，参数设置与图2相同。图4表明，本文方法同汉明加权类似，可以较好地抑制主瓣范围外的旁瓣。

3.3检测性能分析

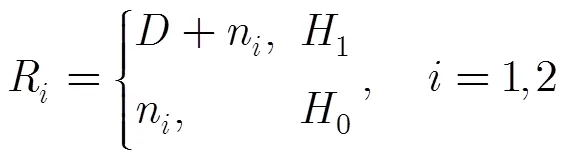
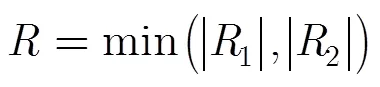
综合主瓣宽度、峰值旁瓣级和检测性能分析结果，文中提出的非线性处理方法与对应的加权处理相比，在保持加权处理旁瓣抑制效果的同时，保持了匹配滤波处理的-3 dB主瓣宽度，而且检测性能得到了小幅度提高。此外，该方法仅对匹配滤波输出数据和加权处理输出数据做了归一化和取小值处理，附加的存储空间代价和计算代价均较小，具有较好的工程适用性。

图2 汉明加权的主瓣展宽

图3 本文方法和汉明加权的主瓣比较

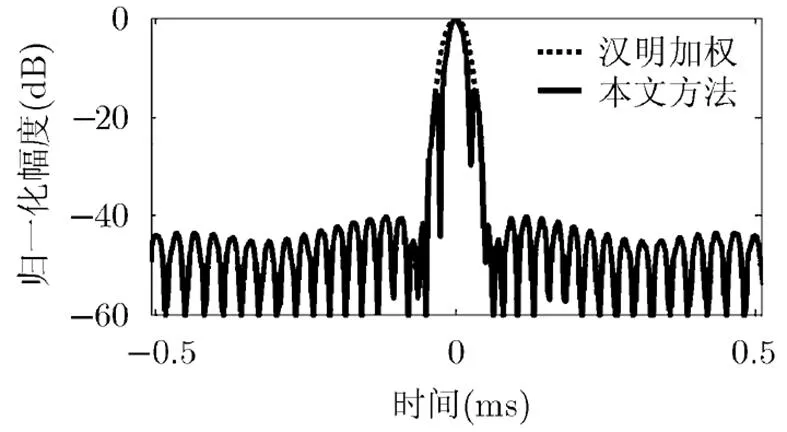
图4 本文方法和汉明加权的输出旁瓣比较

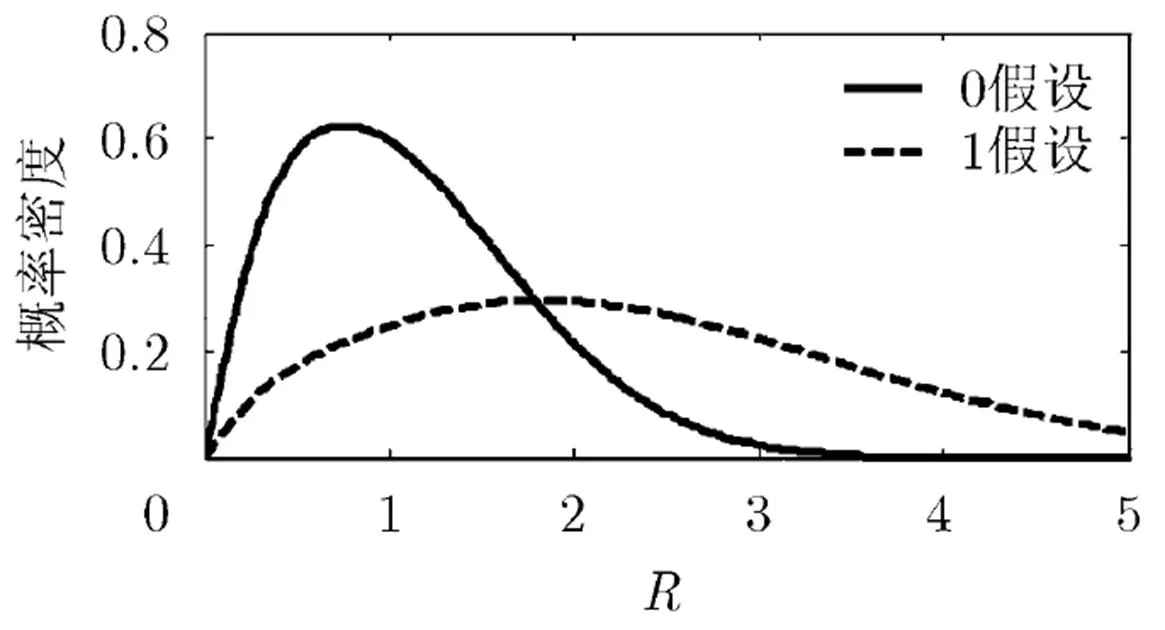
图5 两种假设下R的概率密度函数曲线

图6 检测性能比较

4 仿真分析和试验结果

为评估本文方法性能，以声呐应用为例分别进行了仿真分析和湖上试验。

4.1仿真分析

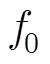
为评估本文方法的旁瓣抑制性能，重新设置目标参数为：在时延41.5 ms处存在强度为0 dB的强目标，在时延41.8 ms处存在强度为-24 dB的弱目标。其它设置不变。仿真得到发射LFM信号时，匹配滤波、汉明加权、3:1锥比加权、余弦平方加权以及以上述3种加权处理为基础的本文方法的弱目标探测结果，如图8所示。图8中的仿真结果验证了本文方法的旁瓣抑制效果和对应的加权方法一致，能够克服匹配滤波输出旁瓣较强从而掩盖弱目标的缺陷。从旁瓣抑制的角度，本文方法保留了加权处理输出旁瓣低的优点，克服了匹配滤波输出旁瓣较高的缺点。

为评估本文方法的检测性能，参数设置为：在时延41.5 ms处存在强度为0 dB的强目标；发射信号、采样率和声速参数不变；输入信噪比-10 dB。仿真得到发射LFM信号时，匹配滤波和以3种典型加权处理为基础的本文方法的弱输入信噪比下的目标探测结果，如图9所示。图9中的仿真结果验证了本文方法的检测性能与匹配滤波处理基本相当。

4.2湖上试验

试验中在距声源31.1 m(对应时延约为41.5 ms)附近放置两个间距0.15 m(对应时延间距0.2 ms)的球目标，目标强度相差1.5 dB。LFM参数与仿真设置相同。试验中的发射LFM波形如图10所示。接收波形受到背景噪声、干扰目标散射和信道传输畸变等多种因素的影响，与发射波形相比产生了明显畸变。接收波形如图11所示，直接由接收波形难以分辨两个目标亮点。由湖上试验数据得到的匹配滤波输出、汉明加权输出和本文方法输出的时间-幅度曲线如图12所示。

图7 等强度邻近目标分辨

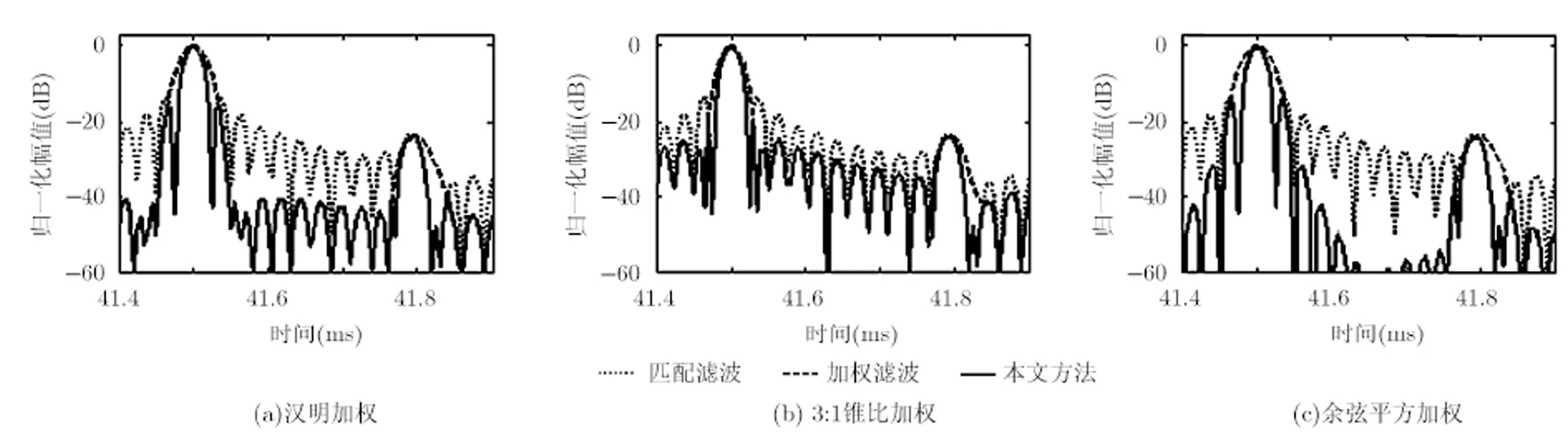
图8 弱目标探测

图9 低输入信噪比下的输出波形

由图12的湖上试验结果可明显看出，本文方法输出曲线的-3 dB主瓣宽度和匹配滤波处理相同，明显窄于相应加权方法的主瓣宽度；而该方法的输出旁瓣水平和相应加权方法相当，可以有效降低匹配滤波的输出旁瓣。试验结果表明本文方法兼顾了主瓣宽度不展宽和旁瓣抑制需求，验证了理论分析结论的正确性。

5 结束语

LFM信号是雷达和声呐系统中常用的脉冲压缩信号，但是经过匹配滤波处理之后的脉冲压缩输出具有较高旁瓣。为了抑制LFM对应的输出旁瓣，人们采用了多种窗函数加权旁瓣抑制方法，但是这些加权方法在抑制旁瓣的同时造成了输出主瓣不同程度的展宽，降低了系统距离分辨力。

为了抑制LFM输出旁瓣的同时，兼顾匹配滤波处理的高分辨力，本文提出了一种主瓣不展宽旁瓣抑制方法。该方法匹配滤波输出和加权输出在幅度归一化之后，进行非线性逐点取小值处理。理论分析和试验结果表明，该方法兼取了匹配滤波处理的高距离分辨力和加权方法的旁瓣抑制性能。此外，该方法附加的存储空间代价和计算代价均较小，便于工程应用。在多亮点目标要害部位定位，目标精确成像，多目标分辨等应用场合中，该方法具有重要价值。

图10 湖试中的发射LFM波形

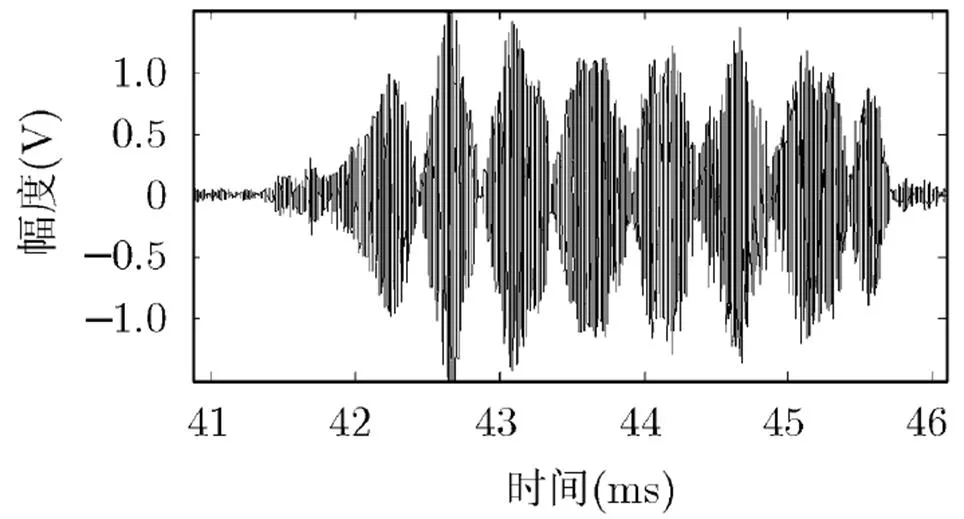
图11 湖试中的接收波形

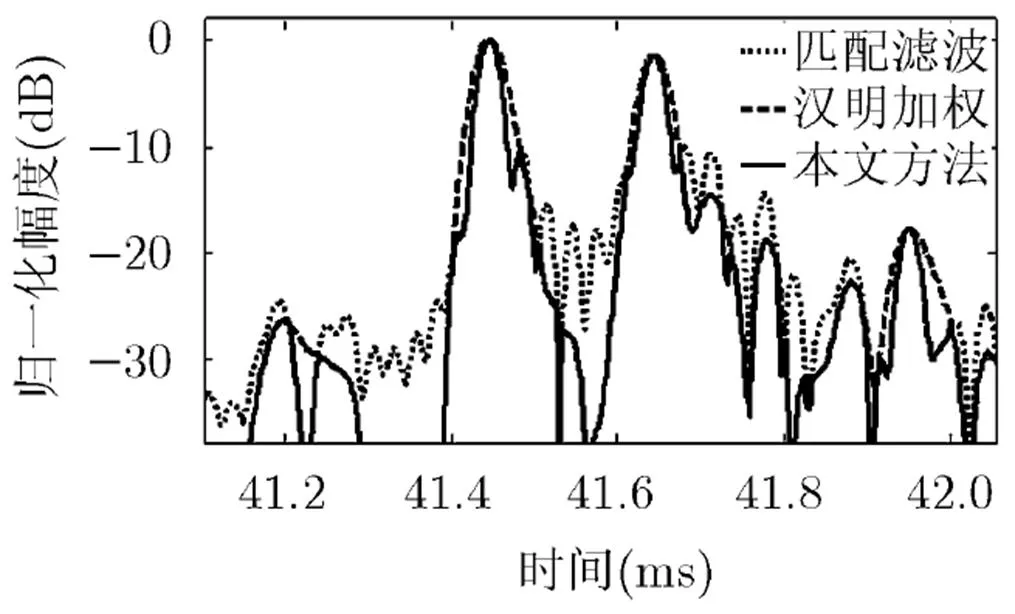
图12 湖试的时间-幅度曲线

[1] Witte E D and Griffiths H D. Improved ultra-low range sidelobe pulse compression waveform design[J]., 2004, 40(22): 1448-1450.

[2] Rao V N and Rajeswari K R. Target detection with cross ambiguity function using Binary Sequences with high discrimination[J]., 2011, 16(4): 8-12.

[3] Govoni M A. Linear frequency modulation of stochastic radar waveform[D]. [Ph.D. dissertation], Hoboken, NJ, USA, Stevens Institute of Technology, 2011: 7-16.

[4] Huo Kai, Deng Bin, Liu Yong-xiang,High resolution range profile analysis based on multicarrier phase-coded waveforms of OFDM radar[J]., 2011, 22(3): 421-427.

[5] 邓云凯, 郑远, 胡英辉. 随机调频信号旁瓣抑制及成像[J]. 电子与信息学报, 2009, 31(8): 1886-1891.

Deng Yun-kai, Zheng Yuan, and Hu Ying-hui. Sidelobe suppression and imaging of the random fm signal[J].&, 2009, 31(8): 1886-1891.

[6] Kim K T. Focusing of high range resolution profiles of moving targets using stepped frequency waveforms[J].,&, 2010, 4(4): 564-575.

[7] Patton L, Frost S, and Rigling B. Efficient design of radar waveforms for optimized detection in colored noise[J].,&, 2012, 6(1): 21-29.

[8] Luszczyk M and Labudzinski A. Sidelobe level reduction for complex radar signals with small base[C]. Proceedings of 19th International Radar Symposium, Warsaw, Poland, 2012: 146-149.

[9] Ai X, Li Y, Wang X,Some results on characteristics of bistatic high-range resolution profiles for target classification [J].,&, 2012, 6(5): 379-388.

[10] White P R and Locke J. Performance of methods based on the fractional Fourier transform for the detection of linear frequency modulated signals[J]., 2012, 6(5): 478-483.

[11] Klinger O, Stern Y, Schneider T,Long microwave- photonic variable delay of linear frequency modulated waveforms[J]., 2012, 24(3): 200-202.

[12] Curlander J C and Mcdonough R N. Synthetic Aperture Radar, Systems and Signal Processing[M]. New York: John Wiley & Sons, 1991: 165-187.

[13] Lewis B L. Range-time-sidelobe reduction technique for FM- derived polyphase PC codes[J]., 1993, 29(3): 834-840.

[14] Boukeffa S, Jiang Y, and Jiang T. Sidelobe reduction with nonlinear frequency modulated waveforms[C]. IEEE 7th International Colloquium on Signal Processing and Its Applications, Penang Island, Malaysia, 2011: 399-403.

[15] 林茂庸, 柯有安. 雷达信号理论[M]. 北京: 国防工业出版社, 1981: 115-199.

Lin Mao-yong and Ke You-an. Theory of Radar Signals[M]. Beijing: Publishing House of Defense Industry Press, 1981: 115-119.

[16] Richards M. Fundamentals of Radar Signal Processing[M]. New York: McGraw-Hill, 2005: 188-198.

[17] 王继胜. 小平台剖面声呐的信号处理技术研究[D]. [博士论文], 哈尔滨: 哈尔滨工程大学, 2007: 121-128.

Wang Ji-sheng. The signal processing techniques study for profiling sonar based on small carrier[D]. [Ph.D. dissertation], Harbin: Harbin Engineering University, 2007: 121-128.

[18] Doisy Y, Deruaz L, Ijsselmuide S P,Reverberation suppression using wideband Doppler-sensitive pulses[J]., 2008, 33(4): 419-433.

[19] Levanon N. New waveform design for magnetron-based marine radar[J].,&, 2009, 3(5): 530-540.

[20] Rasool S B and Bell M R. Biologically inspired processing of radar waveforms for enhanced delay-Doppler resolution[J]., 2011, 59(6): 2698-2709.

[21] Simon M K. Probability Distributions Involving Gaussian Random Variables: A Handbook for Engineers, Scientists and Mathematicians[M]. New York: Springer, 2002: 79-87.

郭 瑞： 男，1980年生，博士生，讲师，研究方向为主动信号设计.

蔡志明： 男，1962年生，博士，教授，博士生导师，研究方向为水声信号处理.

姚直象： 男，1976年生，博士，副教授，硕士生导师，研究方向为水声信号处理.

Sidelobe Suppression Method of Linear Frequency Modulated Signal without Mainlobe Widening

Guo Rui Cai Zhi-ming Yao Zhi-xiang

(,,430033,)

Weighting methods, such as Hamming window, can suppress the peak sidelobe level of matching filter output of Linear Frequency Modulated (LFM) signal, but they also cause obviously mainlobe widening which results in range resolution worsening. Considering requirements of both sidelobe suppression and range resolution, a novel sidelobe suppression method without mainlobe widening is proposed. The amplitude outputs of matching filter and weighting window are firstly normalized, and then compared point by point, finally the minimum value of each point is chosen as the output data. This method fuses both merits of matching filter and weighting processing. The -3 dB mainlobe widening coefficient of the proposed method is only 1 compared with matching filter, and sidelobe suppressing performance is equivalent with the employed weighting window. Simulation results and lake experiment demonstrate the validity of the proposed method.

Signal processing; Linear Frequency Modulated (LFM) signal; Sidelobe suppression; Mainlobe width; Matching filter; Hamming weighting

TN911.7; TB56

A

1009-5896(2014)02-0298-06

10.3724/SP.J.1146.2013.00421

郭瑞 arys66@sina.com

2013-04-01收到，2013-11-07改回

国家自然科学基金(51109218, 60902071)，东南大学水声信号处理教育部重点实验室开放研究基金(UASP1303)和海军工程大学科研基金(HGDQNEQJJ12008, HGDQNJJ11027)资助课题