双星运行轨道的研究
2014-05-25李学生
李学生
(山东大学物理学院 山东济南 250100)
双星运行轨道的研究
李学生
(山东大学物理学院 山东济南 250100)
文章首先把双星运动看做二体问题,研究以一个星体为参照系,另一个星体的轨迹为圆锥曲线,以系统的质心为参照系,每一个星体的轨迹也是圆锥曲线,然后提出了行星与恒星之间也是双星现象,地球与月球之间也是双星现象,解释了困扰物理学与天文学多年的行星运行轨道的共面性、公转的同向性难题,指出了研究行星运行轨道时惯性质量应当用折合质量计算.
双星现象 折合质量 行星运行轨道的共面性 行星公转的同向性 万有引力定律的平权性
1 问题的提出
物理双星运动属于二体问题,早在1687年,牛顿发现万有引力定律后不久,似乎已经彻底解决,但是现代物理学教材中一般只是指明双星围绕系统的质心旋转,没有说明如果以一个星体为参照系,另一个星体运动轨迹的形状.现代天文学中双星轨道拟合业已成为天体测量和天体力学的一个共同的热点课题,有关研究有了长足的进展,同时也促进了天体物理相应领域的发展.
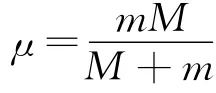
在二体问题中,由于两个物体都不是惯性系,如果以一个物体为参照系,另一个物体的惯性质量必须用它们的折合质量(约化质量)μ代替,即其中m和M分别为两个物体的质量,这样在非惯性系中就可以利用牛顿第二定律了.但是万有引力的计算中只能利用物体的实际质量,此时引力质量不等于惯性质量,因此在双星现象中,如果以其中一个星体为参照系,可利用折合质量代替另一个星体的惯性质量进行计算.
2 运行轨道的计算
我们设星体A和星体B两个星体的质量分别为M和m,星体A中心所在位置为复平面之原点O,在时刻t,星体B位于点P.即

这里r=r(t),θ=θ(t)均是t的函数,分别表示Z(t)的模和辐角.于是星体B的速度为

这是两个未知函数的二阶微分方程组.在确定某一星体B的轨道时,需要加上定解条件.我们设当t=0时,星体B正处于与星体A距离最远的位置,而此时位于正实轴上,距原点O为r0,星体B的线速度为v0,那么就有初始条件
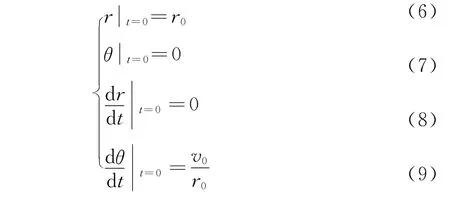
式(4)~(9)就是星体B绕星体A运行的轨迹的数学模型.将式(4)乘以r,即得
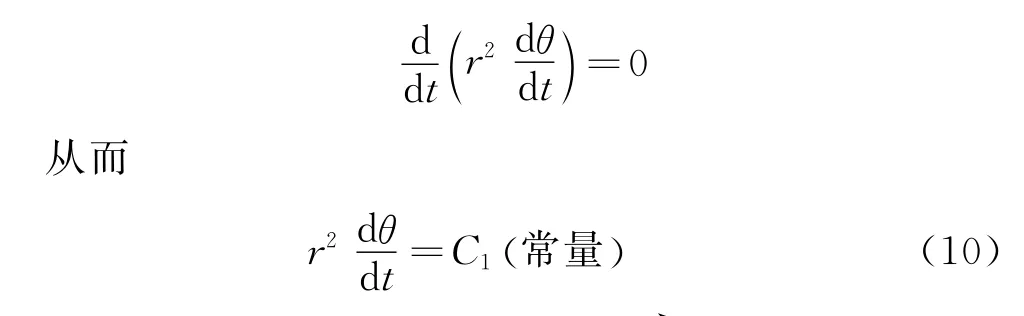
100的面积等于
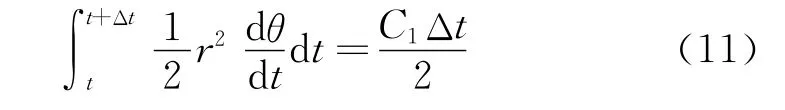
显然,这正是开普勒第二定律:从星体A指向星体B的线段在单位时间内扫过的面积相等.将式(10)改写后代入式(5)得

于是我们得到了星体B运动形式的较为简单的数学模型
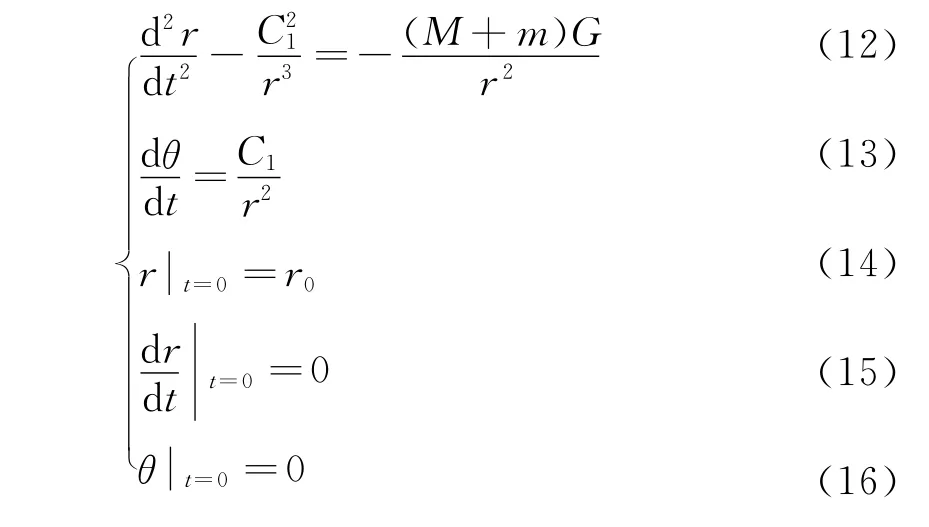
为求得星体B的轨迹方程,要消去变量t,令
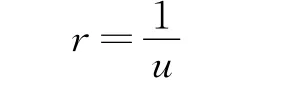

那么式(13)可以写为这就是星体B的轨迹方程,是一条平面二次曲线.由于星体B绕星体A运行,故必有0<e<1,这样我们得到了开普勒第一定律:星体B的轨道是以星体A为一个焦点的椭圆.
由于r在t=0时取到最大值r0(星体B与星体A距离最远的点),而θ=0,这意味着此时函数cos(-θ0)取到最小值-1,于是就有
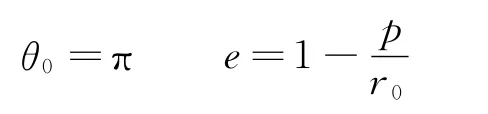
从而星体B轨迹的方程为
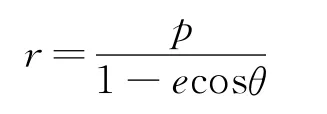
从上面的推导可以看出在双星现象中由于以其中一个星体为参照系另一个星体的轨迹都是圆锥曲线,所以两个星体的轨道共面.
3 星体运行速度的计算
设星体B的运行周期为T,那么利用开普勒第二定律即式(11),有
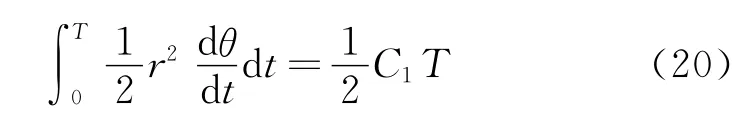
式(20)左端为星体B轨迹椭圆所围的面积,记为S,由于椭圆的半长轴

半短轴

从而有
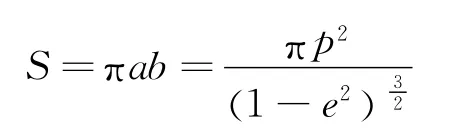
将上式代入式(20),解得
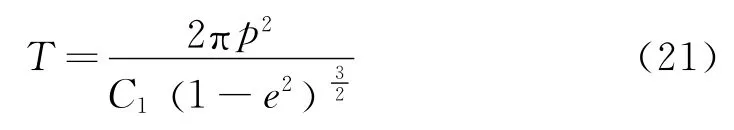
由于星体B的运行满足开普勒第二定律即式(11),而该式可改写为
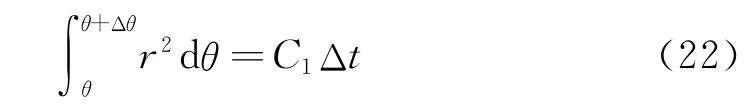
从而可得
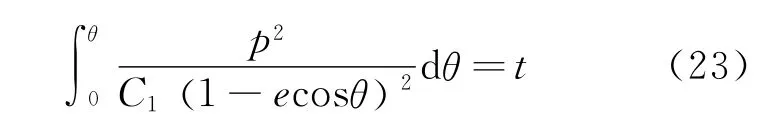
如果我们要求t=T1时相应的θ和r,则意味着首先要解方程
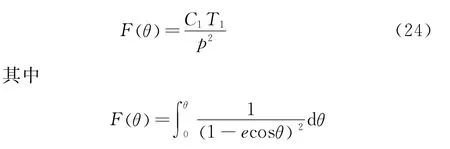
在求出了t=T1时的θ=后,立即可以由式(19)得到相应的r,再用式(13)求出此时星体B的角速度继而得到线速度.
4 以双星系统的质心为参照系
在忽略了其他对于双星的作用时,只考虑双星构成的孤立系统,则质心将做匀速直线运动或静止.星体B位于P点,星体A位于S点,质量分别是m 和M,质心在C点,星体B距质心为r1,星体A距质心为r2,相距为r,如图1所示.

图1
可将质心看作惯性系.在惯性系中,对于行星B应用牛顿第二定律有
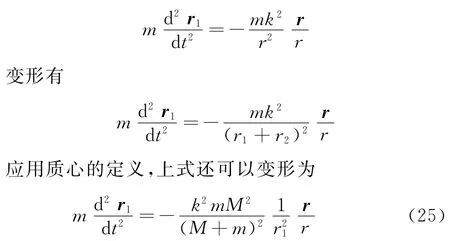
所以星体B绕质心做圆锥曲线运动.同理,可以推导出星体A也绕质心做圆锥曲线运动.
5 天文学中的应用
宇宙中的二体问题,如果只考虑万有引力,同时忽略其他星体的影响,以质心为参照系都是双星现象,以一个星体为参照系另一个星体的运动轨迹都是圆锥曲线轨道,只有这样才满足万有引力定律的平权性,符合科学的简单性原则.在研究行星运行轨道时,恒星和行星都不是严格的惯性系,以质心为参照系,才可以按照惯性系处理.现代物理学研究太阳系运行时把太阳当做惯性系只是近似成立,其实不完全满足万有引力定律的平权性原则,地太系统也应当看做是双星现象.在经典力学中日心说与地心说都是正确的,与广义相对论的观点一致,只不过由于太阳的质量远大于行星的质量,其他行星的扰动较小,把太阳按照惯性系计算误差较小,研究行星的运行轨道比较简单,这也是哥白尼的日心说优于地心说的原因.
在太阳系中由于太阳的质量远大于所有行星以及其卫星的质量之和,因此每个行星与太阳组成系统的质心与太阳系的质心相距很近,可以近似认为是太阳的质心以太阳系的质心为一个焦点做椭圆运动.由于太阳系中太阳和行星是双星现象,根据前面的计算可以得出双星运行的轨道始终共面,因此行星始终也和太阳共面——始终在太阳运行的轨道所在的平面上,这样就可以解释为何太阳系中所有行星的运行轨道基本共面这个困扰天文学多年的难题,当然由于每个行星与太阳组成系统的质心不完全重合以及其他行星的扰动等因素,因此行星的运行轨道有一定倾角.从双星运动的轨迹可以得知,行星的公转方向与太阳的公转方向相同,这样就可以解释为何行星的公转方向相同以及大部分行星的公转方向相同(公转方向不相同的金星可能时受到太阳系外其他星体碰撞的影响)这个疑难问题,类似地可以理解卫星运动同向性、轨道共面性等问题,有些学者从太阳系的形成过程解释轨道的共面性,但是无法理解几乎每一个行星的卫星都具有共面性、同向性的问题,不可能都是巧合.也就是说,行星与它的卫星之间也应当认为是双星现象,例如尽管地月系统的质心在地球上,但是与地球的质心并不重合,应该是地球的质心绕着地月系统的质心运动,选择地月系统的质心为参照系才能直接利用经典力学处理,如果以地球为参照系,月球的惯性质量也应当用地球、月球的折合质量计算.类似地以太阳为参照系,地球的惯性质量应当用太阳与地球的折合质量代替,以恒星为参照系,行星的惯性质量与引力质量相等只是近似成立.
1 Einstein A.相对论的意义.北京:科学出版社,1961.16
2 福克B A.空间、时间和引力理论.北京:科学出版社,1965.19
3 Einstein.相对论:相对论的本质.Einstein文集.北京:商务印馆,1976.455
Studyon the Orbit of Double- star
Li Xuesheng
(School of Physics,Shandong University,Jinan,Shandong 250100)
the thesis firstlytreats the relative motion of double- star as motion issue of two separate objects.Once taking one star of the double- star as frame of reference,we result in the orbit of the other star is taper curve.If we just take mass center of system as frame of reference,we consequentlyresult in both orbits of the double- star are taper curves.And finally,we arrive at our conclusion that relative motion situation between related planets and star are too in double-star model,even the earth and the moon are double- star too.This of course gives demonstrative answers to issues of coplanarity and uniform orientation of planet revolution orbits around star,which virtually puzzled modern physics and astronomy many years.And of course,it is still necessary to point out herein,when we come to study planet obit,the planet mass in calculation should be the conduplicate mass.
double- star phenomena;equivalent quality;orbit coplanarity of planet;uniform orientation of planet revolution orbit;affirmative law of universal gravitation
2014- 03- 04)
