平抛运动试题的灵活运用与一题多解

马光明

（甘肃省临夏回民中学 甘肃临夏 731100）

平抛运动试题的灵活运用与一题多解

马光明

（甘肃省临夏回民中学 甘肃临夏 731100）

笔者在讲解高一平抛运动练习时遇到这样一道题：

【题目】如图1所示，斜面AB的倾角为30°，小球从A点以初速度v0水平抛出，恰好落在B点．求从抛出开始经多长时间与斜面间的距离最大？且最大距离为多少？

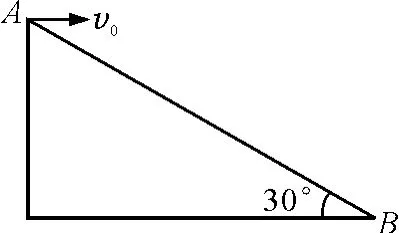
图1

思路1：这道题考查平抛运动的规律，关键是明确小球在什么条件下与斜面间的距离最大．有些学生根据在地面上物体的斜抛运动，最高点速度方向与地面平行，推出当小球的速度方向与斜面平行时，小球离斜面最远．

解法1：当小球运动方向与斜面平行时，小球与斜面的距离最大，如图2所示，有

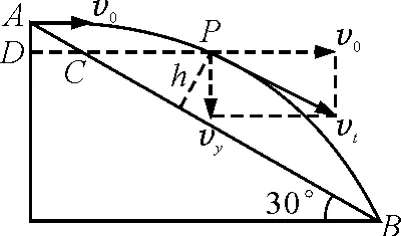
图2

水平位移

最大距离为

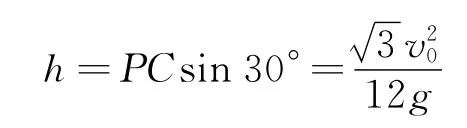
思路2：我们可以将小球的平抛运动沿着斜面方向和垂直于斜面方向分解，当垂直于斜面方向的速度为零时，小球与斜面间的距离最大．

解法2：如图3建立直角坐标系，以沿斜面方向为x轴，垂直于斜面方向为y轴．

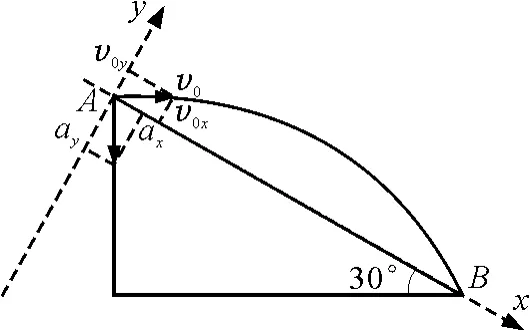
图3

因为小球沿y轴方向做匀减速直线运动，所以当vy＝0时，小球离斜面最远，经历的时间为t

思路3：运用数学知识，求极值．建立小球离斜面的高度h与时间t的函数关系式，讨论当t为何值时，h有最大值的问题．

解法3：在轨迹上任找一点P，小球运动至P点所经历的时间为t，离斜面高度为h，则由平抛运动的规律知，水平位移和竖直位移分别为

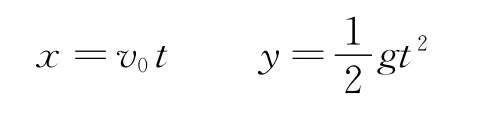
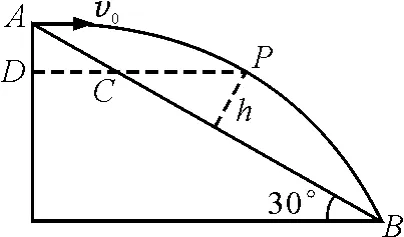
图4

如图4由几何知识得

点评：平抛运动一般可分解为水平方向的匀速直线运动和竖直方向上的自由落体运动．运动的分解一般按运动的实际效果分解，看物体参与了哪几个分运动，但不应拘泥于按效果分解，关键要视问题处理的方便，怎样方便就怎样分解．方法1采用了对临界状态的分析，小球速度方向与斜面平行时，离斜面的距离最大，实际上此时垂直于斜面方向上的速度为零，与方法2有异曲同工之妙．方法2灵活运用了运动的分解，思维及过程简洁明了．方法3注重对数学知识的应用，过程繁琐，但对能力的要求较高，有利于培养学生应用数学知识处理物理问题的能力．

总之，对于物理问题我们应采用不同的角度去分析，尝试多种方法去解，灵活运用所学知识，才能提高我们的解题能力．

2014- 06- 23）