弹性球壳声散射对矢量传感器测向精度的影响

梁国龙，庞福滨，张光普

（哈尔滨工程大学水声技术重点实验室，哈尔滨 150001）

式中：θ′是球坐标系中的观察点位置和直角坐标系中观察点位置的夹角，显然θ′＝0。因此：

弹性球壳声散射对矢量传感器测向精度的影响

梁国龙，庞福滨，张光普

（哈尔滨工程大学水声技术重点实验室，哈尔滨 150001）

由无指向性的声压传感器和具有偶极子指向性的振速传感器组成的矢量传感器，被应用于水声技术的各个领域；在实际应用过程中，常常把矢量传感器固定在某个水下平台上，而平台产生的散射场会使矢量传感器的接收声场发生畸变，进而影响其测量结果。本文以实际应用为背景，建立了弹性球壳障板的声散射场对矢量传感器测向性能影响的模型，并通过仿真分析了不同入射频率、不同观察距离、不同球壳厚度和半径条件下障板对矢量传感器测向精度的影响，研究结果为矢量传感器在水声测量中的应用提供理论支撑。

弹性球壳；散射场；矢量传感器；测向精度

声矢量传感器由声压传感器和质点振速传感器组成，可以共点、同步地测量声场中的声压和质点振速。随着声矢量传感器技术和信号处理技术的发展，它被日益广泛地应用于水声技术各个领域。矢量传感器种类繁多，其中同振式矢量传感器以本身不产生明显的声场畸变、指向性好、性能更稳定，而在水声工程领域中适用较多。当声矢量传感器被应用于水下小平台探测时，会不可避免地受到这些水下载体的声散射影响，进而影响其测向精度。近年来，很多学者研究了障板对矢量传感器测量的影响，生雪莉等［1］将鱼雷壳体近似为球对称的封闭空气腔，分析了球形软障板对矢量传感器指向性的影响；时胜国等［2－3］分析了弹性球壳声衍射对矢量传感器测量的影响，并且考虑了弹性球壳的共振情况，得出了弹性球壳障板对矢量传感器测量影响的规律；嵇建飞等［4－5］推导了软球、软椭球障板条件下矢量传感器接收声压和质点振速表达式，并进行了实验验证，实验结果与理论分析相符合；Kosobrodov等［6］从理论上分析了钛合金薄壳近场散射对矢量传感器的影响，并进行了实验分析；陈亚林等利用ANSYS和SYSNOISE软件分析了刚性圆柱组合体声散射对矢量传感器指向性的影响，并进行了实验验证。杨德森等［7］极速散了球壳障板的近场矢量特性，结果表明质点振速方向和声源方位不一致，声压与质点振速不再同相。上述文献多偏重于不同障板条件下声散射对声场中声压和质点振速指向性的影响，未分析障板散射对矢量传感器测向的影响。本文以弹性球壳为研究对象，建立了障板散射对矢量传感器测向影响的模型，分析了不同入射频率和观察角度、不同观察点位置、球壳厚度条件下障板对矢量传感器测向精度的变化规律。分析结果为矢量传感器在障板平台的测向应用提供了理论参考。

1 弹性球壳在平面波下的测向影响计算模型

令坐标系原点和弹性球壳中心重合，取球壳内径为a1，外径为a2，球壳厚度为h，球壳内外区域介质密度分别为p1和p2，声传播速度分别为c1和c2，球壳密度为ρM。矢量传感器位于M点，oM与x轴正向夹角为θ，矢量传感器距球心距离为r，见图1所示。

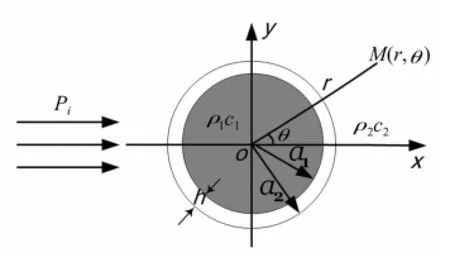
图1 弹性球壳与入射平面波坐标关系示意图Fig.1 Diagram of coordinate relation between elastic spherical shell and incident plane wave

取入射平面波为［9］：

式中：p0为单频入射平面波的声压幅值，ω＝2πf，f为单频入射平面波频率，k2为波数，k2＝ω／c2，上式在球坐标系中可以展开为：

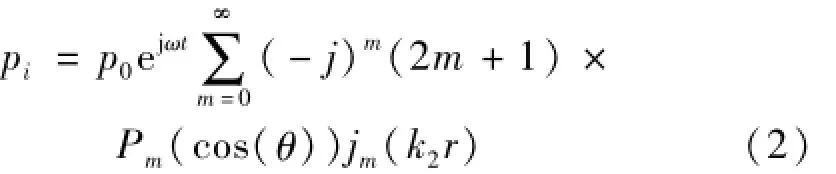
声波透过弹性球壳的透射声压p1和在弹性球壳上的散射声压ps可以写成［10］：

式中：Am，Bm是常数，k1，k2是波数。Pm（cos（θ））为勒让德函数，jm（k1r）为球贝塞尔函数，h（2）m为第二类球汉克尔函数。

如果忽略薄壁球壳体的对称振动，则球壳内外两面速度相等。设球壳外声压为p2＝pi＋ps，利用壳体的两面声压差与它们的机械阻抗关系式：

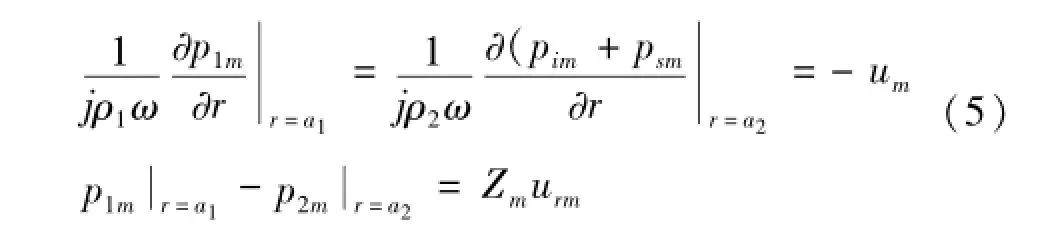
式中：下标m表示所有量取对于m号振型情况的值，Zm是壳体的机械阻抗。根据上述边界条件，将式（2）、（3）、（4）表示的球壳内外声波的形式代入式（5）中，可得：

式中：a为球壳半径，σ为泊松比，E为材料的杨氏模量。

由式（6）和尤拉方程u＝－（∫▽p d t）／ρ可以求得球壳外质点的径向振速ur和垂直半径方向的振速分量uθ：

式中：θ′是球坐标系中的观察点位置和直角坐标系中观察点位置的夹角，显然θ′＝0。因此：

2 数值计算和分析

假设弹性球壳放在无限的、均匀的水流体介质中，球壳内部充满空气；矢量传感器柔性地安装在弹性球壳外，忽略矢量传感器的声散射及其对弹性球壳的影响。取弹性球壳的几何参数为：外半径a2为0.533／2 m，球壳厚度h为0.005 m，弹性球壳密度ρM＝7 850 kg／m3，泊松比σ＝0.28，杨氏模量E＝2.1×1011N／m2。弹性球壳内部介质为空气，密度ρ1＝1.29 kg／m3，声速c1＝346 m／s，球壳外部介质为水，密度ρ2＝1 000 kg／m3，声速c1＝1 500 m／s。设入射波幅值为1 Pa，矢量传感器和球心距离为r，下面分四种情况讨论。

2.1 不同入射频率和观察角度情况

由式（12）计算弹性球壳散射对矢量传感器测向的影响。图2为不同入射频率条件下，r＝0.5 m处观察角度分别为120°和150°时球壳散射对矢量传感器测向的影响。从中可以看出，在频率f＜1 kHz的低频段，散射波的幅值很小，虽然散射波与入射波的相位差较大，但入射波起主要作用，矢量传感器的测向精度较高；在1 kHz＜f＜2.5 kHz的中频段，由于入射波频率与球壳共振频率接近，弹性球壳发生共振。从图2（a）中可以看出散射波幅值曲线在1 300 Hz，1 650 Hz，1 980 Hz，2 480 Hz等处出现明显的谐振峰，此时散射波与入射波的相位差变化也较为剧烈，因此矢量传感器的测向精度较低；在2.5 kHz＜f＜4 kHz的高频段，虽然散射波与入射波的相位差起伏变化，但散射波幅值整体较为稳定，因此矢量传感器的测向精度较高，但在球壳共振频率的倍频点处散射波的幅值较大，散射波与入射波的相位差起伏也较大，使得球壳共振频率的倍频点处矢量传感器测向误差较大。

图2 不同入射频率时球壳散射对矢量传感器测向影响Fig.2 Influences of scattering wave on DOA estimating of vector sensorwith different incident frequencies

图3 不同观察角度时球壳散射对矢量传感器测向影响Fig.3 Influences of scattering wave on DOA estimating of vector sensor with different observing angles

从图2中可以发现，不同观察角度条件下矢量传感器的测向精度差别较大。图3给出了r＝0.5 m处观察角度从0°～180°变化时球壳散射对矢量传感器测向的影响。从图3（a）可知，不论观察角度如何变化，当入射频率在1 kHz以下时，散射波的幅值很小，表现为声波的绕射作用。1 kHz以上时，球背部（观察点位于x正轴区域）散射波的幅值较球前方（观察点位于x负轴区域）整体偏大，在球壳的共振频率及共振频率的倍频点处散射波幅值较为突出。即随着入射频率的增高，球背部的散射波逐渐增强，与入射波产生干涉，在球的背面出现声影区，故观察点位于球背部时矢量传感器的测向精度低。在球前方，散射波幅值较大的点分布在弹性球壳的共振频率及共振频率的倍频点处，在其它频率处散射波幅值较低；但观察角度从100°起，散射波和入射波有两条双曲线状的干涉带，在此区域内矢量传感器测向精度较低。而在90°±10°的扇形区域内，由于入射波y方向质点振速远大于x方向质点振速，故此区域内除球壳的共振频率及其倍频点以外，其它频率处矢量传感器的测向精度较高。

2.2 不同观察距离情况

图4给出了观察角度为150°时，矢量水听器距球心位置在0.5 m～6 m之间时球壳散射对矢量传感器测向的影响。从图中可以发现，近距离时，由于声波的绕射作用，在f＜1 kHz的低频段散射波的幅值较小；在1 kHz＜f＜2.5 kHz的频段，即球壳共振频率区域，散射波的幅值较大，这时球壳的共振在声场中起主要作用；在2.5 kHz＜f＜4 kHz的高频段，除了球壳共振频率的倍频点处散射波幅值较大外，其余频点散射波幅值较小。随着观察距离的增加，散射波的幅值整体减小，除弹性球壳的共振频率及其倍频点处散射波幅值较大以外，入射波起主要作用。随着观察距离的改变，散射波与入射波之间的相位差起伏变化，如图4（b）所示。因此，在近距离处低频时矢量传感器的测向精度较高，在球壳的共振频率及其倍频点处矢量传感器的测向精度较低；随着观察距离的增加，散射波幅值变弱，在声场中的贡献变小，矢量传感器的测向精度得到提高，但在球壳的共振频率及共振频率的倍频点处误差相对较大。

2.3 不同球壳厚度情况

图5给出了球壳厚度为0.002 5 m，r＝0.5 m，观察角度为120°和150°时球壳散射对矢量传感器测向的影响。从中可以发现，1 kHz以下散射波的幅值较小，入射波起主要作用，故矢量传感器的测向精度较高；在1 kHz～1.8 kHz区域入射波频率与球壳共振频率接近，弹性球壳发生共振，这时矢量传感器测向精度较低；在1.8 kHz～4 kHz区域散射波幅值较为平稳，这时矢量传感器的测向精度较为稳定，但在球壳共振频率的倍频点处幅值较大，矢量传感器的测向精度相对较低。对比图2可以发现，矢量传感器在低频段和高频段测向精度变化不大；在中频段由于球壳的共振频率分布更为集中，且整体往低频偏移，故部分中频区域测向精度得到改善。

2.4 不同球壳半径情况

图6给出了球壳半径为0.533／4 m，r＝0.5 m，观察角度为120°和150°时球壳散射对矢量传感器测向的影响。从图6（a）可以看出，2.5 kHz以下散射波的幅值很小，入射波起主要作用，故矢量传感器的测向精度较高；在2.5 kHz以上散射波幅值开始剧烈变化，在3 220 Hz处由于球壳产生了共振，导致矢量传感器的测向精度较低。相比图2可以发现，减小球壳半径后，球壳的共振频率往高频方向移动，且在观察距离不变的情况下，中、低频处散射波幅值变弱，使得矢量传感器在中、低频段的测向精度得到提高。

图4 不同观察距离时球壳散射对矢量传感器测向影响Fig.4 Influences of scattering wave on DOA estimating of vector sensorwith different observing distances

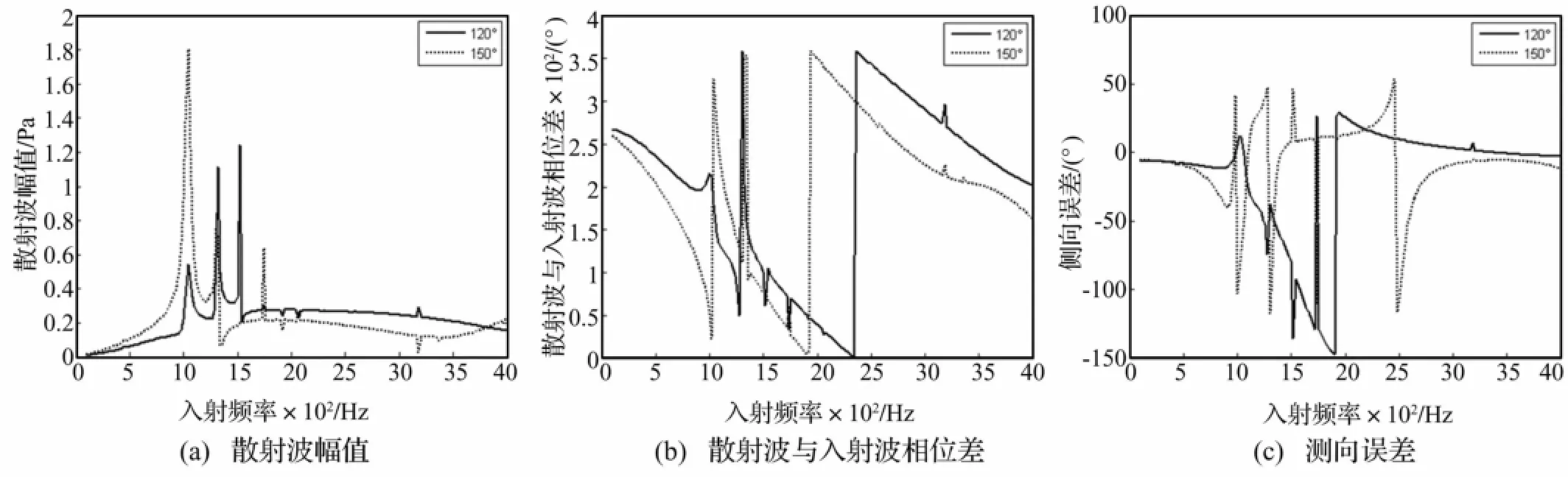
图5 不同球壳厚度时球壳散射对矢量传感器测向影响Fig.5 Influences of scattering wave on DOA estimating of vector sensorwith different shell thicknesses

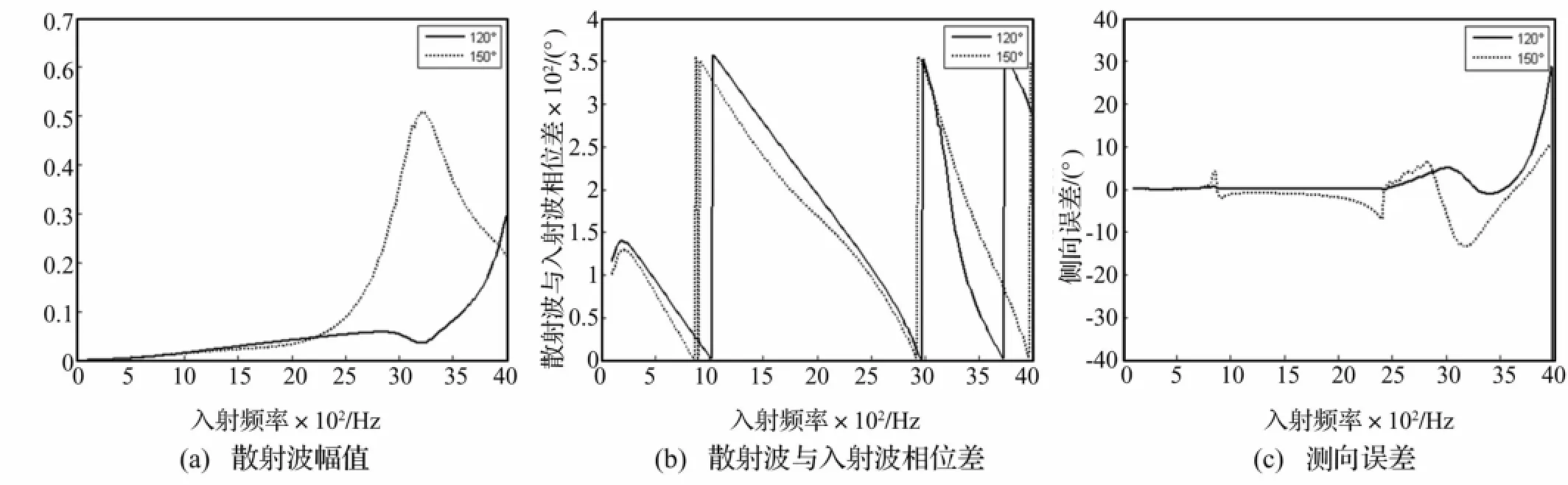
图6 不同球壳半径时球壳散射对矢量传感器测向影响Fig.6 Influences of scattering wave on DOA estimating of vector sensor with different shell radiuses

3 结 论

本文建立了弹性球壳声散射对矢量传感器测向影响的模型，推导了弹性球壳障板条件下球壳外声压和质点振速的数学表达式，计算了内充空气的弹性球壳体和矢量传感器组成的测量系统在不同入射频率和观察角度、不同观察点位置、球壳厚度条件下的测向精度，得出了以下结果：

（1）入射频率小于1 kHz时，由于声波的绕射作用，弹性球壳的散射波幅值较小，矢量传感器的测向精度较高。当入射频率接近弹性球壳的共振频率时，弹性球壳发生共振，此时矢量传感器测向精度较低。

（2）观察点位于球背部时矢量传感器的测向精度劣于观察点位于球前方时的测向精度；当观察点位于90°±10°的扇形区域内时，除球壳的共振频率及共振频率的倍频点以外，矢量传感器的测向精度较高。

（3）近距离处，低频时矢量传感器的测向精度较高，在球壳的共振频率及其倍频点处矢量传感器的测向误差较大；随着观察距离的增大，散射波强度变弱，矢量传感器的测向精度得到提高。

（4）降低弹性球壳的厚度时，球壳的共振频率分布较原来更为集中，且整体往低频偏移，故部分中频区域其测向精度得到改善。

（5）减小球壳半径后，球壳的共振频率往高频方向移动，中、低频处散射波幅值变弱，因此在中、低频段处矢量传感器的测向精度得到提高。

［1］生雪莉，郭龙祥，梁国龙.球形软障板矢量传感器指向性研究［J］.声学技术，2002，9（增刊）：59－60.

SHENG Xue-li，GUO Long-xiang，LIANG Guo-long.Study on the directivity of the vector sensorwith spherical soft baffle plate［J］.Technical Acoustics，2002，9：56－60.

［2］时胜国，杨德森.弹性球壳声衍射声场对矢量传感器指向性影响实验研究［C］.第十届船舶水下噪声学术讨论会论文集，2005：299－303.

［3］时胜国，杨德森，王三德.弹性球壳声衍射对矢量传感器测量影响［J］.哈尔滨工程大学学报，2006，27（1）：84－89.

SHI Sheng-guo，YANG De-sen，WANG San-de.Influences of sound diffraction by elastic spherical shell on acoustic vector sensor measuremen［J］.Journal of Harbin Engineering University，2006，27（1）：84－89.

［4］Ji JF，Liang G L，Huang Y L，et al.Influence on spatial directivity of acoustic vector sensor by soft spherical boundary［C］.International Conference on Computational and Information Sciences，2010.

［5］Ji J F，Liang G L，Wang Y，et al.Influence of prolate spheroidal baffle of sound diffraction on spatial directivity of acoustic vector sensor［J］.Science China Technological Scinences，2010，53（10）：2846－2852.

［6］Kosobrodov R A，Nekrasov V N.Effect of the diffraction of sound by the carrier of hydroacoustic equipmenton the results ofmeasurements［J］.Acoust Phys，2001，47（3）：382－388.

［7］陈亚林，杨 博，马远良.复杂边界条件下矢量传感器的指向性分析及实验研究［J］，声学技术，2006，25（4）：381－386.

CHEN Ya-lin，YANG Bo，MA Yuan-liang.Analysis and experiment study on directivity of vector sensors located on complicated boundaries［J］，Technical Acoustics，2006，25（4）：381－386.

［8］杨德森，朱中锐，时胜国.球形壳体障板声散射近场矢量特性［J］.振动与冲击，2013，32（2）：135－139.

YANG De-sen，ZHU Zhong-rui，SHI Sheng-guo.Acoustic vector characteristics of near fields scattered by a spherical shell baffle［J］.Journal of Vibration and Shock，2013，32（2）：135－139.

［9］何祚镛，赵玉芳.声学理论基础［M］.北京：国防工业出版社，1992.

［10］沈杰罗夫著，何祚镛，赵晋英译.水声学波动问题［M］.北京：国防工业出版社，1983.

［11］时胜国，杨德森.矢量水听器的源定向理论及其定向误差分析［J］.哈尔滨工程大学学报，2003，24（2）：132－135.

SHISheng-guo，YANG De-sen.Acoustic source location by acoustic vector-sensor and its bearing error［J］.Journal of Harbin Engineering University，2003，24（2）：132－135.

In fluences of sound scattering of an elastic spherical shell on DOA estimating accuracy of a vector sensor

LIANGGuo-long，PANG Fu-bin，ZHANGGuang-pu
（Key Lab of Underwater Acoustic Technology，Harbin Engineering University，Harbin 150001，China）

A vector sensor is composed of omni directional sound pressure sensors and a dipole directional particle velocity sensor，and it iswidely used in underwater acoustic fields.But，in actual applications，a vector sensor is usually fixed at an installation platform whose scattering field inevitably distorts the vector sensor's receiving field，thus its measuring results are affected.Here，taking practical applications as a background，a model for influence of sound scattering of an elastic spherical shell on the vector sensor's direction measuring was theoretically built.The influences with different incident frequencies，different observing locations，different shell thickness and radius on the accuracy of direction measuring were analyzed with simulation.The results provided a theoretical support for application of a vector sensor in underwater acoustic measuring.

elastic spherical shell；scattering field；vector sensor；DOA estimating accuracy

TB566

A

国家自然科学基金（51009042，61201411）；中央高校基本科研业务费专项基金资助（HEUCF12502）；水声技术重点实验室基金资助（9140C200802110C2001）

2012－11－19 修改稿收到日期：2013－04－16

梁国龙男，教授，博士生导师，1964年生

庞福滨男，博士生，1987年生