基于延拓与可变余弦窗的经验模态分解改进算法研究

丁雪娟，时培明

（燕山大学电气工程学院，秦皇岛 066004）

基于延拓与可变余弦窗的经验模态分解改进算法研究

丁雪娟，时培明

（燕山大学电气工程学院，秦皇岛 066004）

针对经验模态分解（Empirical Mode Decomposition，EMD）中存在的边界效应及边界发散现象随着筛选层次的增加而增加的问题，提出一种利用延拓与可变余弦窗相结合的改进新方法。首先对信号进行延拓处理，增加一定长度的数据，实现延拓数据与原始信号交界处的光滑过度。其次，根据信号边界的发散程度，在逐层提取各阶本征模函数（Intrinsic Model Function，IMF）之前，在信号两端加上宽度可变的余弦窗函数，使得每一个IMF分量边界发散问题最小化，保证信号有效数据的正确分解，实现EMD边界处理算法的改进。仿真和实例信号分析表明，该方法能较好地抑制EMD边界效应，有效地提取故障信号中的特征信息。

信号处理；经验模态分解；边界效应；可变余弦窗

经验模态分解是Huang首先提出的一种新的自适应的时频分析方法［1］。它根据信号的局部时变特征进行自适应的分解，避免了人为因素，克服了传统方法中的非局域化及非自适应性，具有良好的时频聚集性，适合处理瞬变、调幅或调频等非线性、非平稳信号。自EMD方法问世以来，它就引起了众多学者的广泛关注，已被应用于设备诊断、医学信号分析、语音信号的检测、图像信息分离等领域［2－4］。

边界效应一直是制约EMD发展的一个关键问题，针对这一问题，研究人员已经提出了一些改进方法，如镜像延拓［5］、神经网络延拓［6］、相似极值延拓［7］、波形特征匹配延拓［8］、支持矢量回归机［9］等。但是，这些延拓方法仍然存在一定的误差，导致其边界发散问题依然存在。窗函数可以将延拓误差控制在信号的两端，使其无法（或以较慢速度）向数据内部发展。任达千等［10］提出了窗函数法对抑制边界效应有明显的效果，但指出加窗会改变原始信号，影响分解精度。Qi等［11］提出了在原始信号上加余弦窗函数，虽然对提取低频微弱信号具有一定作用，但是固定窗函数只能抑制特定信号的边界效应，对最后的分解结果有一定的影响。Parey等［12］提出了在IMF分量上加可变余弦窗函数，该方法必须保证每个IMF分量具有明确的物理意义，才能使得方法有效，但是在EMD分解过程中有些微弱低频分量难以筛选出来，无法反映真实的物理过程，使得该方法具有局限性。

本文提出了一种基于延拓与可变余弦窗相结合的改进方法。该方法首先将信号延拓处理，增加一定长度的数据，避免在加窗函数时造成数据的改变。其次，每次提取IMF前，在信号两端加上宽度可调的余弦窗函数，使得包络线变得比较平滑，沿着正确的方向延展。为了降低窗函数带来的误差，该方法设计窗函数的宽度可调，提高了IMF的分解精度。最后对EMD分解得到的IMF进行Hilbert变换，按原始信号长度及位置提取分析结果，得到有效数据的分析结果。仿真和应用实例分析验证了该方法的有效性。

1 EMD边界效应及改进算法

1.1 边界效应

EMD时频分析方法处在发展阶段，其理论还需要不断完善。边界效应是其应用过程中的一个重要问题。EMD分解中由于无法保证数据端点处的极值点，导致求包络平均过程中，会在样条插值时产生数据的拟合误差。并且随着分解的进行，误差不停积累，由端点处向内逐渐传播，严重时会使分解的数据失去意义。同时，用数字方法实现的Hilbert变换是基于Fourier变换的，在对本征模分量进行Hilbert变换时，由于首尾两点的数值不同，导致频谱的泄漏，表现在时频谱图上便是边界效应，影响了时频分析的精度。

1.2 基于延拓和可变余弦窗的边界效应改进算法

在EMD分解过程中，边界效应是在样条差值时产生的拟合误差，从端点附近开始出现，并且逐渐向内“污染”。随着分解的进行，误差不停积累，导致IMF从高频到低频的发散程度越来越严重，甚至可能无法正确的提取出低频信号。如果信号的端点也是上、下包络线的端点，边界效应即可大大减轻。余弦窗窗函数在保证中心点附近有用信号的特征时，使得端点趋近于0，进而使得上下包络线收敛于端点，有效地抑制了边界发散现象。

为防止加窗改变原始信号，首先，采用波形特征匹配延拓方法，将信号延拓一定的数据长度。由于波形特征匹配延拓方法兼顾了原始极值点和非极值点数据，可以使得延拓数据与原始信号交界处的比较光滑，进而避免了加窗引起的原始频谱泄漏以及边界瞬时频率的跳跃。波形特征匹配延拓通过采用原始信号内部和边界处变化趋势最为相似的子波来对端点处数据进行延拓，是一种自适应的方法。在具体实现中，通过计算波形匹配来量化两端波形的变化趋势。

如图1所示，以左边界第一个极值点为极大值为例，mi、ni（n＝1，2，3，…）分别为曲线的极大值、极小值点，分别对应时间tmi、tni，a1为左端点，波形特征匹配延拓法以a1－m1－n1为边界特征波形，在全部数据中找到与a1－m1－n1构成的三角形最接近的波形为匹配波形，如ai－mi－ni，从ai的前一点（右边界为后一点）数据开始，向前（右边界向后）延拓波形数据，使延拓数据符合信号的自然走向。

图1 波形特征匹配原理图Fig.1 Diagram ofwave characteristicmatching

其次，为降低窗函数带来的误差，改进方法设计窗函数的宽度为可调。逐层提取IMF前，根据边界发散的程度，在信号两端加上可调的余弦窗函数，使得包络线沿着正确的方向延展，提高了IMF的分解精度。

可变余弦窗函数定义为：

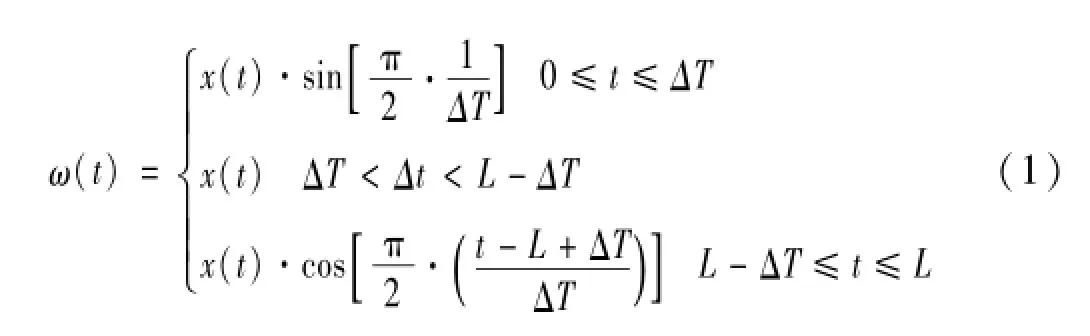
式中：L为信号延拓后的长度，ΔT为控制窗体中间部分时间范围的可变参数，它根据信号的改变而改变。由于边界发散程度是随着IMF的增加而不断增加的，根据筛选不同IMF前信号的发散程度而选取不同的值选取ΔT的大小。由图2可见，在窗函数的中部，其幅值等于1，而在窗函数的两端幅值逐渐衰减，直至窗函数的2个端点处幅值减至为0。宽度可调的余弦窗函数能够较准确地将延拓误差控制在信号两端，抑制边界的发散，实现算法的改进。

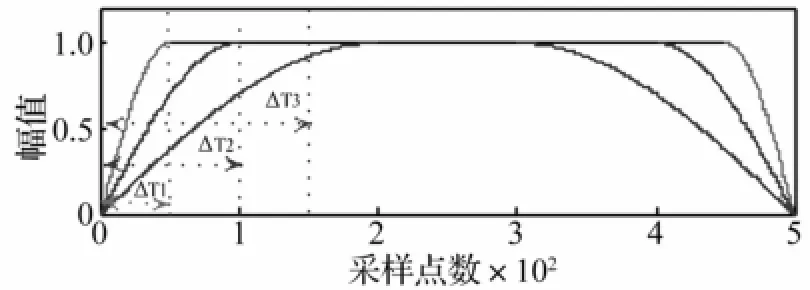
图2 可变余弦窗函数示意图Fig.2 Variable cosine window function diagram

基于延拓和可变余弦窗的EMD改进方法的步骤如下：

（1）对原始信号x（t）进行延拓，加一定ΔT的余弦窗ω（t）。将延拓信号x′（t）与余弦窗函数进行内积运算，得到信号y（t）＝［x′（t），ω（t）］，确定处理信号y（t）的所有极值点。

（2）求由局部极大值点和局部极小值点确定的上包络线和下包络线，Lmax（t）和Lmin（t）。

（3）计算包络线均值

a（t）＝（Lmax（t）＋Lmin（t））／2（2）

（4）求出h（t）＝y（t）－a（t）。

（5）如果h（t）不满足IMF条件，重复上面循环；如果h（t）是一个IMF，将信号f（t）＝x（t）－a（t）作为原始数据重复上面的循环，此时窗函数ΔT根据发散程度而改变。

当f（t）成为一个单调函数不能再从中提前出满足IMF条件的分量时，循环结束。这样就得到：

（6）对式（3）中的每一个本征模函数ci（t）作Hilbert变换，得到Hilbert谱及其边际谱。

2 端点效应的评价指标

（1）主观评价通过观察信号分解结果的发散程度，主观判断边界效应对于EMD结果的影响程度。

（2）相关系数对于仿真信号，一般有理论可以参照，边界效应的影响也容易评估。利用相关系数作为参数指标，可表征EMD分解结果与理想分解结果的接近程度，其基本原理如下［10］：

设a（n）、b（n）是两个能量有限的确定性信号，并假定它们是因果的，则定义

由上式可知，当a（n）＝b（n）时，rab＝1，则表明两个信号完全相关；当a（n）与b（n）完全不相关时，rab，当a（n）与b（n）有某种程度相似时，0＜｜rab｜＜1。因此，rab可以用来描述a（n）与b（n）之间的相似程度。

（3）能量角度边界效应会使IMF总能量会相应增加，因此可以比较EMD分解前后的能量来评估边界效应的影响程度。

原始信号和EMD得到的IMF的均方根有效值计算公式为：

式中：RMS为信号有效值，u（n）为信号序列，n为信号的采样点数。

定义评价指标θ

式中：RMSorginal原始信号有效值，RMSi为第i个IMF的有效值，n为IMF总个数。如果θ＝0，说明没有边界效应，θ值越大说明边界效应的影响越大。

3 仿真实验

仿真信号的表达式：

x（t）＝sin（2π×f1t）＋sin（2π×f2t）＋0.02sin（2π×f3t）（7）

式中：f1＝200 Hz，f2＝100 Hz，f3＝50 Hz，采样频率为2 000Hz。信号由三个正弦信号组成，低频信号比较微弱。仿真信号中由几个正弦谐波分量组成，呈现出一定的周期性。EMD分解过程实质是将信号不断平稳化的过程，最终将信号分解为满足一定条件的有限个IMF组，每一个IMF在局部吻合标准的正弦曲线，而且不同的IMF分量包含了不同的特征时间尺度。

如图3所示，分解时没有对原始数据进行任何处理。信号x（t）分解出来的3阶IMF都有一定程度的边界效应，而且边界发散程度逐渐增加，尤其是IMF3分量，已经无法表达出原信号中的低频小能量成分。

对原始信号进行延拓，如图4所示，对延拓后的信号进行EMD处理，得到图5，由图可以看出延拓后的数据仍然存在边界发散现象，尤其对于低频小能量的微弱信号尤为严重。将延拓信号x（t）与余弦窗函数进行内积运算，得到信号y（t）＝［x（t），ω（t）］。

图3 未处理的EMD分解结果图Fig.3 Untreated EMD decomposition resultsmap

图4 延拓后的信号Fig.4 Continuation signal

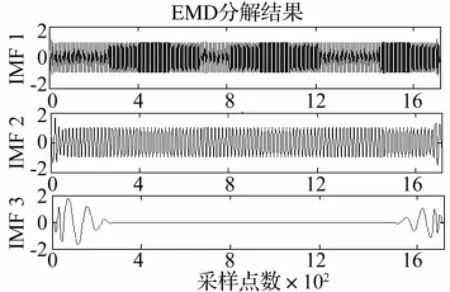
图5 延拓后的EMD分解Fig.5 The continuation EMD decomposition

图6为不同窗函数对应筛选不同IMF前的加窗结果，图6（a）中ΔT分别为43，80，110，逐层分解IMF前的加窗结果如图6（b）－（d）。从图中可以看出，信号两端的发散现象都得到了较好的抑制。图7为改进算法对信号x（t）分解截取有效数据与理想值的比较结果，由图中可以看出，3个IMF分量包括低频微弱信号被有效地分离出来，并且边界效应得到了很好的抑制。

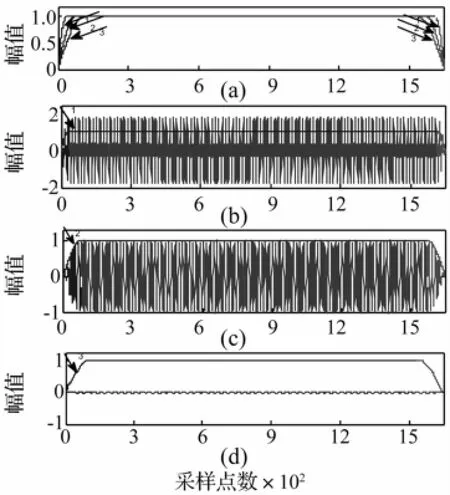
图6 窗函数和加窗结果Fig.6 Window function and window results

图7 改进算法的分解结果Fig.7 Decomposition results of improved algorithm

图8、9分别是信号x（t）未经过处理和用改进方法得到的Hilbert谱及其边际谱图。由图8可以看出，未处理的Hilbert谱在信号两端有比较严重的发散现象，而且发散程度从高频到低频逐渐增加，而通过本文方法处理后的Hilbert谱效果有明显的改善，同时低频分量的频率和幅值也显示出来。从图9中也能清楚地看到未经过处理的图像两端有很多离散的能量，而处理后的图像两端能量就相对集中，信号失真情况有明显改善。图9（a）中的幅值显示明显有很多微弱振荡，尤其是在低频部分出现了虚假成分。通过边界效应处理后得到的边界谱（b）中，幅值振荡基本消除，信号所包含的3个频率成分准确地显示出来。

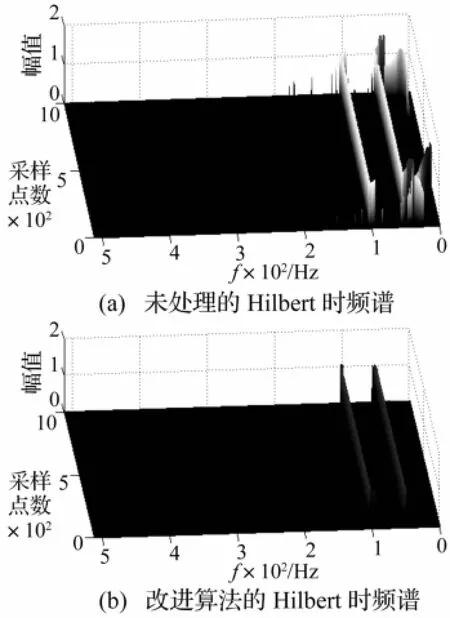
图8 三维Hilbert谱对比图Fig.8 Comparison of three dimensional Hilbert spectroscopy

图9 边际谱对比图Fig.9 Comparison ofmarginal spectrum

观察信号分解结果的的发散程度，可以看出改进的方法有效地抑制了边界发散现象。同时表1给出了未处理方法和改进算法的边界效应的性能评价，包括IMF分量与理想分量的相关性，以及EMD分解前后的能量对比参数θ值。相关系数r越接近于1，表明得到的结果越接近理想的分解结果。θ越小，表明虚假成分越少以及IMF分量的发散程度越小，边界效应的影响越小。从表1中可以看出未处理的EMD方法筛选出的IMF3与理想值基本上不相关，无法正确表达原信号中的低频小能量成分。而用改进算法的分解后，IMF1和IMF2与理想值的相关度提高，IMF3的rab也接近1，证明分解结果非常接近理想的分解结果，同时改进的算法使得θ值大大降低，说明边界效应减小，验证了改进算法的有效性。

表1 未处理的EMD算法以及改进算法的边界效应评价表Tab.1 Boundary effect evaluation of untreated EMD algorithm and an im proved algorithm

4 实例分析

将本文提出的EMD改进算法应用于横向裂纹故障信号的特征提取及诊断。由于裂纹故障信号包含信号的特征频率及其倍频成分，具有周期性，进而使得每个IMF分量趋近于正弦曲线，便于观察IMF的发散程度。另外，信号内部的周期性，使得本文提出的方法更具优势，这种规律使我们在寻找与边缘处波形相似的子波更加容易，减小了因为延拓产生的误差。图10是一个含横向裂纹故障转子的振动信号，转速为480 r／min。

图11是未处理算法分解结果，前3个分量中IMF1是噪声信号，IMF2、IMF3是含有裂纹故障特征的转子振动信号。从分解图中可以看出，分量两端存在发散现象，破坏了信号的规律性，并且随着分解层次的增加，发散现象越明显。

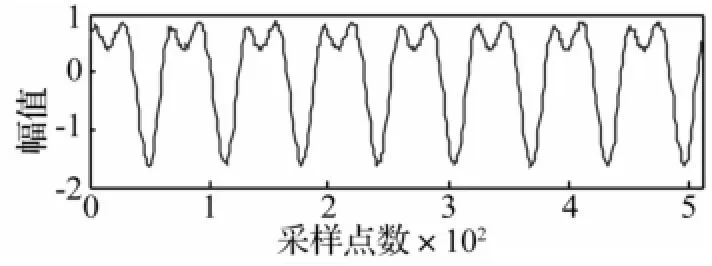
图10 转子裂纹的实际信号Fig.10 The actual signal of rotor crack

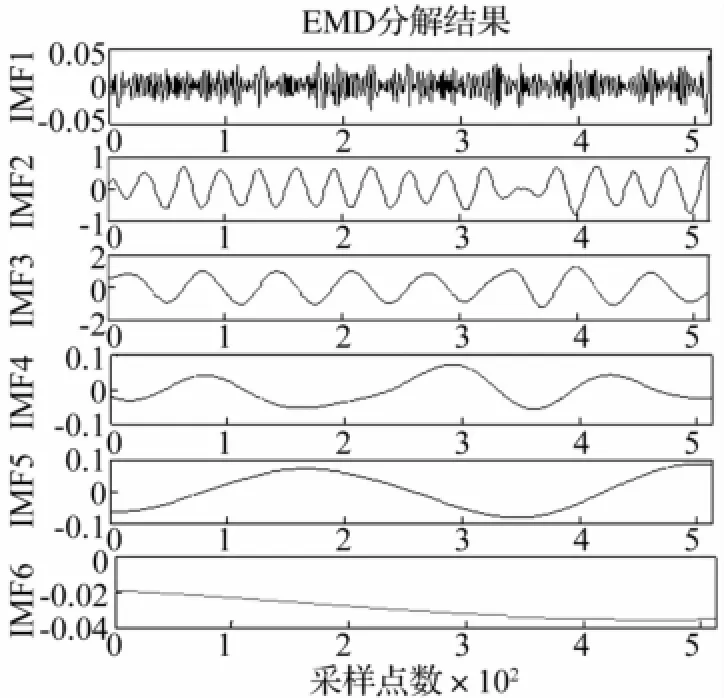
图11 未处理的EMD分解结果Fig.11 Untreated EMD decomposition results

根据观察IMF两端发散的程度，确定窗函数的宽度，使得信号的两端幅值逐渐衰减，直至归为0，进而抑制信号边界发散现象。图12是对原始信号延拓后，逐层提取IMF分量之前，加可调余弦窗的结果。图12（a）中窗函数的ΔT分别为43，53，63。图12（b）～（d）分别是所加的窗函数及加窗后效果。

图13为改进算法的分解结果，对比图11、图13可以看出，IMF2与IMF3的边界发散现象得到了很好的改善，各个分量的规律性也更明显。同时，从能量角度判定边界效应度的θ值由0.004 3减小为0.000 724，说明了改进算法的有效性。

图14为改进前后信号的Hilbert谱，图15为信号的Hilbert边际谱。比较图14，改进后的Hilbert谱的边界发散现象得到了抑制，信号的的能量也相对集中。比较图15，改进后的边际谱幅值微弱振荡基本消除，且2倍频分量得到了突出，其调频现象更加的突出。特征频率和2倍频的存在，是横向裂纹故障的特征，但是与不对中故障区分不明显。

图12 加可调余弦窗的结果Fig.12 Adjustable cosine window results

图13 改进算法的分解结果Fig.13 decomposition results of improved algorithm

图14 改进前后的Hilbert谱对比图Fig.14 Comparison of Hilbert spectrum before and after improvement

为进一步说明设备存在的是横向裂纹故障，采集一组高转速下的数据，转速为900 r／min。如图16所示，该组数据为单模态分量。图17为原始数据的Hilbert谱。可以看出较高转速下的轴频信号产生了频率调制，其调制频率与轴频相同，由此现象可作为转子横向裂纹故障的评判依据。根据以上分析，诊断该转子的故障为裂纹故障，同时验证了改进算法的有效性。

图15 改进前后的边际谱对比图Fig.15 Comparison ofmarginal spectrum before and after improvement

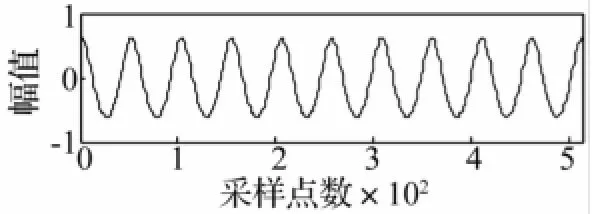
图16 高转速下的振动信号Fig.16 High speed vibration signal

图17 振动信号的Hilbert谱Fig.17 Hilbert spectrum of vibration signal

5 结 论

本文提出了一种延拓与可变余弦窗相结合的抑制经验模态分解边界效应的新方法。该方法先将信号延拓处理，根据信号的发散程度，逐层提取IMF之前，在信号两端加上宽度可变的余弦窗函数，使得包络线沿着正确的方向延展。由于窗函数的宽度设计为可以调节，使得每一个IMF分量边界发散问题最小化，降低了窗函数带来的误差，提高了IMF的分解精度。通过仿真实验改进算法与未经处理EMD算法的分解结果对比，可以看出改进算法使得边界效应得到了很好的抑制。另外利用边界效应性能评价指标分析了改进算法的分解结果，同样得出了改进算法抑制边界效应的有效性。EMD改进算法在故障信号特征提取中的应用实例，说明了改进方法能够有效地提取出故障信号的特征信息。

［1］Huang N E.The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proc Rsoc Lond A，1998，454：903－955.

［2］Shen Z J，Chen X F，Zhang X L，et al.A novel intelligent gear fault diagnosis model based on EMD and multi－class TSVM［J］.Measurement，2012，45：30－40.

［3］沈 路，周晓军，张志刚，等.Hilbert-Huang变换中的一种端点延拓方法［J］.振动与冲击，2009，28（8）：168－174.

SHEN Lu，ZHOU Xiao-jun，ZHANG Zhi-gang，et al.Hilbert-Huang an endpointextensionmethod［J］.Journal of Vibration and Shock，2009，28（8）：168－174.

［4］于慧君，陈章位，王庆丰.一种加窗重叠信号平滑连接方法及其在振动信号预处理中的应用［J］.振动与冲击，2007，26（8）：39－40

YU Hui-jun，CHEN Zhang-wei，WANG Qing-feng.A windowed overlapping signals smooth connection method and its application invibration signal preprocessing［J］.Journal of Vibration and Shock，2007，26（8）：39－40.

［5］韩建平，钱 炯，董小军.采用镜像延拓和RBF神经网络处理EMD中端点效应［J］.振动、测试与诊断，2010，30（4）：414－417.

HAN Jian-ping，QIAN Jiong，DONG Xiao-jun.Mirror extension and RBF neural network processing end effect of EMD［J］.Journal of Vibration，Measurement＆Diagnosis，2010，30（4）：414－417.

［6］胡劲松，杨世锡.EMD方法基于径向基神经网络预测的数据延拓与应用［J］.机械强度，2007，29（6）：894－899.

HU Jin-song，YANG Shi-xi.EMD method is based on the extension and application of radial basis function neura network forecast data［J］.Journal of Mechanical Strength，2007，29（6）：894－899.

［7］黄先祥，李胜朝，谢 建.新型经验模式分解端点效应消除方法［J］.机械工程学报，2008，44（9）：1－5.

HUANG Xian-xiang，LI Sheng-chao，XIE Jian.The new empirical mode decomposition endpoint effect elimination［J］.Chinese Journal of Mechanical Engineering，2008，44（9）：1－5.

［8］胡爱军，安连锁，唐贵基.Hilbert-Huang变换端点效应处理新方法［J］.机械工程学报，2008，44（4）：154－158.

HU Ai-jun，AN Lian-suo，TANG Gui-ji.Hilbert-Huang Transform endpoint effects processing new method［J］.Chinese Journal of Mechanical Engineering，2008，44（4）：154－158.

［9］程军圣，于德介，杨 宇.基于支持矢量回归机的Hilbert-Huang变换端点效应问题的处理方法［J］.机械工程学报，2006，42（4）：23－31

CHENG Jun-sheng YU De-jie YANG Yu.Processingmethod based on the Hilbert-Huang Transform，support vector regression machine end effects［J］.Chinese Journal of Mechanical Engineering，2006，42（4）：23－31.

［10］任达千，吴昭同，严拱标.EMD端点效应的评价指标及抑制边界效应的窗函数法［J］.制造业自动化，2007，29（1）：21－24.

REN Da-qian，WU Zhao-tong，YAN Gong-biao.Window functionmethod of evaluation of the end effect of EMD and suppress boundary effects［J］.Manufacturing Automation，2007，29（1）：21－24.

［11］Qi K Y，He Z J，Zi Y Y.Cosine window-based boundary processing method for EMD and its application in rubbing fault diagnosis［J］.Mechanical Systems and Signal Processing，2007，21：2750－2760.

［12］Parey A，PachoriR B.Variable cosinewindowing of intrinsic mode functions：Application to gear fault diagnosis［J］.Measurement，2012，45（3）：415－426.

Improved algorithm against end effect of EMD based on extension and variable cosine w indow

DING Xue-juan，SHIPei-ming
（College of Electrical Engineering，Yanshan University，Qinhuangdao 066004，China）

For the end effect of empirical mode decomposition（EMD）keeping pace with increase in filtering level，a new improved method using a combination of extension and variable cosine window was proposed.Firstly，the signalwas extended with a certain length of data.Then，the extended signal was processed at both ends with variable cosine window before extracting every intrinsicmodel function（IMF）tomake the end effect of each IMFminimized and to ensure the correct decomposition and the improvement of the EMD algorithm.Simulation analysis and crack fault diagnosis examples showed that the proposedmethod can inhibit end effects effectively.

signal processing；EMD；end effect；variable cosine window

TH165；TN911

A

国家自然科学基金（51005196）；高等学校博士学科点专项科研基金（20101333120004）

2013－01－17 修改稿收到日期：2013－03－23

丁雪娟女，硕士生，1986年生