非线性悬吊质量摆对输电塔减振控制的研究

侯 洁，霍林生，李宏男

（大连理工大学建设工程学部，大连 116024）

非线性悬吊质量摆对输电塔减振控制的研究

侯 洁，霍林生，李宏男

（大连理工大学建设工程学部，大连 116024）

针对悬吊质量摆减控制研究中小摆角线性分析的局限性，提出考虑悬吊质量摆大摆角非线性特性来计算结构体系动力响应的方法，将传统分析中的悬吊质量摆的线性刚度修正为非线性。以一输电塔为例，通过线性和非线性计算结果对比可知，当摆角过大时线性计算方法不满足线性小摆角条件，而非线性计算方法则可很好模拟质量摆在大摆角下的响应。通过参数分析讨论了正弦激励周期、摆长及质量比对输电塔减震率的影响。选取三条不同场地地震记录，计算输电塔附加质量摆体系的地震响应，结果表明在不同场地条件下，输电塔均具有明显的减震效果。

非线性响应；悬吊质量摆；输电塔；减震率

输电塔具有塔体高、柔性强等高耸塔体的特点，对地震和风等环境荷载的反应敏感，易产生较大的动力响应。对大跨度输电塔进行振动控制研究已成为电力工程与土木工程界的一个重要研究课题，既有其重要的理论意义，又有其重要的经济价值［1］。悬吊质量摆作为一种被动阻尼器，具有方法简便，易于实施，效果显著的特点［2］。

李宏男等［2－5］提出利用悬吊质量摆来减小结构地震反应的方法，导出了该种复合体系在地震动作用下的运动方程，利用实际地震记录进行了大量的数值计算，得出了一些对工程应用有参考价值的结果。康希良［6］论述了高层建筑结构利用悬吊质量摆减振的原理及减振性能的研究，通过分析得出了在高层建筑结构顶部各层设多个悬吊质量摆且其频率都和结构基频相同时，减振效果最好；质量摆的减振效果还随悬吊质量的增加而增加，但当悬吊质量与结构质量之比大于2%时减振效果增加较缓慢。邓洪洲等［7］利用悬吊质量摆对电视塔的风振控制进行研究，通过分析计算表明，悬吊质量摆对电视塔风振响应有很好的控制效果，并且设计安装简单方便、造价低，是一种实用性好的控制装置。贺业飞等［8］进行了悬挂质量摆对输电塔结构风振控制的全塔气动弹性模型试验，并基于控制减振机理和结构风振控制方程，采用脉动风速功率谱密度函数，利用三角级数法模拟了节点风速时程，计算了悬挂质量摆控制前后结构顺风向的加速度时程和均方根（RMS），进行了参数优化分析，研究结果表明，由模拟风载计算得到的塔顶RMS与试验结果吻合较好，悬吊质量摆模型可有效减小输电塔的风振响应。

悬吊质量摆在建筑结构的减振研究方面相对比较成熟，取得了一些成果［9－14］。但现有研究中通常将悬吊质量简单摆化为一个单摆振动系统，再按单摆小振幅运动得到单一的水平刚度系数，然后与主体结构模型建立整体的运动方程进行分析。这种简化方法的前提是将单摆振动时的控制力中的三角函数按泰勒函数展开，从而使得悬吊质量摆的运动方程得到简化。然而对于输电塔和悬吊质量摆体系而言，由于它们都具有柔性的特点，在外部荷载作用下，摆的振动幅度将明显偏离平衡位置。单摆振动的控制力中的三角函数不能简单的按泰勒函数展开，因此，在输电塔利用悬吊质量摆减振控制的研究中，必须考虑悬吊质量大振幅几何非线性的影响。然而，目前尚没有这方面的研究工作。因此，本文在现有研究成果的基础上，考虑悬吊质量摆大幅度几何非线性的对输电塔结构的位移响应的影响，提出了在非线性情况下摆和结构位移的精确算法。

1 非线悬吊质量摆

当悬吊质量摆放置在结构上时，我们重点关心单摆运动对结构产生的控制力，单摆与结构相联系的介质是绳索，因此单摆与结构的相互作用也只能通过绳索来传递。对于结构的振动而言，主要考虑水平方向的振动，因此绳索施加到结构上的力只有水平分量起到减振作用，通过对图1的单自由度体系分析可知，控制力为：

式中：mp为悬吊质量摆的质量，g为重力加速度，θ为摆转动的角度。

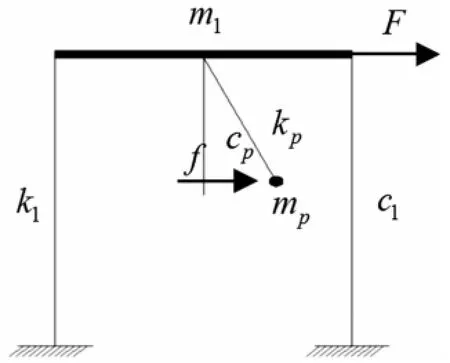
图1 结构示意图Fig.1 Schematic of structure with pendulum

同理，对于结构体系，运用D’Alembert原理，可得到结构的运动方程：

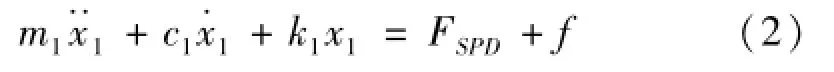
式中：m1，c1，k1，x1分别为结构的质量、阻尼、刚度和相对于地面的位移，f为外部干扰力（如风荷载）。

式（1）在满足线性小摆角的情况下，可得到cosθ≈1，sinθ≈θ；为了与结构的自由度相适应，摆自由度不取角度，而是采用水平位移x（x＝xp－x1，xp为摆相对于地面的位移），如图1中所示，x与θ之间的关系为：

θ≈x／l＝（xp－x1）／l（3）

式中，l为悬吊质量摆的长度。

摆的运动方程可转化与结构运动方程相类似的形式：

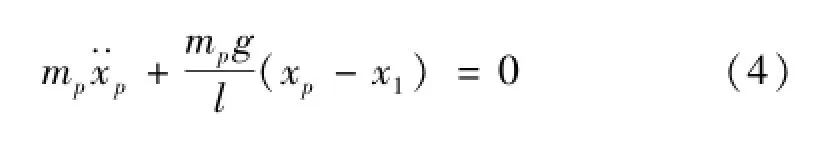
同样，控制力可以简化为：

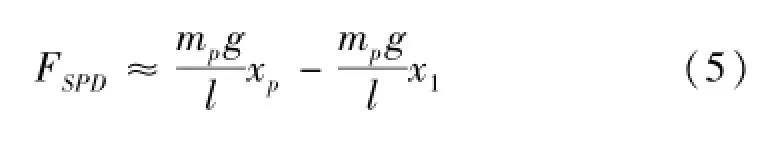
结构附加摆结构的运动方程为：

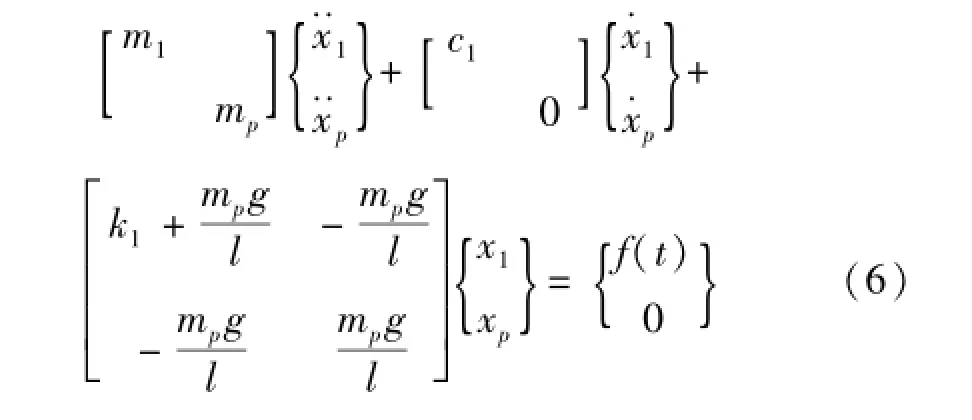
式（1）在大摆角的情况下，cosθ≈1，sinθ≈θ这两个式子显然不成立，应采用下面的精确分析。

2 线性与非线性结果对比

以一输电塔结构为例，对附加质量摆结构体系进行非线性分析。为简化计算将输电塔简化为23个节点，节点编号从上往下依次增大，三维有限元模型和简化后的结构体系示意图如图2所示。

为了得到精确的悬吊质量摆的各项参数以及线性和非线性结果的对比，根据实际情况，悬吊质量摆的参数设置如下：

（1）摆长l：可由悬吊质量摆与结构的周期之间的关系确定，即l＝g／（w／β）2；其中g为重力加速度，w为结构的一阶频率，β为悬吊质量摆与结构的周期之比，取0.8～2.4。

（2）质量比μ：质量比是悬吊质量摆的质量与结构的总质量的比值。

（3）周期比α：输入的正弦波的周期与结构周期的比，α取0.2～2.0。

（4）减震率γ：γ＝（D0－D1）／D0，D1和D0分别为加悬吊质量摆与不加悬吊质量摆时结构的最大位移。

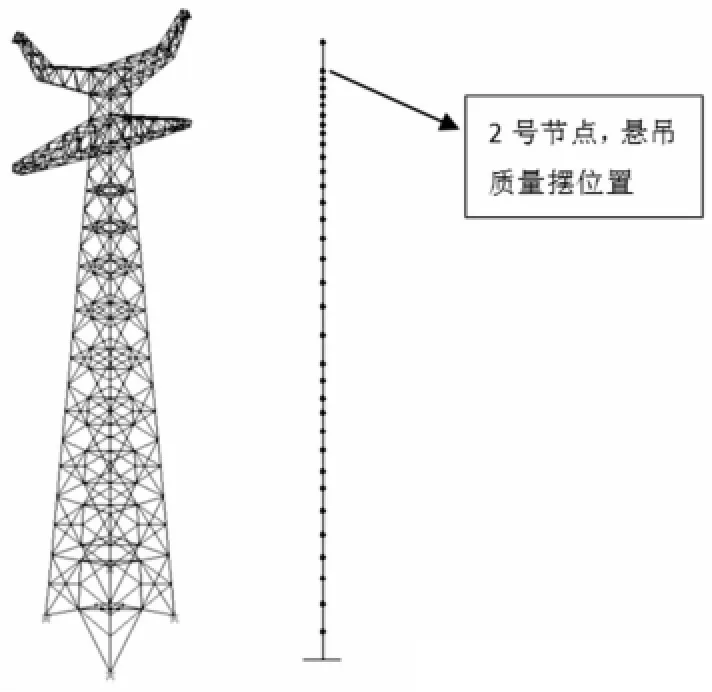
图2 三维有限元模型和简化后的输电塔结构体系Fig.2 Three dimensional finite elementmodel and simplified transmission tower structure system

图3为El Centro波（SW）作用下结构的顶层位移曲线（地震波的峰值加速度为0.2 g），在二号节点设置悬吊质量摆，以控制结构震动反应，取周期比β＝1，质量比μ＝0.03。图3为结构顶层位移时程曲线（取前30 s），图4为摆的转角时程曲线。

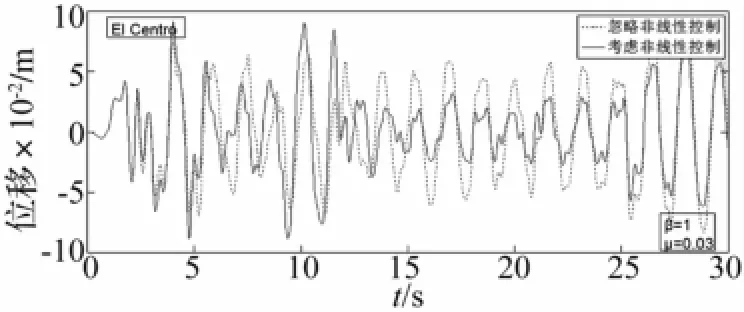
图3 结构的顶层位移曲线（El Centro）Fig.3 Time history of the displacement of top floor（El Centro）

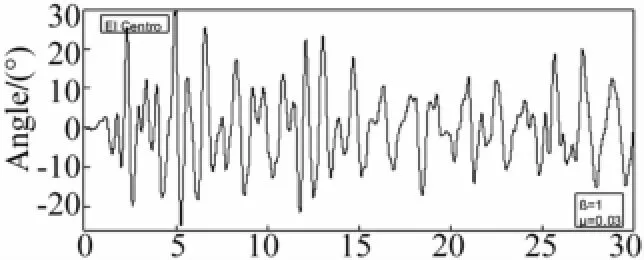
图4 摆的转角时程曲线（El Centro波）Fig.4 Time history of the angle of pendulum（El Centro）

由图3位移时程曲线可以看出，结构的反应，在整个地震作用时间内忽略非线性与考虑非线性控制的位移曲线有很明显的区别，顶层位移最大相差40%；图4的摆的角度时程曲线中转角的最大值接近于30°，远远超出了小振幅振动（θ＜5°）的限制条件，单摆小角度线性化的简化方法已经失效，因而现有的忽略非线性来计算结构的反应的方法存在极大的安全隐患。因此，在输电塔利用悬吊质量摆减震控制的研究中，必须考虑悬吊质量摆大幅度几何非线性的影响。

3 参数分析

当结构受到正弦激励Xg（t）＝a0×sin（w×t）时，用非线性的方法进行了大量的分析研究。图5、图6分别为质量比μ＝0.01与μ＝0.03时，悬吊质量摆与结构的周期比β、输入的正弦波的周期与结构的周期比α之间的关系曲线。当α在0.2～1.0之间时，结构的位移在β＝1附近时减震效果比较明显；α在1.2～2.0之间时，由于地基条件比较柔，输电塔结构本身也比较柔，在此种情况下，悬吊质量摆难以达到理想的减震效果。图7分别为α＝0.6及α＝0.8时在不同周期比β的条件下，减震率γ关于质量比μ的关系曲线。质量比μ越大，减震率越高；当μ＝0.01～0.03时，减震率增加的越快，并且较为经济合理，但超过0.04，减震率不再增长；β越小，摆长l越小，减震效果越显著。

4 不同场地条件下的验证

本文分别选取迁安波、taft波和天津波作为地震动输入（峰值加速度为0.1 g），以代表不同的场地类型。图8至图10分别表示质量比μ＝0.01、周期比β＝1.5时，在三条不同地震波作用下，结构的顶层位移曲线。表1至表3为由计算得到的结构未控、忽略非线性控制和考虑非线性控制三种情况时的最大位移、减震率、最大摆角、相对误差等参数。其中D0、Dx、Dn分别为结构未控、忽略非线性及考虑非线性控制三种情况结构顶层的最大位移反应；γx和γn为忽略非线性及考虑非线控制的减震率；θx和θn为忽略非线性及考虑非线性控制的最大摆角；η为相对误差，表示悬吊质量摆在忽略和考虑非线性时引起的摆的角度误差，其表达式如下：

由以上表1～表3和图8～图10可以看出，天津波作用在结构上，线性算法最大摆角可达到32°；Taft波作用时，线性算法最大摆角可达到14°，虽然考虑非线性和忽略非线性结构顶层的最大位移相差不大，但时程曲线相差较为明显，线性化的简化方法已经失效，现有的分析方法存在极大的安全隐患，因此必须考虑悬吊质量大振幅几何非线性的影响。迁安波作用时，最大摆角满足单摆小角度线性化的简化方法，考虑非线性与忽略非线性的结果基本一致，两条曲线基本重合，进一步验证了本文采用的计算方法的正确性。

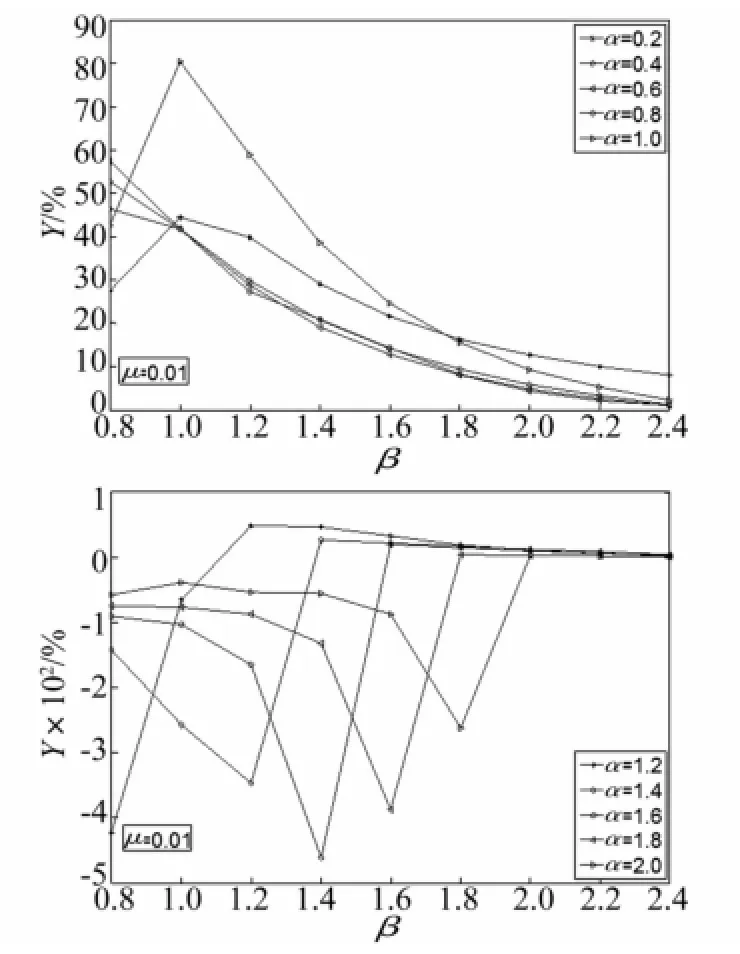
图5 减震率γ与周期比β的关系曲线（μ＝0.01）Fig.5 Curve of the relationship between decreasing amplitude ratioγ and period ratioβ（μ＝0.01）

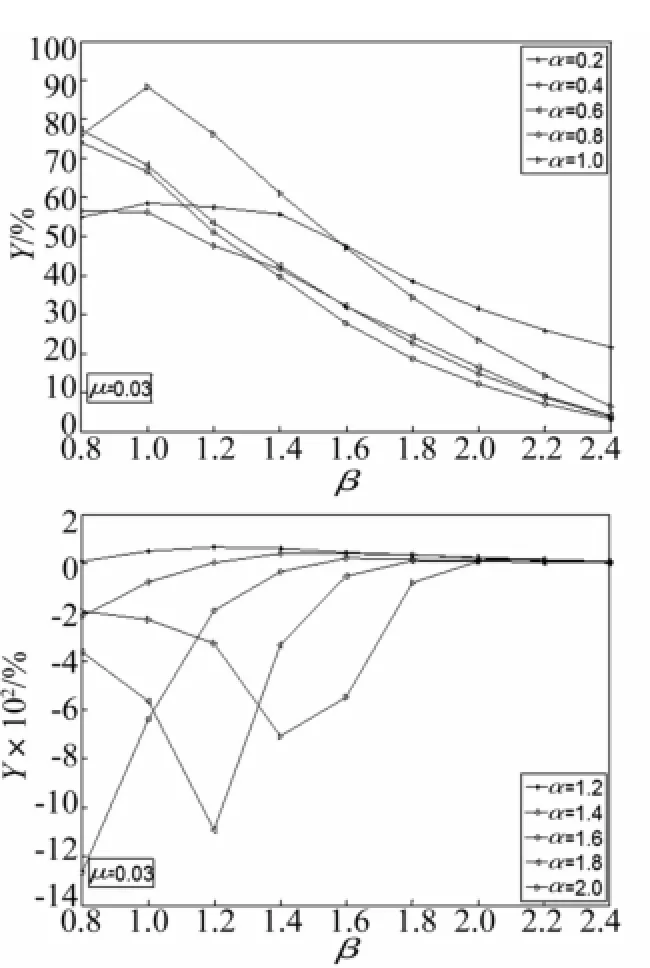
图6 减震率γ与周期比β的关系曲线（μ＝0.03）Fig.6 Curve of the relationship between decreasing amplitude ratio γand period ratioβ（μ＝0.03）

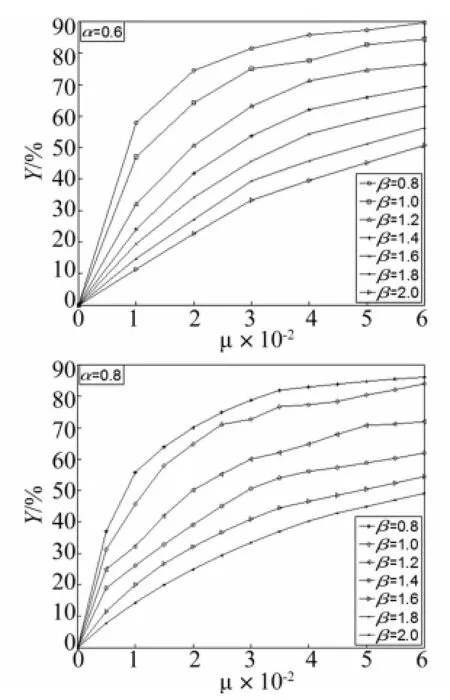
图7 减震率γ与质量比μ的关系曲线（α＝0.6，α＝0.8）Fig.7 Curve of the relationship between decreasing amp litude ratioγ and mass ratioμ（α＝0.6，α＝0.8）

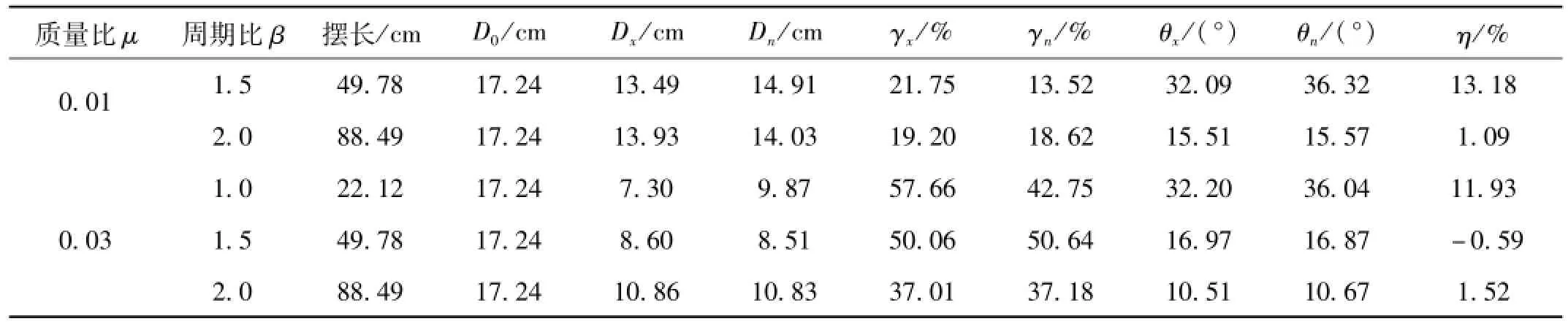
表1 最大位移响应（天津波（SN））Tab.1 Maximum disp lacem ent response（Tianjing（SN））

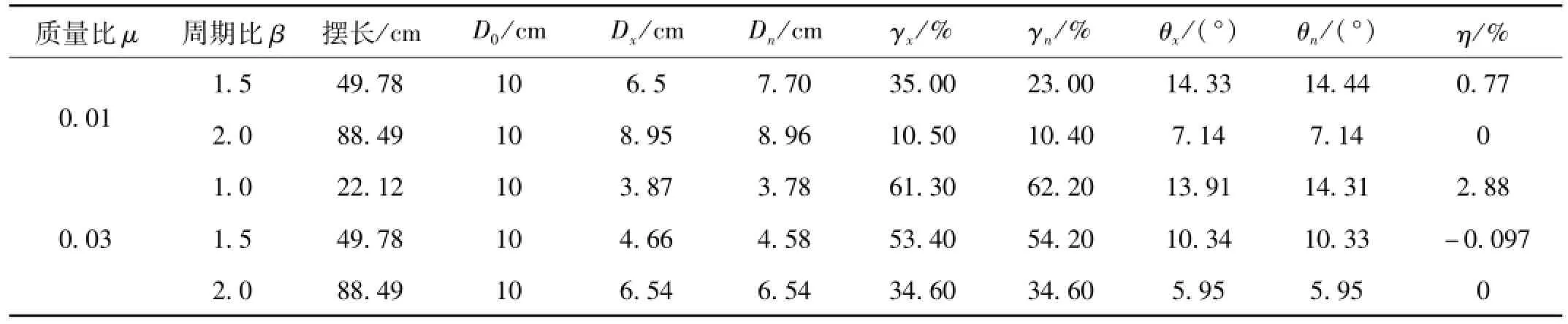
表2 最大位移响应（Taft波）Tab.2 Maximum displacement response（Taft）

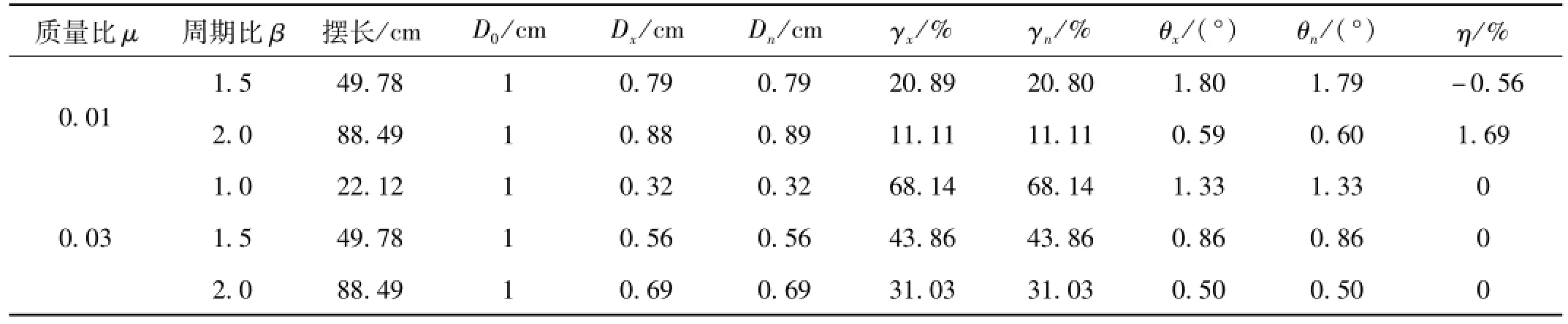
表3 最大位移响应（迁安波）Tab.3 Maximum d isp lacement response（Qian’an）

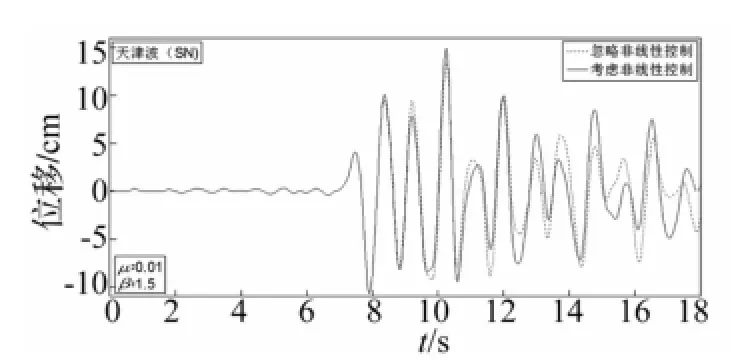
图8 结构的顶层位移曲线（天津波（SN））Fig.8 Time history of the displacement of top floor（Tianjing（SN））

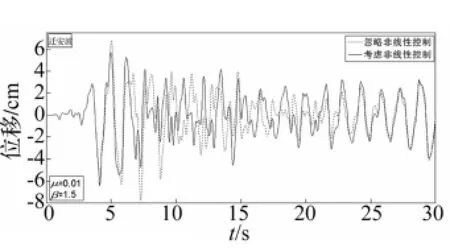
图9 结构的顶层位移曲线（Taft波）Fig.9 Time history of the displacement of top floor（Taft）

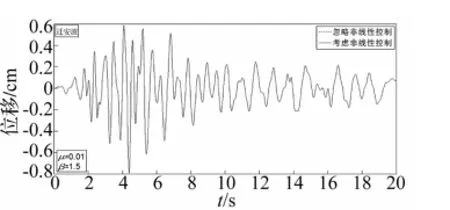
图10 结构的顶层位移曲线（迁安波）Fig.10 Time history of the displacement of top floor（Qian’an）

5 结 论

本文提出了利用悬吊质量摆减小结构地震反应分析的非线性分析方法。通过理论分析与数值计算，得到以下结论：

（1）应用悬吊质量摆，在周期比β较小时，摆长l较小时，悬吊质量摆的角度可能会超出单摆小角度线性化的适用范围，且减震率以及摆角误差较大，采用线性方法不能真实的反映结构的响应，应该采用非线性算法。

（2）一般情况下，周期比β在1附近时减震效果最好。当周期比β达到2时线性与非线性结果趋于一致，悬吊质量摆的角度也趋于符合线性摆的要求。

（3）场地条件相对较柔时，输电塔结构不宜采用悬吊质量摆来减震。

（4）其他条件相同的条件下，质量比μ越大减震效果越明显，且在质量比μ＝0.01～0.03时效果较好。

［1］李 黎，尹 鹏.大跨越输电塔－线体系风振控制研究［J］.工程力学，2008，12（25II）：213－229.

LI Li，YIN Peng.The research on wind-induced vibration control for big-span electrical transmission tower-line system［J］.Engineering Mechanics，2008，12（25II）：213－229.

［2］李宏男，Singh MP.结构动力吸振摆的优化参数［J］.世界地震工程，1994，11（4）：14－17.

LIHong-nan，Singh MP.Optimum parameters of vibration energy-dissipating pendulum for structures［J］.World Earthquake Engineering，1994，11（4）：14－17.

［3］李宏男.摆－结构体系减震性能研究［J］.工程力学，1996，13（3）：123－129.

LI Hong-nan.Study on vibration damping properties of pendulum-structure system［J］.Engineering Mechanics，1996，13（3）：123－129.

［4］李宏男，宋本有.高层建筑利用悬吊质量摆的减震研究［J］.地震工程与工程振动，1995，15（4）：55－60.

LIHong-nan，SONG Ben-you.Seismic respone reduction for tall buildings by suspended mass pendulums［J］.Earthquake Engineering and Engineering Vibration，1995，15（4）：55－60.

［5］李宏男，Singh MP，孙玉良.工程结构利用悬吊摆的振动控制［J］.地震工程与工程振动，1996，16（3）：61－71.

LI Hong-nan，Singh MP，SUN Yu-liang.Suspended pendulum damper for vibration control of engineering structures［J］.Earthquake Engineering and Engineering Vibration，1996，16（3）：61－71.

［6］康希良.高层建筑结构利用质量摆减震的分析［J］.兰州铁道学院学报，1996，15（4）：1－5.

KANG Xi-liang.Reductive vibration analysis of tall building structures using mass pendulums［J］.Journal of Lanzhou Railway Institute，1996，15（4）：1－5.

［7］邓洪洲，董 军，王肇民.多个悬吊摆体系对电视塔风振控制研究［J］.振动与冲击，1998，17（2）：39－42.

DENG Hong-zhou，Dong Jun，WANG Zhao-m in.Study on wind-induced vibration control of tv-tower with suspended mass pendulum system［J］.Journal of Vibration and Shock，1998，17（2）：39－42.

［8］贺业飞，楼文娟，孙炳楠，等.悬挂质量摆对大跨越输电塔的风振控制［J］.浙江大学学报，2005，39（12）：1891－1896.

HE Ye-fei，LOU Wen-juan，SUN Bing-nan，et al.Wind induced vibration control of long span transmission tower with suspended mass pendulums［J］.Journal of Zhejiang University，2005，39（12）：1891－1896.

［9］Guo AX，Xu Y L，LiH.Dynamic performance of cable-stayed bridge tower with multi-stage pendulum mass damper under wind excitations－Ⅰ：theory［J］.Earthquake Engineering and Engineering Vibration，2007，6（3）：295－306.

［10］Guo A X，Xu Y L，Li H.Dynamic performance of cablestayed bridge tower with multi-stage pendulum mass damper under wind excitations－Ⅱ：experiment［J］.Earthquake Engineering and Engineering Vibration，2007，6（4）：417－424.

［11］Nagarajaiah S，Pasala D T R.NEESR-Adapt-Struct：Semiactive control of ASD Device—Adaptive Length Pendulum Dampers［C］.19th Analysis＆Computation Specialty Conference，2010：325－334.

［12］Nagarajaiah S.Adaptive passive，semiactive，smart tuned mass dampers：identification and control using empiricalmode decomposition，Hilbert transform，and short-term Fourier transform［J］.Structural Control and Health Monitoring，2009，16：800－841.

［13］Roffel A J，Lourenco R，Narasimhan S，et al.Adaptive compensation for detuning in pendulum tuned mass dampers［J］.Journal of Structure Engineering，2011，137：242－251.

［14］Ben Mekki O，Bourquin F，Maceri F，et al.An adaptive pendulum for evolving structure［J］.Structure Control and Health Monitoring，2012，19：43－54.

Aseism ic control of transm ission towers w ith nonlinear suspended m ass pendu lum s

HOU Jie，HUO Lin-sheng，LIHong-nan
（Faculty of Infrastructure Engineering，Dalian University of Technology，Dalia 116024，China）

Due to the limitation of linear analysis for a suspended pendulum control system with small swing angle，a method analyzing dynamic response of a structure considering nonlinear stiffnessof pendulum was proposed here.Taking a 500 kV transmission tower as a numerical example and comparing the results under linear and nonlinear conditions，it was found that the swing angle of pendulum may exceed the limitation of linear assumption and the nonlinear analysis can simulate a structural dynamic system with large swing angles of pendulum perfectly.The effects of parameters of the control system including excitation periods，pendulum length and mass ratio on the seismic reduction ratio of the transmission tower were studied.Three seismic records were used to calculate the dynamic response of the transmission tower with suspended pendulums.The results showed that themitigation effect of suspended pendulums on the structural response is very obvious under different seismic excitations.

nonlinear response；suspended mass pendulum；transmission tower；seismic response reduction ratio

TU351.1

A

国家自然科学基金创新群体项目（51121005）；国家自然科学基金国际合作交流项目（51261120375）

2013－01－17 修改稿收到日期：2013－03－27

侯 洁女，硕士生，1988年生