定量表征纳米二氧化硅在聚合物基体中的分散性能研究

付 翔，王 靖，丁 娟，傅雅琴

（浙江理工大学先进纺织材料与制备技术教育部重点实验室，杭州310018）

定量表征纳米二氧化硅在聚合物基体中的分散性能研究

付 翔，王 靖，丁 娟，傅雅琴

（浙江理工大学先进纺织材料与制备技术教育部重点实验室，杭州310018）

为了能合理定量地评价粒子在基体中的分散性能，提出了一种定量表征颗粒在聚合物基体中分散状态的新方法，通过测量填充粒子的比表面积，来判断粒子在基体中的分散效果。该方法能够较全面地反映影响分散性的几个因素，如粒子尺寸、粒子浓度以及分布情况。利用该方法，对纳米SiO2/形状记忆聚氨脂复合材料的断面扫描电子显微镜的照片进行了分析，提取了一个分散指数。结果显示，对于比较难判断分散性的图片，可以用此量化方法判断分散性能。

纳米SiO2；形状记忆聚氨酯；图像处理；分散；定量

0 引 言

纳米SiO2是目前应用最广泛的纳米材料之一，它特有的表面效应、量子尺寸效应和体积效应等特性，使其与有机聚合物复合得到的纳米SiO2复合材料，不仅能发挥纳米SiO2自身的小尺寸效应、表面效应以及粒子的协同效应，而且又兼具有机材料本身的优点，这使得复合材料具有良好的机械、光、电和磁等功能特性，引起了国内外研究者的广泛关注［1-2］。

由于较强范德华力的存在，纳米SiO2颗粒在基体中易于团聚［3］。为了能得到优质的纳米SiO2聚合物复合材料，必须使纳米SiO2颗粒在聚合物基体分散均匀，使纳米SiO2复合材料性能获得大幅度提升。因此，合理评价纳米颗粒在基体中的分散性能就显得格外重要。它不但有助于深入了解材料的微观结构特征，而且有助于判断材料性能的优劣。目前经常被采用的表征方法主要是传统的物理学和材料学的定性表征手段或者利用纳米复合材料物性变化来间接表征纳米粒子分散状况。如采用透射电镜（TEM）、扫描电子显微镜（SEM）、X射线衍射等方法，对纳米复合材料的分散效果进行定性评定，或采用混合制备后的纳米复合材料热力学等性能进行评价，但这些方法均属于定性分析。

目前，对纳米颗粒分散性定量表征的研究并不是太多。Basu等［4］通过测量粒子之间的距离，并计算其平均值，以作为评判分散性好坏的标准。Diebold［5］则把每个颗粒作为参考点，分别计算其邻域内含有的粒子个数，如果含有的粒子少，分散性则相对较好。然而，这些计算方法都有一个共同的缺点，通过这些方法提取的指数并没有全面地涵盖影响纳米颗粒分散性的因素，如分布状态，粒子尺寸以及粒子浓度等。

因此，本文提出了一种新的计算方法，用于定量表征纳米SiO2颗粒分散状态。对材料的SEM断面图进行图像处理，如阈值化、膨胀腐蚀等，然后假定SiO2粒子为球体，求出平均比表面积，以此提取出一个合理可靠的指数，定量评价颗粒在基体中的分散性能。

1 实 验

1.1 实验材料

形状记忆聚氨酯（SMPU，日本Diaplex公司）；正硅酸乙酯（TEOS，天津市博迪化工有限公司）；N，N-二甲基甲酰胺（DMF，杭州高晶精细化工有限公司）；对甲基苯磺酸（PTSA，天津市博迪化工有限公司）。

1.2 试样制备与断面观察

采用溶胶-凝胶法［6］原位制备SiO2/SMPU复合材料，主要实验步骤如下：称取一定量的PTSA，溶解在DMF溶剂中，再将DMF溶剂倒入已称量的SMPU中，搅拌均匀，得到溶液A。再称取一定量的TEOS，在TEOS溶液中加入无水乙醇，混合均匀，得到溶液B。再将溶液B缓慢滴入溶液A中，搅拌2 h，得到澄清透明的溶胶。将得到的溶胶密封数天后进行干燥，即可得到分散均匀的浅黄色透明块状SMPU-silica杂化材料，并通过改变组分的含量，得到SiO2颗粒质量分数为4.5%，6%，10%的样品，分别标记为样品A、B、C；利用扫描电子显微镜对样品的断面进行观察。

2 分析方法

假设每个颗粒形状都是圆形，通过Matlab计算出它们各个面积S0，那么由此得出它们的等效半径R。公式如下：

由于表面能与粒子尺寸，粒子浓度和分布情况都有着密切联系。所以，通过比较每幅图像的粒子平均表面能，能更加客观地判断颗粒的分散状态。而且，表面能和比表面积是成正比的，因此，只要计算出每幅图像中颗粒的比表面积，就可以确切地反映出颗粒的分散状态。假设图像中的颗粒都为球体状，通过公式（1）计算出的等效半径，可以求得其等效球体体积V和等效表面积S，单位体积的物质所具有的表面积就是比表面积A。公式如下：

表面能可以理解为单位表面积上的能量，即发生单位面积变化时，外力所需要做的功，所以表面能越大，分散性越好。一定的物料，粉碎程度愈大，比表面积就越大，所具有的表面能就越高。因此比表面积越大，颗粒的分散程度越好［7］。

3 结果和讨论

在计算分散指数之前，需要对影响分散性的因素进行一些解释。首先是均匀分布，主要是从全局的角度去观察颗粒的分散性［8］。也就是说，图像中颗粒之间的距离是否都比较接近，是否出现团聚和凝聚。如果出现团聚现象，那么分布就是不均匀的。如图1所示。

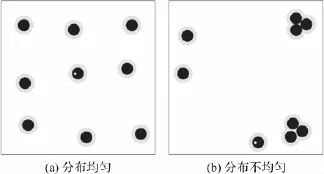
图1 颗粒分布示意

粒子浓度和粒子尺寸对分散程度的影响也是相当大，它是从局部的角度来反映其分散程度［8］。如图2所示，每幅图的分布状态都相同，图2（a）和（c）浓度相同，由于粒子尺寸的不同，其分散状态也呈现出不同，图（c）中粒子对基体作用的范围明显大于图（a），所以分散性也强于（a）。图2（a）和（b）粒子尺寸相同，但由于浓度不同，图（b）中粒子对基体作用的范围明显大于图（a），所以分散性也强于图（a）［9］。另外，粒子尺寸太大也不好，只有在某一范围内才对基体有加强作用。

然而，在真实的实验中，各个因素相互之间还有密切的联系，比如，随着粒子尺寸的减小，范德华力地逐步增强，发生团聚的概率会增大，分布也会更加不均匀［4］。当然，粒子浓度的变化也会对粒子尺寸和团聚发生的概率产生影响［10-11］。粒子尺寸对于表面能的影响较小，而对粒子团聚的影响更大，因为粒子尺寸一般都相差不大，而且当粒子尺寸小于某值时，就比较容易发生团聚。

笔者把上述提及的分析方法用在真实的SiO2/ SMPU的SEM图上。图3（a）是3个试样的扫描电子显微镜照片，（a）实例1中SiO2质量分数为4.5%，（a）实例2中SiO2质量分数为6%，（a）实例3中SiO2质量分数为10%。可以发现，从图中很难判断粒子在基体中分散性能的优劣，而且粒子尺寸和分布程度也很难一较高下。图3（b）为经过阈值化，膨胀腐蚀等处理后获得的图像。由于SEM图中有断面产生，阈值化过程中很难去除，因此当我们计算出白色区域的各个面积时，需要把断面层给剔除，防止其对指数正确性的影响。接着，按照第2部分中所描述的分析方法对其进行计算，求得每个颗粒的等效体积和表面积。最后，通过公式（2），计算出比表面积，即分散指数，获得的数值如图4所示。

图2 不同质量分数和尺寸颗粒的分布示意

图3 阈值化前后的图像

从图4可以发现，A试样的分散指数大于B试样，而B试样又大于C试样，这说明A试样的表面能大于B试样，而B试样又大于C试样。前文已讲述过，粒子团聚越多，也就是分布情况比较差，那么其表面能就会越小，分散性也会不好。

4 结 论

通过能量分布的规律，研究了一种把影响分散性的3个因素（粒子浓度、粒子尺寸，分布状态）涵盖在一个指数当中，定量表征纳米颗粒在聚合物基体中分散状态的新方法。并对3种分散性很难主观辨别的试样，进行了定量分析，获得分散指数，得到的指数与复合材料的常规理论有良好的相符性，显示出这个定量分析方法的适用性。

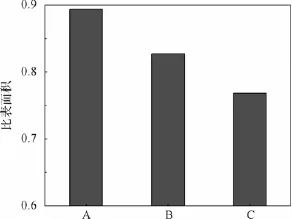
图4 不同质量分数的分散指数

［1］Gabrielson L，Edirisinghe M J.On the dispersion of fine ceramic powders in polymers［J］.Journal of Materials Science Letters，1996，15（13）：1105-1107.

［2］徐国财，张立德.纳米复合材料［M］.北京：化学工业出版社，2002，32-43.

［3］Reynaud E，Jouen T，Gauthier C，et al.Nanofillers in polymeric matrix：a study on silica reinforced PA6［J］. Polymer，2001，42（21）：8759-8768.

［4］Basu S K，Tewari A，Fasulo P D，et al.Transmission electron microscopy based direct mathematical quantifiers for dispersion in nanocomposites［J］.Applied Physics Letters，2007，91（5）：053105-053105-3.

［5］Diebold M P.Creative Advances in Coatings Technology［M］.Nurnberg：Nurnberg Congress，2005：101-116.

［6］Xu L B，Fu Y Q，Du M L.Investigation on structures and properties of shape memory polyurethane/silica nanocomposites［J］.Chinese Journal of Chemistry，2011，29（4）：703-710.

［7］闻荻江.复合材料原理［M］.武汉：武汉理工大学出版社，1998，22-23.

［8］Sul I H，Youn J R，Song Y S.Quantitative dispersion evaluation of carbon nanotubes using a new analysis protocol［J］.Carbon，2011，49（4）：1473-1478.

［9］Khare H S，Burris D L.A quantitative method for measuring nanocomposite dispersion［J］.Polymer，2010，51（3）：719-729.

［10］Singh R P，Zhang M，Chan D.Toughening of a brittle thermosetting polymer：effects of reinforcement particle size and volume fraction［J］.Journal of Materials Science，2002，37（4）：781-788.

［11］Thostenson E T，Li C Y，Chou T W.Nanocomposites in context［J］.Composites Science and Technology，2005，65（3）：491-516.

Quantitative Characterization of Dispersing Performance of Nano SiIicon Dioxidein PoIymer Matrix

FU Xiang，WANG Jing，DING Juan，FU Ya-qin
（Key Laboratory of Advanced Textile Materials and Manufacturing Technology，Ministry of Education，Zhejiang Sci-Tech University，Hangzhou 310018，China）

To rationally and quantitatively evaluate dispersing performance of particles in the matrix，this paper puts forward a new method for quantitative characterization of the disperse state of particle in the polymer matrix.The dispersing effect of particles in the matrix is judged through measuring specific surface area of the filler particles.This method can comprehensively reflect the factors influencing the dispersity，such as particle size particle concentration and distribution.This method is used to analyze the pictures of the section of nano SiO2/shape memory polyurethane compositetaken by the scanning electron microscopy and extract a dispersion index.The result shows that the dispersing performance can be judged through this quantitative method for the pictures which are difficult to judge the dispersion.

nano SiO2；shape memory polyurethane；image processing；dispersion；quantification

O612.4

A

（责任编辑：王宁宁）

1673-3851（2014）02-0175-04

2013-05-15

付 翔（1988-），男，浙江德清人，硕士研究生，主要从事高分子纳米复合材料研究。

傅雅琴，E-mail：fyq01@zstu.edu.cn