基于比等效热阻法的片状填料填充聚合物复合材料的导热性的预测
2014-05-25朱凤博张顺花
朱凤博,张顺花
(浙江理工大学先进纺织材料与制备技术教育部重点实验室,杭州310018)
基于比等效热阻法的片状填料填充聚合物复合材料的导热性的预测
朱凤博,张顺花
(浙江理工大学先进纺织材料与制备技术教育部重点实验室,杭州310018)
基于比等效热阻法建立了简化了的片状填料填充聚合物基复合材料的导热模型并推导出了相应的等效导热系数公式。以云母片填充聚乳酸为例,应用有限元软件ANSYS建立了云母体积分数在11%下的聚乳酸/云母复合材料的三维稳态热传导单元模型,并模拟了热流沿云母片厚度方向和径向传递的过程。结果表明,当热流沿云母片轴向方向上流动时,经ANSYS模拟求得的复合材料的等效导热系数和文中推导的公式的所给出的预测值更为接近;当热流沿云母片的径向流动时,随着云母体积分数的增加,复合材料的等效导热系数的预测值呈指数性增长,并且高于ANSYS的计算结果。有限元结果和本文的公式均表明,片状填料填充聚合物复合材料的等效导热系数可分解为是沿热流不同正方向上的贡献,更长的等效导热路径使片状颗粒在填充聚合物后能提供更为出色的导热性能。
聚合物基复合材料;片状填料;导热系数;有限元模拟;比等效热阻法
0 引 言
传统导热材料多为金属和金属氧化物及其他非金属材料,随着工业生产的进步,人们也对导热材料的综合性能提出了更高要求,如轻质、耐化学腐蚀性强、电绝缘性优异等。导热绝缘聚合物基复合材料由于其结合了上述优点而越来越受到关注。纯聚合物导热系数很低,利用导热系数高的无机粒子填充聚合物可以有效改善聚合物基体的热性能[1-3]。对于这类功能型复合材料,其等效导热系数是表征其导热能力的最重要的参数,因此对等效导热系数定量的预测以及复合材料导热原理的研究对复合材料的设计和制备具有重要意义[4-6]。
目前大部分对导热聚合物基复合材料的等效导热系数预测是基于填充颗粒是球形粒子这一基本原则来研究填充体积分数与等效导热系数的关系[7-11]。而在实际的复合材料的制备中,高比表面积的片状填料也有较大的使用比例,片状填料分布在聚合物基体中更有利于导热性能的提高[3,12-14]。因此,如何对片状填料填充聚合物基复合材料建立体积分数与等效导热的相关性模型,对于优化片状复合材料的导热性能具有非常重要的意义。
在较早时候,Hatta基于等效夹杂理论推导了具有大的径厚比的片状颗粒填充聚合物复合材料的等效导热系数的公式,并以片状的氮化硼(BN)颗粒填充Kerimid树脂为例,对比了等效导热系数的理论值和实测结果,发现该复合材料的导热系数的实测结果明显高于其理论值,Hatta解释为是在测试过程中树脂基体与BN发生了某些反应而导致理论值出现偏差[14],但是从其模型中并不能很好解释片状颗粒在填充聚合物时所拥有的这种优异的填充效果。近年来,比等效热阻法由于其具有简单且不考虑填料间的相互作用的优势而较多地应用于对低填充量的聚合物复合材料的导热系数的估算,并且已经在球形颗粒填充的聚合物复合材料的热性能的分析中取得较好的效果[7-11],但将这种方法应用于片状颗粒填充的复合材料的导热性的分析的研究并不多见,因此,本文基于比等效热阻法建立片状的颗粒填充聚合物的传热模型,推导了相应的复合材料的等效导热系数公式,再以导热系数相对较高的云母共混导热性很差的聚乳酸为例,利用有限元分析软件ANSYS对该复合材料体系的传热过程进行三维的有限元模拟,探讨片状颗粒填充聚合物复合材料的导热过程,以期为高导热聚合物复合材料的设计和制备提供一定理论依据。
1 导热模型的构建与等效导热系数的推导
1.1 基于比等效热阻法的片状颗粒填充聚合物复合材料的导热模型
根据比等效热阻法的基本思想,只要所选取的复合材料的单元体与总体有相等的比等效热阻,则不论单元体尺寸大小,在只考虑热传递时,这种单元体与复合材料总体的等效导热系数相等。对于颗粒填充聚合物复合材料,填料填充量一般不会很高,否则会由于颗粒的团聚而影响基体的性能,且颗粒在高聚物基体中均匀良好的分散是制备高性能复合材料的基础,基于上述两点,认为颗粒之间无相互作用且分散均匀,因此通过比等效热阻法,可以将复合材料考虑为由一系列微小立方体单元连接而成,每个基本的单元由基体材料仅包含着一个分散相的片状颗粒。那么片状颗粒填充聚合物复合材料的等效导热系数的计算的问题可以简化为计算具有相同比等效热阻的立方体单元体的导热系数。根据片状颗粒的形状特点,可将其简化为直径为d,厚度为t的短圆柱[15-16],取导一个立方体单元分析,热流从正方体的上面进入,热量沿短圆柱轴向传递,如图1所示。
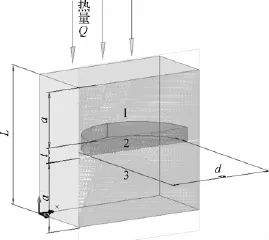
图1 热传递过程的单元分析
由于聚合物复合材料的热成型过程一般是在熔融下成型的,认为填料被聚合物基体很好地包裹起来,并且填料未经过有机改性,因此不考虑界面热阻。如图1所示,将所选取的热传递过程的单元体划分为3部分,其中第1、3部分只由连续相基体组成,第2部分由基体和片状颗粒共同组成,假设热量沿短圆柱的径向方向传递。根据热阻串联[7],将3部分的热阻相加就可以得到整个单元的等效热阻,然后根据热阻的定义求出单元的等效导热系数。
设K1,K2,K3分别为3部分的平均导热系数,Kf,Km,分别为粒子和基体和的导热系数;Af,Am,分别是无机粒子和聚合物基体截面的面积;Qf,Qm,分别是通过无机粒子聚合物基体截面的热量。
对于第1、3部分:K1=K3=Km,则,根据热阻的定义,第1、3部分的热阻为:
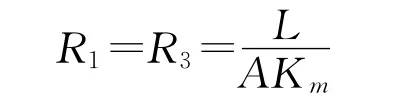
对于第2部分:利用微分的方法,取厚度微元为d y的薄片,该薄片的导热系数为K2′则,单位时间内通过薄片的总热量为:
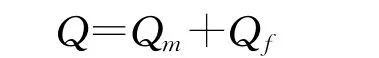
其中,
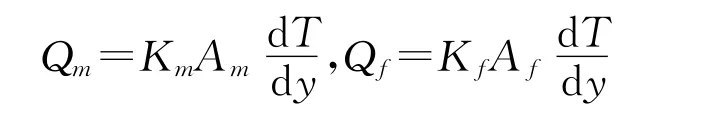
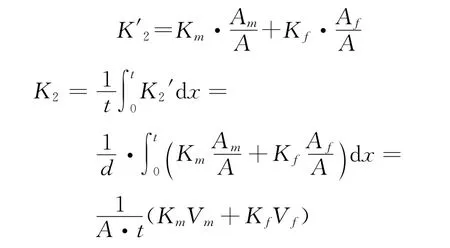
因此,第二部分的热阻为:
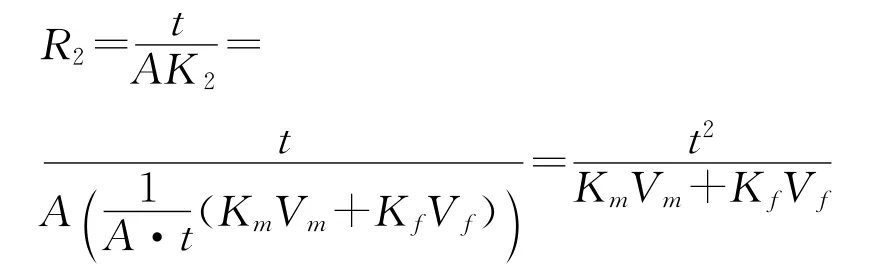
其中,Vm,Vf分别为单元第2部分中基体和分散相的体积。
总热阻为
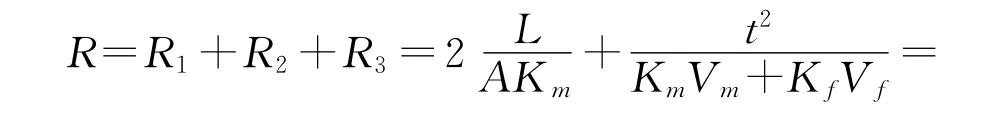

其中Ke为总的等效热导率,则
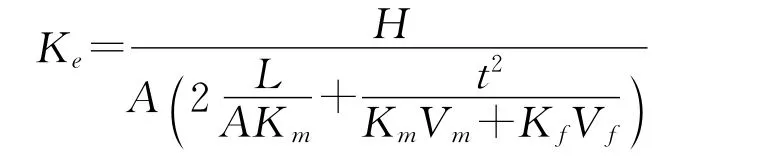
作为对比,给出较早开始研究Hatta[14]所推导的片层颗粒填充时的等效导热系数公式:
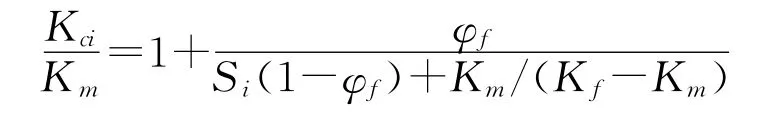
其中,i为热传导方向,i=z时,热量沿填料轴向传递,i=xy时,热量沿填料径向传递,且:
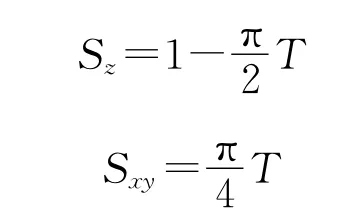
其中,T为填料的径厚比。
1.2 等效导热系数估算
以聚乳酸(PLA)树脂为基体,导热系数Km= 0.025 W/(m·K);填料为片状云母颗粒(Mica),导热系数Kf=0.58 W/(m·K)[17],代入(2)式,计算出不同填充体积分数,热量沿云母片轴向传递时,PLA/Mica复合材料的等效导热系数的估算值;作为对比,同时将PLA和云母的的导热系数代入到Hatta模型中,计算出由Hatta模型得到的不同填充体积分数时的等效导热系数估算值。
1.3 有限元模拟
1.3.1 基本假设
近年来,对于复合材料的导热的模拟,相当普遍的一种方法是建立近似于真实材料中填料分布情况的代表体元(RVE),这种方法能够在最大程度上模拟真实材料的结构,但是实际上在应用时较为复杂。因此若仅建立复合材料的单胞模型并模拟其导热情况,仍然能将复杂问题简单化。因此,假设云母为尺寸一致、质地均匀且各向同性的短圆柱形的片状颗粒;云母粒子之间没有接触,并且在基体中分布均匀,因此,取由单个云母片及其外面包覆的高分子基体组成的导热单元分析。
1.3.2 热传导有限元模型的建立
根据云母在PLA中的体积分数,以及考虑云母的径厚比,算出单元体的边长,使用ANSYS建立复合材料单元的三维模型(图2)。采用自动划分网格工具,鉴于云母片为短圆柱形,因此采用四面体单元比采用六面体单元能够更容易地表示具有圆形几何形状的物体。在单元体正面施加温度约束为35℃;后面施加对流换热系数为25 W/(m2·K)的空气对流载荷,环境温度取为25℃。其他四面施加绝热边界条件[9]。
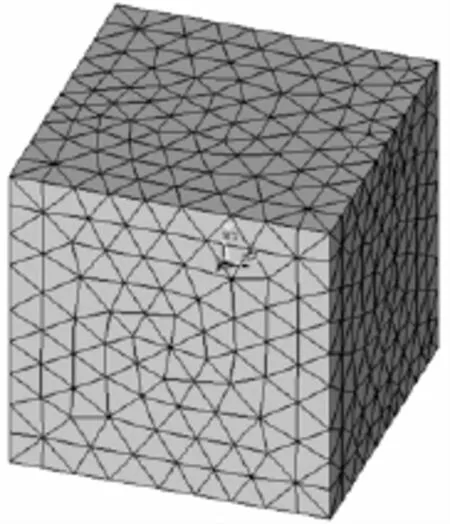
图2 颗粒填充高分子复合材料传热简化模型
2 结果与讨论
2.1 温度云图
图3为聚乳酸及其云母复合材料热传导单元的温度云图,其中,云母的填充体积分数为5.45%。图3(a)为纯聚乳酸单元截取一半之后的温度云图的右视图,图3(b),(c)则反映出热流沿不同方向进入时,PLA/Mica复合材料导热单元内的温度变化情况。在纯PLA单元中,温度是均匀变化的;相反,在PLA/Mica单元中,在云母的周围,温度变化的速度较聚乳酸基体要慢很多。相比较而言,云母导热系数比聚乳酸基体大很多,根据最小热阻力法则,热流会沿着热阻最小的方向流动,热流在靠近云母附近受到的热阻更小,温度变化也就更为缓慢。从图3中还可看出,等温线在云母的周围发生强烈的改变,尤其是当热量沿云母片的径向传递时,这种现象尤其明显。这是由于云母这类具有片层结构的填料在不同方向上导热路径不同,相应的在不同方向上等温线变化的程度也不同。

图3 PLA/Mica复合材料的传热温度云图
2.2 热流矢量云图
图4为单元内的热流矢量图,反映了单元中热流流动的方向及大小。图中箭头指向了热流的方向,颜色深浅表示热流的强弱。从图4可以看出,在热流刚进入模型时,热流分布是较为均匀的;而在云母的周围,热流密度增加。可以认为,在热传递的过程中,具有大的比表面积和高的导热系数的云母片扮演了类似于“散热板”(heat sink)的角色,加速了热量的传递。由于云母片的导热率比聚乳酸基体大很多,根据最小热阻力原理,热流会沿着热阻最小的方向流动。因此热流汇集并在云母粒子附近热流密度达到峰值,当热量沿着云母径向传递时,这种差异尤其明显,通过云母的热流量几乎是聚乳酸基体的25倍。这是由于云母这类片状填料具有很高的径厚比,热量沿云母片的径向方向流动时,通过的导热路径更长,热流变化更为明显。
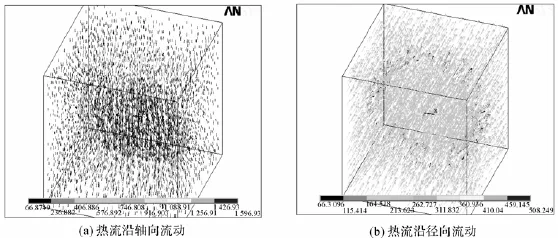
图4 PLA/Mica复合材料的传热温度云图
2.3 等效导热系数
图5是云母体积分数分别为2.33%、3.64%、4.56%、5.45%、7.27%、9.09%、10.91%时复合材料导热系数的模拟值和本文中所推导的公式以及由Hatta模型所计算出的结果的对比,如图5所示。
由图5可以看出,当沿云母片的轴向方向测量时,由ANSYS模拟求得的复合材料导热系数随填料含量的增加几乎呈线性增加,与文中的公式(2)所计算出的等效导热系数的结果是非常吻合的,而Hatta模型的结果则偏离ANSYS的结果很多。当沿云母的径向测量时,等效导热系数则表现出完全不同的增长趋势,尤其是在云母体积分数超过6%时,由本文中的公式所计算出的等效导热系数的值不仅高于Hatta公式和有限元模拟计算的结果,而
且几乎呈指数增长,这种趋势在很多文献的实验中已经被证实[3-4,13-14,18]。复合材料的导热系数在不同方向上所表现的出的巨大差别,也能由本文推导的公式中反映出:本质上来看,在热流流动方向的导热路径的长度是决定复合材料等效导热系数的决定性参数,片状填料具有很高的径厚比,因而热流沿填料的径向流动时其有效导热路径的长度远大于其厚度方向的导热路径的长度,因此其等效导热系数不仅比厚度方向测量的更大,而且随着体积分数的增加提高也更快。因此,对于任何形状填料填充聚合物的复合材料,其等效导热系数都可分解为由填料在不同的热流流动正方向上的贡献,但相比在各向方向上具有相等的等效导热路径长度的球形颗粒和方形颗粒而言,当填充含量相等时,具有高的径厚比的片状填料显然在其径向正方向上具有更长的导热路径,而且填料在一般成型条件下无规则取向,因此片状填料容易在各个方向上都有相当可观的导热路径,并表现出更为优异的导热性。
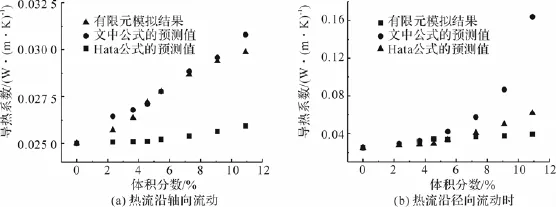
图5 PLA/Mica复合材料等效导热系数的理论计算值与模拟值
尽管本文的模型是建立在片状颗粒在基体中整齐排列并且无相互作用的假设之上的,但是仍然提供了解释片状填料在提高复合材料导热性能方面比球形或方形颗粒更为出色的原因;另一方面,经过分解后的公式也对以后制备高导热性的复合材料提供了建议,比如,把填料制成具有高的径厚比的片状或短纤维状,或者在我们需要高导热性的方向上,使片状填料尽量按径向取向排列以增加填料在传热方向上的尺寸等。考虑到本文所做的假设,对于填料的尺寸分布,取向以及有机改性后的填料与聚合物基体之间可能存在界面热阻等因素对于复合材料导热性的影响则有待进一步探讨。
3 结 论
a)基于比等效热阻法建立了片状填料填充聚合物基复合材料的导热模型并推导出了相应的预测等效导热系数的公式,可适用于描述较低体积分数下片状填料填充聚合物材料的传热过程。
b)以云母填充聚乳酸为例,应用ANSYS软件建立了低填充量(填料体积分数<11%)的PLA/ Mica复合材料的三维热传导单元模型,并模拟了热量沿云母厚度方向和径向传递的热过程。结果表明,当热流沿云母片轴向流动时,经ANSYS模拟求得的复合材料的导热系数和本文推导的公式所得到的预测值较为接近,且都随云母体积分数的增加而提高,而当热流沿云母片径向方向流动时,复合材料的等效导热系数随云母体积分数的增加几乎呈指数性增长。
c)片状颗粒填充聚合物复合材料的导热性可认为是由填料在不同热流正方向上的贡献,更长的等效导热路径使片状颗粒在填充聚合物后能提供更为出色的导热性能。
[1]董其伍,刘琳琳,刘敏珊.预测聚合物基复合材料导热系数方法研究进展[J].材料工程,2009(3):78-81.
[2]费海燕,朱 鹏,宋艳江,等.石墨和炭纤维分别改性热塑性聚酰亚胺复合材料的导热行为[J].复合材料学报,2007,24(5):44-49.
[3]Tekce H S,Kumlutas D,Tavman I H.Effect of particle shape on thermal conductivity of copper reinforced polymer composites[J].Reinforced Plastic&Composites,2007,26(1):113-121.
[4]Zhou W,Qi S,An Q,et al.Thermal conductivity of boron nitride reinforced polyethylene composites[J]. Material Research Bulletin,2007,42(10):1863-1873.
[5]Ott H J.Thermal conductivity of composite materials[J].Plastics and Rubber Processing and Applications,1981,1(5):9-24.
[6]Wang J J,Su Y X.Effects of interfacial thermal barrier resistance and particle shape and size on the thermal con-ductivity of AIN/PI composites[J].Composites Science and Technology,2004,64(10/11):1623-1628.
[7]梁基照,刘冠生.无机粒子填充聚合物复合材料传热模型及有限元模拟[J].特种橡胶制品,2006,27(6):35-38.
[8]梁基照,刘冠生.颗粒填充聚合物复合材料导热系数公式的初步验证[J].塑料科技,2007,35(7):30-32.
[9]Liang J Z,Li F H.Simulation of heat transfer in hollow-glass-bead-filled polypropylene composites by finite element method[J].Polymer Testing,2007,26(3):419-424.
[10]刘祥宽,Mehari S,胡献国.球形颗粒填充聚合物基复合材料有效导热系数的研究[C]//第8届全国摩擦学大会论文集,2007:217-222.
[11]宋思洪,廖强,沈卫东.不同形状颗粒弥散复合材料的等效导热系数[J].重庆大学学报,2011,34(6):87-91.
[12]虞锦洪.高导热聚合物基复合材料的制备与性能研究[D].上海:上海交通大学,2012.
[13]Kim W J,Taya M,Nguyen M N.Electrical and thermal conductivities of a silver flake/thermosetting polymer matrix composite[J].Mechanics of Materials,2009,41(10):1116-1124.
[14]Hatta H,Taya M.Thermal diffusivities of composites with various types of filler[J].Journal of Composite Materials,1992,26(5):612-625.
[15]Mortazavi B,Hassouna F,Laachachi A,et al.Experimental and multiscale modeling of thermal conductivity and elastic properties of PLA/expanded graphite polymer nanocomposites[J].Thermochimica Acta,2012,552(10):106-113.
[16]Mortazavi B,Baniassadi M,Bardon J,et al.Modeling of two-phase random composite materials by finite element,Mori-Tanaka and strong contrast methods[J]. Composites Part B:Engineering,2012,45(1):1117-1125.
[17]杨世铭,陶文铨.传热学[M].北京:高等教育出版社,1998.
[18]KumlutaşD,Tavman I H,Turhan Coban M.Thermal conductivity of particle filled polyethylene composite materials[J].Composites Science and Technology,2003,63(1):113-117.
ThermaI Conductivity Property of FIake FiIIers Reinforced PoIymer Composites Based on EquivaIent ThermaI Resistance
ZHU Feng-bo,ZHANGShun-hua
(Key Laboratory of Advanced Textile Materials and Manufacturing Technology,Ministry of Education,Zhejiang Sci-Tech University,Hangzhou 310018,China)
In this paper,a simplified thermal equivalent model of the flake filler reinforced composite was established based on equivalent thermal resistance and corresponding equivalent thermal conductivity coefficient formula is derived.Take the mica plate used to fill polylactic acid for example.A three-dimension steady-state thermal conduction unit model for polylactic acid/mica composite is made through ANSYS software with mica volume fraction of 11%.The process of thermal flux transferring to thickness direction and radial direction of the mica plate is simulated.The results show that when thermal flux flowed along the axial direction of the mica plate,equivalent thermal conductivity coefficient of the composite gained through ANSYS simulation more approached the predicted value gained through the formula;when thermal flux flowed along the radial direction of the mica plate,as mica volume fraction rose,the predicted value of equivalent thermal conductivity coefficient of the composite presented exponential growth and is higher than the result of ANSYS.The finite element result and the formula in this paper showed equivalent thermal conductivity coefficient of flake filler polymer composite could be decomposed to contributions at different directions along the thermal flux;longer equivalent thermal conductivity path made flake particles provide more outstanding thermal conduction property after filling the polymer.
polymer composite;flake filler;thermal conductivity;finite element simulation;equivalent thermal resistance
TB332
A
(责任编辑:李启正)
1673-3851(2014)02-0165-06
2013-11-04
朱凤博,(1988-),男,湖北十堰人,硕士研究生,主要研究方向:复合材料及先进复合加工技术。
张顺花,E-mail:zshhzj@163.com
