基于文氏振荡器的忆阻混沌电路
2014-05-22李志军曾以成
李志军曾以成
基于文氏振荡器的忆阻混沌电路
李志军*①曾以成②
①(湘潭大学信息工程学院 湘潭 411105)②(湘潭大学光电工程系 湘潭 411105)
该文采用文氏桥振荡器和磁通控制的分段线性忆阻器,设计了一种新的单一参数控制的混沌电路。通过调节控制参数,该系统在忆阻器的非线性作用下,通过倍周期分岔产生了混沌和超混沌现象。利用常规的动力学分析手段研究了电路参数变化时系统的动力学特性,例如平衡点稳定性分析,李雅普诺夫指数谱和分岔图。为了验证电路的正确性,该文采用集成运放和压控开关实现了一个分段线性磁控忆阻器的模拟等效电路,并将该系统应用于提出的混沌电路,Pspice仿真结果与理论分析完全吻合。
混沌电路;忆阻器;分段线性;文氏桥振荡器
1 引言
2008年5月惠普实验室研究小组采用纳米技术实现了具有“记忆”特性的电阻[1],从而证实了文献[2,3]提出的忆阻器概念和相关理论。作为与电阻,电感,电容并列的第4个基本无源器件,忆阻器建立了磁链和电荷之间的关系,其阻值与两端的电压幅度、极性和工作时间有关。由于忆阻器具有“记忆”功能,其潜在的应用价值引起了国内外学者的广泛关注。利用其数字工作方式,忆阻器可以实现非易失性阻抗存储器(RRAM)和现场可编程门阵列(FPGA)[4];利用其模拟工作方式,忆阻器可以实现人工神经网络和新型类脑系统[5]。

本文采用RC桥式振荡器和PWL型忆阻器设计了一种新的混沌电路。该电路主要利用RC桥式振荡器构成振荡电路,线性电阻和线性电容组成移相网络,通过调节移相电容的大小,电路在忆阻器的非线性作用下从倍周期分岔进入混沌和超混沌状态。采用相图、李雅普诺夫指数谱、分岔图等常规的混沌分析方法研究了电路参数改变时系统的复杂动力学行为。为了从电路方面验证其混沌行为,我们采用常用的电子器件实现了一个PWL型忆阻器的等效实现电路。Pspice软件仿真结果与理论分析及数值仿真完全吻合。
2 电路描述
采用文氏桥振荡器和忆阻器实现的混沌电路如图1所示,其中运放A及外围元件构成文氏桥振荡器,电阻和电容1构成移相网络,忆阻器充当非线性器件使电路中的电压或电流产生突变。在该电路中,忆阻器的类型为分段线性的有源磁控忆阻器,其磁链和电荷之间的关系曲线如图2所示,其数学表达式为[8]

根据忆阻器的赋定关系,可以得到其忆导值为
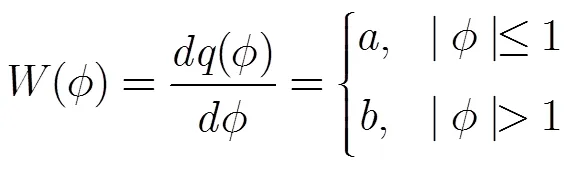
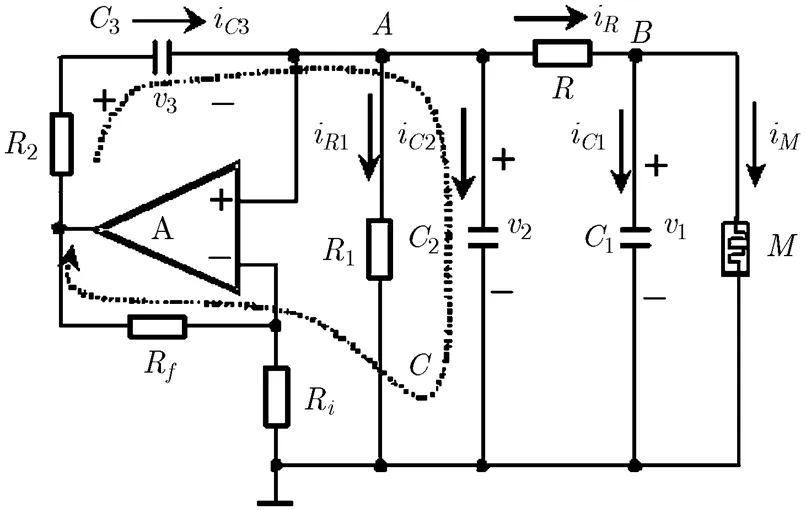
图1 本文提出的忆阻混沌电路

图2 有源磁控忆阻器-q曲线
则忆阻器的端电压和电流之间的关系可以表示为

根据基尔霍夫电流定律可以列出图1电路中节点,的电流方程

由回路可以求出流过电容3的电流为



根据文氏振荡器的要求,1=2,2=3,并设

则式(6)的无量纲状态方程为

其中

很明显,本文提出的混沌电路为一个4维系统,其动力学特性由式(8)决定。
3 系统的基本动力学特性
3.1 对称性和不变性

3.2 衡点及稳定性分析
令式(8)方程右边等于零,可以得到系统的平衡点为={(,,,)|===0,=},即轴上所有的点均可能为平衡点。在平衡点附近将式(8)线性化,得到如式(10)的Jacobi矩阵

其特征值方程为

3.3 系统参数的影响
随着系统参数的变化,系统平衡点的稳定性也会发生变化,系统将处于不同的状态。利用李氏指数谱、分岔图和相图对本文提出的混沌电路进行动力学分析。
4 仿真实验
4.1 忆阻器的等效电路实现


由文献[1~3]可知,忆阻器在一定的频率范围内具有“记忆”特性,当超过一定频率时,忆阻器的“记忆”功能消失并蜕化为线性电阻。对于本文提出的等效电路,我们可以推导出有效工作频率范围。设忆阻器的输入电压为

图3 系统随变化时李氏指数谱和分岔图

图4 典型的z-w相图

则忆阻器两端的磁链对应为(设初始值为0)

由上述工作过程可以看出,当忆阻器两端的磁链始终小于阈值1,即

时,忆阻器蜕化为线性电阻,对应的电导值为-1/R。从而可以推导出该电路的有效工作频率为

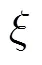
4.2 仿真结果
采用图5的有源忆阻器实现电路替换图1电路中的忆阻器,设置参数=7.5,=0.061,=2.1,=1,=-1.2,=-0.7并取电阻,电容2=3=47 nF,根据式(7)对电路参数进行反归一化得到:1=420 pF,1=2=,R=,R=3。忆阻器等效实现电路的参数设置为R=,R=,4=5=,7=,5=47 nF,8=,10=11=。运算放大器采用AD711AKN, 压控开关采用高速集成开关ADG2012AKN,电源电压为±12 V。应用Pspice软件对电路进行仿真得到的v1-v2和v1-相图分别如图6 (a), 6(c)所示。图6(b), 6(d)为对应的数值仿真结果。比较两组仿真结果可以看出,理论分析、数值仿真与Pspice仿真结果基本一致,从而证明提出的混沌电路及忆阻器等效电路是正确有效的。值得注意的是,由于忆阻器的等效电路中存在积分漂移从而导致图6(a)与6(b),图6(c)与6(d)之间存在一定的失真,在实际应用中可以采用低漂移的集成运放来减小失真。v1和忆阻器两端磁通的瞬时波形如图7所示,表明它们是非周期性的,随机变化的。图8为忆阻器独有的收缩迟滞曲线,即当忆阻器两端电压为零时,流过忆阻器的电流总是为零。
5 结论
本文采用文氏桥振荡器和磁控PWL忆阻器设计了一种新的混沌电路,并通过理论分析、李氏指数谱、分岔图和相图等方法分析了系统的基本动力学行为,验证了系统随参数变化时由倍周期分岔产生混沌和超混沌行为的动力学特性。为了验证系统的正确性,本文采用通用的运算放大器和压控开关设计了一个新的PWL型忆阻器的模拟等效电路,并对提出忆阻器混沌电路进行了Pspice仿真分析。理论分析、数值仿真和Pspice仿真结果基本一致,验证了电路的正确性和有效性。由于所设计的忆阻器混沌电路具有很好的鲁棒性(不含电感),而且可以采用通用的电子器件实现,因而在保密通信、微弱信号检测和电子测量等领域具有潜在的应用价值[19]。

图6 Pspice仿真结果与数值仿真结果比较


图8 忆阻器的收缩迟滞曲线
[1] Strukov D B, Snider G S, Stewart G R,The missing memristor found[J]., 2008, 453(1): 80-83.
[2] Chua L O. Memristors-the missing circuit element[J]., 1971, 18(5): 507-519.
[3] Chua L O and Kang S M. Memristive devices and systems[J]., 1976, 64(2): 209-223.
[4] Shin S, Kim K, and Kang S M. Memristive XOR for resistive multiplier[J]., 2012, 48(2): 78-80.
[5] Shin S, Kim K, and Kang S M. Memristor applications for programmable analog ICs’[J]., 2011, 10(2): 266-274.
[6] 朱从旭, 胡玉平, 孙克辉. 基于超混沌系统和密文交错扩散的图像加密新算法[J]. 电子与信息学报, 2012, 34(7): 1735-1743.
Zhu Cong-xu, Hu Yu-ping, and Sun Ke-hui. New image encryption algorithm based on hyperchaotic system and ciphertext diffusion in crisscross pattern[J].&, 2012, 34(7): 1735-1743.
[7] Juan L, Mata-Machuca, Rafael Martínez-Guerra,A chaotic system in synchronization and secure communications[J]., 2012, 17(4): 1706-1713.
[8] Itoh M and Chua L O. Memristor oscillators[J]., 2008, 18(11): 3183-3206.
[9] Muthuswamy B and Kokate P P. Memristor-based chaotic circuits[J]., 2009, 26(6): 415-426.
[10] Muthuswamy B and Chua L O. Simplest chaotic circuit[J]., 2010, 20(5): 1567-1580.
[11] Bao B C, Liu Z, and Xu J P. Steady periodic memristor oscillator with transient chaotic behaviours[J]., 2010, 46(3): 237-238.
[12] Iu H H C, Yu D S, Fitch A L,Controlling chaos in a memristor based circuit using a Twin-T notch filter[J].
:, 2011, 58(6): 1337-1344.
[13] Bao B C, Liu Z, and Xu J P. Transient chaos in smooth memristor oscillator[J]., 2010, 19(3): 030510-1-030510-6.
[14] Bao B C, Xu J P, Zhou Guo-hua,.. Chaotic memristive circuit: equivalent circuit realization and dynamical analysis[J]., 2011, 20(12): 120502-1-120502-7.
[15] Muthuswamy B. Implementing memristor based chaotic circuits[J]., 2010, 20(5): 1335-1350.
[16] Messias M, Nespoli C, and Botta V A. Hopf bifurcation from lines of equilibria without parameters in memristors oscillators[J]., 2010, 20(2): 437-450.
[17] Shin S and Kang S M. Compact models for memristors based on charge-flux constitutive relationships[J]., 2010, 29(4): 590-598.
[18] Biolek Z, Biolek D, and Biolkova V. Spice model of memristor with nonlinear dopant drift[J]., 2009, 18(2): 210-214.
[19] 郑皓洲, 胡进峰, 徐威, 等. 一类新型超混沌系统的非线性反馈同步研究[J]. 电子与信息学报, 2011, 33(4): 844-848.
Zheng Hao-zhou, Hu Jin-feng, Xu Wei,Study on synchronization of a new class of hyperchaotic systems using nonlinear feedback control[J].&, 2011, 33(4): 844-848.
李志军: 男,1973年生,副教授,硕士生导师,研究方向为非线性系统、电流模式电路和数模混合集成电路.
曾以成: 男,1962年生,教授,博士生导师,感兴趣的研究方向有非线性电路、混沌信号处理、语音信号处理.
A Memristor Chaotic Circuit Based on Wien-bridge Oscillator
Li Zhi-jun①Zeng Yi-cheng②
①(,,411105,)②(,,411105,)
A novel chaotic circuit with a single bifurcation parameter is presented in this paper. The circuit is composed of a Wien-Bridge oscillator and a piecewise-linear memristor. By adjusting the system parameter, the proposed circuit performs chaotic and hyper-chaotic behaviors from doubling-periodic. The dynamic properties of the new circuit are demonstrated via universal dynamics analysis methods such as equilibria stability, Lyapunov exponent spectra and bifurcation diagrams. An equivalent circuit which realizes the action of three segments piecewise linear flux- controlled memristor is proposed and employed to the chaotic circuit. The Pspice simulation results of the resultant circuit are consistent with theoretical analysis.
Chaotic circuit; Memristor; PieceWise-Linear (PWL); Wien-bridge oscillator
TN918
A
1009-5896(2014)01-0088-06
10.3724/SP.J.1146.2013.00332
2013-03-15收到,2013-09-10改回
国家自然科学基金(61176032)资助课题
李志军 lizhijun_320@163.com
