随机移动模型下移动自组网无序传输端到端延迟闭解分析
2014-05-22王晓菲
王晓菲 蔡 英② 李 卓②
随机移动模型下移动自组网无序传输端到端延迟闭解分析
王晓菲①蔡 英*①②李 卓①②
①(北京信息科技大学计算机学院 北京 100101)②(北京信息科技大学网络文化与数字传播研究北京市重点实验室 北京 100101)
针对移动自组网端到端延迟在封闭形式分析方面的局限性,该文提出一种有效的针对无序传输,单副本两跳中继算法的网络延迟建模方案,并给出其严格的理论延迟上界。首先针对多种随机移动模型,证明了移动节点的相遇间隔时间可归纳为统一表达式。然后,综合分析了媒介竞争、流量竞争、排队延迟等问题,合理划分并精确求解出了各延迟关键时间段,从而构造了数据包排队服务模型。最后推导出移动自组网端到端延迟的封闭形式理论上界。仿真结果表明,该理论延迟与实验数据紧密吻合。
移动自组网;端到端延迟;随机移动模型;无序传输;排队服务模型
1 引言
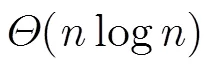
显然,上述渐近式分析方案只能从宏观上描述延迟时间的变化趋势,而确切的延迟描述方法更能引发网络设计者的强烈兴趣,通常可借助封闭式求解方法加以解决,现有研究主要局限于采用i.i.d.移动模型的有序传输方式,例如:文献[11]中分别讨论i.i.d.移动模型下两跳及多跳中继算法,同时给出端到端延迟的封闭形式精确解表达式。文献[14]为方便灵活操控延迟,设计副本两跳中继算法以支持冗余包传输,指出基于i.i.d.模型的端到端延迟的封闭形式上限是源端与目的端平均服务时间的函数。此外,2012年提出的一种基于组传输的两跳中继方案[15]解决了无序接收方式下封闭式平均传输延迟的分析问题。然而,该方案忽略了发送端数据包的排队等待时间。
若将移动模型划分为随机移动模型与受限移动模型两类[17],文献[18]已经证明其中的随机移动模型与i.i.d.移动模型在某些条件下存在等价性,这为精确衡量节点相遇行为提供了理论依据。基于此,针对无序传输方式,本文试图在两跳,单副本且存在干扰或竞争的中继条件下,提出一种可广泛适用于多种随机移动模型的端到端延迟封闭形式分析方案,以克服上述弊端,并经仿真实验证实有效。
2 系统模型与中继算法
2.1 网络模型
将单位平方网络范围划分为×个小区,初始时刻随机分布有个移动节点。选用一种基于时隙且快速移动[14]的网络场景,忽略移动模型复杂的边界效应,并规定每个节点在任一时隙持续期间仅归属于唯一的一个小区,每个时隙能够成功传输的最大比特数固定为一个数据包。每个时隙至多允许节点在相遇条件下一同完成一次发送和一次接收,以及为某一数据分组提供的一次副本转发。
为简便起见,下文分别用标记,和依次代表源节点、目的节点和中继节点。
2.2 流量模型
2.3 调度模型
局部传输场景要求任意时隙位于某一小区中的节点只能向位于相同小区中的邻居节点传送数据包,即网络通信范围近似取值为(21/2)/。同时可引入传输组概念[14]有效避免无线传输资源竞争与干扰。任意两个水平距离且垂直距离均为整数倍的小区属于相同传输组。为确保位于相同传输组内的节点可以同时传输而不会发生相互干扰,的取值十分关键[14],需满足式(1):

2.4 单副本两跳中继算法
单副本两跳中继算法规定包副本数上限为1,且源节点发出的每个数据包在到达目的节点之前最多经历两跳传输。中继节点或目的节点在收到一个完整的数据包后,立即对其进行处理,并从接收缓存队列中删除该包。两跳中继网络每时每刻只存在3类传输形式,即-传输,-传输和-传输。当传输条件同时成立时,由于直接传输方式的开销相对较低,故一般具有最高的优先级。
3 相遇间隔时间
3.1 任意节点相遇间隔时间
源节点与任意节点相遇是数据包在端完成发送过程的前提。本节推导任意节点每次相遇所需等待的间隔时间,进而度量发送服务效率。因i.i.d.模型下节点位置在任意时隙呈现均匀分布,可知任意两节点自初态起在第步相遇的概率为1/2,故某节点与其余任意节点(至少一个)在第步相遇的概率为
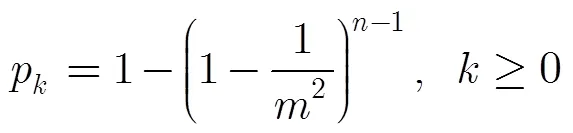
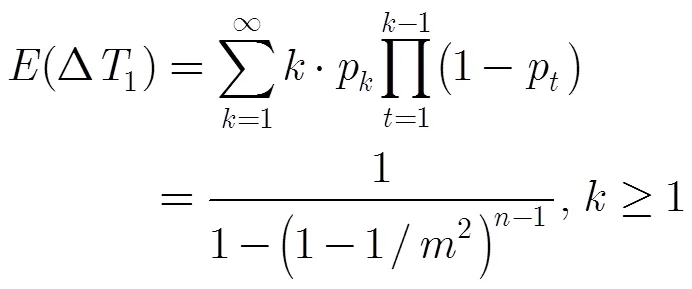
3.2 选定节点相遇间隔时间
两跳中继算法指出数据包副本自源节点发送至某一中继节点后,需经完成向某一固定目的节点的转发操作。本节为此推导与每次相遇所需等待的平均间隔时间,用以描述端转发服务效率。依据i.i.d.模型定义,任意节点在任意时隙位于任意小区的概率均为1/2,可知若将两选定节点,首次相遇的时隙视作时刻0,则其后二者在第步相遇的概率为


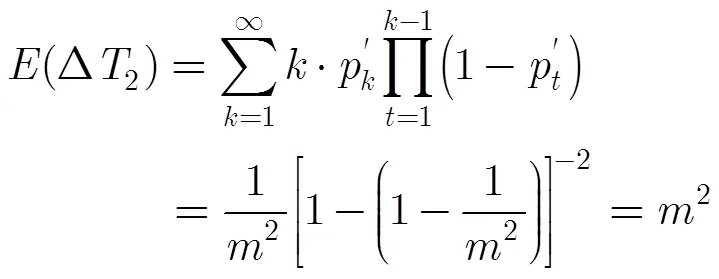
3.3 随机移动模型的等价性
按照节点的移动特性,可以将移动模型划分为随机移动模型与受限移动模型两大类[17]。前者主要包括随机漫步移动模型[13]、随机路径点移动模型[13]等。Cai 等人[18]的研究工作充分讨论了随机移动模型与i.i.d.模型满足某些约束条件时存在的等价关系,因而本文采用i.i.d.模型对节点相遇时间进行整体讨论。
引理1 在严格基于时隙且快速移动的网络模型下,若各节点初始位置均匀分布,各时隙移动方式一致且独立,则采用随机移动模型的节点在任意时隙位于某一小区的概率为1/2,节点位置呈现均匀分布。
引理2 在严格基于时隙且快速移动的网络模型下,若各节点初始位置集中于一个小区,各时隙移动方式一致且独立,则采用随机移动模型的节点在任意时隙位于某一小区的概率随着移动次数的增加快速趋向1/2,节点位置近似于均匀分布。
由引理1可知,节点在任意时隙下所处位置的概率等同于i.i.d.模型,节点初始时刻的均匀分布状态未随时间而发生任何改变,任意两节点在相同小区相遇的概率仍为1/2,故式(2)与式(3)显然成立;由引理2可知两选定节点在某一小区发生相遇,二者此后的相遇概率虽在短期内受到上次相遇位置的影响,但二者再次相遇时各节点所处位置已无限接近于均匀分布,此时相遇概率可近似取值为1/2,即式(4)与式(5)成立。综上,本文针对i.i.d.模型围绕任意节点两类相遇间隔时间的推导方法及结论,同样适用于多种常见的随机移动模型。
4 排队服务模型
本节在随机移动模型节点相遇时间间隔的研究基础上,分别为源节点和中继节点构造两类排队模型,并借助概率描述各类传输事件及通信链路的发生条件,可作为后续延迟推导的基础。
4.1 延迟基本定义及划分
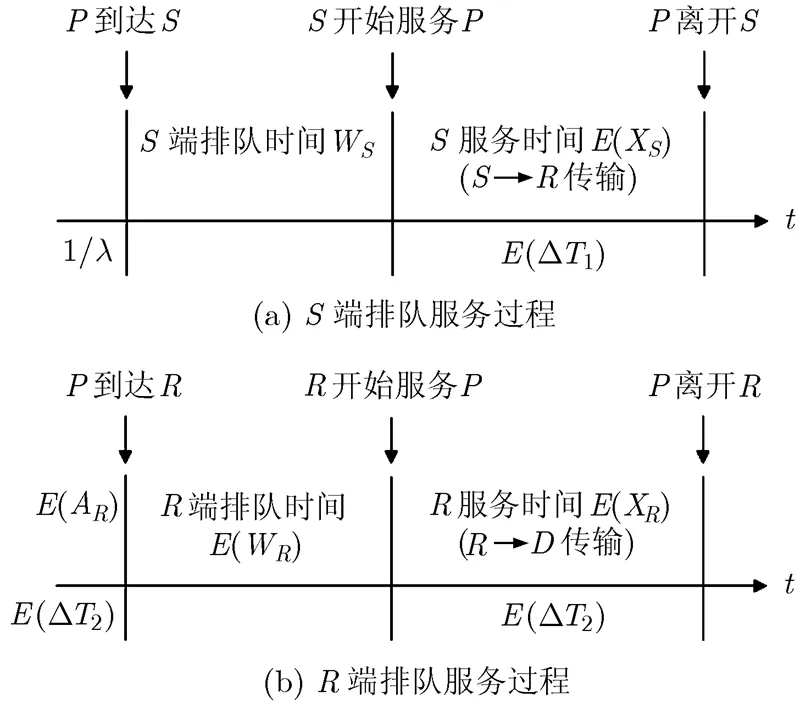
图1 端到端延迟阶段划分
4.2 S端排队模型

定理2服务时间X的期望与方差上界为

证明 由定理1结论可知,节点与节点在相遇后以概率1发生传输,故而
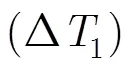
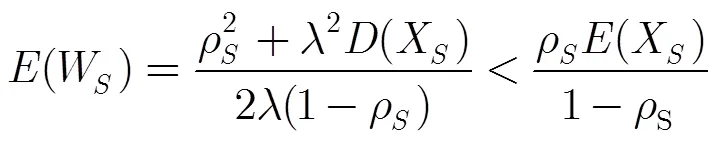
4.3 R端排队模型

定理3 两节点在相遇条件下发生-传输的概率为

化简上式可得式(9) 证毕。
定理4端包副本到达时间间隔A的期望与方差上界为

证明 详细过程请参照定理2证明。
定理5 两节点在相遇条件下发生-传输的概率为
证明 详细过程请参照定理3证明。 定理6服务时间X的期望与方差上界为


随着文化程度的提高,医务人员院感知识认知正确率逐渐增高,这个结果与邱湖海等[15]在2015年的研究报道是一致的。不过不同文化程度的医务人员对医院污物处理认知程度上并没有显著差异,平均认知正确率仅有66.36%,说明即便文化程度较高的医务工作者对于医院污物处理的认知也是不足的,提示在以后的医院感染培训中要着重加强医院污物处理方面的培训内容。

5 端到端延迟闭解方案
本节利用第4节中所得端排队模型与端排队模型的相关结论,推导出端到端延迟上界的封闭表达式。首先,为精确度量包的端到端延迟,并最大限度合理约束理论上界,考虑不同通信链路的影响因素,特别是直接传输方式下对端服务额外耗时的合理解决方案。
对于––传输,如图1(b)所示,包延迟上界为W+(X)+(W)+(X)。
定理7-成功传输概率为
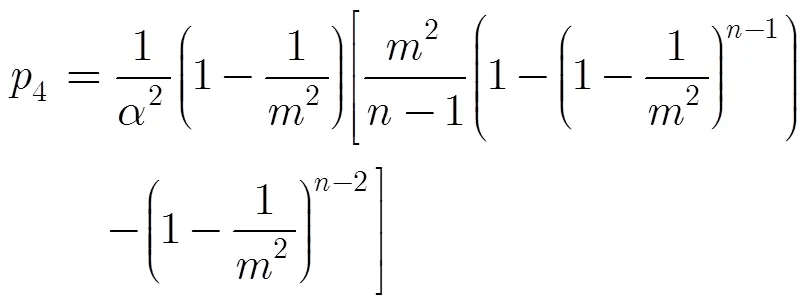

证毕
定理8-成功传输概率为
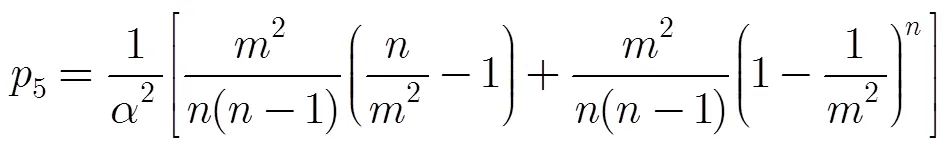

因此,包最终经––过程或-过程得以传输的概率分别为


仿照相似的推导思路,可将本文闭解方案推广至多跳中继环境。具体证明过程从略。
6 仿真结果与分析
仿真器依据系统模型的相关要求,在C++环境中设计并实现封闭形式端到端延迟上界的理论值计算以及单副本两跳中继的无序接收传输调度过程。仿真程序包含随机数生成模块,输入流控制模块,传输机会竞争模块,传输组管理模块,总传输调度模块以及i.i.d.移动模型[11],随机漫步移动模型[9]等。通过对比实验数据与理论延迟上界,分析验证i.i.d.移动模型及多种常见随机移动模型下移动自组网端到端延迟性能。
6.1 网络参数设置
模拟程序以当前系统时间作为随机种子,以i.i.d.移动模型,随机漫步移动模型和随机路径点移动模型为例。仿真实验运行总数达到107时隙,网络主要参数依次设定为=8,=64,取值区间为(0,1),并约定保护因子=1,则式(1)可相应地化简为=min{4,}=4。
6.2 理论结果准确性验证

表1端到端延迟各阶段理论值与实验值对照

理论值实验值理论值实验值 i.i.d.WalkWayPointi.i.d.WalkWayPoint 0.300.50 E()1.591.59 1.59 1.59 1.59 1.59 1.59 1.59 E()64.0064.12 64.39 64.19 64.00 64.10 64.13 63.88 E(XS)60.5559.68 60.33 59.53 60.55 60.07 60.47 59.45 E(XR)..3838.403849.183818.283811.323838.403834.433836.343830.99 0.700.90 E() 1.59 1.59 1.59 1.59 1.59 1.59 1.59 1.59 E()64.00 63.97 64.07 64.22 64.00 64.02 63.97 63.76 E(XS)60.55 60.43 60.75 59.93 60.55 60.38 60.36 60.33 E(XR)3838.403842.503838.163846.843838.403846.033835.663843.54
此外,不同移动模型下端到端延迟的理论上界与实验数据对比如图2。在忽略程序随机性误差的前提下,表1证实了各延迟阶段的理论分析结论,实验结果与之紧密吻合。图2验证了端到端延迟理论上界在不同移动模型下的有效性。该图线表明实验数据与理论上界紧密匹配,且随着输入负载逐渐向1逼近,延迟的平均增长速率持续提升。
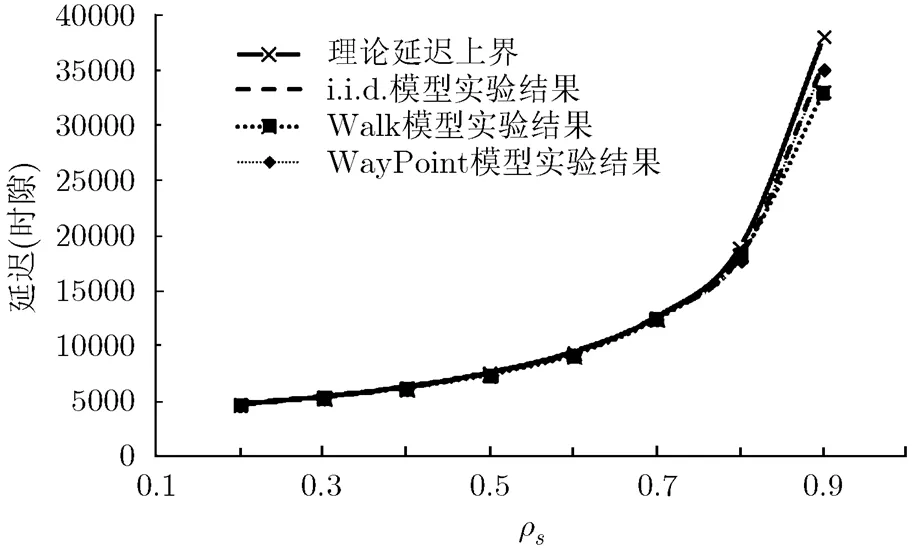
图2 网络端到端延迟理论上界与模拟仿真结果对比
7 结束语
封闭形式网络延迟推导是移动自组网性能分析的关键问题之一,而在不同随机移动模型下围绕端到端延迟的研究目前尚不充分。本文将多种常见随机移动模型合理化转为i.i.d.移动模型,针对无序传输环境选用单副本两跳中继算法,重点讨论存在干扰、竞争的数据包排队服务过程,从而计算出移动自组网端到端延迟的封闭形式紧密上界,最终编程模拟验证了理论结果。
[1] Fujishiro N, Nakano H, and Miyauchi A. A routing algorithm for mobile Ad hoc networks based on multi-agent cost learning[J]., 2013, 7(1): 67-72.
[2] Liu Y Y. Stable routing algorithm for mobile Ad hoc network[J]., 2011, 6(8): 1171-1178.
[3] Liang D. Opportunistic media access control and routing for delay-tolerant mobile Ad hoc networks[J]., 2012, 18(8): 949-965.
[4] Ikeda M, Kulla E, Barolli L,.. Performance evaluation of wireless mobile ad-hoc network via NS-3 simulator[C]. Proceedings of 14th International Conference on Network-Based Information Systems (NBiS 2011), Tirana, 2011: 135-141.
[5] Vaidya B, Denko M K, and Rodrigues J J P C. Security mechanism for voice over multipath mobile Ad hoc networks[J]., 2011, 11(2): 196-210.
[6] Otero A S and Atiquzzaman M. Ad aptive localized active route maintenance mechanism to improve performance of VoIP over ad hoc networks[J].s, 2011, 6(1): 68-78.
[7] Greco C, Cagnazzo M, and Pesquet-Popescu B. Low-latency video streaming with congestion control in mobile Ad-hoc networks[J]., 2012, 14(4): 1337-1350.
[8] Zhou L, Zhang Y, Rodrigues J,.. Quality-delay tradeoff for video streaming over mobile Ad hoc networks[C]. Proceedings of 2012 IEEE International Conference on Communications (ICC 2012), Ottawa, 2012: 223-227.

[10] Sharma G, Mazumdar R, and Shroff N B. Delay and capacity trade-offs in mobile Ad hoc networks: a global perspective[J]./, 2007, 15(5): 981-992.
[11] Neely M J and Modiano E. Capacity and delay tradeoffs for Ad-hoc mobile networks[J]., 2005, 51(6): 1917-1937.
[12] Sharma G and Mazumdar R. Delay and capacity trade-off in wireless Ad hoc networks with random mobility[OL]. http://ece.uwaterloo.ca/mazum/M2004.pdf, 2013, 11.
[13] Zhou S and Ying L. On delay constrained multicast capacity of large-scale mobile Ad-hoc networks[C]. Proceedings of 29th IEEE International Conference on Computer Communications (INFOCOM 2010), San Diego, 2010: 131-135.
[14] Liu J J, Jiang X H, Nishiyama H,.. Delay and capacity in Ad hoc mobile networks with f-cast relay algorithms[J]., 2011, 10(8): 2738-2751.
[15] Liu J J, Jiang X H, Nishiyama H,.. Generalized two-hop relay for flexible delay control in MANETs[J]., 2012, 20(6): 1950-1963.
[16] Cai Y, Wang X F, Li Z,. Delay and capacity in MANETs under random walk mobility model[OL]http://link.springer.com/article/10.1007% 2Fs11276-013- 0617-6#. 2013.
[17] 童超, 牛建伟, 龙翔, 等. 移动模型研究综述[J]. 计算机科学, 2009, 36(10): 5-9.
Tong Chao, Niu Jian-wei, Long Xiang,.. Survey on mobility model[J]., 2009, 36(10): 5-9.
[18] Cai Y, Wang X F, and Zhang Y Q. The analysis of mobility models in MANETs with two-hop relay algorithm[C]. Proceedings of 4th International Conference on Intelligent Networking and Collaborative Systems (INCoS 2012), Bucharest, 2012: 229-236.
[19] Li P, Fang Y, and Li J. Throughput, delay, and mobility in wireless Ad-hoc networks[C]. Proceedings of 29th IEEE International Conference on Computer Communications (INFOCOM 2010), San Diego, 2010: 1-9.
[20] 盛友招. 排队论及其在现代通信中的应用[M]. 北京: 人民邮电出版社, 2007: 68-71.
王晓菲: 女,1990年生,硕士生,研究方向为无线网络、信息安全.
蔡 英: 女,1966年生,博士,教授,研究方向为无线网络、信息安全.
李 卓: 男,1983年生,博士,讲师,研究方向为无线网络、移动计算.
Closed-form Solution of End-to-end Delay with Out-of-order Delivery in MANETs under Random Mobility Models
Wang Xiao-fei①Cai Ying①②Li Zhuo①②
①(&,100101,)②(,&,100101,)
Due to the limitation of the closed-form analysis of end-to-end delay in mobile ad hoc networks, this paper develops an effective modeling scheme for delay in the networks where the delivery is out-of-order and the two-hop relay algorithm with single copy is involved, and presents a rigorous theoretical upper bound. First, for various random mobility models, it is proved that the inter-meeting time between mobile nodes can be expressed in a unified expression. Furthermore, taking the medium competition, the traffic competition and the queuing delay into consideration, the critical time period of delay is defined accurately, and then the queuing service is modeled. Finally, an exact upper bound of the end-to-end delay is derived in closed-form. Simulation results validate that the theoretical delay matches the experimental data closely.
Mobile Ad hoc NETworks (MANETs); End-to-end delay; Random mobility model; Out-of-order delivery; Queuing service model
TP393
A
1009-5896(2014)01-0034-07
10.3724/SP.J.1146.2013.00155
2013-01-29收到,2013-10-22改回
北京市教委科技发展计划面上项目(KM201311232014, KM201411232013)资助课题
蔡英 ycai@bistu.edu.cn
