凹包内散乱点集Delaunay四面体角度剖分算法

李世森，王熹芳

（天津大学，天津 300072）

凹包内散乱点集Delaunay四面体角度剖分算法

李世森，王熹芳

（天津大学，天津 300072）

在邵铁政［1］三维空间散乱点集Delaunay四面体剖分算法的基础上，提出了一种不含有除法运算（不存在被0除或丧失计算精度的情形）的通用的判定空间两三角形内交的算法，可以实现凹包内散乱点集的Delaunay四面体剖分。该算法已经通过Fortran语言编程实现并且给出了算例。

散乱点；Delaunay规则；空间三角形内交；四面体

Biography：LI Shi⁃sen（1969-）,male,associate professor.

Delaunay三角剖分算法起源于1934年俄国数学家Delaunay提出的Delaunay准则［2］。在应用有限元方法解决各类问题时，Delaunay网格有严谨的数学证明，能够生成形态优化的网格［3］，是网格划分的主要方法之一。目前，Delaunay三角剖分算法广泛地应用于计算机图形学、航天、地质、土木工程等领域，体现了较强的实用价值。

Delaunay三角剖分算法大致可以分为三类：分而治之算法、逐点插入算法和三角网增长法［4］。虽然二维的Delaunay三角剖分算法已经取得了一定的成果，但是三维空间的Delaunay四面体剖分算法，由于三维空间外包面的复杂性，目前的研究还不够成熟。如文献［5-6］需要先从任意多面体中剖分出一个凸空间，得到一个新的多面体，再把剖分出来的凸空间分割成多个四面体，再重复对新的多面体进行剖分，直至剖分完毕；文献［7-9］在对空间散乱点集进行Delaunay四面体剖分时，需要先将散乱点集的外边界进行Delaunay三角剖分，由边界面生成初始四面体，再通过交换或寻找几何关系将初始四面体剖分更新为新的四面体。

本文提出了对边界面已知的，外包面为凹的空间散乱点进行Delaunay四面体剖分的算法。通过引入对于空间2个三角形是否内交的判断，保证了生成的四面体在凹包边界面的里侧，实现了凹包内散乱点集的Delaunay四面体剖分。

1 凹包内散乱点Delaunay四面体网格生成方法

1.1 相关概念

为了有效地解决凹包内散乱点Delaunay四面体剖分，本算法给出了空间两三角形内交的定义。

空间两三角形内交定义为在三维空间内，当一个三角形三条边所围成的区域与另一个三角形三条边所围成的区域的交集为一条线段时，则称作两三角形内交。在本算法中，当该线段与三角形的某一条边重合时，不认为两三角形内交。

1.2 基本思路

［1］在Delaunay准则定义［3］、球缺角定义［1］、四面体球缺角定义及特性［1］的基础上，给出了凸包内散乱点集Delaunay四面体剖分算法，本算法在此基础上又加入了判断空间两三角形内交的算法。给定一个空间散乱点集以及该散乱点集的外包面（以空间三角形面组成），首先用参考文献［1］中的方法对散乱点集进行Delaunay四面体划分，然后判断生成四面体的各个面是否与已知的边界面内交。若内交继续寻找下一点构成四面体，若不内交，则生成一个Delaunay四面体，这样就使得参考文献［1］中的方法能够处理凹包面内的散乱点。

1.3 判断空间两个三角形内交的数学方法

为了判断这两三角形是否内交，需要首先分别判断一个三角形的三条边所在的直线与另一三角形所在平面的位置关系：相交、平行（交点在无穷远处相交）、在面内（有无穷多个交点）。以判断三角形Q1Q2Q3的边Q1Q2所在直线与平面K1的位置关系为例，有联立方程组

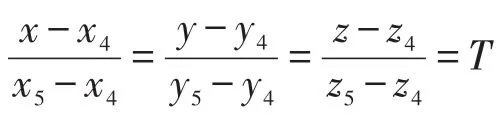
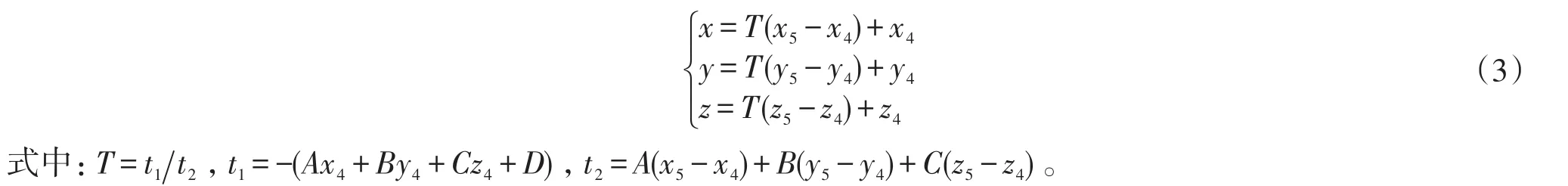
如果直接采用式（3）这一表达式进行计算机编程，当t2=0时（或者t2非常的接近于0时），会造成计算机数值溢出（或者计算结果丧失精度）。即式（3）在计算机中并不是总能求出具体的数值（但是式（3）在任何情况下，在数学上都可以做为交点坐标的表达式），因此式（3）在后续的算法中一直保持表达式的形式。

求解完直线Q1Q2与平面K1的交点表达式后，需要进一步判断交点与线段Q1Q2的位置关系。设直线Q1Q2与平面K1的交点为Q4（x7,y7,z7），将x7,y7,z7的表达式依次带入 （x4-x7）×（x7-x5），（y4-y7）×（y7-y5），（z4-z7）×（z7-z5）中，则可以得到

通过判断式（4）、（5）、（6）的正负来确定交点Q4与线段Q1Q2的位置关系。又因为和（x5-x4）2不影响式（4）、（5）、（6）的正负，所以只需要判断-t1（t1-t2）（令M=-t1（t1-t2））的正负即可。当M值为正时，则Q4内分线段Q1Q2（可以说平面K1内分线段Q1Q2）；当M值为负时，则Q4外分线段Q1Q2（可以说平面K1外分线段Q1Q2）；当M值等于0时，则线段Q1Q2至少有一个端点在平面K1上。

至此，不需要求出式（3）具体数值，而采用无除法表达式M的正负，即可判断线段与平面的位置关系。

当三角形Q1Q2Q3的某一条边被平面K1内分时，则三角形Q1Q2Q3与平面K1的交集为一条线段（设为Q4Q5）。当三角形Q1Q2Q3的三条边对应的-t1（t1-t2）值均为0时（则必有一条边对应的t2值为0），则可判断为t2值为0的线段在平面K1内，即三角形Q1Q2Q3与平面K1的交集为线段Q4Q5（即Q1Q2），如图1所示。除了上述两种情况之外，空间两三角形不可能发生内交。

同理可得，三角形P1P2P3与平面K2的交集（设为线段P4P5）。两条线段的位置关系（两条线段必然在同一直线上）可能存在如图2所示的5种情况。判断两条交线段位置关系的方法，与上文判断交点与线段位置关系的方法类似（即通过判断交点Q4，Q5与线段P4P5的位置关系和交点P4，P5与线段Q4Q5的位置关系来判定两条交线段的位置关系）。

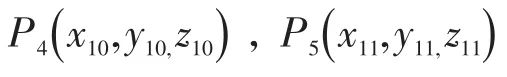
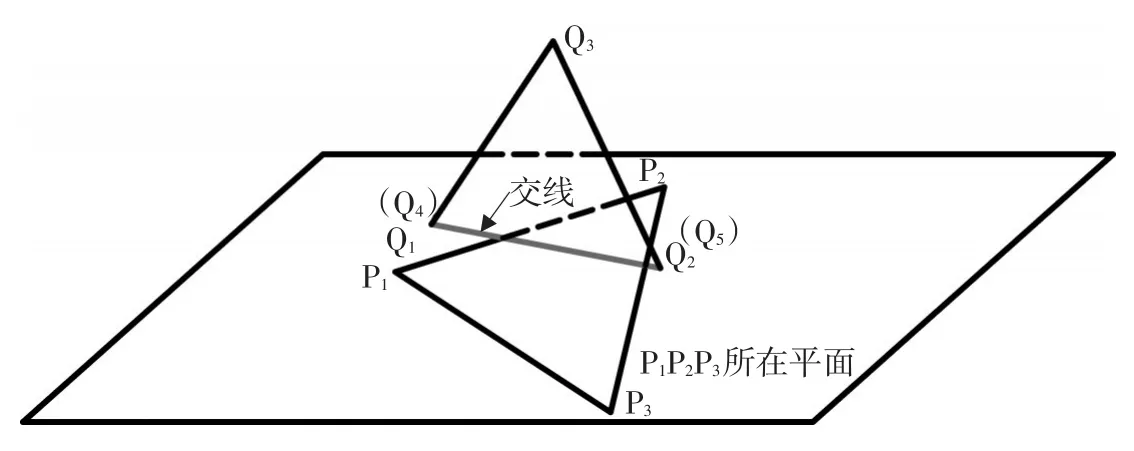
图1 线段Q1Q2在平面内Fig.1 Line segmentQ1Q2on the plane

2 凹包内散乱点四面体剖分的算法

2.1 判断空间两个三角形内交的算法

（1）输入两个三角形的6个点的点号及坐标（xi,yi,zi），（i=1,2…6）。

（2）判断两个三角形是否有公共边（或者完全相同）。若存在公共边，则直接返回空间两三角形不内交；否则，进行步骤（3）。

（3）计算A，B，C，D，E，F，G，H的值。

（4）依次计算各个线段对应的t1和t2的值。

（5）分别判断各个线段对应的-t1（t1-t2）的正负。当-t1（t1-t2）值为正时，标记值为1（存储在数组中）；当-t1（t1-t2）值为负时，标记值为-1；当-t1（t1-t2）等于0时，标记值为0。

（6）检验三角形Q1Q2Q3三条边的标记值。当三角形Q1Q2Q3的三条边，有任意一条边标记值为1时，则进行步骤（8）；当三条边的三个标记值均为0时，则进行步骤（7）。其他情况，直接返回空间两三角形不内交。

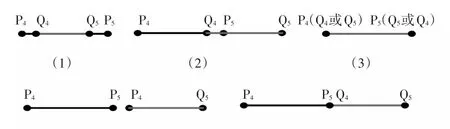
图2 两交线段的位置关系图Fig.2 Positional figure of two intersecting line segments

（7）检验三条边对应t2的值。找出三条边中t2值为0（或者t2非常的接近于0）的边（该边即为线段Q4Q5）。

（8）检验另一三角形P1P2P3的三条边的标记值。方法同步骤（5），（6），（7）。

（9）检验线段P4P5与Q4Q5的位置关系。当R值为正时，标记值为1；当R值为负时，标记值为-1；当R值等于0时，标记值为0（标记值存储在另一数组中）。

（10）判定空间两三角形是否内交。当4个交点（Q4，Q5，P4，P5）标记值有两个为1或者4个交点的标记值均为0时，返回空间两三角形内交；否则返回空间两三角形不内交。

2.2 算法运行框图及算法的输入

本算法所需的输入文件为边界面输入文件和散乱点输入文件。边界面的剖分格式为三角形，边界面数据文件中每一行保存一个边界三角形的三个点的点号，该数据文件的行数即为边界面三角形的个数。散乱点数据文件中每一行保存一个散乱点的坐标，顺序为“x坐标，y坐标，z坐标”，1号点保存在第一行，2号点保存在第二行，以此类推，行数即为空间散乱点的个数。

算法运行框图如图3所示。

2.3 算法的具体步骤

算法具体分为以下几个步骤：

（1）读取边界面三角形及空间散乱点。

（2）用一个变量q记录已生成的四面体个数，用另一个变量p记录已扩展的四面体个数。p和q的初始值为0。

（3）对每一个边界面如下运算：

a）判断该边界面是否出现在已生成的q个四面体中。若未出现，则转到步骤（b）；否则，处理下一个边界面。

b）采用文献［1］的算法，在散乱点中找到一个点与边界面三角形生成一个四面体。

c）检验（b）中生成的四面体的每一个面与所有已知边界面及已生成的四面体的各个面均不内交时，将四面体4个点的点号按顺序保存在数据文件中，q值增加1；否则，从全部点集中临时删除此点，回到步骤（b）。

（4）p值增加1。

（5）比较p，q值。若p＞q，结束；否则，转向步骤（6）。

（6）对第p个四面体的4个三角形进行是否可扩展的判断：若该三角形是边界面，或者是两个四面体的公共面，则不可扩展；否则进行步骤（7）。

（7）对第p个四面体的每一个可扩展的三角形采用文献［1］的算法生成四面体，并且保证该四面体的各个面不与已生成的四面体的各个面内交。将每一个生成的四面体4个点的点号按顺序保存在数据文件中，q值增加1。

（8）转向步骤（4）。

图3 程序运行框图Fig.3 Program operation diagram

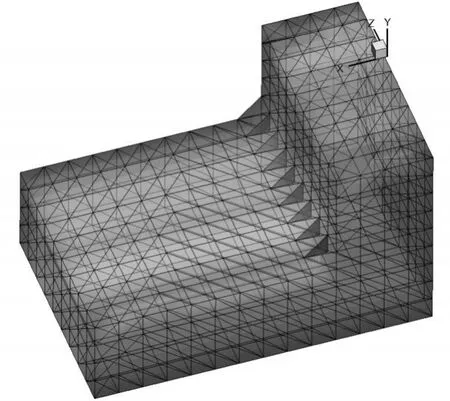
图4 1 000个空间散乱点的效果图Fig.4 Sketch of 1 000 spatial scattered

3 凹包面效果图

本文运用上述算法，对空间散乱点个数为413的空间体进行了Delaunay四面体剖分，得到如图4所示的整体效果图及x，y，z方向的截面图，由于整体效果图中不能很好的显示内部的网格，故而又给出了x，y，z方向的截面图。此外，本文还给出了空间散乱点个数为1 000的L型空间体效果图，如图4所示。可以看到，本算法可以对凹包面内散乱点进行Delaunay四面体剖分，这对空间散乱点集Delaunay四面体剖分算法的研究有一定的意义。

4 结论

（1）本文所述算法沿用了参考文献［1］的算法，即根据四面体球缺角的特性在散乱点中寻找与之构成Delaunay四面体的点的算法。

（2）在参考文献［1］的算法的基础上，本算法又提出了判断空间两三角形内交的算法。

a）当检验空间两三角形是否内交时，若两个需要检验的三角形有公共边（或重复），则不需要进行内交检验。

b）在判断空间两三角形是否内交的一般数学表达式中必然会出现除法运算，而空间两三角形的位置可以千变万化，也就无法保证表达式中的分母不为0。为了得到通用的算法，本文推导出了最终的数学表达式，得到了不含有分母的通用判别式（M，R），可准确判断出任意两个空间三角形是否相交。当最终的数学表达式中对应的分母为0时也对应了一种空间两三角形的位置关系。

c）通过对空间两三角形内交的算法的引入，本算法能够对凹包内散乱点集进行Delaunay四面体剖分。

（3）给出了整个算法实现的具体步骤。

（4）应用本算法对空间散乱点个数为413的空间体进行了Delaunay四面体剖分，并得到了效果图。

参考文献：

［1］邵铁政,李世森.凸包内空间散乱点集Delaunay四面体角度剖分算法［J］.水道港口,2013,146（1）：95-98.

SHAO T Z，LI S S.Delaunay Angle Algorithm of Spatial Scattered Point Set Delaunay Triangulation for Convex Hull［J］.Journal of Waterway and Harbor,2013,146（1）：95-98.

［2］Lawson C L.Software for C1 Surface Interpolation,Mathematical Software III［M］.New York：Academic Press,1977：161-194.

［3］王建华,徐强寻,张锐.任意形状三维物体的Delaunay网格生成算法［J］.岩石力学与工程学报,2003,22（5）：717-720.

WANG J H,XU Q X,ZHANG R.Delaunay algorithm and related procedure to generate the tetrahedron mesh for an object with ar⁃bitrary boundary［J］.Chinese Journal of Rock Mechanics and Engineering，2003,22（5）：717-720.

［4］李丽.三维空间Delaunay三角剖分算法的研究及应用［D］.大连：大连海事大学,2010.

［5］陈一民,李超,熊玉梅.任意多面体的四面体剖分算法［J］.计算机工程与应用,2003（30）：69-93.

CHEN Y M,LI C,XIONG Y M.Algorithm of Dividing an Arbitrary Polyhedron to Tetrahedrons［J］.Computer Engineering and Applications,2003（30）：69-93.

［6］李昌领,张虹,朱海峰.一种任意多面体的四面体剖分的改进算法［J］.计算机工程与应用,2012（25）：20-38.

LI C L,ZHANG H,ZHU H F.Improved Algorithm of Dividing an Arbitrary Polyhedron into Tetrahedrons［J］.Computer Engineer⁃ing and Applications,2012（25）：20-38.

［7］关文革,武强,贾丽萍,等.约束数据域Delaunay四面体网格生成算法［J］.华中科技大学学报：自然科学版,2005（5）：67-69.

GUAN W G，WU Q，JIA L P，et al.Algorithm of mesh generation of Delaunay tetrahedral in constrained domain［J］.Journal of Huazhong University of Science and Technology,2005（5）：67-69.

［8］XU H,WU Q.Design&implementation of visualization for 3d sandwich geological bodies［J］.Computer Applications,2001,21（12）：56-60.

［9］WU Q,XU H.An approach to computer modeling and visualization of geological faults in 3d［J］.Computers and Geoscience,2003,29（4）：503-509.

［10］彭国伦.Fortran95程序设计［M］.北京：中国电力出版社，2010.

Delaunay angle algorithm of scattered point set delaunay triangulation for concave hull

LI Shi⁃sen,WANG Xi⁃fang
（Tianjin University，Tianjin300072，China）

Based onDelaunay Angle Algorithm of Spatial Scattered Point Set Delaunay Triangulation for Con⁃vex Hulldefined by SHAO Tie⁃zheng,a new common algorithm of judging two triangles intersection which did not contain the division（without the case of divided by zero or loss of accuracy）was proposed in this paper,and the algo⁃rithm could solve spatial scattered point set Delaunay triangulation for concave hull.The actual programming opera⁃tion of the new algorithm was also carried out by Fortran,and an example was given.

scattered points;Delaunay rules;spatial triangles intersection;tetrahedron

O 182.2

A

1005-8443（2014）02-0180-05

2013-04-02；

2013-06-20

李世森（1969-），男，河北冀县人，副教授，主要从事港口航道与近海水流、泥沙研究。