单增李斯特菌在牛奶中生长曲线的拟合和预测模型的建立

邹 宇，胡立明，胡文忠，* ，何煜波，刘程惠

(1.大连民族学院生命科学学院，辽宁大连116600;2.空军勤务学院航空军需系，江苏徐州221006)

单增李斯特菌(Listeria monocytogenes)广泛分布于自然界中，存在于肉类、乳制品、蛋类、海产品和蔬菜等大多数食品中［1－2］。单增李斯特菌是人畜共患病的病原菌，也是一种腐生菌，在某些食物(主要是肉类和乳制品)中易于生长繁殖，能引起严重的食物中毒，主要表现为败血症、脑膜炎等［3－4］。该菌在 4℃的环境中仍可生长繁殖，是冷藏食品威胁人类健康的主要病原菌之一［5］。牛奶营养丰富且配比合理，易受到单增李斯特菌的污染［6］，因此，研究单增李斯特菌在牛奶中的生长情况对保障食品安全性是十分必要的。

食品预测微生物学是一门在微生物学、数学和统计学基础上建立起来的新学科［7－8］，通过建立数学预测模型，可定量分析不同环境条件(如温度、湿度、含氧量等)下食品中病原菌和腐败菌的数量，从而对食品中微生物的生长情况作出合理预测。

本实验通过测定5、15、25和35℃条件下单增李斯特菌在牛奶中的细菌总数并拟合生长动力学曲线，进而建立牛奶中单增李斯特菌生长的初级模型和二级模型，为牛奶等食品在贮藏过程中对单增李斯特菌的预测和控制提供理论依据。

1 材料与方法

1.1 材料与仪器

单增李斯特菌 由辽宁省食源性病原性微生物快速检测与安全控制中心提供;牛奶 市售纯牛奶，购于大连本地超市;胰酪胨大豆琼脂培养基 青岛高科园海博生物技术有限公司。

MLS－3780高压蒸汽灭菌器 三洋电机株式会社;海尔hrcj－1D超净工作台 青岛海尔特种电器有限公司;DNP－9052电热恒温培养箱 上海精宏实验设备有限公司;海尔HYC－326A医用冷藏箱 青岛海尔特种电器有限公司。

1.2 实验方法

1.2.1 样品处理 将35℃活化15h后处于对数生长期的单增李斯特菌接种于纯牛奶(50mL牛奶/250mL三角瓶)中，使初始接种量达到3×103CFU/mL，考虑到牛奶常见贮藏温度和建模均匀取值需要，将牛奶样品分别放置于5、15、25和35℃恒温冷藏箱和恒温培养箱中贮藏，根据实验设计每隔一定时间取样测定细菌总数。

1.2.2 细菌总数测定 无菌操作吸取样品各5mL，分别放入装有灭菌生理盐水的三角瓶中，适当稀释，涂布于胰酪胨大豆琼脂培养基表面，36℃培养24h，采用平板计数法测定各样品中的细菌总数［9］。

1.2.3 生长动力学模型(初级模型)的建立 利用在5、15、25和35℃条件下测得的生长曲线实验数据分别拟合 Gompertz 方程［10］、Logistic 方程［10－11］和 Hill方程［12］，建立相应的模型，并确定最优的初级模型。

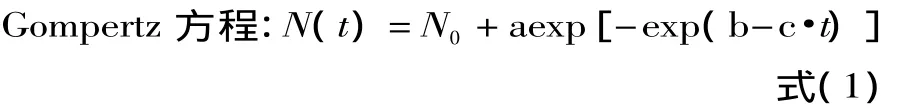
式中，t为时间，h;N(t)为t时的菌数，lg(CFU/mL);N0为初始菌数，lg(CFU/mL);a、b和 c为待定系数。

式中，t为时间，h;N(t)为t时的菌数，lg(CFU/mL);N0为初始菌数，lg(CFU/mL);a、b和 c为待定系数。

式中，t为时间，h;N(t)为t时的菌数，lg(CFU/mL);N0为初始菌数，lg(CFU/mL);a、b和 c为待定系数。

1.2.4 温度对微生物影响的动力学模型(二级模型)的建立 利用最优初级模型(Gompertz方程)中的实验数据来建立温度对单增李斯特菌影响的二级模型。二级模型采用Belehradek方程，是由Ratkowsky等［13］根据微生物在0～40℃条件下，最大生长速率或延滞时间倒数的平方根与温度之间存在的线性关系而提出的经验模型。

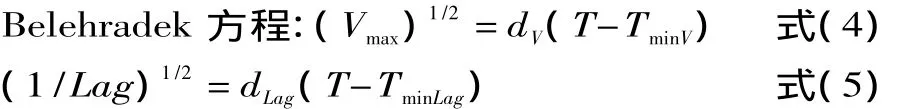
式中，T为温度，℃;Vmax为温度T时的最大生长速率，h－1;Lag为温度 T 时的延滞时间，h;dV、dLag、TminV和TminLag均为待定系数，其中 TminV和 TminLag为假定的微生物生长的最低温度，℃。

根据Gompertz方程可推导出［14］:最大生长速率:Vmax=ac/e;延滞时间:Lag=(b－1)/c;最大菌数:Nmax=N0+a。

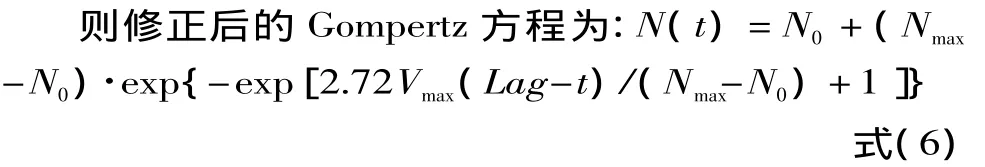
1.2.5 生长预测模型的验证与可靠性评价 应用建立的单增李斯特菌生长动力学模型来求得20℃条件下预测值，与实测值进行比较，并采用偏差度和准确度来评价预测模型的可靠性［15］。

式中，N预测为生长模型的预测值，lg(CFU/mL);N实测为同一时间的实测值，lg(CFU/mL);n为实验次数。

1.3 数据处理

实验结果为三次重复的平均值，采用SAS 8.2进行实验数据的统计与分析，采用Statistica 6.0进行模型的拟合。

2 结果与分析

2.1 单增李斯特菌的生长动力学曲线和拟合的初级模型

将牛奶在5、15、25和35℃贮藏过程中得到的细菌总数值，分别采用Gompertz方程、Logistic方程和Hill方程进行拟合，得到的生长曲线如图1所示。

由表 1可知，在 5、15、25和 35℃ 条件下Gompertz方程拟合的模型 R2均大于同温度下Logistic方程和Hill方程拟合的模型，且Gompertz方程拟合模型的标准误差(SE)均小于其它两种模型，这表明Gompertz方程拟合的模型更接近于真实值，因此选择Gompertz方程作为单增李斯特菌在牛奶中的最优初级模型，并以此为基础建立二级模型。

2.2 温度对单增李斯特菌影响的动力学模型(二级模型)

表2为不同温度条件下Gompertz方程拟合的生长动力学模型的各项参数。随着温度的升高，最大菌数(Nmax)和最大生长速率(Vmax)逐渐变大，而延滞时间(Lag)则逐渐缩短。最大生长速率或延滞时间倒数的平方根与温度之间存在的线性关系，需要采用Belehradek方程进行描述。

由图2可知，最大生长速率(Vmax)和延滞时间(Lag)倒数的平方根与温度之间存在的良好的线性关系，模型的 R2分别为 0.9721和0.9747，这表明Belehradek方程更好的描述了不同温度变化对单增李斯特菌生长的影响。温度与最大生长速率和延滞时间的Belehradek方程分别为:

图1 单增李斯特菌在不同温度条件下的生长曲线和动力学模型Fig.1 Growth curves and kinetic models of L.monocytogenes at different temperature

表1 不同温度条件下单增李斯特菌在牛奶中的生长动力学模型Table 1 Growth kinetics models of L.monocytogenes in milk at different temperatures

表2 单增李斯特菌在牛奶中生长动力学模型的参数Table 2 Parameters of growth kinetics model of L.monocytogenes in milk

图2 温度与最大生长速度和延滞时间的关系Fig.2 Relationship between temperature and Vmaxor Lag

由最大生长速度和延滞时间的实测值与预测值的残差分析(表3)可知，残差值均小于0.06，这表明Belehradek方程建立的二级模型是可信的。

表3 温度与最大生长速度和延滞时间平方根模型的残差分析Table 3 Residuals analysis of temperature and(Vmax)1/2or(1/Lag)1/2

表4 20℃条件下单增李斯特菌生长预测模型的验证与分析Table 4 Verification and analysis of growth kinetics prediction model of L.monocytogenes at 20℃

2.3 单增李斯特菌生长预测模型的验证与可靠性评价

为验证建立的生长预测模型的有效性和可靠性，根据预测模型构建20℃条件下单增李斯特菌的生长动力学方程，比较同一时间的预测值和实测值，并分析预测模型的偏差度和准确度。采用李苗云等［9］和李除夕等［15］最大菌数的计算方法，20℃ 条件下最大菌数(Nmax)以15℃和25℃条件下最大菌数对数值的平均值为判断指标，由二级模型(Belehradek方程)计算出20℃时的最大生长速率(Vmax)和延滞时间(Lag)，带入修正后的Gompertz方程，求得20℃条件下单增李斯特菌的生长预测模型(初级模型)为:

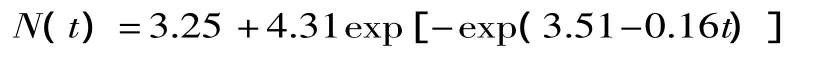
由表4可知，20℃条件下生长预测模型的残差值均小于0.2，偏差度为1.04，准确度为1.13，小于李除夕等建立的豆腐中库特氏菌生长预测模型的偏差度和准确度［15］，表明建立的模型有效且可靠，在已知初始菌数(N0)的情况下，可以快速预测5～35℃条件下不同贮藏时间点时单增李斯特菌在牛奶中的生长情况。

3 结论

比较了5、15、25和35℃条件下Gompertz方程、Logistic方程和Hill方程对单增李斯特菌在牛奶中生长动力学曲线的拟合情况，确定Gompertz方程为最优的初级模型。在此基础上，采用Belehradek方程建立了相应的二级模型。验证实验结果为:20℃条件下单增李斯特菌细菌总数的预测值和真实值的残差均小于0.2，模型的偏差度为1.04，准确度为1.13，这表明建立的模型有效且可靠。在已知初始菌数的情况下，可以根据模型快速预测5～35℃条件下不同贮藏时间点时单增李斯特菌在牛奶中的生长情况。本研究结果对预测和监控食源性致病菌在食物中的生长和繁殖，保证食品的安全性等方面具有参考价值。

［1］Jadhav S，Bhave M，Palombo EA.Methods used for the detection and subtyping of Listeria monocytogenes［J］.Journal of Microbiological Methods，2012，88:327－341.

［2］Donaldson JR，Nanduri B，Pittman JR，et al.Proteomic expression profiles of virulent and avirulent strains of Listeria monocytogenesisolated from macrophages［J］.Journalof Proteomics，2011，74:1906－1917.

［3］Shahbana SA，Manjulab N，Siddiqui S.Listeria septicaemia following insertion of a dynamic hip screw:A case report and literature review［J］.International Journal of Surgery Case Reports，2012，3:448－450.

［4］Arif M，Rajpoot NM，Nattkemper TW，et al.Quantification of cell infection caused by Listeria monocytogenes invasion［J］.Journal of Biotechnology，2012，154:76－83.

［5］丁甜，董庆利，相启森，等.Listeria monocytogenes在经高氧化还原电位酸性水处理的鲜食莴苣上预测模型的建立［J］.食品工业科技，2010，31(3):87－90，94.

［6］Cava－Roda RM，Taboada A，Palop A，et al.Heat resistance of Listeria monocytogenes in semi－skim milk supplemented with vanillin［J］.International Journal of Food Microbiology，2012，157(2):314－318.

［7］McMeekin T，Bowman J，McQuestin O，et al.The future of predictive microbiology:Strategic research，innovative applications and greatexpectations［J］.InternationalJournalofFood Microbiology，2008，128(1):2－9.

［8］Mertens L，Derlinden EV，Impe JFV.Comparing experimental design schemes in predictive food microbiology:Optimal parameter estimation of secondary models［J］.Journal of Food Engineering，2012，112:119－133.

［9］李苗云，孙灵霞，周光宏，等.冷却猪肉不同贮藏温度的货架期预测模型［J］.农业工程学报，2008，24(4):235－239.

［10］Zwietering MH，JongenburgerI，Rombouts FM，et al.Modeling of the bacterial growth curve［J］.Applied and Environmental Microbiology，1990，56(5):1875－1881.

［11］李博，满朝新，赵凤，等.原料乳中金黄色葡萄球菌生长预测模型的建立［J］.食品科学，2011，32(15):158－162.

［12］王怀记，王增珍.Hill模型及其在环境危险度评价中的应用［J］.中国卫生统计，2006，23(4):372－374.

［13］Ratkowsky DA，Olley J，McMeekin TA，et al.Relationship between temperature and growth rate of bacterial cultures［J］.Journal of Bacteriology，1982，149(1):1－5.

［14］刘超群，陈艳丽，王宏勋，等.冷鲜猪肉中热杀索丝菌生长预测模型的建立与验证［J］.食品科学，2010，31(18):86－89.

［15］李除夕，董明盛，陈晓红，等.豆腐中库特氏菌生长动力学模型和货架期预测［J］.农业工程学报，2009，25(1):82－86.