危岩破坏激振信号局部和细节信息特征

陈洪凯，杨 铭，唐红梅，何晓英，王 智

（1.三峡大学水利与环境工程学院，湖北宜昌 443002；2.重庆交通大学岩土工程研究所，重庆 400074）

危岩破坏激振信号局部和细节信息特征

陈洪凯1，2，杨 铭1，唐红梅2，何晓英2，王 智2

（1.三峡大学水利与环境工程学院，湖北宜昌 443002；2.重庆交通大学岩土工程研究所，重庆 400074）

危岩属于一种突发性地质灾害，危岩破坏会突然释放能量，以激振波的形式向邻近危岩块传递，劣化相邻危岩体的稳定性。通过坠落式危岩破坏激振效应模型试验，对采集的激振信号进行小波滤噪处理，选取模型试验第25～35 ms共10ms时间段的激振信号，作为分析激振信号局部和细节信息特征的基础数据。分析结果表明，实验条件下分析时段内，危岩破坏激振信号局部信息存在周期性，激振信号在水平方向存在8～9个激振峰，周期1.0～1.4 ms，在竖直方向存在3～4个激振峰，周期2.2～3.0 ms；测点与激振源之间的距离影响着激振信号的峰值强度，距离越近，峰值强度越大；危岩块之间界面的完整性对激振信号出现频率和峰值强度都有显著影响，激振信号穿过不完整的界面后激振信号主峰存在一定滞后性，实验条件下滞后时间10ms左右；危岩破坏激振信号的局部和细节信息基本都在细节系数中予以体现，尤其是主频率主要位于d3～d7所对应的中频细节信息内。研究成果对于进一步实施危岩破坏激振效应的相似模型试验具有积极意义。

危岩破坏；激振信号；局部信息特征；细节信息特征；室内模型试验

危岩崩塌（perilous rock and collapse）是我国山区主要地质灾害类型，具有泛生性、突发性、强致灾等特征，严重威胁着山区公路铁路交通运输、城镇居民以及矿山开采安全。国土资源部2012年发布的全国地质灾害通报表明，近十年来我国平均每年产生崩塌灾害2 000次以上，如2010年发生5 575起、2011年发生2 319起，占发生地质灾害总数的30～40%，直接经济损失超过13亿元/年。初步研究表明，危岩破坏会突然释放能量［1］，产生激振效应（excitation effect），并以激振波的方式向相邻危岩块传递［2］，并劣化相邻危岩块的稳定性［3］。模型试验是探索危岩破坏激振效应的重要科学途径之一，针对坠落式危岩破坏激振效应模型试验量测的初始激振信号［4］（初始激振加速度），为了确保初始激振信号的科学性，需对其进行滤噪处理。Morlet［5］提出了小波变换方法，克服了短时Fourier变换在单分辨率上的缺陷，在时域和频域上均能表征信号的局部信息［6］，尤其可有效刻画诸如危岩破坏激振信号中的瞬态成分［7－8］；Donoho等［9］提出了用于处理小波系数的软阈值函数和硬阈值函数；陈洪凯等［10］发现硬阈值法对于泥石流、危岩等地质灾害突发性冲击信号的滤噪处理具有明显优势；赵翔等［11］的研究也表明，Daubechies（dbN）小波系列具有较好的紧支持性、光滑性及近似对称性，可用于分析振动信号，目前常用db5和db8小波基。为了深入研究激振效应对危岩破坏过程的激化作用，本文针对所实施的坠落式危岩破坏激振效应模型试验［4］，采用小波硬阈值法对实验采集的初始激振信号进行滤噪处理和小波分解，据此探索实验条件下危岩破坏激振信号的局部信息和细节信息特征。研究成果对于进一步实施危岩破坏激振效应相似模型试验研究具有积极意义。

1 危岩破坏激振效应模型试验

针对坠落式危岩（falling perilous rock），建造试验模型如图1所示，包括四层危岩体，每层危岩体厚30 cm，并被两列主控结构面分割成三个危岩体，如第一层危岩体在第1列主控结构面外侧的为第11＃危岩块，第1和第2列主控结构面之间的为第12＃危岩块，第2列主控结构面后侧为第13＃危岩块。布置了三个加速度传感器测点（图2），其中1＃测点布置在第12＃危岩块中部，2＃测点布置在第13＃危岩块中部，3＃测点布置在第22＃危岩块中部。模型试验时，第11＃危岩块为起崩块（崩塌源）。该模型试验重点关注起崩块在主控结构面内安防静态爆破剂后突发性崩落瞬间在1＃、2＃和3＃测点所采集的激振信号，用激振加速度表征，所采集试验数据有13万余个［4］。

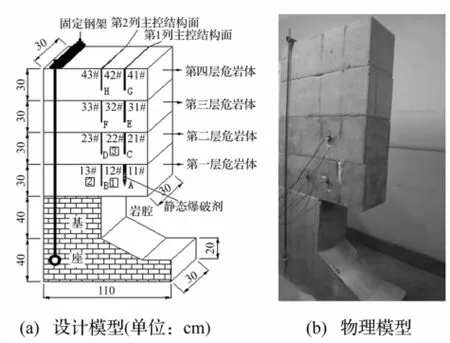
图1 危岩破坏激振效应试验模型Fig.1 Experimentalmodel of excitation effect for perilous rock to rupture

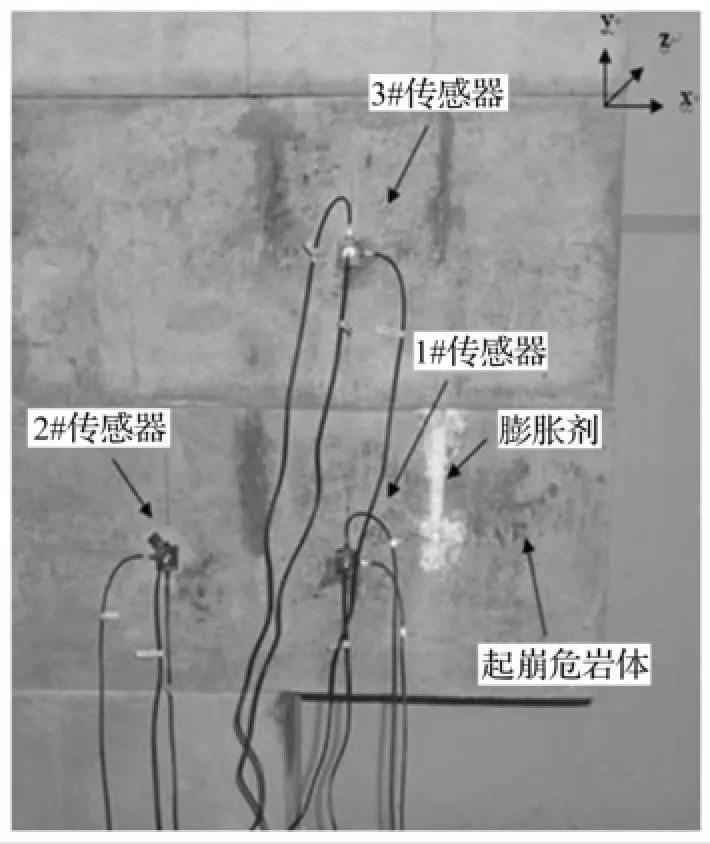
图2 试验模型上传感器布置方案Fig.2 Arrangementof sensors on experimentmodel

2 试验结果分析

2.1 激振信号局部信息特征

为了探索危岩破坏激振信号的微观特性，采用小波理论硬阈值法［10］对危岩破坏模型试验采集的初始激振信号（激振加速度）进行滤噪处理，由于模型试验记录的时间为0～55 ms，其中第20～50 ms出现明显的激振效应［4］，本文选取试验过程第25～35 ms共10 ms时间段1＃、2＃和3＃测点记录的激振加速度作为分析对象，基本消除了试验初始段和结束段激振信号的不稳定问题。1＃、2＃和3＃测点激振信号水平方向的局部时程曲线如图3所示，竖直方向的局部时程曲线如图4所示，图中虚线代表信号比较示踪线，实线代表激振信号变化曲线。

从图3和图4可看出实验条件下危岩破坏激振信号局部信息具有如下特征：

（1）由于危岩属于脆性破坏，所释放的能量具有突发性［1］，所产生的激振波局部信息存在一定周期性，可定义为激振信号强度峰值出现的时间间隔，而将单位时间内出现的激振峰数量定义为激振频率。激振信号在水平方向的激振频率大于竖直方向的激振频率，如图3显示1＃测点和2＃测点激振信号在水平方向存在9个峰，但第9个峰在3＃测点消失；图4显示1＃测点和2＃测点激振信号在竖直方向存在4个峰，但第4个峰在3＃测点消失。峰越多，表明激振频率越大，由相邻激振信号峰之间的间隔时间表征的激振作用周期越短，水平方向激振信号的周期为1.0～1.4 ms，竖直方向增大到2.2～3.0 ms。

（2）对于激振信号在水平方向的峰值强度，1＃测点为29.5 m/s2，2＃测点为22.7 m/s2，3＃测点为21.2 m/s2，而在竖直方向的峰值强度，1＃测点为30.5 m/s2，2＃测点为24.1 m/s2，3＃测点为20.4 m/s2。表明测点与激振源之间的距离影响着激振信号的峰值强度，距离越近，激振能量衰减越慢，如水平方向1＃测点的激振信号峰值强度便是2＃测点的1.30倍。

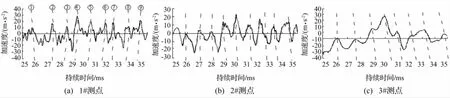
图3 激振信号水平方向（x方向）局部时程曲线Fig.3 Local time-history curve of excitation signal at x direction

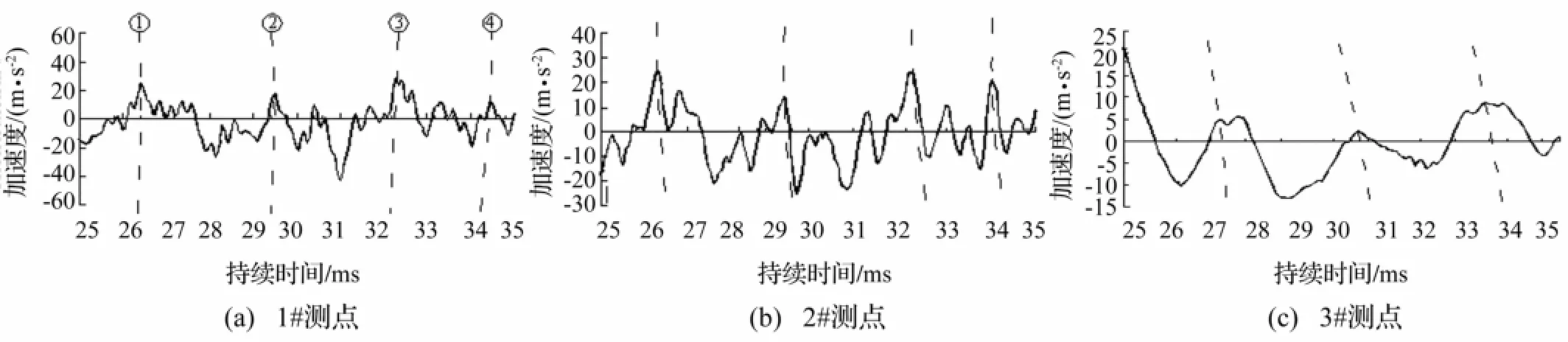
图4 激振信号竖直方向（y方向）局部时程曲线Fig.4 Local time-history curve of excitation signal at y direction

（3）危岩块之间界面的完整性对激振信号的影响是比较显著的，主要表现在激振信号出现频率和峰值强度两方面。由于第12＃危岩块和第13＃危岩块之间的界面（主控结构面）上部分贯通、下部分完整，而第12＃危岩块和第22＃危岩块之间的界面则属于接触比较紧密的不连续面，从激振信号出现频率来看，3＃测点量测到的激振信号频率明显小于2＃测点量测到的激振信号频率，从激振信号峰值示踪线发现，3＃测点所记录的激振信号主峰出现时间明显有滞后性，滞后时间10 ms左右。从激振信号峰值强度角度，在水平方向，3＃测点峰值强度仅为1＃测点的0.38倍，而2＃测点可及0.77倍；在竖直方向，3＃测点峰值强度是1＃测点的0.67倍，而2＃测点提高到0.79倍。

2.2 激振信号细节信息特征

由于小波理论中db小波函数具有阶数越高规则性越强的特征，为了精细地观测危岩破坏激振信号的细节特性，采用db8小波对激振信号S进行8层一维多尺度分解［5］：

S＝a8＋d8＋d7＋d6＋d5＋d4＋d3＋d2＋d1（1）式中：a为近似系数；d为细节系数，其序号数表示小波分解的层树（尺度数）。

由式（1）将分解后的激振信号进行重构，以1＃测点竖直方向的激振信号为例，其小波分解近似系数和细节系数重构信息如图5所示。

从图5可看出实验条件下危岩破坏激振信号竖直方向细节信息具有如下特征：

（1）危岩破坏激振信号采用db8小波函数分解后，由一个近似系数a8和d1～d8共8个细节系数组成。近似系数a8的周期采用相邻激振峰之间的间隔时间表征，约27ms，但振幅仅为1.12 m/s2。近似系数a8垂直向下的振幅最大值可及1.31 m/s2，而任何一层细节系数均高于该幅值。表明危岩破坏激振信号的信息通过db8分解后基本都在细节系数中予以体现，进一步分析细节系数所携带的相关信息对于科学认识危岩破坏激振信号特性有重要意义。

（2）据小波理论，db8小波细节系数中，d1和d2代表高频信息，d3～d7代表中频信息，d8代表低频信息。信号频率影响着细节系数的出现时间，频率越高，细节系数出现时间越晚，如d1细节系数出现时间为第19.5 ms，d2细节系数出现时间为第19 ms，d3细节系数出现时间为第18.5 ms，d4细节系数出现时间为第18ms，d5细节系数出现时间为第15 ms，d6细节系数出现时间为第8 ms，d7细节系数出现时间为第2 ms，d8细节系数出现时间与危岩破坏激振试验过程基本同步。

（3）危岩破坏激振信号d1～d8细节系数中，从低频到高频，细节系数存在明显波动性，但波动周期及其振幅大小存在显著差异，如低频信息d8细节系数周期为12 ms、振幅为1.9 m/s2，中频信息d6细节系数周期为4 ms、振幅为15.3 m/s2，d5细节系数周期为2.5 ms、振幅为14.1 m/s2，高频信息d1细节系数周期仅为0.003 ms、振幅降低到3.7 m/s2。由于激振信号的低频信息db8细节系数具有持续时间长而振幅低、高频信息d1和d2细节系数具有持续时间短而振幅小的特点，其携带的能量均较小，可能属于模型试验过程中量测到的噪声信号，显然，危岩破坏激振信号的主频率位于d3～d7所对应细节信息内。

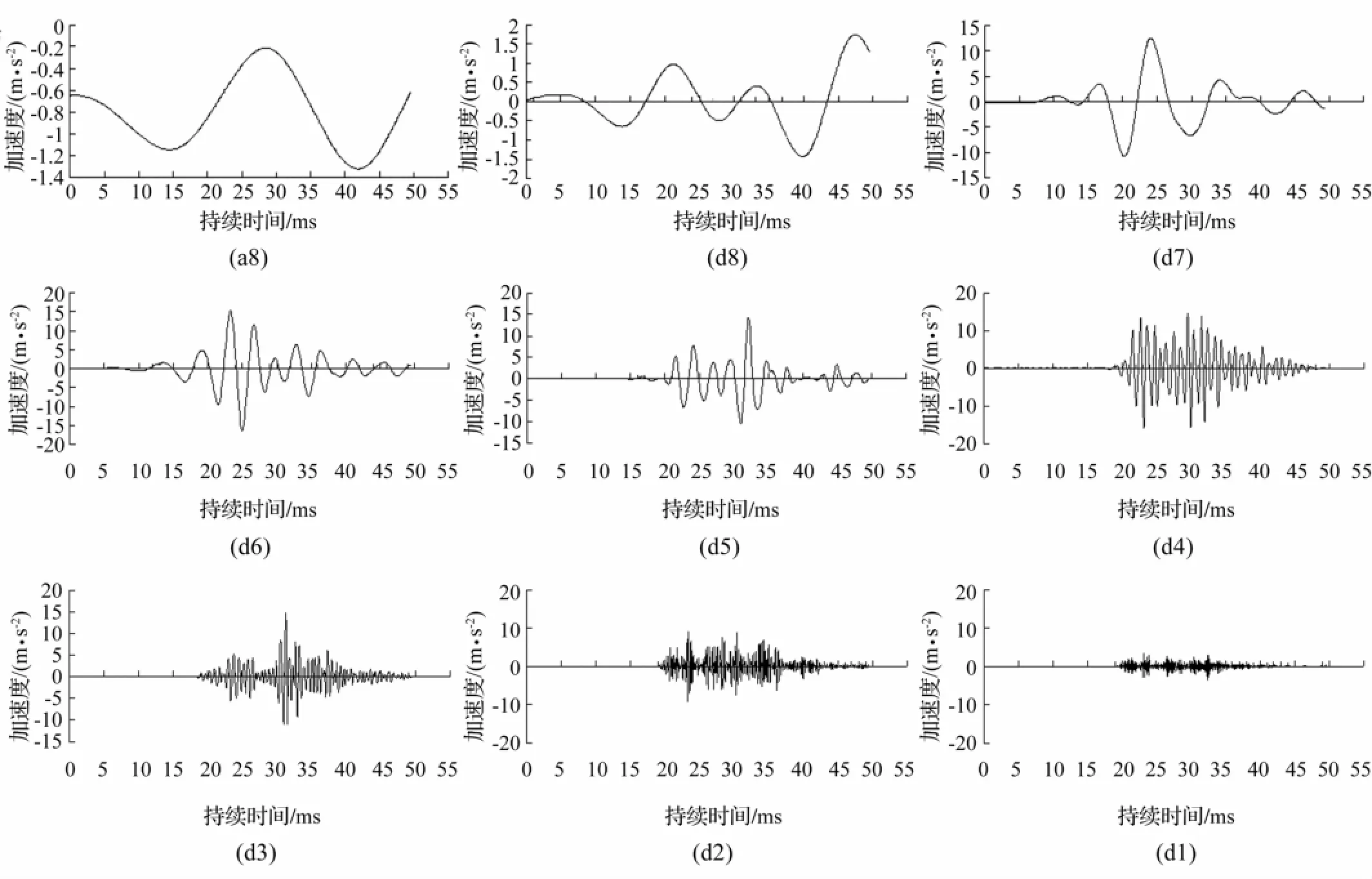
图5激振信号竖直方向（y方向）小波分解近似系数和细节系数重构时程曲线Fig.5 Time-history curve of excitation signal at y direction with approximate coefficients and m inutiae coefficients decompounded by waveletmethod

3 结 论

危岩破坏会突然释放能量，以激振波的形式向邻近危岩块传递，激振信号主要采用激振加速度表征。针对坠落式危岩破坏激振效应模型试验提取的激振信号，通过小波硬阈值法滤噪处理，提取出能较客观地表征危岩破坏激振效应的激振信号，并分析其局部信息和细节信息特征，取得如下主要结论：

（1）从滤噪处理后的激振信号中，选取模型试验第25～35 ms共10 ms时间段的激振信号，作为分析激振信号局部信息特征的基础数据，具有代表性。激振波的激振信号局部信息具有一定周期性，且在水平方向的激振频率大于竖直方向的激振频率，实验条件下前者存在8～9个激振峰，周期1.0～1.4 ms，后者存在3～4个激振峰，周期2.2～3.0 ms。

（2）测点与激振源之间的距离明显影响着激振信号的峰值强度，距离越近，激振能量损失越小，峰值强度越大，并且竖直方向激振信号的峰值强度大于水平方向激振信号的峰值强度；危岩块之间界面的完整性对激振信号出现频率和峰值强度都有显著影响，不完整的界面，激振信号主峰存在一定滞后性，滞后时间10 ms左右。

（3）危岩破坏激振信号的信息通过db8分解后基本都在细节系数中予以体现，激振信号d1～d8细节系数存在波动性，从低频到高频激振信号细节系数出现时间越晚，激振波主频率主要位于d3～d7所对应的中频细节信息内。

进一步研究中，应针选取具有现场观测资料的实际危岩体进行室内相似模型试验，分析实际危岩破坏的激振效应问题，为科学验证危岩激振效应理论解提供科学依据。

［1］陈洪凯，张瑞刚，唐红梅，等.压剪型危岩破坏弹冲动力参数研究［J］.振动与冲击，2012，31（24）：30－33.

CHEN Hong-kai，ZHANG Rui-gang，TANG Hong-mei，et al.Elastic＆impulsive dynamic parameters of a ruptured compression-shear perilous rock［J］.Journal of Vibration and Shock，2012，31（24）：30－33.

［2］唐红梅，王智，陈洪凯，等.坠落式危岩崩落的激振效应与求解［J］.振动与冲击，2012，31（20）：32－37.

TANG Hong-mei，WANG Zhi，CHEN Hong-kai，et al.Contribution ratio of excitation action triggered by collapse of perilous rock to stability of perilous rock［J］.Journal of Vibration and Shock，2012，31（20）：32－37.

［3］唐红梅，王智，鲜学福，等.坠落式危岩剧动式崩落与激振效应［J］.重庆大学学报，2011，34（10）：39－45.

TANG Hong-mei，WANG Zhi，XIAN Xue-fu，et al.Violentslide rock avalancheand excitation effectof perilous rock［J］.Journal of Chongqing University（Natural Science Edition），2011，34（10）：39－45.

［4］唐红梅，陈洪凯，王智，等.危岩破坏激振效应试验研究［J］.岩土工程学报，2013，35（11）：2117－2122.

TANG Hong-mei，CHEN Hong-kai，WANG Zhi，et al.Experimental study on excitation effect for unstable rock［J］.Chinese Journal of Geotechnical Engineering，2013，35（11）：2117－2122.

［5］Morlet J.Wave propagation and sampling theory［J］.Grophys.，1982，47（2）：203－236.

［6］Daubechies I.Orthonormal bass of compactly supported wavelets［J］.Commun Pure Appl.Math，1988，41（7）：909－996.

［7］董长虹，高志，余啸海.Matlab小波分析工具箱原理与应用［M］.北京：国防工业出版社，2004.

［8］Stephanem，Wenl.Singularity detection and processing with wavelet［J］.IEEE Trans on Information Theory，1992，38（2）：617－643.

［9］Donoho D L，Johostone IM.Adapting to unknow smoothness by wavelet shrinkage［J］.Journal of The American Statistical Association，1995，90（432）：40－80.

［10］Chen Hong-kai，Tang Hong-mei，Zhang Yu-ping，et al.Waveletmethod to extract shock signal of debris flow［J］.Advanced Materials Research，2011，vols.199－200：958－965.

［11］赵翔，梁开水，张志旭.水泥矿山中深孔爆破震动信号频谱特征分析［J］.武汉理工大学学报，2006，28（12）：82－84.

ZHAO Xiang，LIANG Kai-shui，ZHANG Zhi-xu.Spectra characteristics analysis of medium-to-deep holes blasting vibration signal in limestone mine［J］.Journal of Wuhan University of Technology，2006，28（12）：82－84.

Local and m inutiae characteristics of excitation signals during perilous rock rupture

CHEN Hong-kai1，2，YANGMing1，TANGHong-mei2，HE Xiao-ying2，WANG Zhi2
（1.College of Hydraulic＆Environmental Engineering，China Three-Gorge University，Yichang 443002，China；
2.Institute of Geotechnical Engineering，Chongqing Jiaotong University，Chongqing 400074，China）

As one of emergency geological disasters，perilous rock releases abruptly energy during rupture.The energy passes through perilous rock blocks near the rupture position in the form of excitation wave，and it decreases the stability of perilous rocks near the rupture position.Here，by de-noising processing with the waveletmethod of excitation signals gathered in amodel test of falling perilous rock rupture in laboratory，the signals during 10 ms duration from the 25 ms to 35ms in themodel test were taken as the essential data to analyze local and minutiae characteristics of excitation signals during perilous rock rupture.Under the test conditions，analysis results showed that local characteristics of excitation signals during perilous rock rupture have a certain periodicity，i.e.，8 or9 excitation peakswith 1.0～1.4ms periods exist in horizontal direction，while 3 or 4 excitation peaks with 2.2～3.0 ms periods in vertical direction；the distance between the measuring point and the rupture position significantly affects the amplitude of excitation peaks，the closer the distance，the bigger the amplitude；furthermore，the integrity of the interface between two perilous rock blocks has a significant impact on the frequency and amplitude of excitation peaks，when an excitation signal passes through an incomplete interface，the peaks of the excitation signal are lagged a little，the time-delay is about10 ms under the tests；specially，almost all local and minutiae characteristics of excitation signals during perilous rock rupture can be embodied with minutiae coefficients，themain frequency of excitation signals appear in minutiae characteristics from d3 to d7.Achievements gained here were helpful for implementation of similarmodel tests of excitation effect during perilous rock rupture.

perilous rock rupture；excitation signal；local characteristics；minutiae characteristics；model test in laboratory

P642.21；P642.3

A

10.13465/j.cnki.jvs.2014.24.003

国家自然科学基金（11272185，51378521）；2013年重庆高校创新团队建设计划资助项目（KJTD201305）；重庆市“两江学者”计划专项经费资助

2013－08－15 修改稿收到日期：2014－01－09

陈洪凯男，博士后，教授，博士生导师，1964年生

唐红梅女，博士，研究员，1968年生