金属大变形过程中温度场的Abaqus模拟

马 璇

（沈阳师范大学 物理科学与技术学院，沈阳 110034）

0 引 言

热轧过程是典型的金属大变形过程之一。在这一过程中，轧件在高温下发生变形，由于轧件内部温度分布和组织形式的不均匀，而形成了热应力和相变应力，当这些应力达到材料的屈服极限时，必定会在一定程度上造成局部塑性变形，从而影响轧件的最终性能和使用寿命。如果处理不当，可能会造成轧件组织性能不达标，更严重的会产生变形和开裂。在实际生产中，如果能提前预知温度场和应力场的分布，就会从一定程度上利用技术手段来尽量控制产生缺陷的程度。所以，研究变形过程中温度场及其分布至关重要。

利用计算机模拟技术研究金属变形过程及其内部各参数的变化，是近几年该领域常用的方法之一。计算机模拟技术能够将变形中的物理现象和变形过程有机的结合在一起，从而实现变形过程中的动态模拟。特别是有限元思想的提出，为复杂问题简单化提供了理论依据。有限元方法求解问题的基本步骤通常为：问题及求解域定义，求解域离散化，确定状态变量和控制方法，单元推导。Abaqus是功能强大的基于有限元方法的工程分析软件，其分析步骤主要包括前处理、分析计算和后处理。特别是该软件能自动处理非线性边值问题，大大减少了计算人员的工作强度。本文利用Abaqus软件，构建实际轧件模型，加以适当的载荷，并结合实验获得的相关数据，真实的模拟了轧件的形状和定解条件，得到了动态的温度场分布。

1 有限元求解的条件

有限元方法在模拟金属变形过程中，有其独有的优势，结合热传导和导热的边界条件，能使模拟结果更接近实际情况。考虑到金属在轧制过程中，会在空气和轧辊之间发生热传递，所以把以下2个方程设定为求解条件。

1.1 热传导偏微分方程

平面二维热传导的偏微分方程［1］为：

式中，T为瞬态温度；t为时间；k为导热系数；ρ为金属密度；cp为定压比热；q为内热源强度；x和y分别表示宽度和厚度方向的直角坐标。

1.2 导热的边界条件

在已知环境温度和换热系数的情况下，边界条件为［2］：

式中，h为换热系数；T∞为环境温度。

2 温度场数学模型的建立

2.1 轧件内部温度场的数学模型

轧制过程中，轧件内部主要有以下几种热现象［2，5］：

1）变形热

变形热主要是金属的塑性变形引起的，其表达式为：

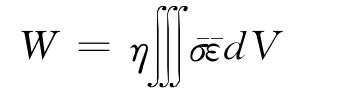
式中，¯ε为平均变形速率；¯σ为等效应力；η为塑性功转变为热的比例，在此可以取0.7～0.9。

2）摩擦热

摩擦热是由金属和轧辊之间的摩擦产生的，其表达式为：

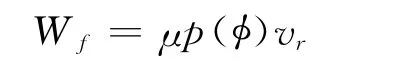
式中，μ为摩擦系数；p（φ）为轧制压力的法向分量；vr为相对速度的绝对值。

3）接触热

在接触面上的接触热，是热流连续而温度不连续的热阻问题，所以热交换系数h为：

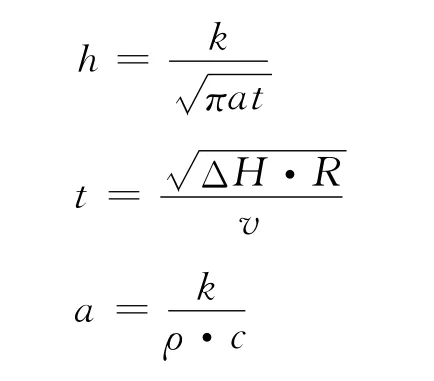
式中，t为接触时间；v为轧制速度；ΔH为形变量。

2.2 轧件空冷和水冷过程中的数学模型

1）空冷过程数学模型

在空冷过程中，考虑到对流和辐射的综合影响，可以换算出一个综合的换热系数

式中，hc为自然对流换热系数；s为Stefan－Boltzmann常数；ε为材料表面的辐射率；T为轧件表面温度；T∞为环境温度。

2）水冷过程数学模型

水冷过程中，换热系数受到设备条件、冷却水量等因素的影响，结合以前的研究成果［11－12］，可以总结出以下的表达式：

式中，μcp为动力粘度；λ为导热系数；Re为雷诺数；W为冲击区宽度。

3 温度场的有限元模型

3.1 物性参数的确定

对于金属而言，物性参数是随着温度变化的，对模拟的结果影响很大［3－4］。所以，在计算之前，一定要确定所需的必要物性参数。其中导热系数、比热、热导率能够通过热模拟实验来确定，其结果见表1。弹性模量和泊松比也可以通过实验测量，其结果见表2。

表1 材料导热系数、比热和热导率

表2 材料杨氏模量和泊松比

3.2 物理模型的建立

由于本文只考虑轧件纵向剖面的温度场分布，所以建立的是二维有限元模型（见图1）。该模型中设定轧件为长1 200mm，厚40mm的可变形体，轧辊为半径866mm的环状可变形体。轧件和轧辊的网格都为四边形网格，采用自由技术和进阶算法。轧件和轧辊之间的接触设为面－面接触，设轧件和轧辊间的摩擦系数为0.3，分析过程采用动态显示分析方法，考虑热力耦合，并且设定轧件的底面为对称边界条件。

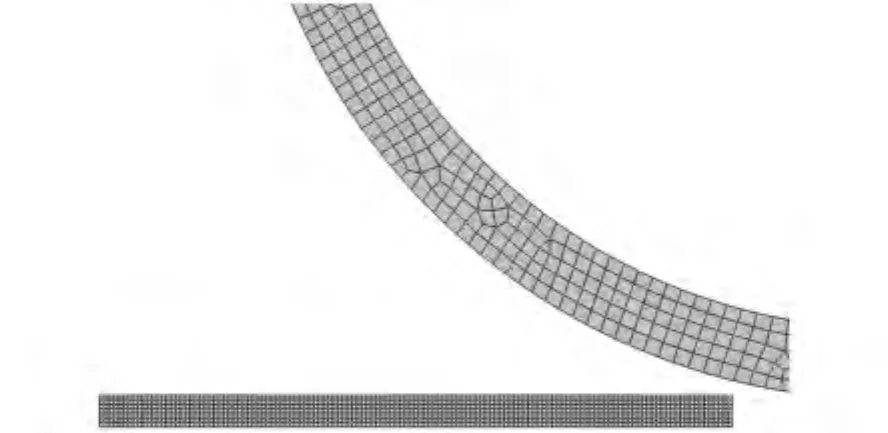
图1 二维有限元模型

4 模拟结果及分析

经过Abaqus软件的模拟，得出金属变形过程中的温度场分布（见图2）。

图2 温度场的模拟结果

图3中所示的表面温度（Surface）是指轧件外表面温度，中心温度（Center）是指轧件的中心温度。从图中可以看出，轧件表面温度随着轧制过程的进行逐渐减小。在开始轧制时，由于轧辊和轧件接触，轧辊的温度较低，轧件的温度较高，会在轧件表面和轧辊表面发生热传导，从而使轧件表面温度降低。但是，随着轧制的进一步进行，在轧制变形区，轧件表面温度略有回升。出现这种现象，主要是由于在该区域产生了变形热，所以说明变形热对轧件的温度也会产生一定的影响。而轧件的中心温度在轧制过程中基本保持不变，只是在轧制后期有小幅度的下降，这主要是随着轧制过程的进行，轧件厚度逐渐减小，对外界的热传导更加容易，温度降低更明显。

图3 变形过程中温度曲线

5 结 论

本文借助Abaqus有限元仿真软件，模拟了金属轧制过程中的温度场分布，从模拟结果可以看出：

1）热变形过程中，变形金属与环境温度的热交换是不能忽视的，这在一定程度上影响着金属表面的温度分布。但是如果轧件温度非常高，会对环境温度产生影响，所以在设定初始环境温度时，可以把温度设的略高一点。

2）金属与外界接触的接触面与外界发生热交换，交换的热量与温度和换热系数有关。这种热交换是非稳态问题，要考虑热流连续、温度不连续的问题。

3）金属的变形热在温度场分布中表现的很明显。金属发生塑性变形时，其内部的分子运动速度显著增加，同时，金属又处在高温环境下，更加速了分子运动。分子运动加剧 ，必然会增加金属变形区的温度。这一区域是缺陷最容易产生的区域，所以在实际应用中要格外注意。

［1］孔详谦.有限元法在传热学中的应用［M］.3版.北京：科学出版社，1998：32－34.

［2］刘相华.刚塑性有限元及其在轧制中的应用［M］.北京：冶金工业出版社，1994：38－56.

［3］LIU Zhengdong.Experiments and mathematical modeling of controlled run out table cooling in a hot rolling mill［D］.Columbia：The University of British Columbia，2001.

［4］SERAJADEH S.Prediction of temperature distribution an phase transformation on the run－out table in the process of hot strip rolling［J］.Appl Math Modell，2003，27（2）：861－875.

［5］支颖.板带钢热轧过程宏观行为与介观组织的综合模拟［D］.沈阳：东北大学，2008.

［6］DU Fengshan，WANG Minting，Li Xuetong.Research on deformation and microstructure evolution during forging of large－scale parts［J］.J Mater Process Technol，2007，187：591－594.

［7］LEE H W，IM Y T.Numerical modeling of dynamic recrystallization during nonisothermal hot compression by cellular automata and finite element analysis［J］.Int J Mechan Sci，2010，52：1277－1289.

［8］张金铃，崔振山，王英杰.中厚板多道次热轧过程有限元连续模拟［J］.上海交通大学学报，2009，43（1）：65－70.

［9］何艳.材料微观组织CA法模拟的研究现状［J］.沈阳师范大学学报：自然科学版，2011，29（4）：504－509.

［10］高明，刘芳慧.相场方法在组织模拟中的应用［J］.沈阳师范大学学报：自然科学版，2013，31（3）：318－325.

［11］PACK N.Theory and applications of cellular automata［M］.Singapore：World Scientific，1986：56－73.

［12］罗伯 D.计算材料学［M］.北京：化学工业出版社，2002：98－103.