同时具有学习和恶化效应的不同工期指派问题研究

王吉波，牛玉萍，刘 璐，郭 倩

（1.沈阳航空航天大学 经济与管理学院，沈阳 110136；2.沈阳航空航天大学 理学院，沈阳 110136）

0 引 言

排序问题是一类重要的组合最优化问题，多年来人们一直在运筹学、管理科学、系统工程、计算机科学等领域致力于该问题的研究。在大多数排序问题中，工件的加工时间是一个独立的且与开工时间和加工位置无关的常数。不过，在所知的一些实际问题中，由于工人（机器）在很长的时间加工相同或类似的工件时，加工效率有可能逐渐提高，因而使得后面加工的工件的加工时间缩短，这种现象被称作具有学习效应［1］。另一方面，在实际生产中，工件的实际加工时间会因工件开始时间的推迟而延长，这种现象被称为具有恶化效应［2－3］。

Biskup［4］、Cheng等［5］首先研究了这类具有学习效应的单机排序问题。在Biskup的文章中，他证明了在具有学习效应的工件排序情况下，当目标函数为极小化共同工期偏差与完工时间和时，这类单机排序问题是多项式时间可解的。Cheng等［5］研究了工件加工时间具有学习效应的单机排序问题，其中工件的学习效应模型为一个分片线性加工时间函数，目标函数为极小化最大延误时间。他们证明了此问题是强NP－难的，并给出了2个多项式时间可解的特殊情况。同时，还提出了2个启发式算法，并分析了它们的最坏情况界。孙林辉等［6］研究了具有学习效应的流水作业排序问题，对总完工时间极小化问题，给出了数学规划模型和3个启发式算法。Mosheiov［7］对其他的一些单机排序问题进行了研究，得出了使用最小加工时间优先规则（SPT）可以获得最大完工时间问题的最优排序。Biskup［8］对这类具有学习效应的排序问题进行了综述。最近关于学习效应的排序成果，读者可参考文献［9－14］。Gawiejnowic［15］给出了关于工件具有恶化效应排序问题的综述。最近关于恶化效应的排序成果，读者可参考文献［16－19］。Lee首次提出了工件同时具有学习和恶化效应的排序问题模型［20］，接着Wang［21－28］，Low 等［29］研究了不同的模型。

王吉波等［19］研究了工件具有不同工期的排序问题，其中工件的加工时间具有恶化效应。但现实的生产过程中存在着工件加工同时具有学习效应和恶化效应的情况（Wang［21－22］，Wang等［23］），因此本文研究工件加工同时具有学习效应和恶化效应的不同工期排序问题，证明了此问题依然多项式时间可解。

1 问题模型

其中α，β和γ分别表示每一时间单元的提前、延误和工期惩罚。

2 主要结论

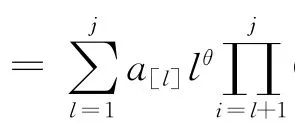
引理2 （Wang［21］）对于排序问题1｜pj＝（aj＋bt）rθ｜Cmax，最优排序能通过把工件按照aj的非减顺序排列得到（SPT规则）。

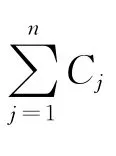
证明 令S＝（π1，Ji，Jj，π2），其中，π1和π2分别为Ji之前加工的工件和Jj之后加工的工件，Ji和Jj分别位于第r和第r＋1个位置且ai＜aj。交换第r和第r＋1个位置上的工件，其他不变，得到排序S′＝ （π1，Jj，Ji，π2）。此外，假设A为部分排序π1中最后一个任务的完工时间。为了表明序列S优于S′，需要证明 max（0，Ci（S）－d）＋max（0，Cj（S）－d）≤ max（0，C′j（S）－d）＋max（0，C′i（S）－d）。显然

因为ai＜aj，由引理2得Cj（S′）－Ci（S）＝（aj－ai）rθ＞0，即Ci（S）＜Cj（S′）Ci（S′）－Cj（S）＝（aj－ai）［rθ－（r＋1）θ＋brθ（r＋1）θ］＞0，即Ci（S′）＞Cj（S）。

下面将分6种情况进行讨论。

1）当Ci（S′）≤d时，此时Cj（S）＜Ci（S′）≤d，Ci（S）＜Cj（S）＜d，所以

2）当Ci（S）≥d时，此时Cj（S′）＞Ci（S）≥d，Ci（S′）＞Cj（S）＞d，所以

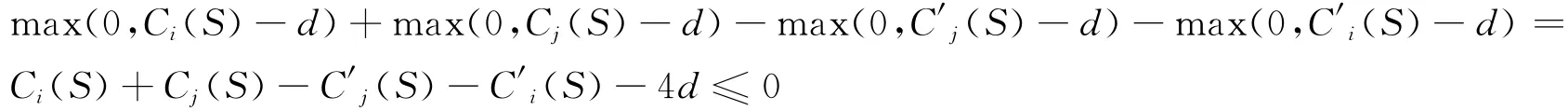
3）当Ci（S）＜d且Cj（S′）＞d，Cj（S）＜d时，此时Ci（S′）＞Cj（S′）＞d，所以

4）当Ci（S）＜d且Cj（S′）＞d，Cj（S）＞d时，此时Ci（S′）＞Cj（S）＞d，所以

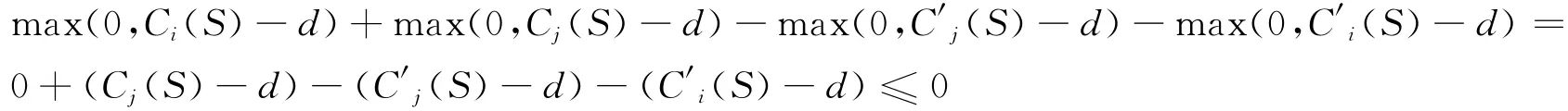
5）当Ci（S）＜d且Cj（S′）＜d，Cj（S）＞d时，此时Ci（S′）＞Cj（S）＞d，所以

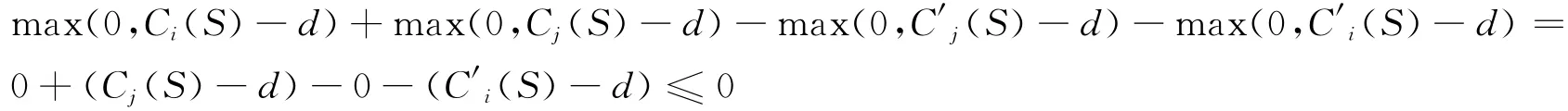
6）当Ci（S）＜d且Cj（S′）＜d，Cj（S）＜d，Ci（S′）＞d时

综上所述，可以得到当ai＜aj时，max（0，Ci（S）－d）＋max（0，Cj（S）－d）≤ max（0，C′j（S）－d）＋max（0，C′i（S）－d），即工件按照SPT规则排序可以得到最优排序。证毕。

定理1 对于任意一个给定排序π＝ （J［1］，J［2］，…，J［n］），最优排序满足如下条件：如果β≥γ，＝C［i］，否则＝min｛A，C［i］｝，其中［r］表示工件排在第r个位置。

证明 过程完全类似于王吉波等［19］，Seidmann等［30］，故省略。

证明1）对于情况β≥γ，由定理1可知，对于任意给定排序，每个工件的工期应等于它们各自的完工时间，所以没有工件会提前完工和发生延迟，即Ej＝0，Tj＝0，j＝1，2，…，n，因此

因此目标函数为最小化γ∑max（0，Cj－A），或最小化∑max（0，Cj－A）（因γ为常数）。通常公共工期的最大延迟问题的模型为：∑max（0，Cj－d），如果其中的公共工期d被替换成本文中的A，则变成∑max（0，Cj－A），也就是笔者要求的最优目标函数，故由引理4，最优排序能通过把工件按照aj的非减顺序排列得到（SPT规则）。

2）对于情况β＜γ。

因为dj＝min（A，Cj）（根据定理1），可以得出dj≤A和Aj＝0。此时提前完工时间为零，即Ej＝0。

在排序π中，工件i和工件j为2个连续加工的工件，并假设ai＞aj且工件i和工件j分别位于第［i］和第［i＋1］个位置，π1和π2分别为第［i］个位置之前的工件的加工顺序和第［i＋1］个位置之后的工件的加工顺序，故排序为（π1，Ji，Jj，π2），现利用相邻交换法来证明结论。

图1描述了位置［i］和［i＋1］上的工件的完工时间和期望工期A之间的关系。见图1a，可知

然后交换第［i］和第［i＋1］个位置上的工件，其他不变，故排序变为（π1，Jj，Ji，π2），则

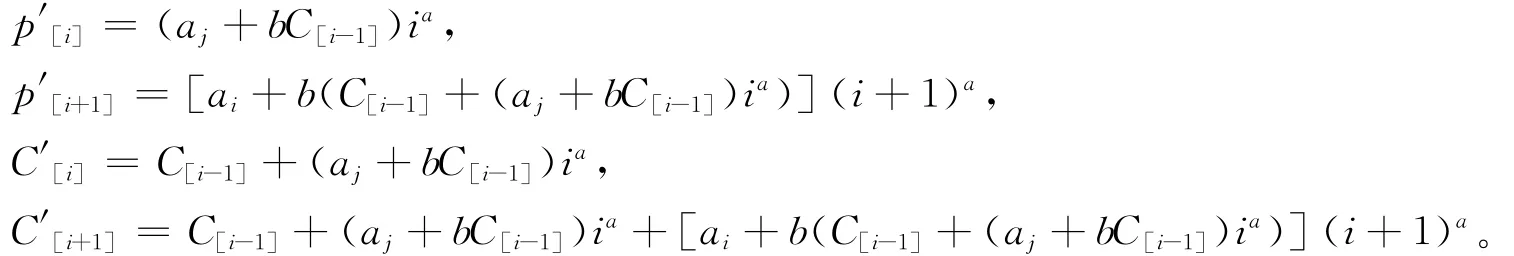
因为ai＞aj，所以

1）因为交换后不影响π1中的工件，所以目标函数的提前成本和延迟成本为零，而机会成本则没有发生变化，因此，总成本不变。

2）下面，来讨论一下交换工件Ji和Jj后对总成本的影响。

ⅰ）当C′［i］≤A时，对于工件Ji来说，交换前Ji的惩罚成本为β（C［i］－A），交换后的惩罚成本为β（－A）；对于工件Jj来说，交换前Jj的惩罚成本为β（C［i＋1］－A），交换后的惩罚成本为零，所以交换后对总成本的影响将会变小。

ⅱ）当C′［i］＞A时，对于工件Ji来说，交换前Ji的惩罚成本为β（C［i］－A），交换后的惩罚成本为β（C′［i＋1］－A）；对于工件Jj来说，交换前Jj的惩罚成本为β（C［i＋1］－A），交换后的惩罚成本为β（C′［i］－A）或为零，所以交换后对总成本的影响将会变小。

3）虽然交换后不影响π2中的工件，但交换后C［i＋1］＞C′［i＋1］，使得π2中工件的实际加工时间缩短，因此，总成本将会变小。

图1 A的不同位置情况

算法1

第1步 把工件按照SPT规则进行排序，即按照a［1］≤a［2］≤…≤a［n］进行排序。

第2步 比较β，γ的大小关系，如果β≥γ，＝C［i］，否则＝min｛A，C［i］｝。

例1 考虑6个工件J＝｛J1，J2，J3，J4，J5，J6｝的排序问题，其中a1＝10，a2＝8，a3＝7，a4＝15，a5＝14，a6＝3，α＝15，β＝20，γ＝5，b＝0.05，a＝－0.322，A＝30。

解 第1步 由于a6≤a3≤a2≤a1≤a5≤a4，因此最优排序为（J6，J3，J2，J1，J5，J4）；

第2步 因β≥γ，d6＝C6＝3，d3＝C3＝3＋（7＋0.05×3）×2－0.322＝8.719 7，

下面给出王吉波等［19］类似的算例来说明算法1是如何求解问题

例2 考虑6个工件J＝（J1，J2，J3，J4，J5，J6）的排序问题，其中a1＝10，a2＝8，a3＝7，a4＝15，a5＝14，a6＝3，α＝15，β＝20，γ＝25，b＝0.05，a＝－0.322，A＝30。

解 第1步 由于a6≤a3≤a2≤a1≤a5≤a4，因此最优排序为｛J6，J3，J2，J1，J5，J4｝；

第2步 因β＜γ，根据例1和算法1得

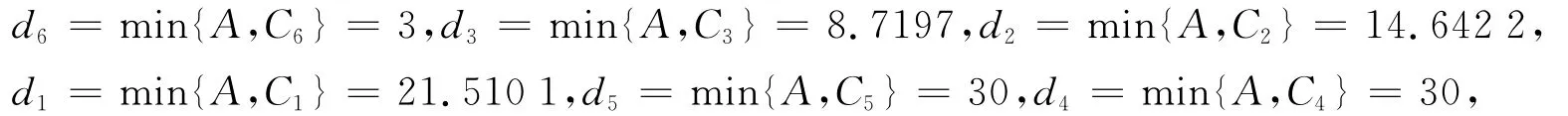
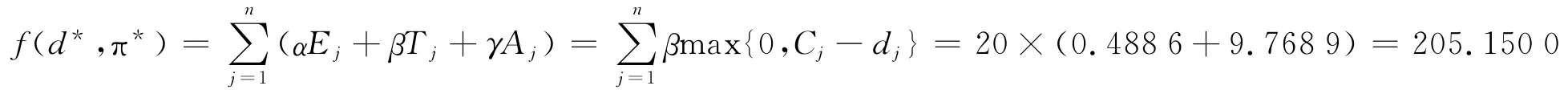
3 结论与展望

本文研究了工件同时具有学习和恶化效应的不同工期指派排序问题，其中机器限定为1台，目标函数为最小化提前成本、延迟成本和交货期成本的加权和。证明了该问题是多项式可解的并给出了最优算法。对于工件同时具有学习效应和恶化效应的排序问题，还有许多研究工作可做，比如研究多机（平行机或流水作业）问题，研究工期给定的排序问题，或者研究一般的恶化函数和学习效应函数等，探讨这些问题的可解情况以及对于NP－难的问题建立有效的近似算法和设计其他更好更快的算法是进一步研究中有意义的工作。

［1］BADIRU A B.Computational survey of univariate and multivariate learning curve models［J］.IEEE Trans Eng Manage，1992，39（2）：176－188.

［2］GUPTA J N D，GUPTA S K.Single facility scheduling with nonlinear processing times［J］.Comput Ind Eng，1988，14（4）：387－393.

［3］BROWNE S，YECHIALI U.Scheduling deteriorating jobs on a single processor［J］.Oper Res，1990，38（3）：495－498.

［4］BISKUP D.Single－machine scheduling with learning considerations［J］.Eur J Oper Res，1999，115（1）：173－178.

［5］CHENG T C E，Wang Guoqing.Single machine scheduling with learning effect considerations［J］.Ann Oper Res，2000，98（1／2／3／4）：273－290.

［6］孙林辉，王丹，王吉波.具有学习效应的总完工时间流水作业问题［J］.系统管理学报，2011，20（1）：114－118.

［7］MOSHEIOV G.Scheduling problems with a learning effect［J］.Eur J Oper Res，2001，132（3）：687－693.

［8］BISKUP D.A state－of－the－art review on scheduling with learning effects［J］.Eur J Oper Res，2008，188（2）：315－329.

［9］RUDEK R.Computational complexity and solution algorithms for flowshop scheduling problems with the learning effect［J］.Comput Ind Eng，2011，61（1）：20－31.

［10］王吉波，刘璐.带准备时间的任务单机学习效应排序问题［J］.大连理工大学学报，2013，53（6）：930－936.

［11］WANG Jibo，WANG Mingzheng.Worst－case analysis for flow shop scheduling problems with an exponential learning effect［J］.J Oper Res Soc，2012，63（1）：130－137.

［12］WANG Xiaoyuan，ZHOU Zhili，ZHANG Xi，et al.Several flow shop scheduling problems with truncated positionbased learning effect［J］.Comput Oper Res，2013，40（12）：2906－2929.

［13］LI Gang，WANG Xiaoyuan，WANG Jibo，et al.Worst case analysis of flow shop scheduling problems with a timedependent learning effect［J］.Int J Prod Econ，2013，142（1）：98－104.

［14］LEE Wenchiung，CHUNG Yuhsiang.Permutation flowshop scheduling to minimize the total tardiness with learning effects［J］.Int J Prod Econ，2013，141（1）：327－334.

［15］GAWIEJNOWICZ S.Time－dependent scheduling［M］.Berlin：Springer，2008.

［16］WANG Jibo，WANG Jianjun，JI Ping.Scheduling jobs with chain precedence constraints and deteriorating jobs［J］.J Oper Res Soc，2011，62（9）：1765－1770.

［17］王吉波，王建军，何平.具有共同松弛时间的恶化型工件排序问题研究［J］.大连理工大学学报，2012，52（6）：932－936.

［18］WANG Jibo，WANG Mingzheng.Minimizing makespan in three－machine flow shops with deteriorating jobs［J］.Comput Oper Res，2013，40（2）：547－557.

［19］王吉波，刘璐，许扬韬，等.具有恶化工件的不同工期指派问题研究［J］.沈阳航空航天大学学报，2013，30（5）：81－87.

［20］LEE Wenchiung.A note on deteriorating jobs and learning in single－machine scheduling problems［J］.Int J Business Econ，2004，3（1）：83－89.

［21］WANG Jibo.A note on scheduling problems with learning effect and deteriorating jobs［J］.Int J Syst Sci，2006，37（12）：827－833.

［22］WANG Jibo.Single－machine scheduling problems with the effects of learning and deterioration［J］.Omega，2007，35（4）：397－402.

［23］WANG Jibo，CHENG T C Edwin.Scheduling problems with the effects of deterioration and learning［J］.Asia Pac J Oper Res，2007，24（2）：245－261.

［24］WANG Jibo.Single machine scheduling with a time－dependent learning effect and deteriorating jobs［J］.J Oper Res Soc，2009，60（4）：583－586.

［25］WANG Jibo，HUANG Xue，WANG Xiaoyuan，et al.Learning effect and deteriorating jobs in the single machine scheduling problems［J］.Appl Math Model，2009，33（10）：3848－3853.

［26］WANG Jibo，GUO Qian.A due－date assignment problem with learning effect and deteriorating jobs［J］.Appl Math Model，2010，34（2）：309－313.

［27］WANG Jibo，WANG Cheng.Single－machine due－window assignment problem with learning effect and deteriorating jobs［J］.Appl Math Model，2011，35（8）：4017－4022.

［28］WANG Jibo，WANG Mingzheng，JI Ping.Single machine total completion time minimization scheduling with a timedependent learning effect and deteriorating jobs［J］.Int J Syst Sci，2012，43（5）：861－868.

［29］LOW Chinyao，LIN Wenyi.Some scheduling problems with time－dependent learning effect and deteriorating jobs［J］.Appl Math Model，2013，37（20）：8865－8875.

［30］SEIDMANN A，PANWALKAR S S，Smith M L.Optimal assignment of due－dates for a single processor scheduling problem［J］.Int J Prod Res，1981，19（4）：393－399.