量子粒子群结合小波变换识别结构模态参数
2014-05-16巩文龙
常 军,巩文龙
(苏州科技学院土木工程学院,江苏 苏州 215011)
量子粒子群结合小波变换识别结构模态参数
常 军,巩文龙
(苏州科技学院土木工程学院,江苏 苏州 215011)
通过对结构响应进行连续小波变换将多自由度模态参数识别转化为多个单自由度模态参数识别。建立小波骨架理论公式与由结构输出信号计算而得的小波骨架之差为目标函数的优化问题,通过搜索包含于小波骨架理论公式中的模态参数的取值而使目标值最小,从而将优化问题转化为模态参数识别问题。量子粒子群算法是一种基于群体智能理论的优化算法。将量子粒子群算法应用到上述方法中一次性识别出结构的频率、阻尼和振型。最后采用数值模拟的简支梁对该方法进行有效性验证。结果表明,量子粒子群算法结合连续小波变换可以有效地识别环境激励下的结构模态参数。
连续小波变换;量子粒子群算法;环境激励;结构模态参数识别;智能优化算法
以结构动力学为基础的传统结构模态参数识别方法是以结构的输入和输出信号为基础的。而在实际工程中,由于结构尺寸大导致人工激励困难且价格昂贵,从而限制了其应用。研究表明以大地脉动及其他环境因素共同对结构产生的环境激励基本满足白噪声的特性,这使得基于环境激励的结构模态参数识别成为了可能。环境激励方法因其无需激励设备、不影响结构正常使用、试验简便、所需人力少、不受结构形态和大小的限制、实验费用低、不会对结构产生局部损伤等优点,而备受业内人士青睐。近年来,环境激励方法的发展已有长足的进展,比较成熟的方法有频域法、时域法和时频域法三种。其中频域法有峰值法、频域分解法、最小二乘复频域法等;时域法有,时间序列分析方法、随机减量法、ITD方法和自然激励法、随机子空间方法、最小二乘复指数法和特征系统实现法等。时频法有魏格纳分布和短时傅里叶变换、小波变换和Hilbert-Huang变换法等[1-2]。
量子粒子群算法(QPSO)是在粒子群(PSO)算法基础上发展起来的一种基于群体智能理论的优化算法,因其具有计算精确、所需参数少、编程简单、容易收敛且收敛速度快等优势而备受关注[3-8]。本文将QPSO算法与连续小波变换(CWT)相结合,简化小波变换识别步骤,提高识别精度。
1 连续小波变换(CWT)
对任意函数f(t)∈L2(R)进行连续小波变换:
时域:
2 量子粒子群优化算法(QPSO)
QPSO克服了粒子群算法(PSO)的致命缺陷:容易陷入局部最优而无法得到全局最优结果[4-5]。

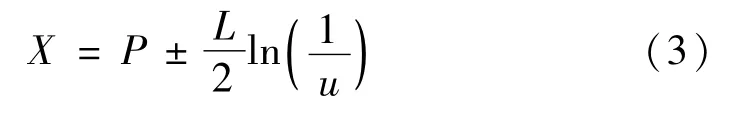
式中,u~U(0,1),L为δ势阱的特征长度,它随着时间变化。
粒子的更新方程为[4-5]

式中,m为粒子数,n为维数,φ~U(0,1),pij为由个体经验知识确定的最优值,Gj为由群体知识确定的群体最优值,α为收缩扩张系数,它是QPSO算法除群体规模和迭代次数以外的唯一控制参数,可按下式确定[4-5]:
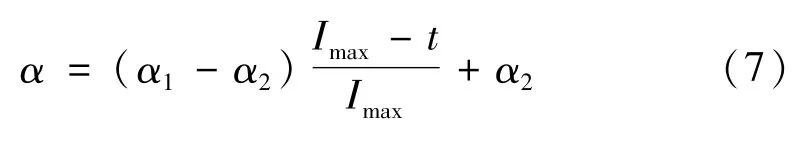
式中,α1,α2分别为α的初始值和终值,t为迭代次数。Imax为允许最大迭代次数。
3 QPSO+CWT识别结构模态参数
设y(t)为k自由度结构的响应信号,表示为:

式中,yi(t),Ai,ωni,ωdi,ζi,φi分别为第i阶(i=1,2,…,k)自由振动响应,幅值,无阻尼固有圆频率,有阻尼圆频率,阻尼比,相位角,且满足
将(8)式进行小波变换得:

式中j为复数的虚部单位
采用改进复Morlet小波函数,频域表达式为:

式中,ω0为小波中心频率,R为带宽参数。
小波基函数为:
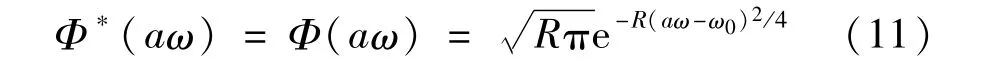
将式(11)代入式(9),整理得:

设ai为第i阶模态对应的尺度,由尺度与频率对应关系ai=ω0/ωdi得,当aωdi=ω0,即a=ai,ψ*(aωdi)取极大值,在(ai,b)处形成小波脊,整个时间区域形成小波脊线,在小波脊线处的小波系数构成小波骨架。换而言之,在第i个峰值处,第i阶模态的小波系数贡献最大,其他模态对应的小波系数幅值低贡献小,可以忽略不计[11],则多自由度系统的第模态小波系数为:

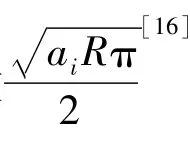
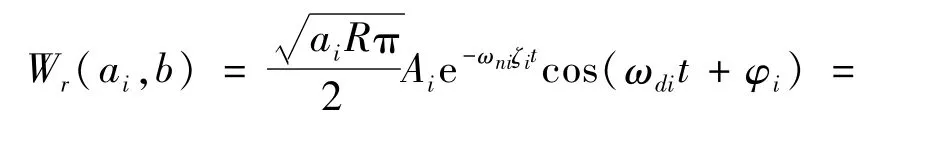

Wr(ai,b)为小波骨架Wf(ai,b)的实部,式(14)中包含第i阶Ai,ωni,ζi,φi四个未知参数,令Xi=(Ai,ωni,ζi,φi),Xi=(),将式(14)改写为:
min J(Xi)=g2(Xi)=[(ai,b)-Wr(ai,b)]2(15)式中,W′r(ai,b)为理论第i阶小波骨架实部,Wr(ai,b)为实测信号的小波骨架实部。
以式(15)作为QPSO算法的目标函数,Xi作为优化变量,优化第i阶模态参数,这样就将模态参数识别问题就转化为非线性优化问题。在该过程中,结构的第i阶模态参数(包括频率、阻尼比和振型)可以一次性识别出,从而将小波变换中频率、阻尼和振型要分别识别的过程进行了简化。其中各参数满足以下约束条件:
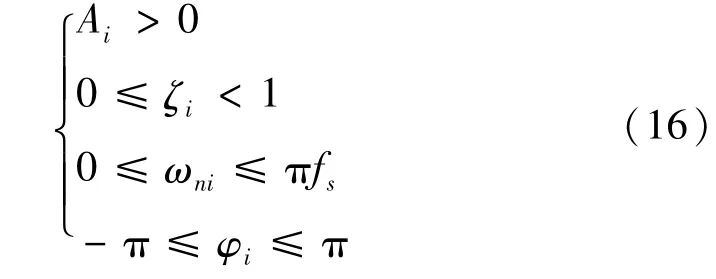
式中,fs为信号的采样频率。
4 实例分析
建立长10 m,宽200 mm,高250 mm的等截面混凝土简支梁数值模型,材料弹性模量为2.8E04 MPa,密度为2 500 kg/m3,如图1所示。按瑞利阻尼设置阻尼比,其中第一阶和第六阶设置为1.0%,其余按照公式计算而得。

图1 简支梁模型Fig.1 Simple support beam model
将简支梁均匀划分为20等份,每份长0.5 m,除两端支座处,共19个节点,在每个节点处施加由Matlab程序产生的不同的白噪声模拟环境激励。并在梁上19个节点处采集加速度,采样频率为200 Hz,采样时长5分钟。进而计算不同点采集加速度的互功率谱。分别采用QPSO+CWT算法、传统的CWT算法和峰值法进行结构模态参数识别。在识别过程中QPSO算法的粒子数目取100,迭代次数为10 000次,复Morlet小波里ω0取3,取20,识别结果如表1所示。为了研究该方法的抗噪性,对输出信号识别结果分别加入5%、10%、20%和30%的噪声(噪声最大幅值与响应信号最大幅值之比),采用文中所述方法进行识别,结果见表2。QPSO+CWT算法识别的前六阶振型如图2~图7所示。
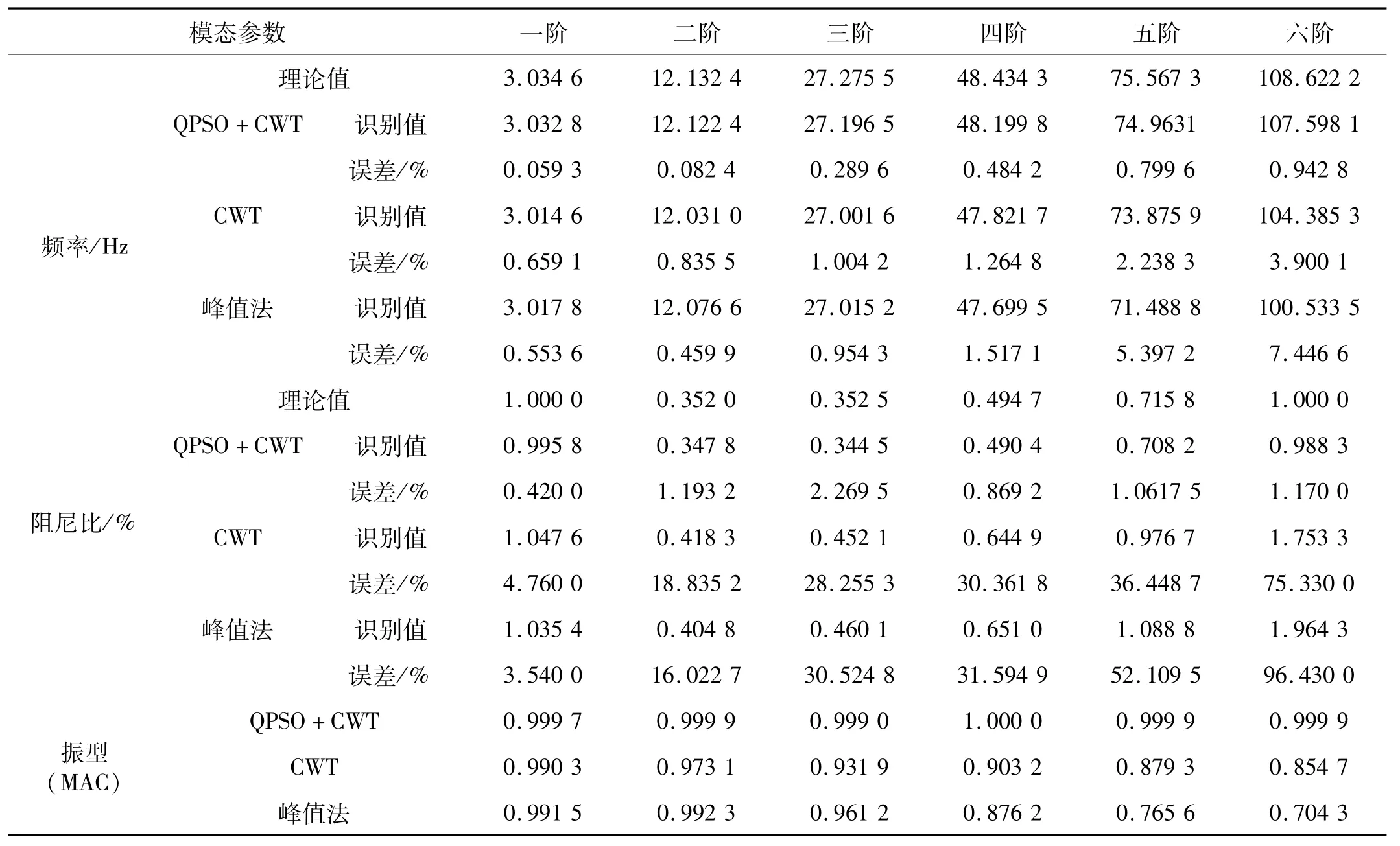
表1 采用不同方法得到的计算结果Tab.1 Identification results obtained by different methods

表2 采用QPSO+CWT算法识别的不同噪声水平下的计算结果Tab.2 Identification results of different noise level by QPSO+CWT
表中MAC为模态判定准则[13]:

式中:φ1、φ2分别为两不同向量,若MAC接近于1,则向量相同,若接近于0,则不同。
由表1及图2-6的识别结果可以清楚地看出:论文的QPSO+CWT算法能够比较精确地识别出模态参数,且比传统CWT算法和峰值法的精度要高。根据表2的识别结果可以发现,QPSO+CWT具有很强的抗噪性。究其原因是该算法过程中的互相关计算过程中剔除了信号中的噪声影响,进而提高了抗噪性。这与文献[13]的结论完全相同。

图3 第二阶模态振型Fig.3 The 2nd modal shape
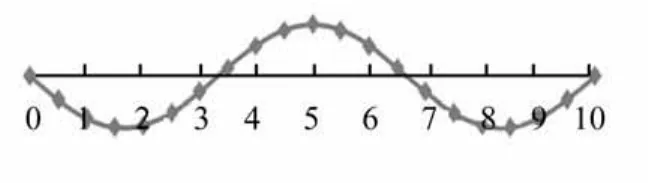
图4 第三阶模态振型Fig.4 The 3rd modal shape

图5 第四阶模态振型Fig.5 The 4th modal shape

图6 第五阶模态振型Fig.6 The 5th modal shape

图7 第六阶模态振型Fig.7 The 6th modal shape
5 结 论
采用CWT将结构的多自由度模态参数识别转化为多个单自由度模态参数识别,进而采用QPSO算法将模态参数识别问题转化为优化问题。通过实例研究得出以下结论:
(1)QPSO+CWT算法能够有效地识别出结构模态参数,且识别精度比传统的CWT算法和峰值法要高得多;
(2)QPSO+CWT算法具有较强的抗噪性,究其原因是文中所述方法中的互相关函数的计算过程剔除了白噪声的影响,这与文献[13]的结论是一致的;
(3)QPSO+CWT法在识别模态时,使用改进复Morlet小波,和的增大提高频域分辨率的同时,时域分辨率降低,导致阻尼识别效果差,要得到更好识别结果还有待进一步研究。QPSO+CWT算法必将对结构健康监测和结构状态评估的发展起到一定的促进作用。
[1]Doebling SW,FarrarCR,PrimeMB.Damage identificationandhealthmonitoringofstructuraland mechanicalsystemfromchangesintheirvibration characteristics:A literature review[R].Los Alamos:Los Alamos National Laboratory,1996.
[2]沈方伟,杜成斌.环境激励下结构模态参数识别方法综述[J].电子测试,2013,5:179-181.
SHEN Fang-wei,DU Cheng-bin.An overview of modal identification from ambient responses[J].Electronic Test,2013,5:179-181.
[3]Sun Jun,Xu Wenbo,Feng Bin.Adaptive parameter control forquantum-behavedparticleswarmoptimizationon individual level[C].Proceedings of IEEE international conference on system,2005:3049-3054.
[4]Sun J,Xu W,Fang W.Quantum-behaved particle swarm optimization with a hybrid probability distribution[C].In:PRICAI 2006:TRENDS IN Artificial Intelligence,2006,737 -746.
[5]黄宇,韩璞,刘长良,等.改进量子粒子群算法及其在系统辨识中的应用[J].中国电机工程学报,2011,31(20):114-122.
HUANG Yu,HAN Pu,LIU Chang-liang,et al.An improved quantum particle swarm optimization and its application in system identification[J].Proceedings of the CSEE,2011,31 (20):114-122.
[6]沈佳宁,孙俊,须文波.运用QPSO算法进行系统辨别的研究[J].计算机工程与应用,2009,45(9):67-70.
SHEN Jia-ning,SUN Jun,XU Wen-bo.System identification based on QPSO algorithm[J].Computer Engineering and Application,2009,45(9):67-70.
[7]胡峰,吴波,胡友民,等.利用粒子群优化算法实现阻尼比和频率的精确识别[J].振动与冲击,2009,28(7):8-11.
HU Feng,WU Bo,HU You-min,et al.Exact evaluation of damping frequency based on particle optimization algorithm [J].Journal of Vibration and Shock,2009,28(7):8-11.
[8]王峰,邢科义,徐小平.系统辨识的粒子群优化算法[J].西安交通大学学报,2009(2):116-120.
WANGFeng,XINGKe-yi,XUXiao-ping.Asystem identification method using particle swarm optimization[J].Journal of Xi'an Jiaotong University,2009(2):116-120.
[9]许东杰,贾春玉,崔艳超等.基于量子粒子群算法的BP网络板型模式识别研究[J].燕山大学学报,2011,35(1):35-39.
XU Dong-jie,JIA Chun-yu,CUI Yan-chao,et al.Study on BP network flatness pattern recognition based on quantum particle swarm optimization algorithm[J].Journal of Yanshan University,2011,35(1):35-39.
[10]徐小平,钱富才,刘丁,等.基于PSO算法的系统辨识方法[J],系统仿真学报,2008(13):3525-3528.
XU Xiao-ping,QIAN Fu-cai,LIU Ding,et al.Method of system identification based on PSO algorithm[J].Journal of System Simulation,2008(13):3525-3528.
[11]许少华,王浩,王颖,等.一种改进的量子粒子群优化算法及其应用[J].计算机工程与应用,2011,47(20):34-37.
XU Shao-hua,WANG Hao,WANG Ying,et al.Improved quantumparticleswarmoptimizationalgorithmandits application[J].Computer Engineering and Applications,2011,47(20):34-37.
[12]常军,张启伟,孙利民.稳定图方法在随机子空间识别模态参数中的应用[J].工程力学,2007,24(2):39-44.
CHANG Jun,ZHANG Qi-wei,SUN Li-min.Application of stabilization diagram to modal parameter identification by stochastic subspace method[J].Engineering Mechanics,2007,24(2):39-44.
[13]申凡,郑敏,鲍明.用互功率谱进行未知激励下的模态振型识别[J].南京理工大学学报,2000,24(2):117-120.
SHEN Fan,ZHENG Min,BAO Ming.Identification of mode shape by fitting cross-power spectra under unknown excitation [J].JournalofNanjingUniversityofScienceand Technology,2000,24(2):117-120.
[14]Lardies J,Ta M N,Berthillier M.Modal parameter estimation based on the wavelet transform of output data[J].Archive of Applied Mechanics,2004,73(9-10):718-733.
[15]罗光坤,张令弥.Morlet小波用于环境激励下的模态参数识别研究[J].地震工程与工程振动,2007,27(4):109 -115.
LUO Guang-kun,ZHANG Ling-mi.Study on identification of modal parameters under ambient excitation based on morlet wavelet[J].JournalofEarthquakeEngineeringand Engineering Vibration,2007,27(4):109-115.
[16]伊廷华,李宏男,王国新.基于小波变换的结构模态参数识别[J].振动工程学报,2006,19(1):51-56.
YI Ting-hua,LI Hong-nan,WANG Guo-xin.Structural modal parameter identification based on wavelet transform [J].Journal of Vibration Engineering,2006,19(1):51 -56.
Structural modal parameter identification based on quantum-behaved particle swarm optimization combined with wavelet transformation
CHANG Jun,GONG Wen-long
(School of Civil Engineering,University College of Science and Technology of Suzhou,Suzhou 215011,China)
Multi-DOF structural modal parameter identification was converted into several single-DOF structural modal parameter identifications by treating structural output data with continuous wavelet transformation.An optimization with an objective function of the difference between theoretical formula of wavelet skeleton and the wavelet skeleton calculated from structural output data was performed.The minimum objective value was gained through searching reasonable modal parameters included in the theoretical formula of wavelet skeleton.And the optimization was turned into structural modal parameter identification.Quantum-behaved particle swarm optimization,as a swarm intelligence optimization algorithm,was used in the structural modal parameter identification above to identify the structural modal parameters(frequencies,damp ratios and modal shapes)simulataneously under ambient excitation.Finally,the modal parameter identification method based on quantum-behaved particle swarm optimization combined with continuous wavelet transformation presented herein was verified with a numerical simulation of a simply-supported beam.The results showed that the methodology herein can effectively be used to identify structural modal parameters under ambient excitation.
continuous wavelet transformation;quantum-behaved particle swarm optimization;ambient excitation;structural modal parameter identification;intelligence optimization algorithm
U441
A
10.13465/j.cnki.jvs.2014.23.008
国家科技支撑计划课题(2012BAJ11B01);江苏省自然科学基金项目(BK20141180);苏州科技学院科研基金项目(XKZ201304)
2014-04-01 修改稿收到日期:2014-07-28
常军男,博士,副教授,1973年生
