考虑两类赔款数据相关性的随机性准备金进展法及改进

段白鸽，张连增

（1.复旦大学经济学院，上海 200433；2.南开大学经济学院，天津 300071）

这里，对于

，有

（9）对于i≥2，j≥1，i+j≥n+1，从均值为

考虑两类赔款数据相关性的随机性准备金进展法及改进

段白鸽1，张连增2

（1.复旦大学经济学院，上海 200433；2.南开大学经济学院，天津 300071）

本文创新性地提出基于成对抽数的非参数Bootstrap方法、二元正态分布和Copulas函数三种考虑已决赔款与已报案赔款相关性的随机性准备金进展法，并结合非寿险精算实务中的经典流量三角形数据，应用R软件对三种考虑相关性的随机性准备金进展法进行了完整的编程实现，并模拟得到了最终损失、未决赔款准备金和IBNR的完整的预测分布。本文提出的考虑相关性的随机性准备金进展法不但考虑了两类赔款数据之间的相关性，而且体现了不同事故年已发生已报案未决赔款准备金进展情况之间的差异。这种处理相关性的思路和方法在多元准备金评估中具有重要的应用价值。

随机性准备金进展法；多元准备金评估；Copulas函数；Bootstrap方法；二元正态分布；预测分布

1 引言

准备金评估作为国际精算理论研究的前沿与热点，近30年来涌现出大量关于一元准备金评估随机性模型与方法的研究文献。经典文献可以参考England和Verrall［1-3］，England［4］，Clark［5］，Meyers［6］，Guszcza［7］，Wüthrich和Merz［8］，Peters等［9］，Björkwall等［10］，England等［11］。其中，England、Verrall和Wüthrich三位学者在这一领域作出了突出贡献。特别指出的是，2008年，Wüthrich和Merz［8］出版了国际上第一部系统介绍准备金评估随机性方法的划时代著作，该著作针对一些常见的准备金评估方法，详细推导了各种方法中准备金的均值估计和预测均方误差（Mean Square Error of Prediction，MSEP）估计的解析形式，并附有大量的数值实例。同年，张连增［12］出版了国内第一本系统介绍准备金评估随机性方法的专著。这两部著作几乎仍停留在准备金估计的MSEP的波动性度量上，鲜少涉及预测分布的模拟。而预测分布包含了更完整的分布信息，可以合理度量风险边际及任意感兴趣的风险测度，这方面最新著作见张连增和段白鸽［］。

伴随着一元准备金评估方法理论研究的成熟和实务中精算技术的进步，该领域的最新发展趋势就是多元随机性准备金评估方法的研究，即考虑多个存在相依结构的流量三角形的准备金评估问题。在聚合数据结构下，同时研究多个流量三角形的主要优势在于，研究多个流量三角形之间的相依性产生的多元化效应对准备金的均值估计和波动性度量（MSEP、预测分布）具有重要意义。在多元框架下，评估方法又可以进一步细分为基于不同类型赔款数据（如已决赔款与已报案赔款）相关性的多元准备金评估和基于不同业务线相依性的多元准备金评估两类。其中，研究基于已决赔款与已报案赔款相关性的多元准备金评估方法的意义在于，一方面，在实务操作中，基于两类赔款数据估计的未决赔款准备金往往存在显著差异，导致精算师对于两类赔款数据的选择产生困惑。另一方面，由于已决赔款包含于已报案赔款中，而已报案赔款又包含了额外的信息，这将影响未来的已决赔款，故这两类赔款数据本身存在相关性。然而，一元准备金评估方法却无法考虑这种相关性。这方面较新文献可以参考Liu Huijuan和Verrall［14］，Happ等［15］，Happ和Wüthrich［16］，张连增和段白鸽［17-19］。研究基于不同业务线相依性的多元准备金评估方法的意义在于，这种多元评估方法可以同时解决相依性问题和可加性问题。这方面最新进展见Zhang Yanwei等［20］，Merz等［21］。

结合这些研究，本文进一步扩展探讨考虑已决赔款与已报案赔款相关性的多元准备金评估方法，提出基于成对抽数的非参数Bootstrap方法、二元正态分布和Copulas函数三种考虑两类赔款数据相关性的随机性准备金进展法，并结合非寿险精算实务中的经典流量三角形数据，应用R软件对三种考虑相关性的随机性准备金进展法进行了完整的编程实现，并模拟得到了最终损失（UL）、未决赔款准备金（R）和已发生未报案未决赔款准备金（IBNR）的完整的预测分布。相比以往研究，本文的一个重要创新在于将基于Copulas函数度量变量间相依风险建模方法引入到考虑已决赔款与已报案赔款相关性的随机性准备金进展法中，为多元准备金评估方法的研究提供了新的分析思路，扩展了张连增和段白鸽［19］的研究成果。这些探索研究对精算学中定量风险管理技术的发展具有重要推动作用。

2 三种考虑两类赔款数据相关性的随机性准备金进展法

2.1 基于二元正态分布考虑两类赔款数据的相关性

令Pi，j和Ii，j（1≤i≤I，1≤j≤J）分别表示事故年i、进展年j的累计已决赔款和累计已报案赔款，和（1≤i≤I，1≤j≤J）分别表示事故年i、进展年j的增量已决赔款和增量已报案赔款，且不失一般性，假设I=J=n。则事故年i、进展年j的已发生已报案未决赔款准备金可以表示为Ri，j= Ii，j-Pi，j（1≤i，j≤n）。

在基于二元正态分布考虑两类赔款数据相关性的随机性准备金进展法中，模拟预测分布的具体步骤可以概括为：

（1）将流量三角形上三角累计已决赔款Pi，j和累计已报案赔款Ii，j转化为增量已决赔款和增量已报案赔款（i≥1，j≥1，i+j≤n+1）。

（2）构造残差。这里对上三角增量数据以列为研究对象，求每列数据的样本均值和、样本标准差和，对每列数据标准化，得到构造的两类残差流量三角形分别为：

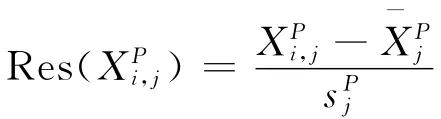
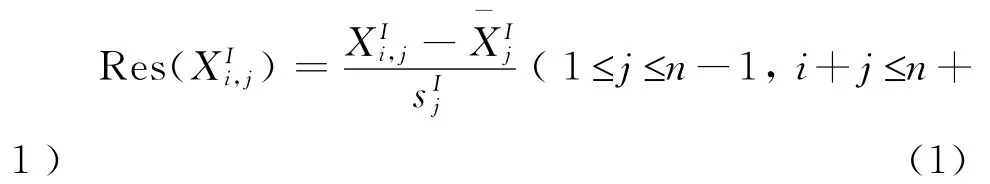
显然，这种构造残差的方式无法计算进展年n的残差，这里假设Res（XP1，n）=Res（XI1，n）=0。

（3）对两类残差进行调整［17-19］，构造调整后残差的二元正态分布。其中，相关系数的计算公式为：

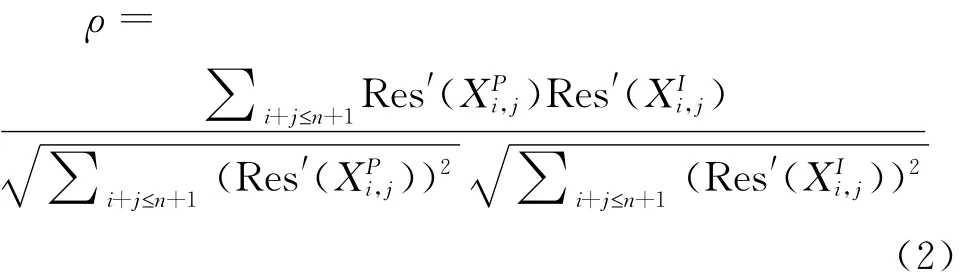
（4）从构造的二元正态分布中抽取调整后的残差样本Res*（）和Res*（），得到两类调整后残差流量三角形，其后按照式（1）进行反演变换，得到模拟的上三角增量赔款和、累计赔款和流量三角形，其计算公式为：

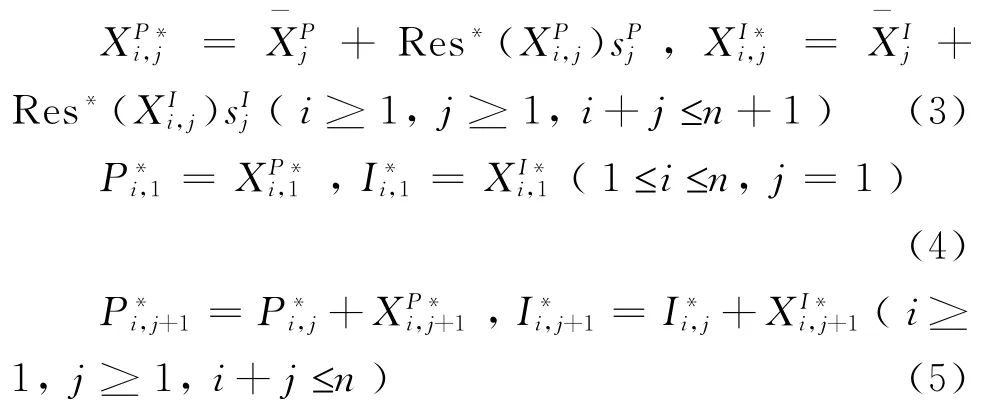
进而，定义如下事故年i、进展年j的（P/I）*比率为：

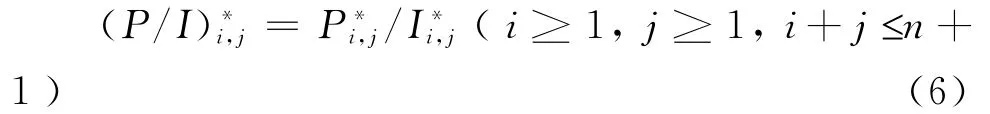
（5）在步骤（4）的基础上，计算模拟的上三角已发生已报案未决赔款准备金、准备金支付率、准备金结转率流量三角形，其计算公式为：（P/I）i*，j（i≥1，j≥1，i+j≤n）的一元线性回归模型：

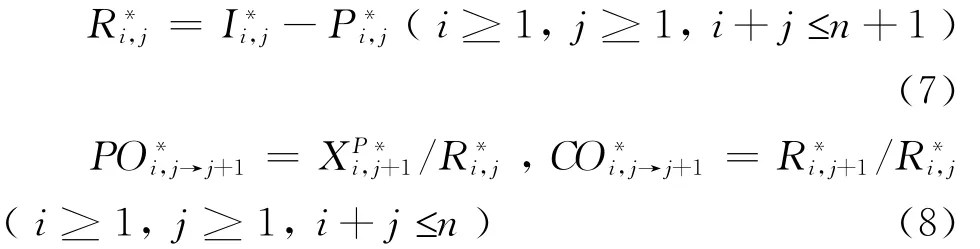
应用最小二乘法估计模型的回归系数，得到：

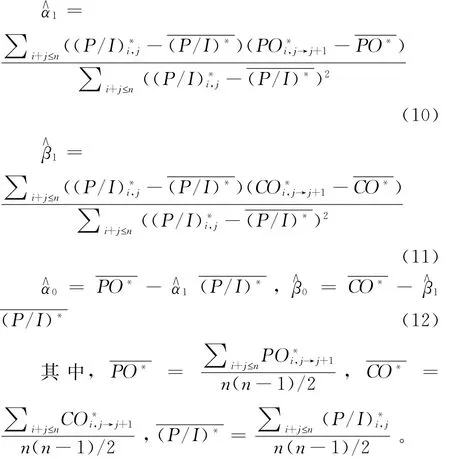
（7）对于事故年i，利用步骤（6）得到的模型参数估计值，首先估计：

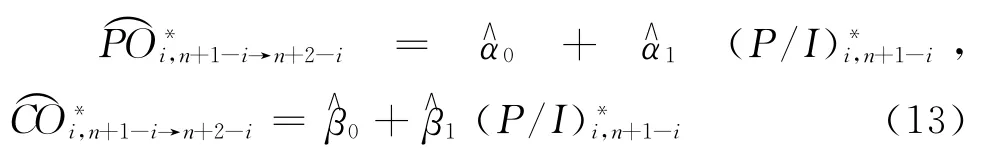
然后，对于i≥2，j≥1，i+j≥n+1，再按照准备金进展法的思路，逐步递归计算：

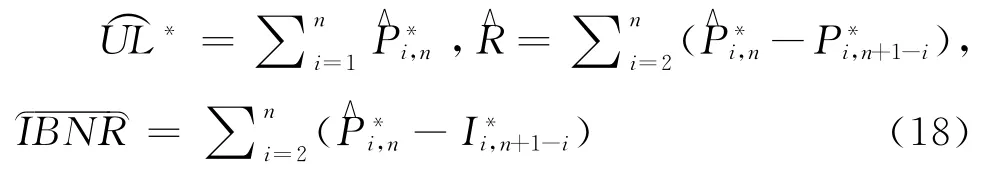
（8）计算模拟的上三角和下三角赔款数据中，进展年j（1≤j≤n-1）的支付率和结转率的均值、标准差，其计算公式为：、标准差为的正态分布中抽取支付率样本，得到模拟的单个支付率的下三角，从均值为、标准差为的正态分布中抽取结转率样本，得到模拟的单个结转率的下三角，进而按照步骤（7）的做法，便可实现UL、R和IBNR的预测分布的一次模拟。

这里，对于

，有

（9）对于i≥2，j≥1，i+j≥n+1，从均值为

（10）重复步骤（4）-（9），多次再抽样后，就可以得到UL、R和IBNR的预测分布，进而可以由该分布得到均值、标准差、分位数等相关的分布特征。

2.2 基于成对抽数的非参数Bootstrap方法考虑两类赔款数据的相关性

通常来说，上三角累计已决赔款Pi，j与累计已报案赔款Ii，j之间存在正的相关性。在模拟预测分布的过程中，为了描述这种相关性，一种更直观的处理方法就是将上三角每一事故年i、进展年j的两个调整后的残差Res*（）和Res*（）（i+j≤n+1）组成一对有序数组，在模拟预测分布的过程中，成对地抽取这两个调整后的残差样本。

2.3 基于Copulas函数考虑两类赔款数据的相关性

由于Copulas为多元分布建模提供了更一般的结构，且二元正态分布对应于一种特殊的Copula函数，为此，我们可以选取一些合适的Copulas函数来构造两类调整后的残差数据的二元分布。常见的描述二元分布的Copulas家族主要包括Clayton、Frank、Gumbel、Normal、Plackett等。由于不同Copulas家族建立的模型是非嵌套模型，故通常情况下，我们很难比较不同Copulas家族对应的模型的拟合效果。即便如此，为了选取一个合适的Copulas家族来为多元分布建模，我们仍可以计算各个模型估计中得到的一些统计量，如对数似然统计量（ln L）、赤池信息准则（AIC），以辅助选取更合适的模型。一般首选AIC统计量的值最小的模型，相应的AIC统计量的计算公式为：

其中，ln L表示对数似然函数的最大值，d表示自由度，n为每个维度的观测样本数。

3 模拟结果及分析

在模拟预测分布中，选取的累计已决赔款与累计已报案赔款数据来源于吴小平［22］，见附录中的表1和表2。

3.1 三种考虑相关性的随机性准备金进展法的数值结果及比较

按照本文第二部分的思路，下面详细给出了三种不同抽样方式下，考虑相关性的随机性准备金进展法模拟的预测分布及相关的分布特征，这里采用R软件对其进行算法实现。由于在应用R软件进行随机模拟时，可以设定不同的“种子”数。本文在各种抽样方式下，统一选取模拟次数为10000次，并选择了同一个“种子”数，这不但可以唯一确定模拟结果，而且有助于对各种抽样方法的结果进行比较。3.1.1 基于成对抽数和二元正态分布的模拟结果

图1和图2分别给出了基于成对抽数的非参数Bootstrap方法和二元正态分布两种不同抽样方式下，10000次模拟运算得到的UL、R和IBNR的模拟样本值。

从图1和图2可以看出，在应用成对抽数的非参数Bootstrap方法模拟UL、R和IBNR的预测分布时，出现了极小值-1.996e+27。在基于二元正态分布模拟UL、R和IBNR的预测分布时，出现了极大值4.485e+33。之所以会出现这些极大值或极小值，其原因在于当某次模拟得到的流量三角形中含有异常大或异常小的赔款额的情况下，可能导致无法满足相应的评估模型的假设条件，此时，直接模拟就会产生一些极端值。

在使用各种随机性准备金评估方法模拟预测分布的过程中，依赖于所选取的评估方法和抽样方式，不可避免地会产生一些极端值。从更一般意义上讲，这可以归结为准备金评估模型或方法的稳健性问题，这需要借鉴统计学中的各种模型诊断方法，并将其应用于具体的准备金评估模型中。目前在国际精算领域中，鲜少有这方面的研究文献。一种更直观的处理方法就是通过增加模拟次数，剔除模拟结果中的少量极端值，采用剔除极端值后的有效模拟结果来绘制各种预测分布。为此，我们引入“有效模拟次数”这一概念。有效模拟次数是指各种抽样方式下，绘制UL、R和IBNR的预测分布中选取的模拟样本个数。显然，相对于模拟次数来说，有效模拟次数应该足够大。从某种程度上讲，当模拟次数相同时，有效模拟次数越大，相应的评估方法越稳健。

图1 基于成对抽数非参数Bootstrap方法得到的UL、R和IBNR的模拟样本值

图2 基于二元正态分布得到的UL、R和IBNR的模拟样本值

图3 基于成对抽数和二元正态分布模拟得到的UL、R和IBNR的预测分布

我们剔除极端值之后，绘制了这两种不同抽样方式下，考虑相关性的随机性准备金进展法模拟的UL、R和IBNR的预测分布见图3，单位为千元，相应的分布特征如表4所示。

3.1.2 基于Copulas函数的模拟结果

（1）Copula函数的选取

经简单计算得出上三角两类调整后残差样本的相关系数为0.6687，这表明两类赔款数据之间存在很强的正相关关系。为了选取合适的Copula函数来描述这种正相关性，表3给出了采用半参数方法估计5种常用的Copulas函数，得到的相关性参数κ、相关系数τ和ρ的估计结果，以及ln L统计量和AIC统计量的值。从表3可以看出，5种Copulas函数中，Clayton Copula函数的AIC统计量的值最小。因此，我们建议首选Clayton Copula函数来描述两类调整后残差随机变量之间的相关性。

表3 不同Copulas函数的估计结果比较及检验统计量

（2）基于Clayton Copula函数模拟的预测分布图4给出了基于Clayton Copula函数的再抽样方式下，10000次模拟运算得到的UL、R和IBNR的模拟样本值。

从图4可以看出，基于Clayton Copula函数模拟预测分布时，模拟得到的UL、R和IBNR的极小值分别为327700、-100100和-228400。很明显可以看出，Clayton Copula函数的模拟结果更稳健。剔除极端值之后，图5绘制了基于Clayton Copula函数考虑相关性的随机性准备金进展法模拟得到的UL、R和IBNR的预测分布。为了便于与基于成对抽数和二元正态分布的模拟结果进行比较，图5中也给出了这两种抽样方式下模拟的预测分布，单位为千元，相应的分布特征如表4所示。

（3）其它三种Copulas函数模拟的预测分布

基于Frank、Gumbel、Plackett三种Copulas函数模拟UL、R和IBNR的预测分布时，都出现了极小值，其中，Frank Copula函数下的极小值为-3.051e+15，Gumbel Copula函数下的极小值为-1.826e+18，Plackett Copula函数下的极小值为-3.974e+16。显然，这三种Copulas函数都不如Clayton Copula函数的模拟结果稳健。为了与Clayton Copula函数的模拟结果进行比较，我们剔除极端值后，给出了这三种Copulas函数下，模拟得到的UL、R和IBNR的预测分布的分布特征，如表5所示。

图4 基于Clayton Copula函数得到的UL、R和IBNR的模拟样本值

图5 三种考虑相关性的随机性准备金进展法模拟得到的UL、R和IBNR的预测分布

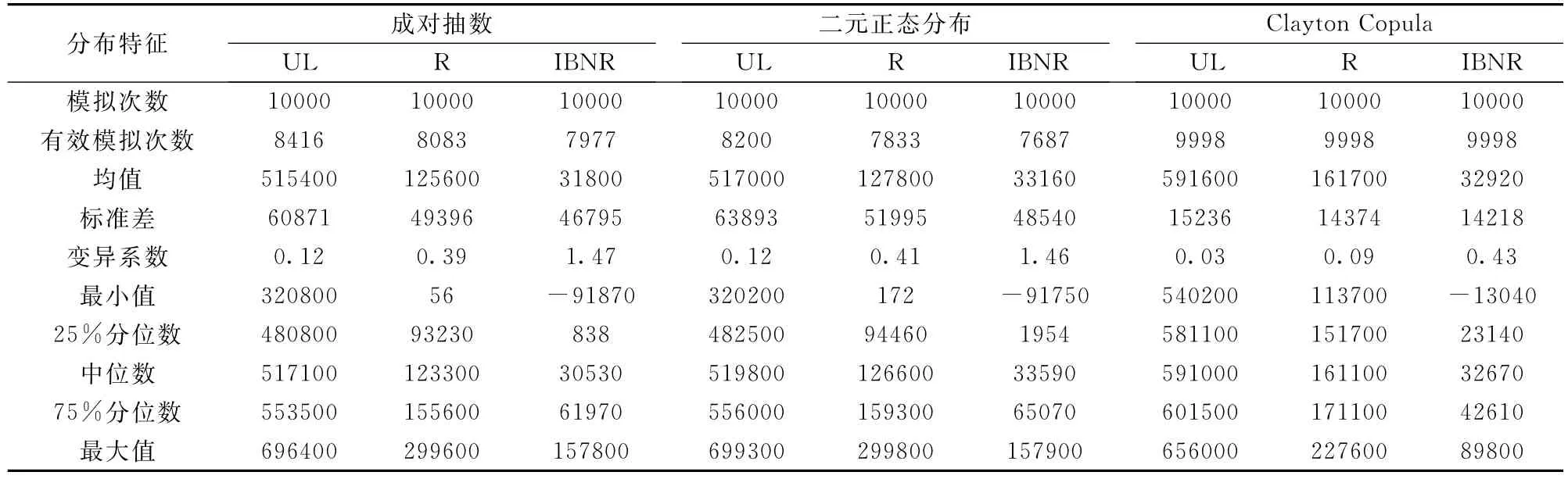
表4 三种考虑相关性的随机性准备金进展法得到的UL、R和IBNR的预测分布的分布特征

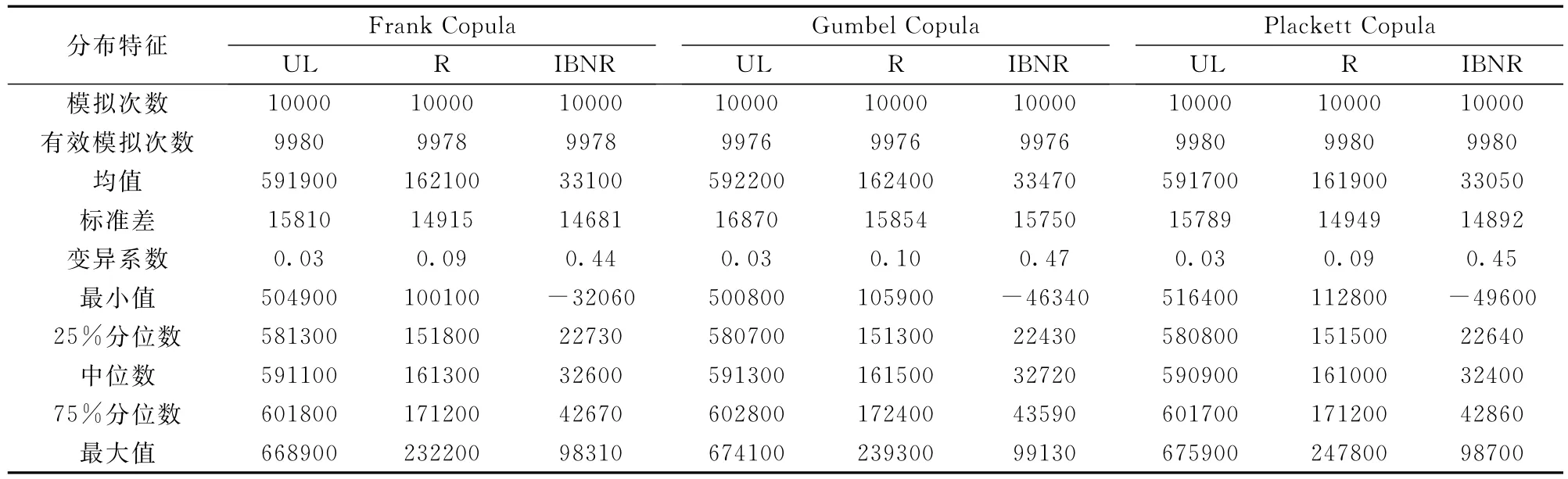
表5 基于其它三种Copulas函数模拟得到的UL、R和IBNR的预测分布的分布特征

3.2 主要结论

从上面的数值结果可以得出以下结论：

（1）从图3可以看出，剔除极端值后，基于成对抽数的非参数Bootstrap方法和基于二元正态分布模拟得到的预测分布几乎完全重合，表4中相应的分布特征也都很接近。这充分说明了非参数Bootstrap方法和基于二元正态分布的参数Bootstrap方法具有一致性。

（2）从图5可以看出，与Clayton Copula函数模拟的预测分布相比，基于成对抽数和二元正态分布模拟的UL和R的预测分布的均值明显更小一些，IBNR的预测分布的均值差异并不显著，UL、R和 IBNR的波动性明显大很多，这些特征也可以从表4中的均值、标准差、变异系数等相关的分布特征得到验证。针对这种差异，进一步探讨在一定的准则下，选取合理的相依建模方法是非常有必要的。

（3）从表4和表5可以看出，剔除极端值后，Clayton、Frank、Gumbel和Plackett四种Copulas函数下，考虑相关性的随机性准备金进展法模拟的预测分布的分布特征都很接近。

（4）在表4中，与成对抽数和二元正态分布两种抽样方式相比，当模拟次数为10000次时，基于Clayton Copula抽样方式下，UL、R和IBNR的预测分布的有效模拟次数都是9998次，表明基于Clayton Copula考虑相关性的随机性准备金进展法更稳健些，这也可以从图1、图2和图4的模拟样本值中得到验证。类似地，在表5中，三种Copulas函数的有效模拟次数都小于9998次，也一定程度上表明采用Clayton Copula函数来描述这两类调整后残差数据的相关性更合适。

4 结语

本文提出了基于成对抽数的非参数Bootstrap方法、二元正态分布和Copulas函数三种考虑已决赔款与已报案赔款相关性的随机性准备金进展法，并结合非寿险精算实务中的经典流量三角形数据，应用R软件对三种考虑相关性的随机性准备金进展法进行了完整的编程实现，并模拟得到了最终损失、未决赔款准备金和IBNR的完整的预测分布。本文提出的考虑相关性的随机性准备金进展法不但考虑了两类赔款数据之间的相关性，而且通过建立支付率与P/I比率、结转率与P/I比率的一元线性回归模型来体现不同事故年已发生已报案未决赔款准备金进展情况之间的差异。类似地，这种处理相关性的思路也适合于另一种基于不同类型赔款数据相关性的多元准备金评估，即考虑两类赔款数据相关性的随机性Munich链梯法。作为进一步的研究方向，可以将Copulas函数应用于另一类基于不同业务线的多元准备金评估中。

附录

表1 累计已决赔款数据 单位：千元

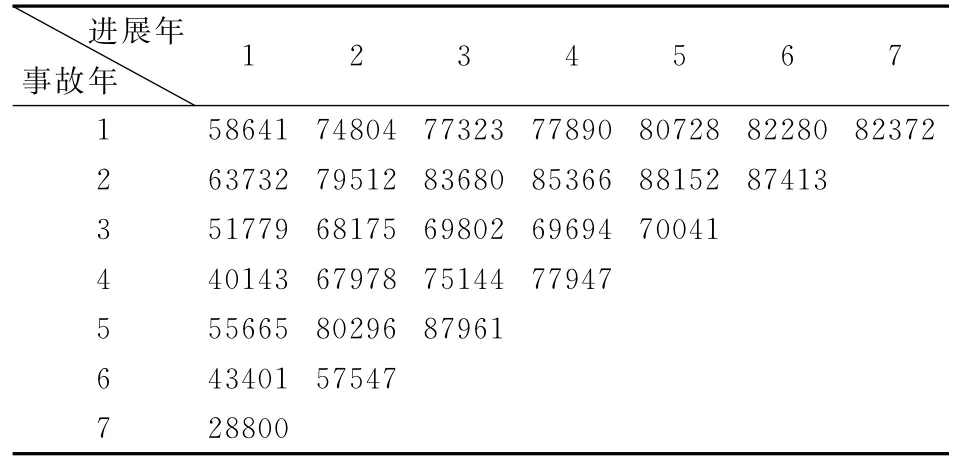
表2 累计已报案赔款数据 单位：千元

［1］England P D，Verrall R J.Analytic and bootstrap estimates of prediction errors in claims reserving［J］.Insurance：Mathematics and Economics，1999，25（3）：281-293.

［2］England P D，Verrall R J.Stochastic claims reserving in general insurance［J］.British Actuarial Journal，2002，8（3）：443-518.

［3］England P D，Verrall R J.Predictive distributions of outstanding liabilities general insurance［J］.Annuals of Actuarial Science，2007，1（2）：221-270.

［4］England P D.Addendum to“analytic and bootstrap estimates of prediction errors in claims reserving”［J］.Insurance：Mathematics and Economics，2002，31（3）：461-466.

［5］Clark D R.LDF curve fitting and stochastic loss reserving：a maximum likelihood approach［J］.Casualty Actuarial Society Forum，2003，（3）：41-91.

［6］Meyers G.Estimating predictive distributions for loss reserve models［J］.Variance，2007，1（2）：248-272.

［7］Guszcza J.Hierarchical growth curve models for loss reserving［J］.Casualty Actuarial Society E-Forum，2008，（3）：146-172.

［8］Wüthrich M V，Merz M.Stochastic Claims Reserving Methods in Insurance［M］.New York：Wiley，2008.

［9］Peters G W，Shevchenko P V，Wüthrich M V.Model uncertainty in claims reserving within Tweedie's compound Poisson models［J］.ASTIN Bulletin，2009，39（1）：1-33.

［10］Björkwall S，Hössjer O，Ohlsson E，et al.A generalized linear model with smoothing effects for claims reserving［J］.Insurance：Mathematics and Economics，2011，49（1）：27-37.

［11］England P D，Verrall R J，Wüthrich M V.Bayesian over-dispersed Poisson model and the Bornhuetter-Ferguson claims reserving method［J］.Annals of Actuarial Science，2012，6（2）：258-283.

［12］张连增.未决赔款准备金评估的随机性模型与方法［M］.北京：中国金融出版社，2008.

［13］张连增，段白鸽.非寿险索赔准备金评估随机性方法［M］.北京：北京大学出版社，2013.

［14］Liu Huijuan，Verrall R J.Bootstrap estimation of the predictive distributions of reserves using paid and incurred claims［J］.Variance，2010，4（2）：121-135.

［15］Happ S，Merz M，Wüthrich M V.Claims development result in the paid-incurred chain reserving method［J］. Insurance：Mathematics and Economics，2012，51（1）：66-72.

［16］Happ S，Wüthrich M V.Paid-incurred chain reserving method with dependence modeling［J］.ASTIN Bulletin，2013，43（1）：1-20.

［17］张连增，段白鸽.准备金评估的随机性Munich链梯法及改进——基于Bootstrap方法的实证分析［J］.数量经济技术经济研究，2011，28（11）：98-111.

［18］张连增，段白鸽.未决赔款准备金评估的随机性Munich链梯法［J］.数理统计与管理，2012，31（5）：880-897.

［19］张连增，段白鸽.基于已决赔款与已报案赔款相关性的随机性准备金进展法［J］.管理评论，2013，25（5）：155-166.

［20］Zhang Yanwei，Dukic V，Guszcza J.A Bayesian nonlinear model for forecasting insurance loss payments［J］.Journal of Royal Statistical Society，Series A，2012，175（2）：637-656.

［21］Merz M，Wüthrich M V，Hashorva E.Dependence modeling in multivariate claims run-off triangles［J］. Annals of Actuarial Science，2013，7（1）：3-25.

［22］吴小平.保险公司非寿险业务准备金评估实务指南［M］.北京：中国财政经济出版社，2005.

Stochastic Reserves Development Methods Based on the Correlation Among Paid-Incurred Payments Data and Their Improvement

DUAN Bai-ge1，ZHANG Lian-zeng2
（1.School of Economics，Fudan University，Shanghai 200433，China；2.School of Economics，Nankai University，Tianjin 300071，China）

Three stochastic reserves development methods are innovatively proposed in this paper considering the correlation between paid-incurred payments data，i.e.based on non-parametric Bootstrap method with pairwise resampling，based on bivariate normal distribution，and based on Copulas function.Combined the classic run-off triangles data in the non-life actuarial practice，a complete programming for three stochastic reserve development methods is provided based on the correlation with R software.Further，the complete predictive distributions of ultimate loss，outstanding claims reserves and IBNR are simulated. The proposed stochastic reserve development methods based on the correlation not only consider the correlation between the paid payments and the incurred payments，but also reflect the development difference of incurred and reported outstanding claims reserves in different accident years.Such ideas and methods considering correlation have important theoretical significance and practical value for multivariate reserving.

stochastic reserve development methods；multivariate reserving；Copulas function；Bootstrap method；bivariate normal distribution；predictive distribution

F840.4

：A

1003-207（2014）04-0009-08

2011-08-09；

2014-02-06

国家自然科学基金面上资助项目（71271121）；中央高校基本科研业务费专项资金（NKZXTD1101）

段白鸽（1983-），女（汉族），山西临汾人，复旦大学经济学院教师，博士，师资博士后，中国准精算师，研究方向：精算与定量风险管理、不确定经济学.