一种新的WIMAX标准LDPC码的软判决译码算法

李万臣, 王茂朝

哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001

一种新的WIMAX标准LDPC码的软判决译码算法

李万臣, 王茂朝

哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001

WIMAX标准下的LDPC码采用准循环编码方式，其译码多为和积（SP）译码算法。为了进一步降低译码复杂度，通过大量仿真分析获得最优乘性因子的值，并推导出近似线性公式，提出了一种改进型的归一化最小和(MNMS)算法。在此基础上，与校验节点匹配(CNM)算法相结合，进一步提高译码性能。仿真结果表明，这种新算法相比归一化最小和(NMS)算法、抵消最小和(OMS)算法、校验节点匹配(CNM)算法，其译码性能有明显改善，性能几乎接近和积（SP）译码算法。

WIMAX标准LDPC码；改进型归一化最小和算法；和积算法；校验节点匹配算法

低密度奇偶校验码（low density parity check codes, LDPC）[1]是由Gallager博士在1962年首次提出。随着近代硬件水平的飞速发展，Mackay[2],Spielman[3]等人对LDPC码进行了深入研究。LDPC码相比Turbo码，具有抗突发差错特性，避免可能带来的时延，性能更接近香农限，已成为当前研究的热点[4]。全球微波互联接入WIMAX[5](Worldwide Interoperability for Microwave Access)也将LDPC编码用做其信道编码的方案之一。

LDPC译码中的和积译码算法是一种软判决译码算法，能获得很好的性能，但是其译码复杂度高，不便于硬件实现。文献[6]中提出了2种改进型最小和算法，在校验节点更新时引入乘性因子α，提出归一化最小和算法；引入加性因子β，提出抵消最小和算法。为了简化，校验因子取常数。但实际上校验因子的值随着信噪比的不同应该有所改变。文中通过大量仿真，分析推导出WIMAX标准LDPC码随信噪比变化乘性因子的计算公式，提出一种新的改进型归一化最小和算法，同时结合文献[7]中提出的校验节点匹配算法提出一种新的软判决译码算法。仿真结果表明，这种新算法的译码性能更加接近和积译码算法。

1 和积译码算法

和积译码算法是一种基于置信传播的迭代软判决译码算法，其步骤如下。

1）初始化。

假设信道传递给信息节点的初始概率消息为L( pi)，(i=1,2,…,N)。计算L( pi)的值，对于每一个信息节点为i和与其相连的在集合C( i)中的校验节点j，设定变量节点传向校验节点的初始消息为L(0)(q)=L( P)=2y/σ2

ijii

2）迭代处理。

a）校验节点的消息处理。

对所有校验节点j和与其相邻的在集合R( j)中的信息节点i，第l次迭代时，通过信息节点判断校验节点的消息

b）信息节点的消息处理。

对所有信息节点i和与其相邻的在集合C( i)中的校验节点j，第l次迭代时，通过校验节点判断信息节点的消息

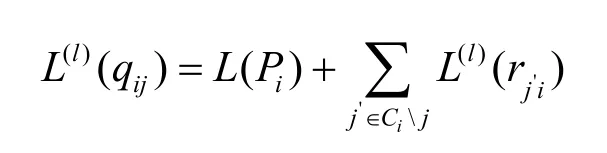
c）译码判决。

对所有信息节点计算硬判决消息

若L(l)(q)＞0，则cˆ=0；否则cˆ=1。

i i i

3）停止。

如果达到最大迭代次数，或者对于矩阵H满足HcˆT=0，运算停止，否则继续进行迭代处理。

2 几种降低复杂度的译码算法

2.1 最小和译码算法

由式（1）用近似最小值代替得出判决公式：

最小和译码算法[8]可以大大减少和积算法的复杂度和存储容量，同时不需要对信道进行估计，可以省略σ2的计算，进一步降低运算量。

2.2 归一化最小和译码算法和抵消最小和算法

在最小和算法中计算校验信息L( rji)时，为表述方便，设式（1）和（2）中的L( rji)分别表示为L1、L2,L2相比和积算法中的L1过高估计了其幅值。特别是当βij之间相差很小时，这种误差会更大。

基于以上考虑引入乘性因子α得到归一化最小和译码算法

引入加性因子β得到抵消最小和算法

上述两种算法对信息节点处理时，引入了乘性因子和加性因子，在稍增加复杂度的情况下，最小和算法获得了更好的译码性能。

2.3 校验节点匹配译码算法

这种算法其复杂度在最小和算法的基础上仅略微增加，就能获得逼近和积译码算法的译码性能。

3 新的软判决译码算法

3.1 改进型归一化最小和译码算法

在最小和算法中，乘性因子α取小于1的数来校正校验节点的信息。通常来讲，乘性因子α一般取常数，所以归一化处理的性能由乘性因子α的取值来决定。但是实际上为了获得最优的性能，乘性因子α的取值应随着迭代次数和信噪比的变化而改变，可以考虑在稍微增加复杂度的情况下分析不同信噪比下乘性因子α的取值。

在AWGN信道下，采用BPSK调制，根据WIMAX标准给出的基校验矩阵，构造出码率为1/2、码长为2 304的QC-LDPC码。考虑误码率从10−1到10−6时，信噪比在0～4 dB，每隔0.5 dB取一个仿真节点，对应的乘性因子α在0.5～0.95，每隔0.5个单位取值仿真。在不同的信噪比情况下，误码率随α变化曲线如图1、2所示。

图1 0～2.0 dB误码率随乘性因子α变化曲线

图2 2.5～4.0 dB误码率随乘性因子α变化曲线

通过观察得到在不同信噪比下最优的乘性因子α如表1所示。

表1 不同信噪比下最优乘性因子α取值

可以看出最优乘性因子α的值随着信噪比的增加而相应的增加，并且可近似看成每当信噪比增加0.5 dB，乘性因子α也相应增加0.05。当信噪比小于0.0 dB，译码误码率在10−1数量级以下，不具备实际应用价值。所以从信噪比为0.0 dB考虑，此时的最优乘性因子α为0.55，具体算法实现如下。

定义ω=0.55，信噪比取样点数为S，则每个取样点中的增量:

当i=1:S时，设改进型归一化最小和算法的乘性因子为η，则η近似线性计算公式为

信噪比取样点数S的取值可在硬件实现复杂度和译码性能两者之间权衡，得到相对理想的取值。

3.2 改进型归一化最小和算法与校验节点匹配结合的新算法

校验节点匹配算法是根据每个校验节点相连的信息节点的数目来更新校验节点信息。而WIMAX标准中的LDPC是一种非规则的LDPC，即行重不同；因此考虑在改进型归一化最小和算法的基础上，在判决校验信息时，应用校验节点匹配算法来进一步优化译码判决。其算法相比和积算法有如下不同：

在校验节点的消息处理中，对所有校验节点j和与其相邻的在集合R( j)中的信息节点i，第l次迭代时，通过引入改进型归一化乘性因子η，当i=1:S时，同时结合校验节点匹配算法，得到通过信息节点判断校验节点的消息。

4 性能仿真与结果分析

图3 新算法与检验节点匹配算法性能比较

采用MATLAB与C语言相结合的仿真环境，在AWGN信道下，采用BPSK调制，根据WIMAX标准给出的基校验矩阵，构造出码率为1/2、码长为2 304的QC-LDPC码。对本文提出的新算法与校验节点匹配算法在上述相同条件下进行仿真，误码率性能曲线如图3所示。

通过图3可以看出，本文提出的新算法相比性能较好接近和积译码算法的校验节点匹配算法，在BER=10−5时，大约有0.08 dB的提高。

继续分析，归一化最小和译码算法和抵消最小和译码算法采用文献[10]给出的性能最优取值α=0.95和β=0.10。在上述相同条件下进行仿真，误码率性能曲线如图4所示。

图4 5种译码算法性能比较

可以看出和积算法与最小和算法之间相差约有0.3 dB，在BER=10−5时，本文提出的新算法相比最小和算法有大约0.25 dB的提高，而与归一化最小和算法和抵消最小和算法相比也有0.15～0.2 dB的提高，与性能优异但复杂度高的和积算法相差仅有0.05 dB。当信噪比高于3 dB时，本文提出的新算法与和积算法的误码率均为0。

5 结束语

通过对常用的LDPC软判决译码研究，在提出改进型归一化最小和译码算法的基础上，与校验节点匹配算法结合，得到了一种性能优异并且复杂度相对和积算法很低的新算法。仿真结果表明，这种新算法的译码性能相比归一化最小和算法、抵消最小和算法、校验节点匹配算法更加逼近和积译码的性能。

[1] GALLGER R G．Low-density parity-check codes[J]．IRE Trans on Imformation Theory，1962, 8(1): 21-26．

[2] MACKAY D J C, NEAL R M. Near Shannon limit performance of low density parity check codes[J]. Electronics Letters, 1996, 32(18): 1645-1646．

[3] LUBY M G, MITZENMACHER M, SHOKROLLAH M A M，et al．Expander codes[J]．IEEE Trans on Imformation Theory, 1996, 42: 1710-1722.

[4] 袁东风, 张海刚．LDPC码理论与应用[M]．北京: 人民邮电出版社, 2008: 64-66.

[5] 谢刚, 赵哲峰, 雷少帅, 等. WIMAX技术原理及应用[M]. 北京: 北京邮电大学出版社, 2010: 12-13.

[6] CHEN J，FOSSORIER M P C．Near-optimum universal belief propagation based decoding of low-density parity check codes[J]. IEEE Transactions on Communications, 2002, 50(3): 06-414．

[7] HOWARD S，SCHLEGEL C，GAUDET V．Degree-matched check node decoding for regular and irregular LDPCs[J]．IEEE Trans on Circuits and Systems, 2006, 53(10): 1054-1058．

[8] FOSSORIER MPC, MIHALJEVIC M, IMAI H. Reduced complexity iterative decoding of low-density parity check codes based on belief propagation[J]. IEEE Transactions on Communications, 1999, 47(5): 673-680.

[9] HOWARD S L, SCHLEGEL C, GAUDET V C. Degree-matched check node decoding for regular and irregular LDPCs[J]. IEEE Trans on Circuits and Systems II: Express Briefs, 2006, 53(10): 1054-1058.

[10] 于学明. LDPC码的研究及其在OFDM系统中的应用[D]. 哈尔滨: 哈尔滨工程大学, 2011: 32-36.

A novel soft decision decoding algorithm for WIMAX standard LDPC codes

LI Wanchen，WANG Maozhao

College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001,China

WIMAX standard LDPC is based on quasi-cyclic encoding, and the decoding usually uses the sum-product decoding algorithm. In order to further reduce decoding complexity, a novel modified normalized min-sum (NMS) algorithm is proposed in this paper. The optimal multiplicative factor is obtained by a lot of simulation samples and analyses, and the approximate linear formula is deduced as well. On the basis of it, combining with the check node degree-matched algorithm, the decoding performance is improved further. Simulation results indicate that the proposed novel algorithm improves the decoding performance greatly compared with the NMS algorithm, the offset min-sum (OMS) algorithm and check node degree-matched (CNM) algorithm, and the BER is very close to the sum-product algorithm.

WIMAX standard LDPC codes; modified normalized min-sum algorithm; sum-product algorithm; check node degree-matched algorithm

TN911.22

A

1009-671X（2014）01-0039-04

10.3969/j.issn.1009-671X.201211017

2012-11-19.

李万臣（1963-）, 男, 教授；王茂朝（1984-）, 男, 硕士研究生.

李万臣, E-mail: lwchen@hrbeu.edu.cn.