节点环流网络中的最大流算法
2014-05-15徐光联孙文新
徐光联,孙文新
鹤壁职业技术学院 电子信息工程学院,河南 鹤壁 458030
节点环流网络中的最大流算法
徐光联,孙文新
鹤壁职业技术学院 电子信息工程学院,河南 鹤壁 458030
为了求出节点有容量并有存储功能的网络中的最大流,提出使用改进的带有节点环流的网络模型。在改进的网络模型中,网络节点改由新的结构代替,即节点分为入点和出点,增加中转弧和节点环。提出了进出节点的配平算法,使用了改进的流量守恒约束,通过虚拟源、虚拟汇进行配平,使用最大流算法求出由节点环流调节过的最大流。在配平算法中,遇到入流容量小于出流容量,要判断节点环流量的大小;遇到入流容量大于出流容量,要判断节点环流的残容量大小。算法应用于流的分配或流的汇聚。
网络流;节点环流;最大流算法;流量守恒
网络最大流是运筹学重要的内容,一般是在连通无环弧的s-t网络[1]中应用的,如运输电网、油气管线、通信网络等。常用的组合算法有标号法、Dinic法、推拉流算法等;常用的线性规划算法有网络单纯形法、网络内点法[2-3]等。网络中弧有容量,但是节点无容量。为了解决节点有容量的问题,可以使用节点分裂法[4-5],通过把有容量的节点分裂成2个点并在其中加入一条边,从而将节点和边都为有容量的问题转化为仅边有容量的问题,但这种转化可能破坏了网络的平面性。文献[6-7]分别给出了在不破坏网络的平面性条件下,将节点和边都有容量约束的无向平面网络和有向平面网络最大流问题转化为仅有边容量约束的网络最大流问题,然后采用网络最大流算法求解,但这些转化方法复杂,实现有一定困难。文献[2-3]引入人工智能中搜索的方法,根据网络可行流分解定理,在组合算法基础上,提出了网络最大流新算法。上述方法都保持了网络中节点之间的平等性。这里给出一种扩展的带有节点环流的NIO网络,一方面能够继承原来的理论,另一方面可以更简单地处理节点有容量的实际问题。
1 N网络和NIO网络
1.1 N网络模型
常用的N网络流模型[1]定义如下。
定义1设N是一个单源单汇网络,N=(V,A,s,t,C),是一个有向简单图。其中V是节点集合,A是有向边(弧)集合,s∈V是源点,入度为0,t∈V是汇点,出度为0。C是定义在弧集A上的一个非负容量函数。如果节点vi、vj∈V,称弧(vi,vj)中vj为弧头,vi为弧尾;弧上的容量记为C(vi,vj),弧上的流量记为f(vi,vj)。称这种带源点和汇点的网络为容量网络。
为了叙述方便,符号C(vi,vj)可简记为C(i,j)或Cij,流量f(vi,vj)记为f(i,j)或fij;源点s和汇点t为vs、vt的简写;V–{s,t}中的节点称为中转点。给定一个网络N,约定V中的节点个数为|V| = n,弧集A中弧的个数为|A|=m。
定义2如果流f定义在网络N上[4-5],满足下述条件:

1.2 扩展的NIO网络及其节点构造
在一个有向图D=(V,A)中,如果D中有重弧,节点有容量和自环,则不符合网络N的要求,通过一个转换把其构造成为一个有向简单图,转换原则如下。
1)重弧合并原则。如果 vi、vj∈V,且vi到vj有l条有向(重)边,则可合并为一条弧,记为aij。
2)节点分开原则。节点有容量也有自环,如图1所示。
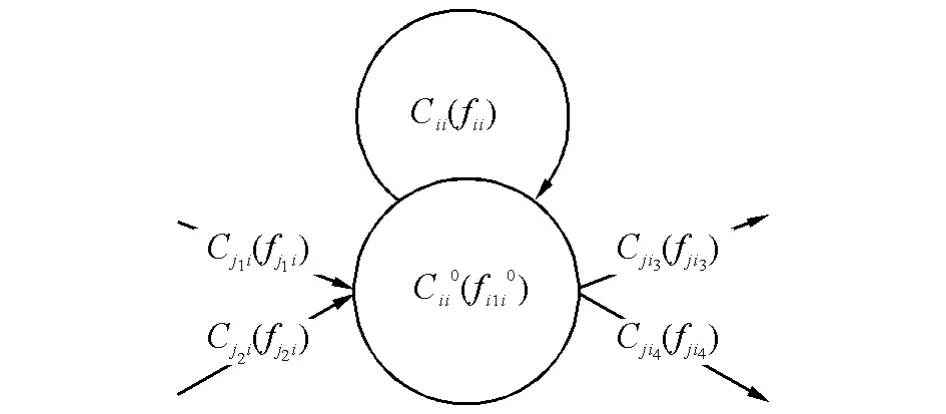
图1 N网络节点
自环记为aii=(vi,vi),环有容量,记为Cii环,环有流量,记为fii环,节点的进出容量(进出流量)记为Cii0(fii0)。把节点分开为入点vi−和出点vi+时,如图2所示,从入点vi−到出点vi+有一条定向连接弧,记为弧(vi−,vi+),其容量(流量)就是Cii0(fii0)。自环(vi,vi)上的容量(流量)是Cii(fii),分开为2条,一条是从vi−到vi+,是环的正向重弧(vi−,vi+),另一条是从vi+到vi−,是环的反向弧(vi+,vi−)。节点分开后,定向连接弧与环的正向重弧同向。根据重弧合并原则,设环的正向弧上的环流容量(流量)为Cii+(fii+);环的反向弧的环流容量(流量)为Cii-(fii-),正、反向弧上的环流容量(流量)数值大小相等而方向相反,因为Cii0(fii0)表示定向连接弧的容量(流量)。根据转换原则中的重弧合并规定,同向弧流合并,称为中转弧,记为Ci(fi),其中Ci=Cii++Cii0,fi=fii++fii0。合并后的结果如图3所示。
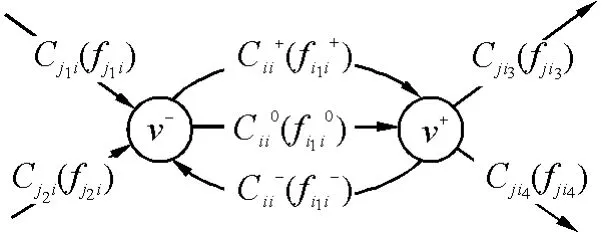
图2 网络节点分开示意
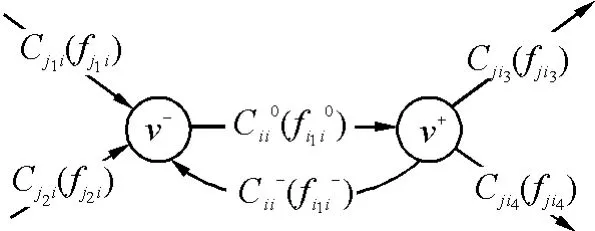
图3 NIO网络节点
NIO节点构造:原来的节点v被v+、v−这2个点替代,产生了2条新弧,所有的入弧连接到vi−,所有出弧从vi+向外连接,则入点vi-有唯一的一个出弧指向出点vi+,即中转弧。如果节点没有自环,则定义节点自环的容量(流量)记为0(0)。若有多个自环,则合并成一个。显然,有以下定理:
定理1 根据重弧合并和节点分开原则,所构造出的有向图是一个有向简单图[8]。
定义3 设 N=(V,A,s,t,C)是定义1中的网络,要表示N中节点的容量和环流,根据节点分开原则构造扩展网络[8]:NIO=(V−,V+,A,s−,s+,t−,t+,C),其中V−、V+是V中节点分开后的入点集和出点集,A是扩展后的有向边(弧)集,s−、s+是源点s分开后的源点入点和源点出点,t−、t+是汇点t分开后汇点的入点和汇点的出点,C是扩展后有向边(弧)上的容量函数。
扩展网络矩阵:NIO网络对应的邻接矩阵记为MIO,其元素是入点和出点组成的弧集,其子域可由弧上的容量(流量)等权值元素组成。
MIO中的弧集由集合:(V−∪V+∪{s−,s+,t−,t+})×(V−∪V+∪{s−,s+,t−,t+})中的元素表示。NIO网络中,所有可能出现的弧所表示的矩阵MIO如下所示。
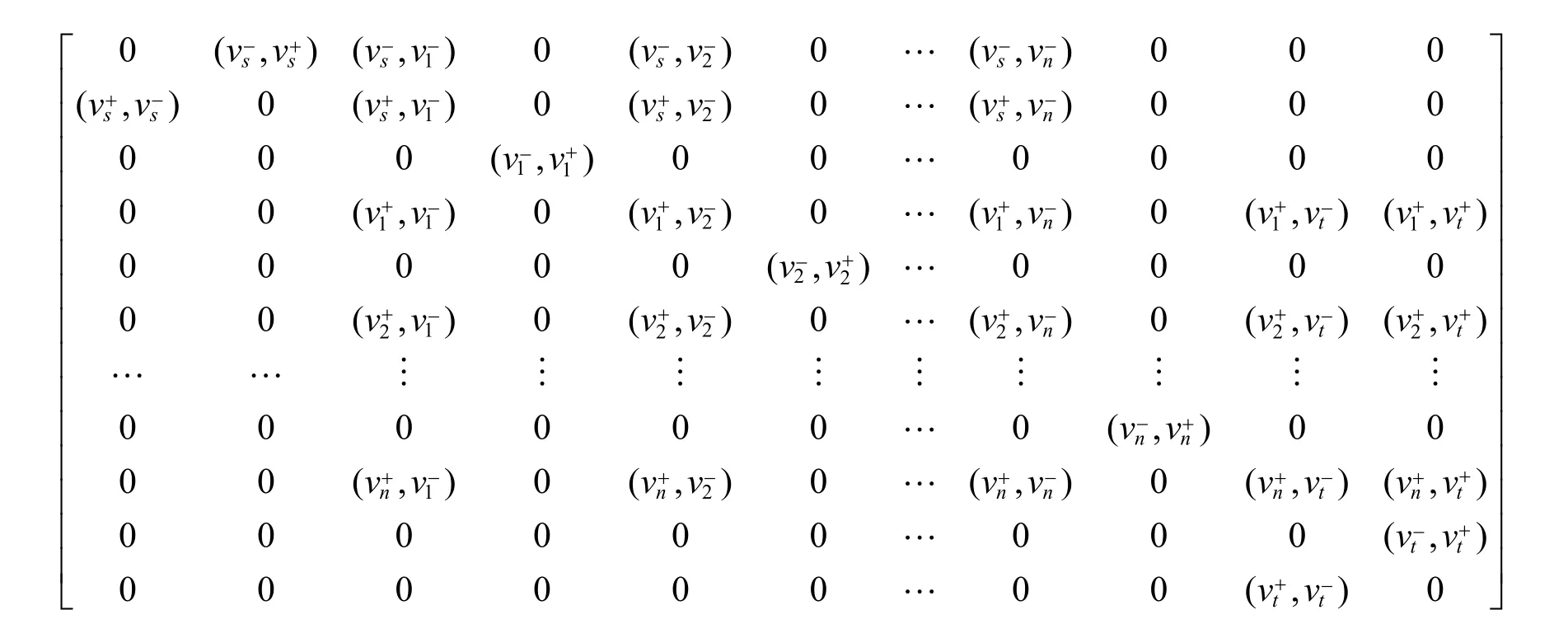
注1:MIO中的弧(vs-,vi-),(vi+,vt+), i=1,2,…,n,在正常情况下,它不存在,在特殊情况下使用,例如虚拟源或虚拟汇。2:MIO中的弧为0表示弧不存在,因而不使用。
1.3 节点的虚拟源与虚拟汇
根据可行流的守恒条件,对于除源点和汇点外的中间点vi,流入和流出应该相等而产生平衡,但实际上有很多情况下是不平衡的,为了平衡流量[8-9],使用以下定义:
定义4 在NIO网络中,增加从源点入点到中间点入点的辅助弧和流:f(vs−,vi−)称为虚拟源,C(vs−,vi−)称为虚拟源容量;增加从中间点出点到汇点出点辅助弧和流:f(vi+,vt+)称为虚拟汇,C(vi+,vt+)称为虚拟汇容量。
2 容量配平与最大流
2.1 NIO网络中节点环流
节点环流定义背景:如果网络表示河流网,则河流为弧,水库为节点,水库中的水为节点环流,水库的容量为节点环流容量,洪水来临时水库可滞流,干旱时期水库可放水浇田,水库起调节作用。由此背景,定义节点环流参与最大流算法的容量调节算法。N网络要求可行流遵守流量守恒约束,而在改进的NIO网络中,使用改进的流量守恒约束,也就是配平算法。根据入流、出流平衡分为3种情况,即:入流容量小于出流容量(又分为环流足、环流不足2种情况);出入流平衡;入流容量大于出流容量(又分为环流容量足、环流容量不足2种情况)。在这个算法中,节点的中转流容量设为足够大,即不起约束作用(另文讨论起约束作用),主要起作用的是环流容量、环流量。
2.2 节点入流容量小于出流容量的配平算法
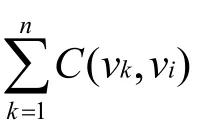

这意味着环流储备用尽。简记为:“入流小环流不足”。
3)配平后的出流容量maxC(i, j)配平后:
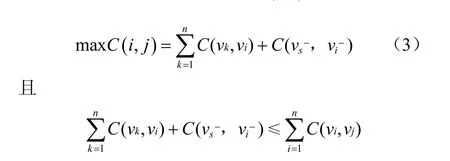
4)容量配平计算过后,再计算最大流。
如果网络中沿s-t方向的弧容量是递增的,则节点环流不断流出,成为一种汇聚流,用公式(1)~(3)。
2.3 节点入流容量等于出流容量
入流容量等于出流容量,则已经配平,简记“出入流已平衡”,这是一般的可行流情形。
2.4 节点入流容量大于出流容量
对于节点vi,设虚拟汇容量为C( vi+,vt+),虚拟汇为f( vi+,vt+),又设残容量[9]为Cre(vi, vi),且Cre(vi, vi)=C( vi, vi)−f( vi, vi)。

如果网络中沿s-t方向的弧容量是递减的,则节点环流不断增加,成为一种分配流,用公式(4)~(6)。
2.5 配平算法举例
例1:已知图4(上行)属于“入流小环流足”型,C( vs, v1)=5,C( v1, vt)=8,C( v1, v1)=10,且f( v1, v1)=4。其NIO图如图5所示。即环流容量为10,流量为4。源s和汇t的中转流容量设为100,即在本例中,源与汇的能力设为足够大。
分析:例1中,沿s-t方向的弧容量有增加的,有减少的,这是一个综合性调剂的算例。
算法:图5中的节点环流容量(流量)=10(4),入流容量小于出流容量,即
C( vs, v1)=5<8=C( v1, vt),
差值
Δ=C( vs, v1)−C( v1, vt)=5−8=−3
且−3≤4=环流量。所以虚拟源容量、流量均为−3=3,记为3(3)。在配平后的图中,最大流为8。计算后的节点环流原来是4,作为源,流出3,剩下了4-3=1。
例2:如图4(下行),是“入流小环流不足”型:C( vs, v1)=5,C( v1, vt)=8,C( v1, v1)=10,且f( v1, v1)=2。其NIO图如图5所示,即环流容量为10,流量为2。
算法:图5中的节点环流容量(流量)=10(2),C( vs, v1)=5<8=C( v1, vt),差值
Δ=C( vs, v1)−C( v1, vt)=5−8=−3,
且
−3>2=环流量;
所以虚拟源容量、流量均为环流量2,记为2(2)。在配平后的图中,最大流为7,其中节点环流2,作为源,流出2,剩下2-2=0。
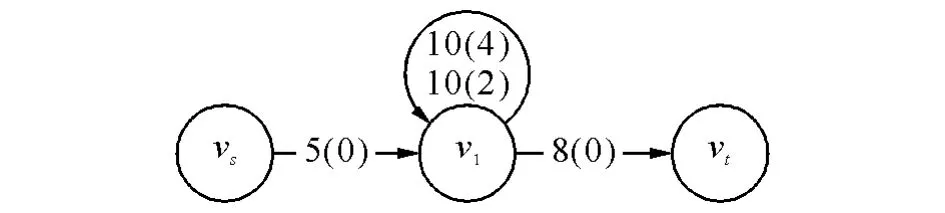
图4 N网络入流容量小于出流容量
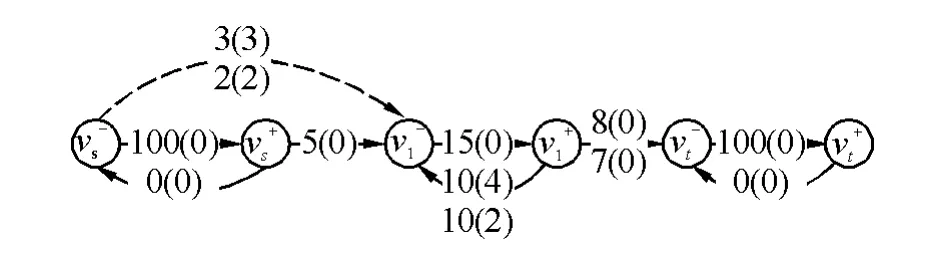
图5 NIO网络入流容量小于出流容量
例3:图6(上行)属于“入流大环容足”型,节点环流容量(流量)=10(6),其NIO图为图7。
算法:由于C( vs, v1)=8>5=C( v1, vt),差值
Δ=C( vs, v1)−C( v1, vt)=8−5=3
且
Δ=3≤4=10−6=环容量−环流量=残容量
即
Δ≤Cre(vi, vi)=C( vi, vi)−f( vi, vi)=10−6=4则令C( vi+,vi+)=f( v1+,vt+)=Δ,所以虚拟汇容量、流量均为=3,记为3(3)。在配平后的图中,最大流为8,其中节点环流为6作为源,滞流为3,故环流为6+3=9<10=环容量10。
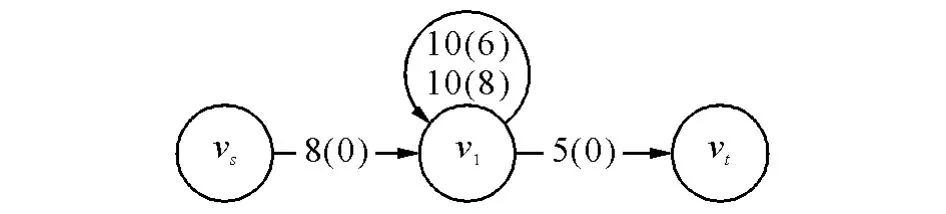
图6 N网络入流容量大于出流容量
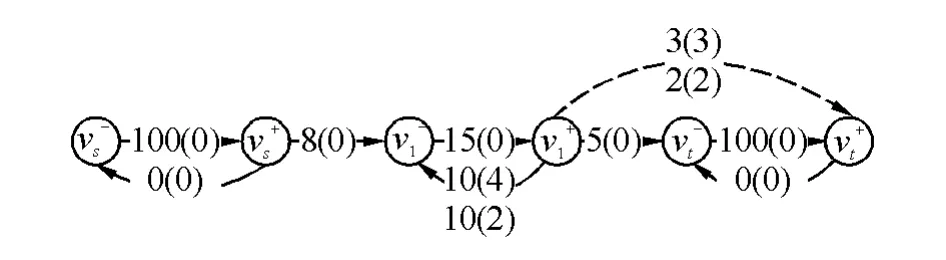
图7 NIO网络入流容量大于出流容量
例4:图6(下行)中“入流大环容不足”的情形为节点环流容量(流量)=10(8),其NIO图为图7。
算法:由于C( vs, v1)=8>5=C( v1, vt),差值
Δ=C( vs, v1)−C( v1, vt)=8−5=3
且
Δ=3>2=残容量=环容量−环流量=10−8
即
Δ=3>Cre(vi, vi)=C( vi, vi)−f( vi, vi)=10−8=2
则令:C( vi+,vt+)=f( vi+,vt+)=Cre(vi, vi)=2。所以虚拟汇容量、流量均取残容量,值为=2,记为2(2)。在配平后的图中,最大流为7,其中节点环流8,作为汇,滞流2,故环流为8+2=10,达到环流最大值,不能再增加。
3 综合应用举例
例5:如图8所示N网络图,节点有环流,数据见图。通过环流调剂,求其最大流。
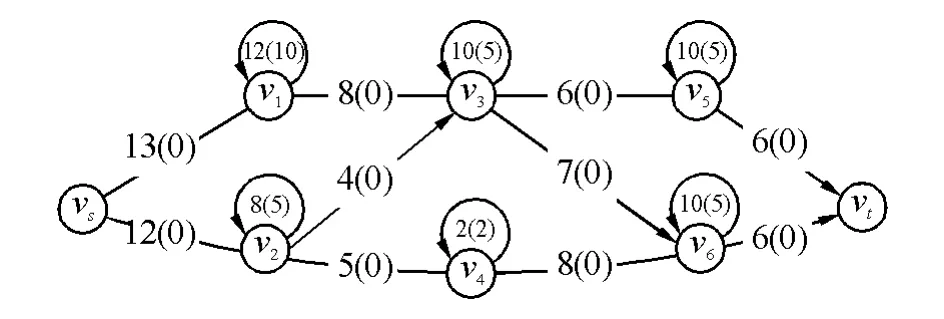
图8 N网络图例
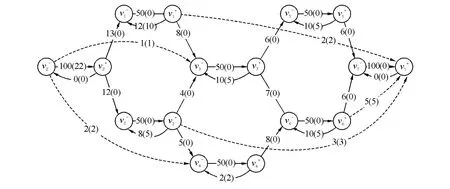
图9 NIO网络图例题
图8是N网络下的图,所对应的NIO网络图如图9所示,通过虚拟源、汇配平如图9中虚线所示。
算法:进行容量配平。
对于v1,入流容量=13>8=出流容量,Δ=13-8=5,环流容量(流量)=12(10),残容量为12-10=2,则Δ>2,是“入流大环容不足”型,设虚拟汇为残容量2(2)。
对于v2,入流容量=12>4+5=出流容量,Δ=12-(4+5)=3,环流容量(流量)=8(5),残容量为8-5=3,则Δ=3,是“入流大环容足”型,设虚拟汇为残容量3(3)。
对于v3,入流容量=8+4<6+7=出流容量,Δ=(8+ 4)-(6+7)=-1,环流容量(流量)=10(5),环流量5>|-1|= |Δ|,是“入流小环流足”型,设虚拟源数值为|Δ|,即1(1)。
对于v4,入流容量=5<8=出流容量,Δ=5-8=-3,环流容量(流量)=2(2),环流量2<|-3|=|Δ|,是“入流小环流不足”型,设虚拟源数值为环流量,即2(2)。
对于v5,入流容量=6=出流容量,是“入流出流平衡”,不用配平。
对于v6,入流容量=7+8>6=出流容量,Δ=15-6=9,环流容量(流量)=10(5),残容量为10-5=5,则Δ>5,是“入流大环容不足”型,设虚拟汇为残容量5(5)。
这样容量配平完成,虚拟的源和汇已经标定,这样,用最大法计算出最大流为22。
对比节点环流变化如表1所示。
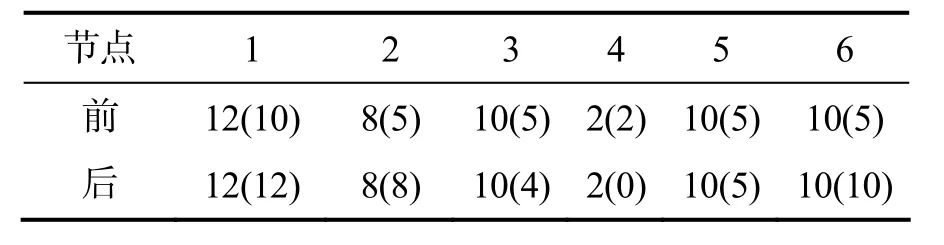
表1 节点环流变化表
讨论:例5中,源12+13=25,25-1-2=22,汇=6+ 6=12,12+2+5+3=22,符合最大流算法。
4 结束语
带有节点环流的NIO网络中,其节点环流可以调节弧上的流量,是计算最大流的根据,这是一个创新点,它是从河流与水库的关系中抽象出来的,符合实际情况。而NIO网络又是N网络的改进,其节点结构符合现代流通网络中节点的进、出、储存、转发等应用功能;可利用其MIO矩阵可进行统计分析等计算等,因而,可作为应用研究的课题另文讨论。运用节点环流容量、流量配平出来的虚拟源、虚拟汇,满足了最大流计算的条件,而限制中转流容量,并把节点环流容量、流量设为0,就成为点和边有容量约束的另一种处理节点的有容量网络。而不限制节点中转容量,且把节点环流容量、流量设为0,就成为一般N网络。NIO网络能够成为异常处理的模型[10]且应用广泛。所以说NIO网络继承了N网络的功能,是一种改进的性能更好的网络。
[1] 高随祥. 图论与网络流理论[M]. 北京: 高等教育出版社, 2005: 292-293.
[2] 厍向阳, 罗晓霞. 点和边有容量约束的网络最大流新算法[J]. 计算机应用, 2008, 28(1): 143-145.
[3] 厍向阳. 点和边有容量约束的网络最小费用最大流算法[J].计算机应用研究, 2010,27(8): 3112-3154.
[4] 王朝瑞. 图论[M]. 3版. 北京: 高等教育出版社, 2005: 292-293.
[5] 张先迪, 李正良. 图论及及其应用[M]. 北京: 高等教育出版社, 2005: 251-253.
[6] 张宪超, 万颖瑜, 陈国良. 一类实际网络中的最小截算法[J].软件学报, 2003, 14(5): 885-890.
[7] 张宪超, 江贺, 陈国良. 节点和边都有容量的有向平面网络中的最小截和最大流[J]. 计算机学报, 2006, 29(4): 543-551.
[8] 徐光联. 节点有自环的网络流数学模型[J]. 数学的实践与认识, 2011, 9(17): 148.
[9] J 邦詹森, G 古廷. 有向图理论、算法用应用[M]. 姚兵, 张辅忠, 译. 北京: 科学出版社, 2009: 87-88.
[10] 徐光联, 尚亚蕾. 网络系统异常处理的数学模型[J]. 科学技术与工程, 2010, 5(14): 123-124.
Maximum flow algorithm in network with node loop
XU Guanglian, SUN Wenxin
School of Electronic Engineering, Hebi College of Vocation and Technology, Hebi 458030, China
In order to search maximum flow in the network with node capacity and node memory function, a network model with the node loop is proposed. The node of the network is substituted by the new structure of the node in the improved network, which is divided into enter-flow point and out-flow point, and added with the transfer arc and node loop. A balancing algorithm is proposed for entering and leaving the node and the improved flow conservation constraints are used; using the virtual source and virtual sink of balance, the maximum flow regulated by the node loop is calculated. In the balancing algorithm, when the enter-flow capacity is less than the out-flow capacity, the node ring flow size should be determined; otherwise, the residual capacity of the node loop should be determined. The algorithm is applied to the distribution or convergence of flow.
network flow, node loop flow; maximum flow algorithm; flow conservation
O157
A
1009-671X(2014)01-0048-06
10.3969/j.issn.1009-671X.201306011
2013-06-08.
河南省基础与前沿技术研究项目(122300410258).
徐光联(1954-), 男,副教授;孙文新(1966-), 女,副教授.
孙文新,E-mail: sunwxin126@126.com.
