二维线性大间距判别分析及其在步态识别中的应用

张鹏，付希凯，葛国栋，贲晛烨

山东大学 信息科学与工程学院，山东 济南 250100

二维线性大间距判别分析及其在步态识别中的应用

张鹏，付希凯，葛国栋，贲晛烨

山东大学 信息科学与工程学院，山东 济南 250100

提出一种二维线性大间距判别分析（Two dimensional linear maximum margin discriminant analysis,2DLMMDA）的投影算法。该算法一方面采用了有效且稳定的大间距优化准则，引入了Laplacian矩阵，保持了特征矩阵的流形结构，且优化域为Laplacian类间散度与Laplacian类内散度之差，能克服Fisher准则带来的小样本问题；另一方面，采用了具有监督信息的判别分析，大大地提高了识别率。为了验证所提出的算法对特征提取的有效性，选择最近邻分类器进行特征分类，最后通过在CASIA(B)步态库上实验。实验结果表明，文中提出的算法具有更高的识别率和识别速度。

特征提取；二维线性大间距判别分析；拉普拉斯矩阵；步态识别

在计算机视觉和模式识别领域，降维技术一直是众多研究者热衷的焦点[1]。数据的高维性给数据处理带来了很大的难度，对硬件设备有很高的要求[2]。自一个多世纪前K. Pearson提出主成分分析（principle component analysis，PCA）[3]方法后，几十年来数据采集和存储能力得到快速提高，大数据处理渐渐走向日常应用，行之有效的特征提取技术也越来越迫切。近几十年来，经典的降维技术，例如PCA、独立成分分析（independent component analysis，ICA）[4-5]、线性判别分析（linear discriminant analysis，LDA）[6]受到了严重的挑战，已经不能继续满足日常应用中对大数据处理的有效性和可靠性要求。在这种严峻的形势下，研究者对于2D数据进一步研究，为了保持二维数据的完整性，提高执行效率和准确率，Yang 首先提出了直接处理二维矩阵的方法替代经典算法中将矩阵转化为一维向量来处理图像矩阵的方法。继二维主成分分析(Two dimensional principle component analysis，2DPCA)[7]之后相继提出了二维线性独立判别分析（Two dimensional linear discriminant analysis, 2DLDA）[8-9]、二维局部保留投影（Two dimensional locality preserving projects，2DLPP）[10]以及二维大间距算法[11]等算法，大大提高了运算的效率。

研究表明，PCA是一种无监督的降维技术[3]。2DPCA对PCA进行了改进，将二维图像矩阵直接进行投影，而不是把二维矩阵先初始化为向量，大大提高了识别的准确率，然而二者都是无监督方式，分类可靠性还有很大的局限性。而2DLDA算法用样本的标号信息作为监督矩阵指导降维，取得了更好的分类效果。然而2DLDA采用Fisher判别准则最大化类间散度和类内散度之商，需要计算类内散布矩阵的逆，而小样本将导致奇异的类内散度矩阵，因此2DLDA带来了小样本问题（small sample size, SSS）[12]。

近几年来，LPP[13]用于降维备受研究者亲睐，它是一种基于流形假设提出的流形学习方法的线性算法[14]，通过保持数据的局部性的Laplacian矩阵来实现降维，在步态识别领域取得了不错的效果。类似PCA改进到2DPCA的过程，2DLPP被提出，对图像矩阵直接投影，而不是将其转化成向量。2DLPP保留了LPP的优点，不仅能解决奇异矩阵导致的小样本问题，并且不需要PCA进行预处理，保留了二维图像数据的结构信息，获得了更好的识别率。2DLPP可以解决一般性的特征值问题，但也带来了一系列的问题。首先，2DLPP涉及到相似矩阵，相同的相似矩阵值与LPP内部流形结构矛盾，且高维训练样本处理起来非常麻烦，容易造成维数灾难，对物理设备有更高的要求；其次，需要引入大量的系数用于图像处理和识别，稀系数的优化选取有很大的难度。

步态识别具有易采集、不易伪装、采集设备要求低等优点，是最具有潜力的生物特征之一[15]。随着生物特征识别技术的迅速发展，对步态识别的研究出现了很多成果[16]。步态能量图[17]是近年来提出的一种有效的步态识别方法，它受轮廓噪声影响小，结合空间降维技术[18]可有效地提取步态能量特征。

鉴于2DLDA解决分类问题的有效性，文中提出了一种二维线性大间距判别分析的特征提取算法。该算法不仅引入了Laplacian矩阵，保持了数据之间的流形结构，而且优化类间散度与类内散度之差，克服了小样本问题。同时，它采用判别分析，可以获得更高的识别性能。通过在中科院CASIA（B）步态库上实验，实验结果证明本文的方法鲁棒性强，具有更高的识别率和识别速度。

1 二维线性大间距判别分析

设矩阵x表示一幅大小为m×n的图像，U表示一个大小为m×m′( m′≤m)的行投影矩阵，y为提取的特征矩阵，图像x经过线性变换投影得到：

因此，图像大小由原来的m×n，变为m′×n，实现了降维的目的，其中最佳投影矩阵U可以根据特征矩阵y的Laplacian散度情况来确定，表示如下

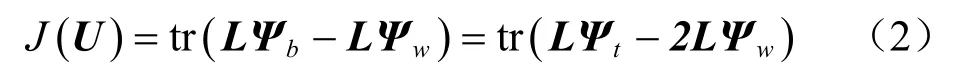
式中：LΨb表示类间Laplacian散度矩阵；LΨw表示类内Laplacian散度矩阵；LΨt表示总体Laplacian散度矩阵；tr(⋅)表示表达式的迹，式（2）取得最大值的物理意义是：找到一个最佳的投影矩阵U，使得投影后所得特征向量的列间Laplacian类间距最大化。在特征空间中，上述间距越大，就代表不同类中的样本距离间隔越远，而同类中的样本间距就会越近。即优化目标式（3）最大

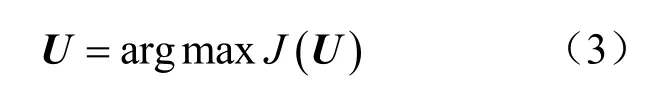
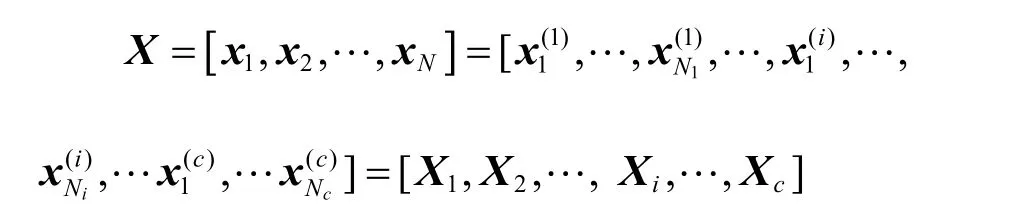
相应地，令yi表示特征xi投影后的特征矩阵，则特征提取后构成的矩阵为

为了保持步态图像的内在非线性流形结构，在散度矩阵中引入Laplacian矩阵的高斯相似性[19]：

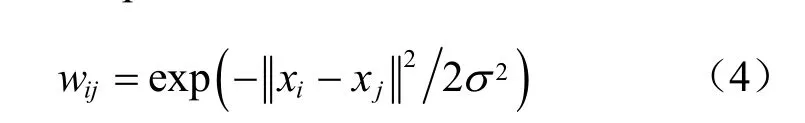
图像集X的总体Laplacian散度定义如下：

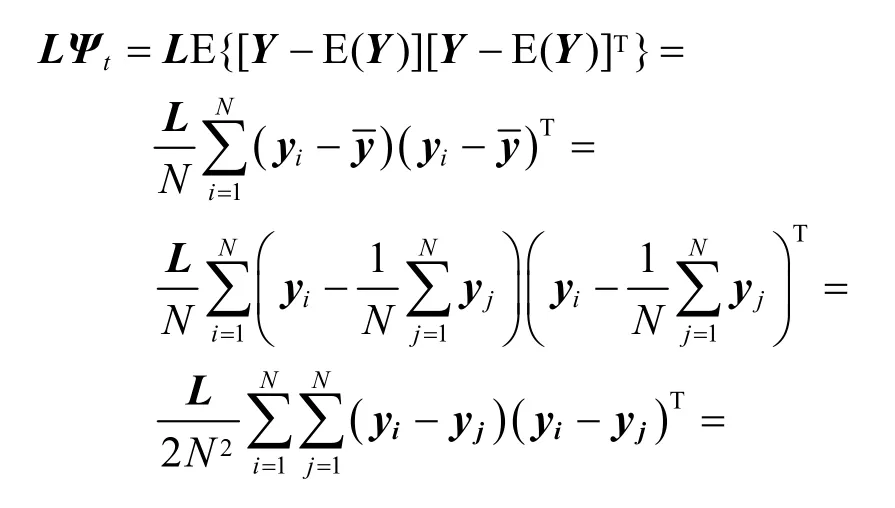
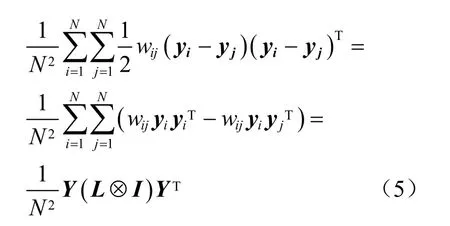
对投影矩阵强加正交性约束，则最优U通过求解如下的优化问题获得：

通过（10）、（13）两式得到基于Laplacian矩阵的二维线性大间距判别分析是将大小为m×n目标图像矩阵xi同时在投影矩阵Um×m′和Vm′×n上进行投影，得到一个m×n的矩阵zi，如式（14）所示。

2 分类识别

给定一个测试图像xtest,由式（16）可得该测试图像的特征矩阵ztest

文中采用最近邻分类器验证所提出算法的特征提取的有效性，通过计算训练样本和测试样本特征值之间的欧氏距离进行分类，如式（18）：

式中d(ztest,zi)为测试图像的特征值矩阵与训练样本集中各样本的特征矩阵之间的欧氏距离。当测试样本与样本库中的某一个样本之间有最小的欧氏距离时，则认为该测试样本与步态样本库中的相应样本匹配。如果该测试样本与样本库中相应的样本属于同一类，则认为是匹配正确的，否则，认为该测试样本与样本库中相应步态样本是匹配错误的。

3 实验结果

CASIA（B）步态库是中国科学院自动化研究所于2005年1月建立的一个步态轮廓数据库，它是一个多视角的步态库，在帧频25帧/s摄像机下获得。库中共包括124个人，每个人有3种行走条件（其中正常行走拍摄6次、背包情况下拍摄2次、穿着外套拍摄2次），每个人在3种条件下都按照11个视角（0˚，18˚，36˚，…，180˚）进行采集。

为了验证2DLMMDA算法的识别效果，将2DLMMDA方法在CASIA(B)步态库90˚视角上的步态下进行了测试。PC机的配置为Intel(R) Core(TM)2 Duo CPU T5870 @2.00GHz，2.00GB内存的PC机上进行实验。在正常行走状态下，对每个样本分别提取步态能量图特征，大小归一为64×64像素，如图1所示为CASIA(B)库中3个研究对象的步态序列能量图。

图1 CASIA（B）库中提取的3个人的步态序列能量

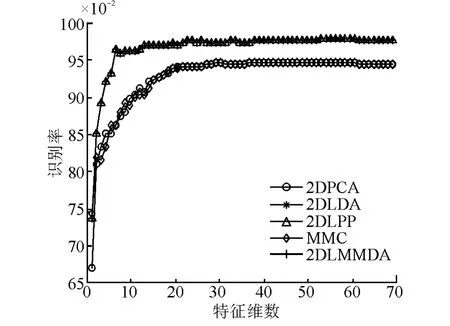
图2 不同特征维数下的识别率变化

在实验中，首先从提取的步态序列库中对每个人随机选取3个样本用于训练，剩下的3个样本用于测试算法的识别率和识别效率，为了保证算法的准确性，重复做10次实验，取识别率和识别时间的平均值作为最终结果，为了验证保留维数与识别率的关系，在图2中给出了保留不同维数下的识别率曲线，并在表1中给出了2DLMMDA算法与其他方法在最高识别率、识别时间以及相应的保留维数的对比情况。

实验结果表明，2DPCA，MMC这2种方法有较快的识别速度，但是识别率相对较低。这是由于2DPCA没有引入监督信息；而MMC虽然引入了监督信息，但是优化的是具有近邻流形结构的Laplacian散度差，而且仅为单边投影；2DLDA、2DLPP这2种方法虽然提高了识别率，但是也大大增加了计算负担，这是由于它们直接对大数据进行处理，优化Fisher域；而文中提出的2DLMMDA算法正好均衡了识别的有效性和鲁棒性，在尽量少的识别时间内，取得更高的识别率。由图2可知，在相同的特征维数的前提下，2DLMMDA总能取得最高的识别率，由表1可知，文中提出的2DLMMDA算法最高识别率96.51%，总的时间仅为18.63 s。

表1 2DLMMDA算法在CASIA（B）步态库实验结果及其与其他方法对比

4 结束语

文中提出了一种二维线性大间距判别分析的特征提取算法。该算法一方面在计算散度矩阵时引入了Laplacian矩阵，保持了数据间的流形结构，另一方面不再是优化Fisher域，而是优化类间Laplacian散度与类内Laplacian散度之差，克服了优化Fisher域带来的小样本问题。同时，该算法还引入了带有监督信息的判别方法，大大地提高了识别率。通过与同类方法相比，文中的算法在不明显增加识别时间消耗的基础上，取得了最高的识别率。但是，步态能量图结合二维线性大间距判别分析并没有考虑各帧之间的关系，而步态序列各帧却具有严格的时间顺序。随着多线性技术的发展，今后的工作是将步态序列在更高维空间中进行特征提取，将运用多线性技术将各帧之间的关系考虑进来，势必会得到更好的识别效果。

致谢

感谢中科院自动化所为我们提供的CASIA(B)步态数据库。

[1] CARREIRA-PERPINAN M A. A review of dimension reduction techniques[R]. Sheffield: University of Sheffield Tech. Rep CS-96-09, 1997: 1-69.

[2] FODOR I K. A survey of dimension reduction techniques[R]. Center for Applied Scientific Computing, Lawrence Livermore National Laboratory, 2002: 1-18.

[3] ABDI H, WILLIAMS L J. Principal component analysis[J]. Wiley Interdisciplinary Reviews: Computational Statistics, 2010, 2(4): 433-459.

[4] HYVÄRINEN A. Survey on independent component analysis[J]. Neural Computing Surveys, 1999, 2: 94-128.

[5] HYVARINEN A, KARHUNEN J, OJA E. Independent component analysis[J]. Studies in Informatics and Control, 2002, 11(2): 205-207.

[6] BELHUMEUR P N, HESPANHA J P, KRIENGMAN D J. Eigenfaces vs. Fisherfaces: recognition using class specific linear projection[J]. IEEE Trans Pattern anal Mach Intell, 1997(7): 711-720.

[7] YANG J, ZHANG D, FRANGI A F. Two-dimensional PCA: a new approach to appearance based face representation and recognition[J]. IEEE Trans Pattern anal Mach Intell, 2004, 26(1): 131-137.

[8] LI M, YUAN B Z. 2D-LDA: a statistical linear discriminant analysis for image matrix[J]. Pattern Recognition Letters, 2005, 26(5): 527-532.

[9] LI J, JANARDAN R, LI Q. Two-dimensional linear discriminant analysis[J]. Advances in Neural Information Processing Systems, 2004, 17: 1569-1576.

[10] CHEN S, ZHAO H, KONG M. 2DLPP: a two-dimensional of locality preserving projections[J]. Neuro Computing, 2007, 70(4/5/6): 912-921.

[11] LI H F, JIANG T, ZHANG K S. Efficient and robust feature extraction by maximum margin criterion[J]. IEEE Transactions on Neural Networks, 2006, 17(1): 157-165.

[12] RAUDYS S J, JAIN A K. Small sample size effects in statistical pattern recognition: recommendations for practitioners[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(3): 252-264.

[13] HE X F, NIYOGI P. Locality preserving projections[C]// Proceedings of the 16thConference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2003: 153-160.

[14] HE X F, YAN S C, NIYOGI P, et al. Face recognition using Laplacian faces[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2005, 27(3): 328-340.

[15] 贲晛烨，徐森，王科俊.基于Trace变换的步态识别算法研究[J]. 吉林大学学报: 工学版, 2012, 42(1): 156-160.

[16] 贲晛烨, 徐森, 王科俊. 行人步态的特征表达及识别综述[J]. 模式识别与人工智能, 2012, 25(1): 71-81.

[17] HAN J, BHANU B. Individual recognition using gait energy image[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(2): 316-322.

[18] BEN Xianye, MENG Weixiao, WANG Ze, et al. Two linear subpattern dimensionality reduction algorithms[J]. Journal of Harbin Institute of Technology: New series, 2012, 19(5):47-53. [19] BELKIN M, NIYOGI P. Laplacian eigenmaps for dimensionality reduction and data representation[J]. Neural Computation, 2003, 15(6): 1373-1396.

[20] 詹宇斌, 殷建平, 刘新旺. 基于大间距准则和图像矩阵双向投影的人脸特征提取方法[J]. 自动化学报, 2010, 36(12): 1645-1654.

2D linear maximum margin discriminant analysis and its application to gait recognition

ZHANG Peng, FU Xikai, GE Guodong, BEN Xianye

School of Information Science and Engineering, Shandong University, Ji’nan 250100, China

In this paper, a novel projection algorithm named 2D linear maximum margin discriminant analysis is proposed. The efficient and stationary maximum margin optimization criterion was used in this algorithm, which introduces Laplacian matrix in order to maintain the manifold structure of the feature matrix, and the optimization criterion is the difference of the Laplacian inter-class scatter and Laplacian intra-class scatter. This algorithm can avoid the small sample size (SSS) problem brought by the Fisher criterion. The discriminant analysis is adopted, which has supervision information and greatly improves the recognition accuracy. In order to verify the efficiency of the proposed method for feature extraction, experiment with the nearest neighborhood (NN) classifier on the CASIA(B) database is conducted. The results show that the proposed method gains a higher recognition rate and faster speed.

feature extraction; two dimensional linear maximum margin discriminant analysis; Laplacian matrix; gait recognition

TP391.4

A

1009-671X（2014）01-0011-05

10.3969/j.issn.1009-671X.201306002

2013-06-03.

国家自然科学基金资助项目（61201370）；高等学校博士学科点专项科研基金资助项目(20120131120030）；中国博士后科学基金面上资助项目（2013M530321）；山东大学自主创新基金资助项目（2012GN043，2012DX007）.

张鹏（1990-）, 男, 硕士研究生;贲晛烨（1983-）, 女, 讲师, 硕士生导师, 博士.

贲晛烨, E-mail: benxianyeye@163.com.