基于高阶模多象限法的微小平移测量

刘尊龙，孙恒信，刘奎，郜江瑞

（山西大学 光电研究所量子光学与光量子器件国家重点实验室，山西 太原 030006）

0 引言

精密测量技术是量子光学的重要应用之一。其中激光微小平移测量在诸多领域都有着重要意义，例如，现代信息光学中光学图像探测［1］、天文学中卫星之间的位置稳定［2］以及生物学中粒子运动追踪［3］等。随着科学的发展和认知的需求，对微小平移测量的精度（灵敏度）要求越来越高。通过产生空间非经典光场降低量子噪声［4－6］，可以提高灵敏度。然而，空间非经典光场需要在苛刻的实验条件下才能产生［7］，且易受传播损耗的影响而导致其灵敏度降低，这就需要我们寻找其他有效光源代替空间非经典光场。空间高阶模激光具有更加复杂的横向分布，包含更大的信息量，已经被应用于精密测量中［8－9］，因此，我们考虑将空间高阶模激光用于微小平移测量来提高测量灵敏度。

目前普遍采用的空间微小平移测量装置为平衡零拍系统［6，10－11］，但使用高阶模激光作为信号光时，平衡零拍系统需要构造复杂的本底光，不易实现。近年来半导体器件加工工艺取得了飞速发展，其中CCD探测器每个像素尺寸已经可以达到微米量级，可以用于探测横向分布更加复杂的光场，从而获取更大的信息量，多象限探测法逐渐成为一种有效可行的测量手段。

本文给出了一种基于高阶厄米高斯模的微小平移多象限探测方案，在量子噪声不变的情况下，通过提高信号光模式阶数可以大幅提高平移测量的信噪比，从而提高测量灵敏度，且实验装置更加简便有效。

1 激光微小平移探测的极限

激光具有很好的空间指向性，可以用来加载微小平移信息，通过测量其空间横向光子数分布，我们可以提取出平移信息。

对于一束厄米高斯TEMn0模激光，只考虑一维情况下，其横向光子数分布满足

TEMn0模经过微小平移d后，其空间分布泰勒展开为：

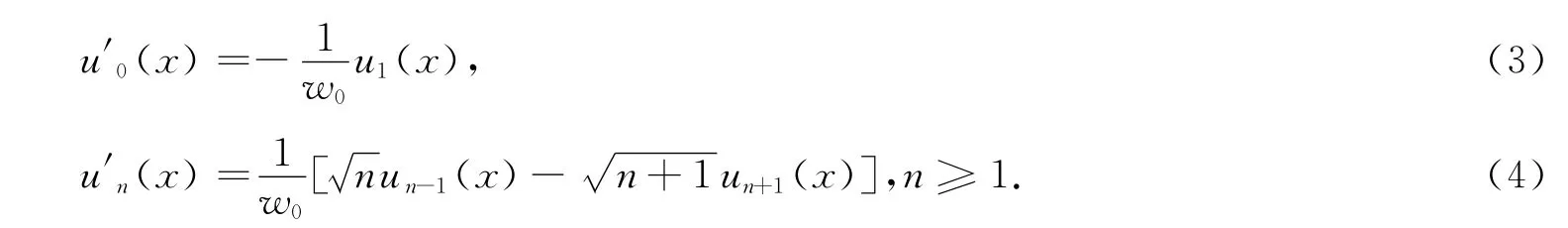
由于量子噪声的存在，在对激光进行测量时，空间横向每一处对应的光子数n（x）在时域上都是围绕其均值¯n（x）起伏的随机量，我们只能得到关于平移量d的一个估计量＾d，而且＾d必定伴随着量子噪声起伏。信息理论里定义了估计量＾d的起伏量的下界，即克拉美－罗下界（Cramer-Rao bound）［12］，对于高阶横模相干光场，其估计量＾d的克拉美－罗下界为：

IF称为Fisher信息，可以从量子噪声中分辨出的最小可测量值为dmin＝1／，则探测灵敏度极限为

由此可见，Fisher信息量越大，对平移量d可达到的探测精度越高。而Fisher信息量的大小与信号光横向分布有密切关系。分别将（3）式和（4）式带入（7）式，可以得到当信号光为TEMn0模时（n＝0，1，…），测量灵敏度极限为

这一极限不依赖于测量方式，只与信号光的模式分布有关，而相比于TEM00模，高阶模就具有更强的空间分布特性，测量灵敏度极限更大。

接下来我们考虑采用多象限探测法进行激光横向微小平移测量，分别给出采用厄米高斯基模和高阶模作为信号光情况下的测量灵敏度。

2 多象限法探测微小平移

2.1 理想模型

Fig.1 Experimental scheme of array detection for small displacement图1 多象限法探测微小平移实验方案

实验方案如图1所示，采用TEMn0模激光作为信号光（n＝0，1，…），信号光经过平移调制后，横向强度分布由多象限探测器每个象限测得，理想模型情况下，每个象限宽度都为无穷小，所有像素的测量信号分别取增益之后加和得到估计量S（d），S（d）可表示为以下积分形式

其中g（x）为对x处象限测得信号的增益，取适当增益使S（d＝0）＝N∫g（x）｜un（x）｜2d x＝0，将（2）式带入（9）式得，估计量S（d）为d的无偏估计量

定义探测模式w（x）＝g（x）un（x）／f，其中f2＝∫g2（x）｜un（x）｜2d x为归一化系数。

对于相干光，S（d）的量子噪声为探测模式对应的量子噪声即Δ2S＝Nf2［13］。

当增益取为g（x）∝gopt（x）＝u′n（x）／un（x）时，探测模式w（x）与归一化后的平移激发模式u′n（x）具有相同的空间分布，估计量S（d）的信噪比达到最大，为

2.2 实际模型

实际情况下，无穷小象限是不存在的，每个象限都为有限宽度的区域Di（i＝1，2，…）。通过理想模型，已经得到最佳增益分布gopt（x），按照gopt（x）分布来控制每个象限区域Di的增益。估计量S（d）可表示为以下加和形式

每个象限Di的宽度大小l直接影响着耦合系数，而耦合系数决定了探测灵敏度。设每个象限宽度为l＝ω0／k（k＝1，2，…），k值的大小决定着探测器对光斑分割的象限数，k值越大，参与联合测量的象限越多，可以获得的信息量越多。

我们分别模拟了采用TEM00模、TEM10模和TEM20模作为信号光的微小平移测量。图2分别给出了三种模式作为信号光进行微小平移测量时的信号光模式和激发模式横向分布及对应最佳增益分布，其中横轴为归一化坐标x／ω0，纵轴为归一化常数，实线为信号光模式分布，虚线为平移激发模式分布，点状虚线为最佳增益分布。图3为测量灵敏度随k值变化的趋势，其中纵轴为归一化的测量灵敏度SAD，n0／SCRB，00。

Fig.3 Plots of normalized sensitivities with TEM00 mode，TEM10 mode and TEM20 mode as signal light，as functions of k图3 采用TEM00模、TEM10模和TEM20模作为信号光的归一化测量灵敏度随k值变化

从图3中可以看出，随着k值逐渐增加，各阶模对应的测量灵敏度都逐渐增加，趋近各自的测量极限，而且使用高阶模相干光作为信号光时，可以达到基模灵敏度极限的倍。

当k取2时，相比TEM00模作为信号光，高阶模测量精度就有显著的提高，目前已经量产的Hamamatsu G7150-16多象限探测器的每象限宽度为l＝80μm，假设信号光腰斑大小为ω0＝160μm，功率为P＝1 mW，波长为λ＝1μm，分辨率带宽为RBW＝100 k Hz，采用TEM00模、TEM10模和TEM20模作为信号光最小可测量量分别可达0.37 nm、0.26 nm、0.23 nm，其中TEM10模和TEM20模作为信号光，比TEM00模测量灵敏度分别提高约42%和61%。

通过订制具有更小象限宽度的多象限探测器，目前最小CCD可达微米量级，可以使k值取到更大。当k取10时，各阶模测量灵敏度接近灵敏度极限，TEM10模和TEM20模作为信号光测量灵敏度分别比基模提高约65%和110%，而采用空间非经典光场作为信号光，想要达到同样的测量精度，需要分别产生4.3 dB和6.4 dB的空间压缩光［4，6］。此外，使用多象限探测器直接对高阶模激光进行探测，相比于平衡零拍探测，避免了产生复杂的本底光，且不需要位相的锁定。因此，高阶模多象限探测法在提高测量精度的同时，极大地简化了实验装置。

3 结论

相比于厄米高斯基模激光，采用高阶模作为信号光进行微小平移测量可以提高信噪比，n阶模测量灵敏度极限提高了倍。高阶模横向分布更加复杂，包含更多的信息量，针对这一特征，本文采用多象限探测法，即横向分布的多个象限联合测量，并且控制每个象限的增益使测量趋于最有效，数值模拟结果证明高阶模作为信号光，测量灵敏度有显著的提高。本文提出的高阶模多象限探测法，为激光微小平移测量提供了直观而又简便有效的方案。

［1］ Lugiato L A，Gatt Ai，Brambilla E.Quantum Imaging［J］.J Opt B：Quantum Semiclass.Opt，2002，4：S176-S183.

［2］ Nikulin V，Bouzoubaa M，Skormin V，et al.Modeling of an Acousto-optic Laser Beam Steering System Intended for Satellite Communication ［J］.Opt Eng，2001，40（10）：2208-2214.

［3］ Taylor M A，Janousek J，Daria V，et al.Biological Measurement Beyond the Quantum Limit［J］.Nat Photonics，2013，7：229-233.

［4］ Treps N，Andersen U，Buchler B，et al.Surpassing the Standard Quantum Limit for Optical Imaging Using Nonclassical Multimode Light［J］.Phys Rev Lett，2002，88（20）：203601.

［5］ Treps N，Grosse N，Bowen W P，et al.A Quantum Laser Pointer［J］.Science，2003，301：940-943.

［6］ Delaubert V，Treps N，Lassen M，et al.TEM10Homodyne Detection as an Optimal Small-displacement and Tilt-measurement Scheme［J］.Phys Rev A，2006，74：053823.

［7］ Lassen M，Delaubert V，Harb C C，et al.Generation of Squeezing in Higher Order Hermite-Gaussian Modes with an Optical Parametric Amplifier［J］.Journal of European Optical Society，2006，1：06003.

［8］ Novotny L，Sánchez E，Xie X S.Near-field Optical Imaging Using Metal Tips Illuminated by Higer-order Hermite-Gaussian Beams［J］.Ultramicroscopy，1998，71：21-29.

［9］ Du J，Li W，Wen R，Li G，et al.Precision Measurement of Single Atoms Strongly Coupled to the Higher-order Transverse Modes of a High-finesse Optical Cavity［J］.Appl Phys Lett，2013，103：083117.

［10］ Magnus T L Hsu，Vincent Delaubert，Ping Koy Lam，et al Optimal Optical Measurement of Small Displacements［J］.Opt.B：Quantum Semiclass Opt，2004，6：495-501.

［11］ 李睿，翟泽辉，赵姝瑾，等.平衡零拍平移测量实验研究［J］.物理学报，2010，59（11）：7724-05.

［12］ Helstrom C.The Minimum Variance of Estimates in Quantum Signal Detection ［J］.IEEE Trans Inf Theory，1968，IT14（2）：234-242.

［13］ Treps N，Delaubert V，Maître A，et al.Quantum Noise in Multipixel Image Processing ［J］.Phys Rev A，2005，71：013820.