Excel在本科概率统计教学中的应用

陈永娟

(莆田学院数学学院，福建 莆田 351100)

在本科阶段概率论与数理统计这门课是大多数专业的一门基础课。它是一门生动有趣实用性很强的课程，但是如果只讲授理论，忽视应用，那将使得这门课索然无味。因此，必须找到一种软件能够实现其理论。专业的概率统计软件有SPSS、SAS、Statistica等，但是它们的系统庞大、结构复杂。处理本科阶段的概率统计的相关问题时，并不需要这么强的软件。从可获得性，可操作性来讲，Excel软件是最适合本科概率统计教学使用的。Excel中的统计函数和数据分析工具和VBA几乎可以解决本科概率统计教学中遇到的所有的相关问题，而且易学，便于掌握。学生们能够通过软件很快实现课堂上老师所授予的知识，大大地提高他们的学习兴趣，从而能够达到本课程的教学目的。但在实际的授课中，有很多教师只把软件的应用看成可选的，没有要求必须要掌握，在大纲中也没有体现相关内容，考试也大部分不用考查。这就导致学生也不够重视，这是很遗憾的。国外的一些概统计教材的编写和教学上对于软件的传授上是很值得学习的［1］。本文根据本科阶段这门课所包含的基本内容举几个典型的例子，阐述在教学中积极地使用Excel软件能取得更好的教学效果。

1 概率的计算

在概率论的教学中，会遇到一些复杂的计算无法直接计算，教师在课堂上通常会直接给出答案。如果教师能够通过软件演示计算过程，这将激发学生的学习兴趣。事实上这样做并不困难，下面举个例子。

例1 已知某一大批产品的一级品率为0.2，现在从中随机地抽查100只，(1)100只元件恰有20只为一级品的概率是多少?(2)至少有20只为一级品的概率是多少?

解:设X表示100只产品中一级品的个数，则 X ～ b(k;100，0.2)

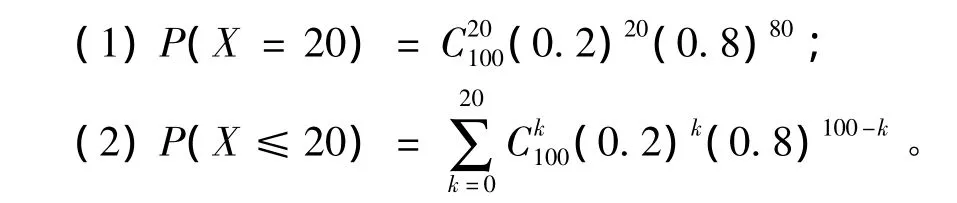
直接计算以上两个概率很困难，但只要使用Excel中的统计函数提供的二项分布的函数，就很容易计算出来。

其格式如下:BINOM.DIST(number_s，trials，probability_s，cumulative)，它返回二项分布的概率值。Numbers为k的值，trials为试验次数n的值;probabilitys为p的值，culmulative是个逻辑值，若为FALSE，返回为概率函数，若为TRUE，返回概率分布函数。计算P(X=20)只需在单元格中输入 “=BINOM. DIST(20，100，0.2，FALSE)”，然后回车结果为0.0993。计算P(X≤20)，只需在单元格中输入“=BINOM.DIST(20，100，0.2，TRUE)”，回车，结果为0.5595。

Excel还提供了其它分布的函数，常见的有泊松分布POISSON.DIST，正态分布函数 NORM.DIST，t分布函数T.DIST等。利用这些函数计算时，跟二项分布类似，只要将相应的参数和逻辑值输入即可得到所需要的答案［2］。

2 定理的模拟

概率论中有些定理比较抽象，但是能够通过模拟阐述定理内容那就生动有趣多了。

2.1 泊松定理的模拟

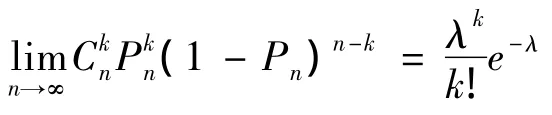
对于这个定理的简单模拟，只要用到Excel中的二项分布函数BINOM.DIST和泊松分布函数POISSON.DIST即可。

如图1所示，考虑一个p=0.02的二项分布概率模型。在C2单元格输入试验次数100，在D2单元格输入“=BINOM.DIST(20，C2，0.02，FALSE)”，得到相应的二项分布的概率;在E2单元格输入“=POISSON.DIST(20，C2*0.02，FALSE)”，得到参数为0.02n的泊松分布的概率。在F2单元格输入“=E2/D2”，得到泊松分布概率与二项分布的概率的比值。只要将填充柄往下拉即可得到其他试验次数对应的值。插入图表，横轴指向 C列(试验次数)，纵轴指向F列(两个分布概率的比值)。从图上可以看出当试验次数充分大时，泊松分布与二项分布概率的比值趋向于1，即二项分布b(k;n，p)近似服从参数为np的泊松分布。

图1 泊松定理的模拟

2.2 贝努里大数定律的模拟

贝努里大数定律表明，在大样本条件下，事件发生的频率依概率收敛于事件发生的概率。

下面采用Excel中VBA开发工具和一些简单的辅助工具实现贝努里大数定律的模拟。通过VBA编写的简单程序，运行界面如图2所示，图中设置有一个按钮“CommandButton1”，它与VBA过程代码相关联，点击即可运行VBA过程 。在VBA内有个“Rnd”函数是一个随机发生器，它产生 (0，1)区间上均匀分布的随机数。设这个随机数为 R，设 X=，则 X 服从参数为 p 的(0－1)分布。令事件A={X=1}，由均匀分布性质，P(A)=P(X=1)=P(R≤p)=p。则有如图2所示，在“D2”单元格中输入试验次数为2000，在“E2”中输入概率值p为0.5，工作表的A列为试验次数，B列为每次试验事件A是否发生(即X的取值，事件A发生取1，不发生取0，通过VBA简单编程实现)，C列为事件A发生的频率。在表中插入的图表横轴指向A列 (事件A发生的次数)，纵轴指向C列 (事件A发生的频率)，从图中可以看出当试验次数趋向2000时，事件A发生的频率较好地收敛于事件A发生的概率p=0.5［3］。

图2 贝努里大数定律的模拟

3 灵活使用Excel解决统计学教学中的问题

Excel中提供了很多工具，可以解决数理统计中的问题。如假设检验，方差分析和一元线归回归等。文献 ［4］的第十一章较详细地介绍了Excel软件在数理统计中的应用。有些问题可以直接通过Excel分析工具，如双样本的 t检验，F检验等。有些问题Excel并不提供直接的分析工具，但可以通过简单函数来解决相关问题，如单样本方差假设的t检验。下面举个简单的例子。

例2 某元件的寿命X服从正态分布N(μ，σ2)，μ，σ2均未知，现测量16只元件的寿命如下:

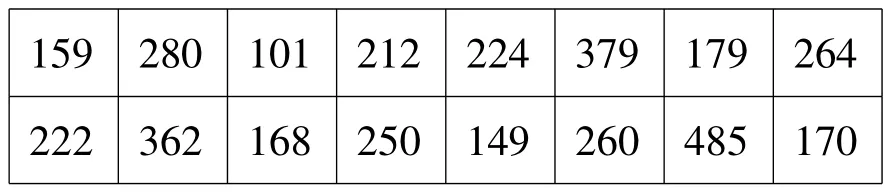
159 280 101 212 224 379 179 264 222 362 168 250 149 260 485 170

解:按题意需要检验:H0:μ≤μ0=225，H1::μ＞225

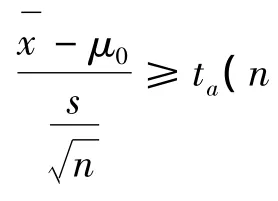
具体操作如下:

1)在Excle界面，将样本数据输到A1:A16;

2)在C2单元格输入“=AVERAGE(A1:A16)”，回车得x=241.5;

3)在C3单元格输入“=STDEVA(A1:A16)”，回车得s=98.72588;

4)在C5单元格输入“=(C2－225)/(C3/SQRT(16))”，回车得t0=0.668513;

5)在 C7单元格输入“=T.INV(0.05，15)”，回车得－1.75305，T.INV函数返回的是t分布的左尾区间值，所以由t分布的对称性可知，t0.05(15)=1.75305［4］。

图3 实现结果 (例2)

由t0=0.668513＜1.75305，可知，t没有落入拒绝域，故接受H0，即认为元件的平均寿命不大于225。

4 结束语

从应用Excel处理本科阶段概率统计教学中的问题的实例可以看出，只要弄通、吃透教材，明确教学目的和重点难点，合理地运用Excel所提供的工具，就可以很好地解决本科阶段概率统计教学中的复杂计算、数据处理、定理模拟等相关问题。采用Excel软件来进行教学，可以激发学生的学习兴趣，使学生容易进入和保持学习的积极状态，从而大大提高了教学效率。

［1］德沃尔.海外优秀数学教材系列丛书:概率论与数理统计［M］.北京:高等教育出版社，2004:52－158

［2］刘亦斌.利用Excel的统计函数进行概率运算［J］.宜春学院学报，2008，28(4):11 －14

［3］韦程东.从大数定律随机模拟谈Excel在概率论与数理统计教学中的应用［J］.广西民族学院学报(自然科学版)，2002，8(4):60 －67

［4］盛骤等.概率论与数理统计(第四版)［M］.北京:高等教育出版社，2008:183－184