N沟道VDMOS器件材料选择

盖锡民，王震宇

(丹东安顺微电子有限公司，辽宁 丹东 118002)

VDMOSFET属于功率MOSFET，简称VDMOS。这种器件采用电压控制方式，其特点是具有很高的输入阻抗，良好的热稳定性以及很高的开关速度，因而得到了日益广泛地应用。在VDMOS器件制程中硅外延材料的选择是制程中的第一步，也是十分重要的一步。由于是N沟道器件，选择N(100)晶向的材料是十分必要的，它的表面的界面态密度较低［1］，所以几乎所有的MOS器件都选择这一晶向，对于非穿通型VDMOS器件而言，材料的另外两个参数为外延层的电阻率ρ和外延层的厚度We如何选择就成为问题的关键。

在满足VDMOS器件的耐压BVDS中起决定作用的是材料外延层的电阻率ρ。外延层的电阻率ρ越大，器件的耐压值BVDS越高。如果外延层的电阻率选择过大，虽然器件的耐压值BVDS得到了充分的满足，但VDMOS器件的导通电阻Ron也将变大，而VDMOS器件所期望的是在满足耐压BVDS的同时，导通电阻 Ron越小越好［5－6］，这就需要对特定参数的VDMOS器件，在制作时所选取的电阻率要恰到好处，在满足耐压BVDS的同时，电阻率不要过高。如果电阻率值选取太低，虽然导通电阻Ron较小，但耐压BVDS就不能满足器件的要求。

对于外延层厚度We的选择，非穿通型VDMOS器件We要满足P－区的纵向结深Xjp，最大反向耐压时PN结的空间电荷区宽度Xmn，以及重掺杂衬底向外延区的自掺杂厚度Hf三者之和，在此基础上稍有余量即可。如果We选择太小，将会使VDMOS器件变成穿通型器件，耐压值变低;We选择太大，同样会使器件的导通电阻Ron变大。

通常VDMOS器件中耐压和电流值是非常重要的两个参数，市场上在不同用途情况下VDMOS器件的这两个参数的要求是多种多样的，任何一家公司的产品都不可能包罗万象，生产所有参数款项的产品。因而在市场对某一特定参数的产品的需求量上升时，各家公司都会争先恐后开发试样，在样品试制过程中重要的是缩短试制流程，及时占领市场。如果选择材料不当，会使样品无法满足市场要求，形成多次选择，多次试样，延长提供样品的时间，失去宝贵的市场先机，这直接有损企业的效益。因此，如何能够快速准确的选择材料，其意义十分巨大。

1 VDMOS器件材料外延层电阻率和厚度的理论计算

图1 N沟道VDMOS器件纵向示意图

对于VDMOS器件，如何获得足够高的耐压和非常低的导通电阻Ron是设计中必须同时考虑的两个重要问题。导通电阻Ron主要由外延层电阻决定。外延层越厚，以及电阻率越高，器件耐压也越高，同时导通电阻Ron也越大。因此，对于VDMOS器件存在耐压与导通电阻的矛盾，两者都主要取决于外延区参数 (厚度和掺杂浓度)。下面以60V耐压的VDMOS器件为例，用理论计算的方法确定材料外延层的电阻率和厚度。

1.1 外延层电阻率的理论计算

外延层的电阻率的大小取决于外延层的掺杂浓度，掺杂浓度越小其电阻率越大。理想情况下外延层掺杂浓度为［2］:

BVDS由器件指标给出，为60V，带入上式得外延层的掺杂浓度为:

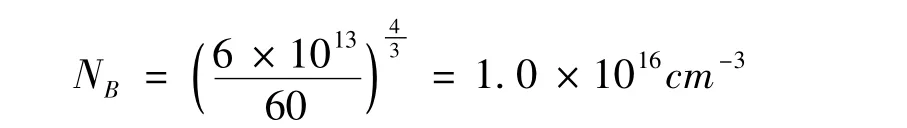
而外延层的掺杂浓度与外延层的电阻率关系为［2］:

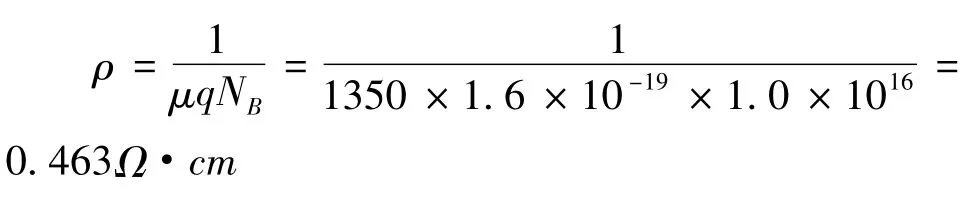
上式中μ为本征硅的电子迁移率，其值为1350 cm2/V·s，q为电子电荷的电量，其值为1.6×10－19C，ρ为电阻率。

1.2 外延层厚度的理论计算

1.2.1 P区掺杂浓度的确定

P－区掺杂浓度Na和栅氧化层的厚度tox决定了器件的阈值电压VT，但Na还受器件沟道穿通电压的限制，所以应先从满足耐压的角度确定出Na的值，然后再按给定的阈值电压的值求出tox.

如果从满足耐压的角度来考虑P区掺杂浓度Na可以稍大一点，但这个值与栅氧化层厚度tox一起受阈值电压的约束，也并不是没有条件的越大越好，阈值电压［2］可近似表示为

上式中，QB为耗尽层电荷，不同工艺条件QOX不同，QOX完全由工艺条件决定，工艺操作以及过程如果不同将会使QOX不同，通常可以取QOX=8 ×10－8C;COX= ε0εOX/tOX是单位面积栅氧化层电容;φSS功函数差，可表示为φSS=0.026V·ln(NaNd/ni2)。Nd是多晶硅的掺杂浓度，通常可以取值为8×1018个/cm3。对于低压或高压 VDMOS器件，φf值的范围在0.40～0.45变化不大，在这里可以取φf=0.43。

根据上式 (1－2)并利用牛顿迭代法计算在一定的阈值电压下，tox和Na的对应关系如表1所示，取VT=3.1V。

表1 栅氧化层厚度与P区掺杂浓度的关系表

因为氧化层越厚则器件的频率特性约好，氧化层厚度应该尽量取厚一些，但氧化层太厚会使器件的特征导通电阻变大，两者之间存在着相互制约的矛盾。根据给定的阈值电压指标，经过综合考虑后，取氧化层厚度为450埃，即tox=450A。则根据表1可以求得Na=3.43×1017atom/cm3。

1.2.2 外延层厚度的计算

如图1所示的那样，外延层厚度We应为

上式中，xmn为PN－结在N－侧的空间电荷区宽度，即为电子漂移区的扩展宽度;Hf为器件在制造过程中经历的高温过程中，N+衬底向N－外延区反扩的深度，即自掺杂的结深。在这三部分当中，xmn可以通过电参数值进行计算［2］，

上式中ε0为自由空间电容率，其值为8.854×10－14F/cm，εs半导体介电常数，其值为11.9，将参数指标的耐压60V代入式 (1－3)，即可求出PN－结在N－侧的空间电荷区宽度，xmn=2.8um。

在VDMOS器件中，xjp是设计中必须准确给出的量。P区和N+区横向结深差形成沟道，沟道长度L是决定功率器件电流性能的决定部分，因此，必须正确设计各区结深。由于在掺杂的时候，横向结深是纵向结深的0.85倍，所以沟道长度L为［2］

式中xjn为以工艺稳定为前提的N型最小结深，因为xjn越小，特征电阻越小。一般采用砷注入的0.4um工艺。由于采用的是自对准工艺，沟道长L由P区掺杂浓度Na及其退火工艺决定。同样由式(1－2)计算当PN结加反向电压时，在高掺杂P侧耗尽的宽度 xmp为［2］:

代入数值后，求得xmp=0.48um时，为了防止沟道穿通，沟道长度必须大于这个耗尽层宽度，即L必须大于0.48um，为了留出充分的余量，取L=0.7um。代入式 (1－6)得:

在式 (1－3)中的Hf由工艺温度和高温时间所决定，对于60V的工艺取Hf=1.5um。则由 (1－3)式可以求得外延层厚度We=5.6um。

2 外延层电阻率和厚度的理论计算结果的修正

在材料选择上，一般有两种方式:一种是完全根据理论计算获得材料的外延层的电阻率和厚度，另一种则是根据经验来确定，但往往两者都无法快速准确地满足实际生产中需求，这就需要相对精确地将二者和谐统一起来，即理论与实践有效地相结合。

如果简单地采用上述理论计算所获得的材料的外延电阻率ρ=0.463Ω·cm，外延层厚度We=5.6um，就会发现所制成的VDMOS器件的耐压值只能达到30V左右，与设计要求的60V有非常大的差距，说明理论值与实际值存在较大的误差。所以必须对误差产生的原因进行分析，并对理论计算的结果进行相应地修正。

2.1 外延层电阻率的修正

外延层电阻率值理论计算的结果ρ=0.463Ω·cm，是指所有的条件都处在理想条件下器件才能达到耐压值60V，实际上制约VDMOS器件耐压值的因素很多，如氧化层内可动电荷数量会对器件的耐压值产生较大的影响［1］，尽管采取控制措施，氧化层内仍会存在相当数量的可动电荷使器件的耐压值变低。还有一个重要因素是P－区的结深也会直接影响VDMOS器件的耐压值BVDS。为了减小器件的导通电阻提高开关速度，P－区的结深控制在1 um ～2 um之间，而较薄的P－区会使结面的弯曲部分的曲率半径较小，从而使器件的耐压值变低［3］。尽管在器件的设计上采取了加场板和分压环等措施，但实际耐压还是与理论值相差较大。实际采用的电阻率应在理论值的基础上乘以一个修正因子K，对于耐压值低于200V的VDMOS器件，K值一般在2～3左右。所以上述电阻率的实际值应选范围为:K·ρ≈0.9 Ω·cm ～1.4 Ω·cm。考虑到外延掺杂时，由于设备和工艺的限制，电阻率存在±5%左右的误差，综合考虑，修正以后的电阻率选在1.2±5% Ω·cm。

2.2 外延层厚度的修正

外延层值理论计算的结果We=5.6um，也是指所有条件都在理想情况下所需选取的值。对外延层厚度的修正要考虑以下几个因素，一是P－区结深的工艺波动，其幅度一般小于10%，二是自掺杂的厚度Hf，它跟工艺的所有高温过程密切相关，目前衬底N+区都采用重掺砷材料，因为砷的扩散系数较小，所以自掺杂的波动幅度也不大，一般小于10%。另外外延制做过程中，厚度的控制范围在±5%左右，以上因素综合考虑并留取一定余量，外延厚度的选值为:We=7.5±5%um。

3 结束语

对于微电子产品的开发和设计人员，准确地选取材料永远都是重要的课题。以N沟道VDMOS器件为例，以耐压60V为例，不过是以点带面地去进行理论的和实际的探究，藉此抛砖引玉而已。延伸开来，相较于60V的VDMOS器件，具有更低耐压和更高耐压的VDMOS器件，其工艺特点各不相同，比如说基于成本的考虑更小的耐压不会设计较多的分压环，而较高的耐压在场板设计和分压环的设计上则会下些功夫，工艺上也有许多差别，最终在材料的选取上体现在电阻率的修正因子K值则各不相同。一般来说，更低耐压的VDMOS器件K值选择大于3，更高耐压的K值则在1～2左右。而外延层厚度的选取，相较于理论值的偏差则更多的取决于工艺上的过程。当满足了耐压条件之后，为了获得较低的导通电阻，则必须选择最低的电阻率和最薄的外延厚度。

［1］郭维廉.硅－二氧化硅界面物理［M］.北京:国防工业出版社，1984

［2］曹培栋.微电子技术基础—双极、场效应晶体管原理［M］.北京:电子工业出版社，2001

［3］施敏.半导体器件物理［M］.北京:电子工业出版社，1987

［4］张华曹，涂序梅.VDMOS击穿电压与导通电阻的最佳设计［J］.陕西机械学院学报，1992，(1):27－33

［5］高雅君.VDMOSFET导通电阻的最佳化设计［J］.飞机设计，2002，(2):48 －51

［6］赵野，张颖，高嵩，等.低压VDMOSFET导通电阻的优化设计［J］.辽宁大学学报(自然科学版)，2001，28(3):247－252