An Approximate Gradient Algorithm for Constrained Distributed Convex Optimization

Yanqiong ZhangYoucheng LouYiguang Hong

I.INTRODUCTION

RECENT years have witnessed increasing research interests concerning the collective dynamics and distributed control in a variety of scenarios,including consensus, flocking and distributed optimization[1−8].In fact,distributed multiagent optimization of a sum of convex functions has become a hot topic with various applications in sensor network,source localization,and robust estimation[9−12].

The current literature offers a large body of work on designing discrete-time algorithms to find a solution of the distributed optimization problem,including the subgradient-based incremental methods with deterministic or randomized iteration,where each agent is able to compute a local subgradient of its own objective function[11−14].In addition,there are many nonsubgradient-based methods.For instance,Gossip algorithms were developed to solve unconstrained optimization problems in[15−16].Moreover,an augmented Lagrangian method was proposed in[17].

In this study,we consider a multi-agent convex optimization problem,whose goal is to minimize the sum of local objective functions,subject to a global constraint.This problem is motivated by those in distributed source localization,network utility maximization,optimal flow control in power systems and so on[18−20].A recent paper[21]studied the problem by proposing two distributed primal-dual subgradient algorithms.These algorithms are based on the characterization of the primal-dual optimal solutions as the saddle points of the Lagrangian(penalty)functions.From the optimization theory,we know that a vectordcan be selected as a feasible descent direction of differentiable functionfif it satisfies〈d,▽f〉＜0.Clearly,antigradient−▽fis one of the feasible descent directions.However,in practical applications,it may be hard to obtain the exact gradient which,however can be computed approximately.Therefore,we propose an approximate gradient algorithm in this paper.The communication graph is assumed to be directed,switching,periodically strongly connected;we prove that the multi-agent system can achieve a global optimal consensus with some approximate gradient accuracy conditions.

This paper is organized as follows.In Section II,we introduce concepts and preliminary results in graph theory and convex analysis along with the formulation of the constrained distributed optimization problem under investigation.Then the approximate gradient algorithm is provided in Section III.The main results and convergence analysis are obtained for the considered algorithm in Section IV.Simulation results are provided in Section V.Finally,concluding remarks are made in Section VI.

II.PRELIMINARY

In this section,we review some useful related concepts in algebraic graph theory[22]and convex analysis[23],and then formulate the constrained distributed optimization problem under investigation.

A.Graph Theory and Convex Analysis

A directed graph is a pair,G=(V,E),whereV={1,2,···,N}is the node set andE⊆V×Vis the edge set.Nodeiis a neighbor ofjif(i,j)∈Eand we useNito denote the set of neighbors of nodei.A path of lengthrfrom nodei1to nodeir+1is a sequence ofr+1 distinct nodesi1,···,ir+1such that(iq,iq+1)∈Eforq=1,···,r.If there is a path between any two nodes(i,j∈V),thenGis said to be strongly connected.

A setQ⊆Rnis convex ifax+(1−a)y∈Qfor anyx,y∈Qand 0≤a≤1.For anyx∈Rn,there is a unique elementPQ[x]∈Qsatisfying‖x−PQ[x]‖=infy∈Q‖x−y‖,which is denoted by|x|Q,whereQ⊆Rnis a closed convex set,PQdenotes the projection operator ontoQand‖·‖is the 2-norm in the Euclidean space.A functionf(·):Rn→R is said to be convex iff(ax+(1−a)y)≤af(x)+(1−a)f(y)for anyx,y∈Rnand 0≤a≤1.Functionfis concave if−fis convex.Vectorξ∈Rnis said to be a subgradient of convex functionfaty∈Rnif the first-order condition of convexity holds:

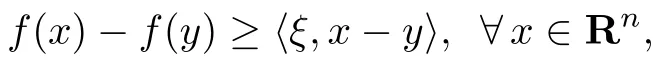
where〈·,·〉denotes the Euclidean inner product.The set of all subgradients of functionfatyis denoted as∂f(y).FunctionL:X1×X2→R withX1⊆RnandX2⊆Rmbeing closed and convex,is convex-concave if it is convex on its being first argument and concave on the second one.Pointis a saddle point ofLoverX1×X2if.

B.Problem Formulation

Consider a network composed of agentsV={1,···,N}that can only interact with each other through local communication.The objective of the multi-agent system is to cooperatively solve the following optimization problem:

wherefi:Rn→R is the convex differentiable objective function of agenti,xis a global decision vector andXis the compact and convex global constraint set.As usual,we assume thatfiis only known by agentiand the functiong:Rn→Rmis convex and known to all the agents.Denote

In this paper,we assume the feasible setYis nonempty.According to the compactness ofYwith Weierstrass′theorem,the optimal solution setX∗of problem(1)is nonempty and the optimal valuep∗is finite.The following Slater′s condition is important in our analysis.

Assumption 1.There exists a vector,,such that＜0.

The communication over the multi-agent system at timek≥0 can be described by a directed graphGk=(V,E(k)),whereE(k)⊆V×Vrepresents the set of communication links at timek.For any two agentsi,j∈V,jcan get the information fromiat timekif and only if(i,j)∈E(k).Letaij(k)represent the weight of edge(j,i)at timek,with the property thataij(k)＞0 if(j,i)∈E(k),andaij(k)=0,otherwise.In this paper,we assume(i,i)∈E(k)for alliandk.The following two assumptions on the interconnection graphs for the multi-agent network are widely used in the optimization computation[4,11−12].

Assumption 2(Weight rule).There is 0＜η＜1 such that,for alli,j∈Vandk≥0,aii(k)≥ηandaij≥ηif.Moreover,.

Assumption 3(Connectivity).There is a positive integerBsuch that the directed graphis strongly connected fork≥0.

C.Approximate Gradient

Sub-gradient methods have been widely used to solve the distributed optimization problems[11−12,21].From the optimization theory,we know that vectordcan be selected as a feasible descent direction of differentiable functionhif〈d,▽h〉＜0.Obviously,−▽his one of the feasible descent directions.However in some practical applications,the exact gradient is hard to obtain but can be computed approximately.

Next,we give the definition of approximate gradient.

Definition 1.For anyz,denote▽h(z)the exact gradient of differentiable functionhatz.By defining setsthe approximate gradient▽ha(z,θ)of pointzwith approximate angleθis defined as the following set:

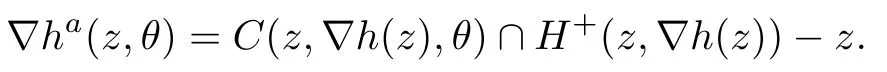
In fact,C(z,▽h(z),θ)−zis a convex cone generated by all vectors having angles with▽h(z)no greater thanθ,andH+(z,▽h(z))is a closed half-space(see Fig.1 for illustration).

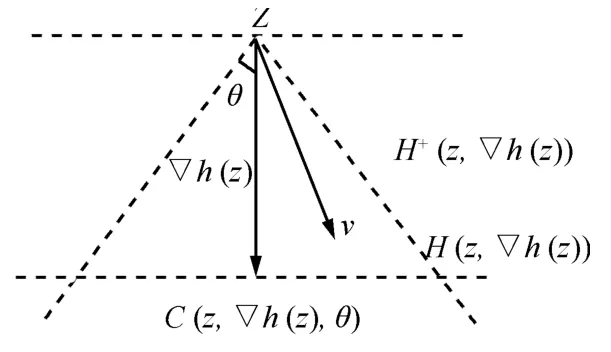
Fig.1.Illustration of the approximate gradient.

Define

Then the supporting approximate gradient▽hsa(z,θ)of pointzwith approximate angleθis defined as the following set:

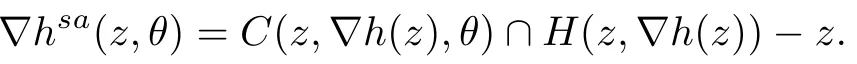
According to Definition 1,for anyda∈▽ha(z,θ),we can associatedsawithdsa∈▽hsa(z,θ)such that

for some 0≤ζ≤1,whereζis termed as norm relaxation.

III.APPROXIMATE GRADIENT ALGORITHM

In this section,we propose the approximate gradient algorithm for distributed convex optimization.This algorithm can be reduced to the“distributed penalty primal-dual subgradient algorithm”given in[21]when the approximate angle is zero and norm relaxation is equal to one.

At first,problem(1)is equivalent to

The dual penalty problem is defined by

The dual penalty objective functionis defined byq(λ)=infx∈XL(x,λ),whereL(x,λ):Rn×Rm≥0→R is expressed as with.DenoteD∗as the set of optimal points of the dual penalty problem(3)andq∗as the optimal value.

The Slater′s condition can ensure the zero duality gap(that is,p∗=q∗)and the existence of the optimal solutions of the dual penalty problem(3)(that is,D∗/=∅).In addition,(x∗,λ∗)∈X∗×D∗if and only if it is a saddle point of the Lagrange penalty functionL(x,λ)under Slater′s condition(see[21,23]for the references therein).Let

which can be viewed as the Lagrange penalty function of agenti.In this way,we haveandLi(x,λ)is convex inxand concave(actually,linear)inλ.

The approximate gradient algorithm is described as follows:

whereαkis the step size at timek,=and

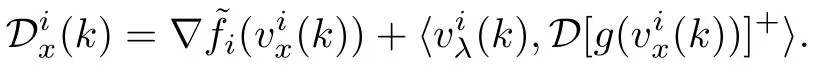
Here,is the approximate gradient of the accurate gradient direction,θikis the approximate angle andis a subgradient ofat.

According to the definition of supporting approximate gradient,there existδik∈[0,1]and∈such that

Letand.For the approximate angleθik,step-sizeαkand norm relaxationδik,we make the following assumptions:

Assumption 4(Approximate angle).For everyi∈V,0≤θik≤θ∗＜π/2,∀k.

Assumption 5(Step-sizes).PP,PP.

Remark 1.In fact,the step-size and approximate angle conditions can be satis fied easily in various situations.For instance,,i∈V,k≥0.

IV.CONVERGENCE ANALYSIS

In this section,we establish some basic relations for the sequences{xi(k)}and{λi(k)}obtained by the approximate gradient algorithm(4).

At first,we introduce a useful lemma in[24].

Lemma 1.Letandbe two non-negative sequences withP.Ifak+1≤ak+bk,∀k≥0,then limk→∞akis a finite number.

Next,we give the analysis for the proposed approximate gradient algorithm.

For anyx∈X,by using the standard non-expansiveness property,it follows from(4)that

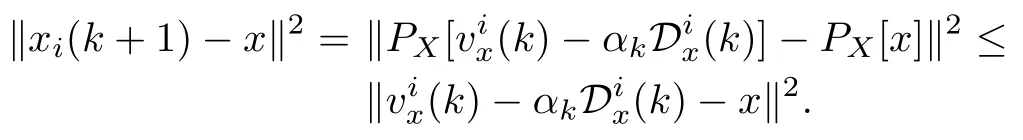
Let〉and.Due to the compactness ofX,we have

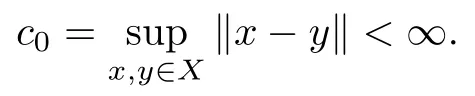
Moreover,it follows from the continuity offiandthat for anyx∈X,there existsL＞0 such that,and,i=1,···,N.From(4),we have,then,which implies,and.Denote,and then+tanθ∗).Moreover,we obtain

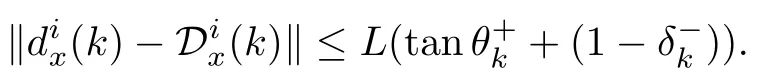
Then we get

With a similar analysis,for any,

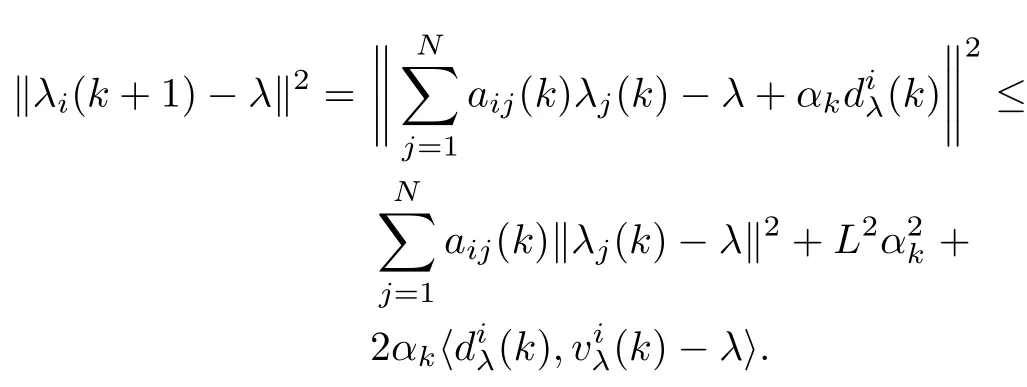
Based on the first-order convexity condition,it follows that

and

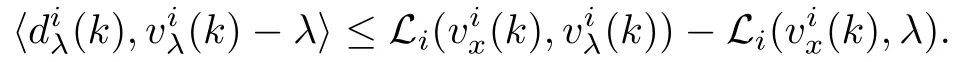
Therefore,we have the following results.

Lemma 2.For any,the following inequalities hold:

and

Lemma 3.Letand=If Assumptions 2～5 hold,then we have

1);

2=0,i=1,···,N;

3)P.

Proof.1)Since

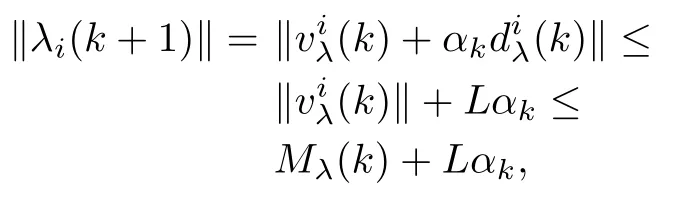
and

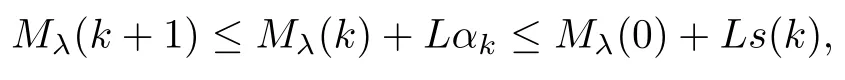
it follows from Assumption 5 that

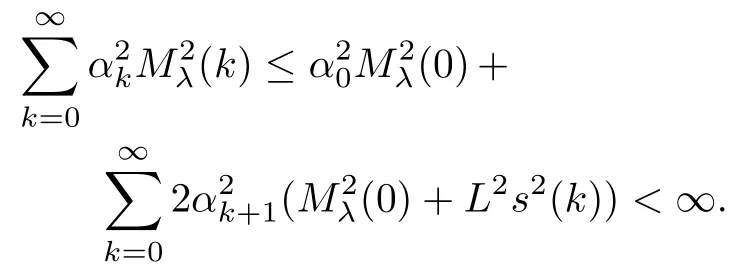
Moreover,limk→∞αkMλ(k)=0.

2)Let Φ(k,s)=A(k)A(k−1)···A(s),whereA(k)=(aij(k)),k≥s.From Proposition 1 in[11],the following result about transition matrices Φ(k,s)holds:

withanddenotes the matrix entry in thei-th row andj-th column.Let.Using the transition matrices and algorithm(4),we have

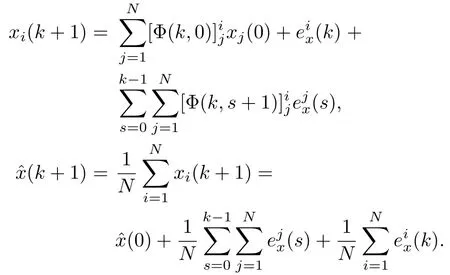
It follows that

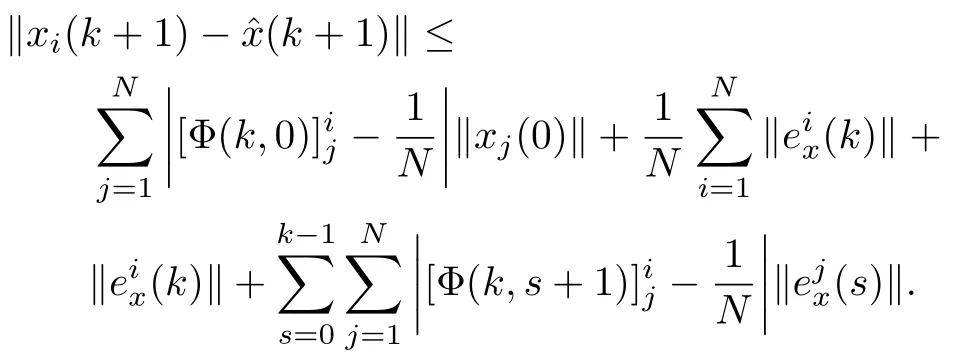
Withand the standard non-expansiveness property of projection operator,we obtain

Recall that.By(7),we have

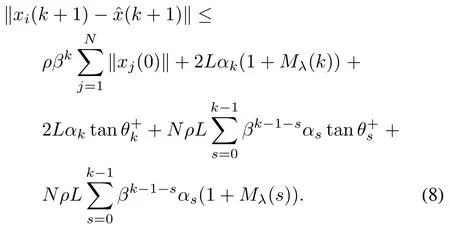
It follows from 0＜β＜1 thatβk→0.Using Lemma 7 in[12],we obtain

3)Multiplying both sides of inequality(8)byαk+1,we have

Using Lemma 7 in[12]again,we obtain

Due to,we have

Following the same technical line,we have

Similar arguments can be employed to show that

□

Lemma 4.Suppose Assumptions 1～5 hold.Let sequences{xi(k)}and{λi(k)}be generated by the algorithm(4).For any(x∗,λ∗)∈X∗×D∗,we have:

1)The limits,limk→∞‖xi(k)−x∗‖and limk→∞‖λi(k)−λ∗‖,are finite for alli∈V;

2)

Proof.1)Let=E(k)+where,,Then we have the following inequalityFor anyx∗∈X∗,it follows from(5)that

where

With a similar analysis,for anyλ∗∈D∗,it follows from(6)that

where

According to Lemma 3 and Assumption 5,we can get PandPCombining(9)and(10),we obtain:

For any(x∗,λ∗)∈X∗×D∗,with Assumption 1,we have that(x∗,λ∗)is a saddle point ofLoverthenand.This implies that

ByLemma1,itfollowsfrom(11)that the limit¡¢exists.Then limitsandalso exist for anyi∈V.

2)Summing the relations(11)overk,we obtain

It can be verified that

Sinceand,we have

and

From(9),we obtain that

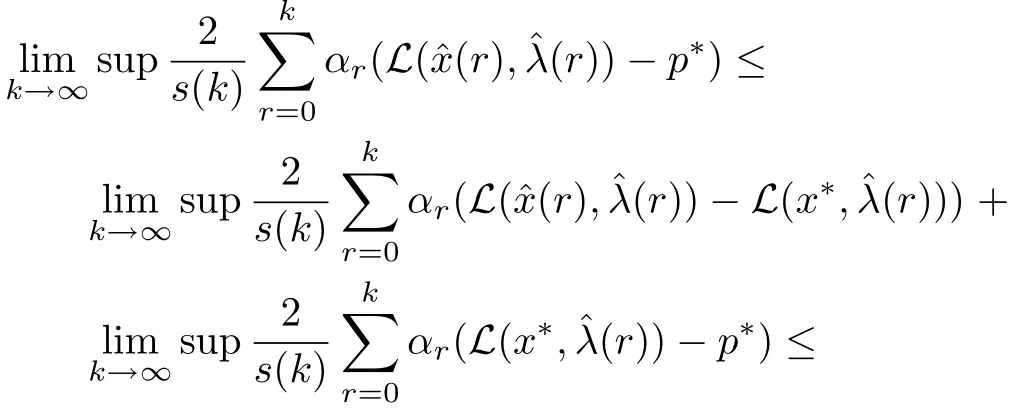
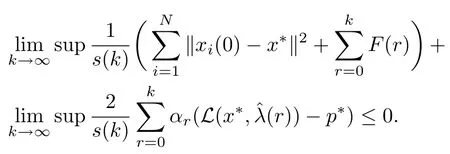
Then we get

With the similar analysis of(10),we can obtain

Hence,.□

Theorem 1.Consider the problem(1),and let the sequence{xi(k)}be generated by the approximate gradient algorithm(4).Under Assumptions 1～5,if the primal optimal setX∗has an interior point,then there exists∗such that

Proof.For any interior pointthere exists an open sphereS1centered atsuch thatS1⊆X∗.For anyx∈S1,from Lemma 4,we have limk→∞‖xi(k)−x‖exists.It can be veri fied that there existssuch that.Following the analogous line to Claim 4 in[21],we can show that∗.Thus,the conclusion follows.□

Remark 2.The main difference between the approximate gradient algorithm in this paper and the algorithm in[21]is that we take the gradient computation errors into account and propose a new approximate algorithm.

V.SIMULATION

In this section,we give simulation results to illustrate the distributed approximate gradient algorithm proposed in this paper.

Example 1.Consider a group of three agents with the switching interaction topologies to cooperatively solve the problem(1).Letg(x,y)=(x−y)2−4,constraint setX=[−2,2]×[−2,2]⊆R2,fi(x,y)=fi(x)+fi(y),i=1,2,3,where

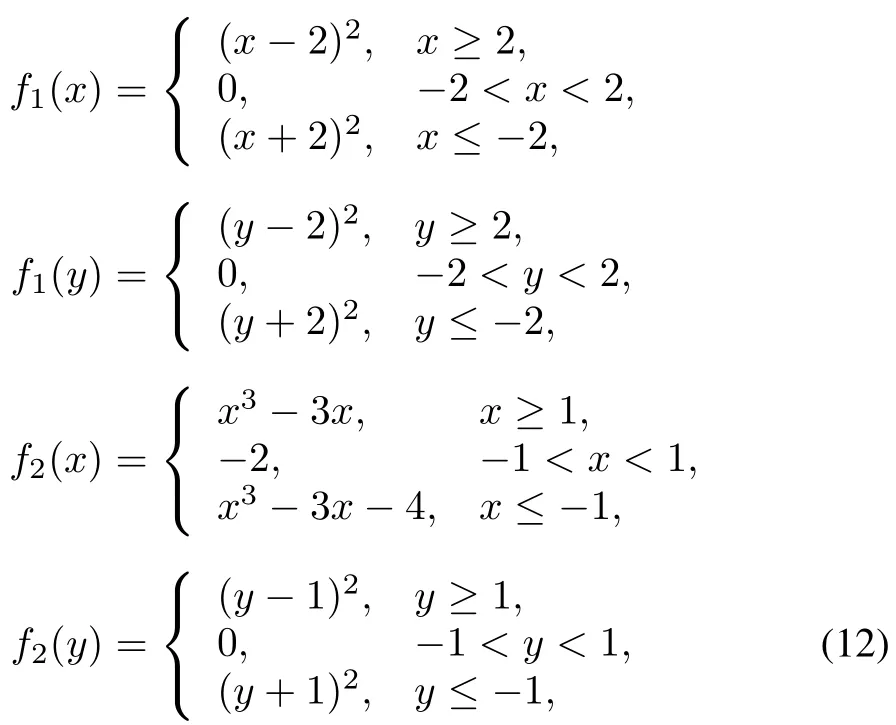
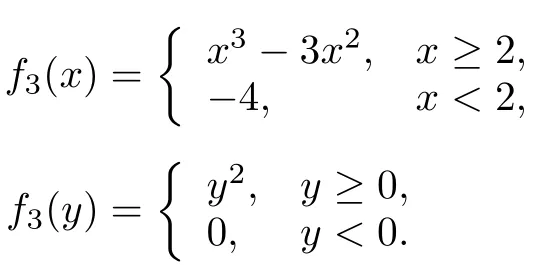
The topologyGis switched between graphsGi,i=1,2,whereG(2k)=G1andG(2k+1)=G2fork=0,1,···.The corresponding adjacency matrices are described byA1andA2:

The convergence processes of algorithm(4)are shown in Fig.2.Here we take step-sizesαk=1/(k+2),norm relaxationδik=(k+1)/(k+2),andνik=1/(k+2),whereνikis the angle between the exact gradient and the approximate gradient for agentiat timek.

Denote(xi(k),yi(k))the estimate of the optimal solution of the problem(1)for agentiat timek.From Fig.2,we can see that all the agents converge to the same optimal point.

VI.CONCLUSIONS

This paper investigated a multi-agent optimization problem where each agent aims to minimize the sum of local objective functions subject to a global inequality constraint and a global constraint set.Based on the distributed subgradient methods,we proposed an approximate gradient algorithm when each agent does not have the exact gradient.The conditions were obtained for the approximate gradient algorithm on how large the gradient errors can be tolerated to ensure the convergence of the proposed algorithm.More generalized and interesting cases on approximate gradient algorithms are still under investigation.

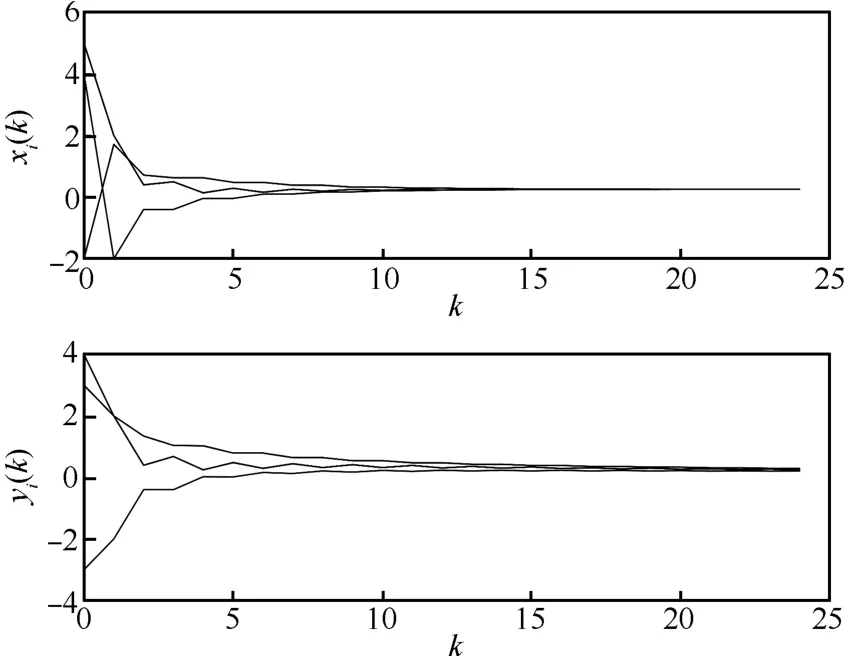
Fig.2.The convergence of approximate gradient algorithm.

REFERENCES

[1]Shi G D,Johansson K H,Hong Y G.Reaching an optimal consensus:dynamical systems that compute intersections of convex sets.IEEE Transactions on Automatic Control,2013,58(3):610−622

[2]Shi G D,Johansson K H.Randomized optimal consensus of multi-agent systems.Automatica,2012,48(12):3018−3033

[3]Lou Y C,Hong Y G.Target containment control of multi-agent systems with random switching interconnection topologies.Automatica,2012,48(5):879−885

[4]Lou Y C,Shi G D,Johansson K H,Hong Y G.Reaching optimal consensus for multi-agent systems based on approximate projection.In:Proceedings of the 10th World Congress on Intelligent Control and Automation(WCICA).Beijing,China:IEEE,2012.2794−2800

[5]Ren W,Beard R.Consensus seeking in multi-agent systems under dynamically changing interaction topologies.IEEE Transactions on Automatic Control,2005,50(5):655−661

[6]Olfati-Saber R.Flocking for multi-agent dynamic systems:algorithms and theory.IEEE Transactions on Automatic Control,2006,51(3):401−420

[7]Tang Y,Hong Y.Hierarchical distributed control design for multi-agent systems using approximate simulation.Acta Automatica Sinica,2013,39(6):868−874

[8]Chen J,Yu M,Dou L,Gan M.A fast averaging synchronization algorithm for clock oscillators in nonlinear dynamical network with arbitrary time-delays.Acta Automatica Sinica,2010,36(6):873−880

[9]Rabbat M,Nowak R.Distributed optimization in sensor networks.In:Proceedings of the 3rd International Symposium on Information Processing of Sensor Networks.Berkeley,CA:IEEE,2004.20−27

[10]Wan P,Lemmon M D.Event-triggered distributed optimization in sensor networks.In:Proceedings of the 2010 International Conference on Information Processing of Sensor Networks.San Francisco,CA:IEEE,2010.49−60

[11]Nedic A,Ozdaglar A.Distributed subgradient methods for multi-agent optimization.IEEE Transactions on Automatic Control,2009,54(1):48−61

[12]Nedic A,Ozdaglar A,Parrilo P A.Constrained consensus and optimization in multi-agent networks.IEEE Transactions on Automatic Control,2010,55(4):922−938

[13]Nedic A,Ozdaglar A.Subgradient methods for saddle-point problems.Journal of Optimization Theory and Applications,2009,142(1):205−228

[14]Johansson B,Rabi M,Johansson M.A randomized incremental subgradient method for distributed optimization in networked systems.SIAM Journal on Control and Optimization,2009,20(3):1157−1170

[15]Lu J,Tang C Y,Regier P R,Bow T D.Gossip algorithms for convex consensus optimization over network.IEEE Transactions on Automatic Control,2011,56(12):2917−2923

[16]Lu J,Regier P R,Tang C Y.Control of distributed convex optimization.In:Proceedings of the 49th IEEE Conference on Decision and Control.Atlanta,GA:IEEE,2010.489−495

[17]Jakovetic D,Xavier J,Moura J M.Cooperative convex optimization in networked systems:augmented Lagrangian algorithm with directed gossip communication.IEEE Transactions on Signal Processing,2011,59(8):3889−3902

[18]Rabbat M,Nowak R.Decentralized source localization and tracking.In:Proceedings of the 2004 IEEE International Conference on Acoustics,Speech,and Signal Processing(ICASSP,2004).Montreal,Que:IEEE,2004.921−924

[19]Kelly F,Maulloo A,Tan D.Rate control for communication networks:shadow prices,proportional fairness and stability.Journal of the Operational Research Society,1998,49(3):237−252

[20]Oliveira A R L,Soares S,Nepomuceno L.Optimal active power dispatch combining network flow and interior point approaches.IEEE Transactions on Power Systems,2003,18(4):1235−1240

[21]Zhu M H,Martinez S.On distributed convex optimization under inequality and equality constraints.IEEE Transactions on Automatic Control,2012,57(1):151−164

[22]Godsil C,Royle G.Algebraic Graph Theory.New York:Springer-Verlag,2001

[23]Bertsekas D P,Nedic A,Ozdaglar A.Convex Analysis and Optimization.Belmont,MA:Anthena Science,2003

[24]Poljak B T.Introduction to Optimization.New York:Optimization Software Inc.,2001