Distributed Control of Nonlinear Uncertain Systems:A Cyclic-small-gain Approach

Tengfei LiuZhongping Jiang

I.INTRODUCTION

DISTRIBUTED control for group coordination of multiagent systems has recently attracted signi ficant attention from the control community;see,for example,[1−4]based on Lyapunov methods,[5]using a passivity approach,[6−11]based on linear algebra and graph theory,and[12−14]using output regulation theory.The main objective of distributed control is to achieve some desired group behavior for multiagent systems by taking advantage of local system information and information exchanges among neighboring systems.Distributed control may find applications in sensor networks[15],vehicle coordination and formation[16−19]and smart power grids[20],to name only a few.One group behavior of wide interest is the agreement property,for which the interested variables of multi-agent systems are steered to a common value.It should be noted that most of the previously published papers focus on linear models.

In this paper,we study robust distributed control of nonlinear multi-agent systems.The objective is to steer the outputs of the agents to a desired agreement value.In our problem setting,each agent can use its own output and the outputs of its neighbors for the local control law design,while only the informed agents can access the desired agreement value.In addition,the agents studied in this paper are in the disturbed strict-feedback form[21]and do not take the identical dynamical model.This makes the distributed control problem in this paper signi ficantly different from the decentralized control problem,in which each decentralized controller often assumes the accurate knowledge of the reference signal and does not take advantage of the available information of neighboring agents;see e.g.,[22].

The main contribution of this paper is to present a cyclicsmall-gain approach to robust distributed controller design for nonlinear multi-agent systems.More precisely,we will use the notions of input-to-state stability(ISS)[23−24]and input-to-output stability(IOS)[25−26]to describe the dynamic interaction between the controlled agents,and use the recently developed cyclic-small-gain theorem to guarantee the convergence of the agents′outputs to the agreement value.The reader is referred to[27−29]for more details on cyclic-small-gain theorems for networks of nonlinear systems,and[25−30]for the original small-gain theorems for interconnections of two nonlinear systems.

The rest of the paper is organized as follows.Section II gives the problem formulation.In Section III,we present a design ingredient based on which the closed-loop multi-agent system can be transformed into a network of IOS subsystems.The main result of the paper is given in Section IV.In Section V,we show the robustness of the proposed distributed control strategy with respect to time-delays and disturbances in information exchange.Section VII contains some concluding remarks.

To make the paper self-contained,we give some notationns and definitions that are commonly used in the paper here.R and R+represent then-dimensional Euclidean space and the set of nonnegative real numbers,respectively.|x|represents the Euclidean norm ofx∈Rn.Foru:R+→Rnand∆⊆R+,‖u‖∆represents esssupt∈∆|u(t)|.To simplify the notations,we denote‖u‖∞=‖u‖[0,∞).A functionα:R+→R+is said to be positive definite ifα(0)=0 andα(s)＞0 fors＞0.A continuous functionα:R+→R+is said to be a classKfunction,denoted byα∈K,if it is strictly increasing andα(0)=0;it is said to be a classK∞function,denoted byα∈K∞,if it is a classKfunction and satisfiesα(s)→∞ass→∞.A continuous functionβ:R+×R+→R+is said to be a classKLfunction,denoted byβ∈KL,if,for each fixedt∈R+,functionβ(·,t)is a classKfunction and,for each fixeds∈R+,functionβ(s,·)is decreasing and limt→∞β(s,t)=0.

II.PROBLEM FORMULATION

In this paper,we study the distributed control problem of a group ofNnonlinear agents,of which agenti(1≤i≤N)is described in the strict-feedback form(see,e.g.,[21]):

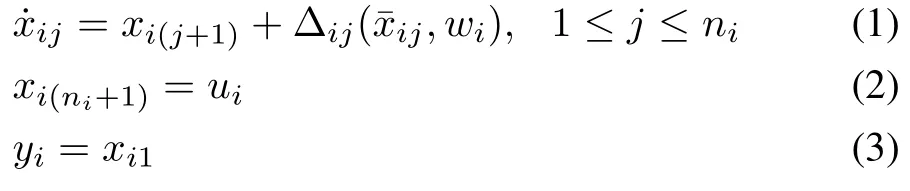
where[xi1,···,xini]T=xi∈Rni,withxij∈R(1≤j≤ni)is the state,ui∈R is the control input,yi∈R is the output,,wi∈Rnwirepresents external disturbances,and∆ij′s(1≤j≤ni)are unknown locally Lipschitz functions.

For distributed control of the multi-agent nonlinear system(1)～(3),we use a directed graph(digraph)Gcto represent the information exchange topology between the agents.DigraphGccontainsNvertices corresponding to theNagents andMdirected edges corresponding to the information exchange links.Speci fically,ifyi−ykis available for local controller design of agenti,then there is a directed link from agentkto agentiand agentkis called a neighbor of agenti;otherwise,there is no link from agentkto agenti.DenoteN={1,···,N}.We useNi⊆Nto represent agenti′s neighbor set.In this paper,an agent is not considered as a neighbor of itself and thusi/∈Nifori∈N.Agentiis called an informed agent if it has access to the knowledge of the agreement valuey0for its local controller design.We useL⊆Nto represent the set of the informed agents.In some works[10,12,14],y0is referred to as a virtual leader.

The objective of this paper is to develop a new class of distributed controllers for the multi-agent system based on the available information such that the outputsyifor 1≤i≤Nconverge to the same desired agreement valuey0.

The following assumption is made on the agreement value and system(1)～(3).

Assumption 1.There exists a nonempty set Ω⊆R such that:

1)y0∈Ω;

2)for each 1≤i≤N,1≤j≤ni,

withaij=[a0,0,···,0]Tfor all,and alla0∈Ω,whereψ∆ij∈K∞is locally Lipschitz and known.

Remark 1.It should be noted that a priori information on the bounds ofy0(and thus Ω)is usually known in practice.In this case,property 2)in Assumption 1 can be guaranteed by application of the mean value theorem.

We also assume the boundedness of the external disturbances.

Assumption 2.For eachi∈N,there exists a constant≥0 such that|wi(t)|≤for allt≥0.

It should be noted that constantis not required to be known.

III.ADESIGN INGREDIENT

The main result in this paper is based on a design ingredient for measurement feedback control of a class of first-order nonlinear uncertain systems.

Consider a nonlinear system

whereξ∈R is the state,ν∈R is the control input,ω∈Rmrepresents the external disturbance,andφ:R×Rm→R is an unknown,locally Lipschitz function.

It is assumed that there exists a known,locally Lipschitzψφ∈K∞such that for allξ,ω,

Here,we do not assume the a priori knowledge ofφ(0,0).

Remark 2.Condition(6)can always be satis fied by a locally Lipschitzφ.Speci fically,one may chooseψφ(s)=max|[ξ,ωT]T|≤s|φ(ξ,ω)−φ(0,0)|+∈swith∈being a positive constant.

The objective of this section is to present a measurement feedback control law by usingξ+δto realize input-to-state stabilization of system(5)withδandωas the inputs.Here,δcan be considered as a measurement error.As shown in the following section,the measurement error in the distributed control of agentiis caused by the unavailability of the accuratey0.Specifically,the desired control law for system(5)is in the form of

whereρandϕare appropriately designed functions andηis the internal state of the control law.

We introduce a dynamic compensator to handle the unknownφ(0,0):

Defineν′=ν+φ(0,0)and.The control problem is solvable if we can design a feedback control law to stabilize the following system withµas the control input:

Sinceφ(0,0)is unknown,ν′is not available for feedback.Note that system(10)and(11)is in the well-known output feedback form[21].In our recent paper[31],we proposed an ISS small-gain approach to measurement output-feedback control of nonlinear uncertain systems in the general output-feedback form by using decentralized observers,and it can be readily applied to the control of system(10)and(11).In[32],this technique has been applied to distributed output-feedback control.It should be noted that the observer designs in[31−32]are originally motivated by[33].Due to space limitation,we directly give the result here without detailed proofs.For system(10)and(11),we can design a measurement output-feedback control law in the form of

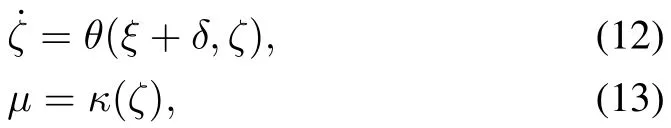
withθandκbeing continuously differentiable functions such that the closed-loop system composed of(10)～(13)is ISS withZ=[ξ,ν′,ζT]Tas the state andδandωas the inputs.Moreover,the closed-loop system is unboundedness observable(UO)and IOS withξas the output.Speci fically,there existαUO,γ,χ∈K,β∈KLand constant,such that for any initial stateZ(0)=Z0and anyδ,ω,

hold for allt≥0.See[25]for the original definitions of UO and IOS.Moreover,the IOS gainγcorresponding toδcan be designed to be arbitrarily close to the identity function Id and the IOS gainχcorresponding toωcan be designed to be arbitrarily small.Here,(12)is designed as the observer to deal with the unavailability ofν′.

Clearly,the control law composed of(9),(12)and(13)is in the form of(1)～(3)withη=[ν,ζT]T.

IV .DISTRIBUTED CONTROL DESIGN

In this section,we show that each agentidefined by(1)～(3)can be recursively designed by using the technique proposed in Section III for system(5).Asy0may not be available to each agent,coordination between the agents is necessary.Thus,the control error of one agent may lead to measurement errors of other agents.The cyclic-small-gain theorem is employed to handle such interconnection between the agents.

In this paper,the local controller for each agentiwill be designed by directly using,defined as follows:

fort≥0,whereNiis the size ofNi.For convenience of discussions,we define

as the difference between the desired agreement signal and the actually available signal.Then,.

The control law for each agentiis in the form of

withrecursively defined as

with eachϕi(j−1)being a continuously differentiable function.

The variablesηi(j−1)forj=2,···,ni+1 are generated by

withρi1andρi(j−1)forj=3,···,ni+1 being continuously differentiable functions and

Note thatIt can be observed that the control law uses the measurements of the known variables,xi1,···,xini.

To prove the effectiveness of the control law above,we consider the dynamics ofei1,···,eini.

By taking the derivative ofei1,we have

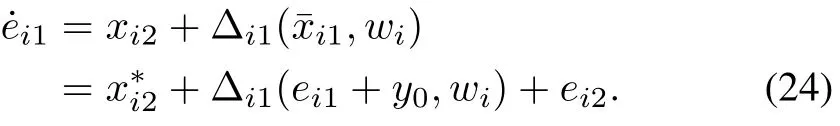
Note thaty0is a constant.By defining=∆i1(ei1+y0,wi)+ei2withtheei1-subsystem can be rewritten in the form of

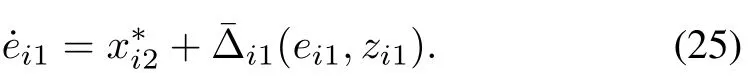
Withei1as the state andas the control input,system(25)is in the form of(5).Note thatei1is not available for feedback.Instead,is available.

Suppose that theei(j−1)-system is in the form of

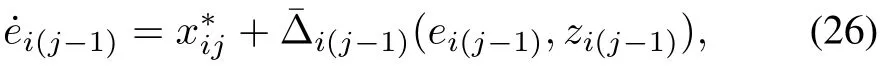
with.Then,withdefined in(23),we have

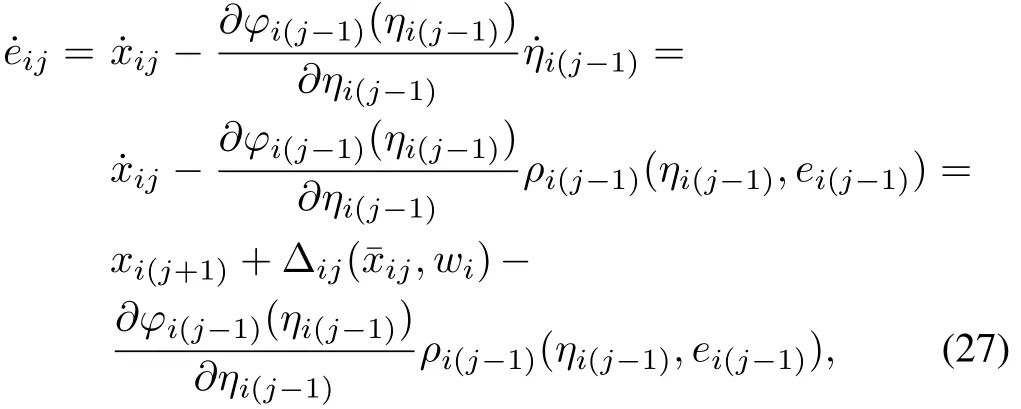
which can be represented by

withThus,forj=1,···,ni,eacheij-subsystem can be rewritten in the form of(28).Note that in the case ofj=ni,ei(j+1)=0.

Under Assumption 1,by using the definitions above,we can directly prove that there exists a known,locally Lipschitzsuch that

Thus,eacheij-subsystem defined by(28)is in the form of(5)and property(29)is in the form of(6).

Now,we study the transformedeij-subsystems and show that the control laws defined by(18)～(23)are the desired ones solving our distributed control problem.With the technique proposed in Section IV,the feedback control law

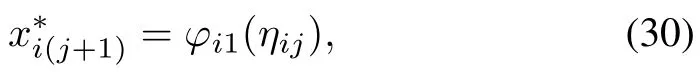
whereηijgenerated by(20)or(21)guarantees that the closed-loop system corresponding to theeij-subsystem is ISS.Moreover,it is UO and IOS withzijas the input andeijas the output.

We give the IOS properties of theei1-subsystem and theeij-subsystems forj=2,···,niseparately:

whereandχij∈Kforj=1,···,ni,andγi1∈K.According to the discussions in Section IV,γi1can be designed to be arbitrarily close to the identity function Id andχijforj=1,···,nican be designed to be arbitrarily small.

Recall the definitions ofdiin(17)andei1in(22).We have

for allt≥0.Note that for any constantsa1,···,an＞0 satisfyingit holds that≤nmax1≤i≤n{aidi}for alld1,···,dn≥0.Thus,we have

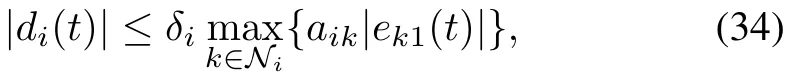
for allt≥0,whereδi=Ni/(Ni+1)ifi∈L,δi=1 ifi/∈L,andaikare positive constants satisfying

Thus,through the distributed control design,the closedloop multi-agent system is transformed into a network of IOS subsystems.We study the condition under which the closed-loop multi-agent system satisfies the cyclic-small-gain condition.We consider two classes of simple cycles in the network:

1)the simple cycles only containing theei1-subsystems;

2)other simple cycles.

Along a simple cycle belonging to the second class,there is at least oneeij-subsystem withj/=1,whose IOS gains can be designed to be arbitrarily small.Thus,the cyclic-smallgain condition can be easily satisfied for the second class of simple cycles.In the following procedure,we propose a condition on the information exchange graphGcto guarantee the satisfaction of the cyclic-small-gain condition for the simple cycles of the first class.

To explicitly study the interconnections between theei1-subsystems,we substitute(34)into property(31).Also,we chooseγi1to be in the form ofγi1(s)=bis,where constantbi＞1 can be designed to be arbitrarily close to one.Direct calculation yields:

It can be observed that the interconnection topology of theei1-subsystems is in accordance with the information exchange topology,represented by digraphGc.Fori∈N,k∈Ni,we assign the positive valueaikto edge(k,i)inGc.DenoteCas the set of all simple loops inGcandCLas the set of all simple loops through the vertices belonging toL.DenoteAOas the product of the positive values assigned to the edges of the loopO∈C.

Note thatbican be designed to be arbitrarily close to 1.According to[27,29],we have the following cyclic-small-gain condition for the interconnectedei1-subsystems:

Lemma 1 presents a small-gain result in digraphs which leads to a condition on the structure of the information exchange digraphGcfor the existence of theaik′s to satisfy(37)and(38).The proof of Lemma 1 can be found in[34].

Lemma 1.For digraphGc,each edge(j,i)is assigned a positive variableaij.DenoteAOas the product of the positive values assigned to the edges of a simple loopO.Fori∈N,denoteC(i)as the set of simple loops ofGcthrough vertexi.IfGchas a spanning treeTwith verticesi∗1,···,i∗qas the roots,then for any∈＞0,there existaij＞0 fori∈N,j∈Ni,such that

Based on Lemma 1,if the information exchange digraphGchas a spanning tree with(some of)the informed agents as the roots,then the closed-loop distributed system satisfies the cyclic-small-gain condition.The main result of the paper is given by Theorem 1.

Theorem 1.Consider the multi-agent system in the form of(1)～(3)satisfying Assumptions 1 and 3.If there is at least one informed agent,i.e.,L/=∅,and the communication digraphGchas a spanning tree with the informed agents as the roots,then we can design distributed control laws defined by(18)～(23)such that all the signals in the closed-loop multiagent system are bounded,and the outputyiof each agentican be steered to within an arbitrarily small neighborhood of the desired agreement valuey0.Moreover,ifwi=0 fori∈N,then each outputyiasymptotically converges toy0.

Proof.IfGchas a spanning tree with vertices belonging toLas the roots,then according to Lemma 1,there exist positive constantsaiksatisfying(35),(37)and(38).Then,with the cyclic-small-gain theorem in[27],the closed-loop distributed system is UO and IOS withwias the inputs andei1′s as the outputs.With Assumption 2,the external disturbanceswiare bounded.The boundedness of the signals of the closed-loop distributed system can be directly verified under Assumption 2.

By designing the IOS gainsχiarbitrarily small(this can be done by using the technique proposed in Section III),the influence of the external disturbanceswican be made arbitrarily small,and under Assumption 2,theei1′s can be driven to within arbitrarily small neighborhoods of the origin.Recallei1=yi−y0.As a result,eachyican be driven to within an arbitrarily small neighborhood ofy0.In the case ofwi=0 fori∈N,it can be proved that the closed-loop multiagent system is globally asymptotically stable at the origin[35]and each outputyiasymptotically converges toy0.□

Remark 3.The proposed design is capable of dealing with both the uncertainties and external disturbances in the system dynamics.No global Lipschitz condition on the system dynamics is assumed.The main result seems to be new even if the agents are with first-order dynamics.Moreover,as shown in the following section,the proposed distributed control strategy is also robust with respect to time-delays and disturbances in information exchange.In this paper,we focus on the ultimate achievement of output agreement,while the converging rate of the closed-loop distributed system is also of interest.Based on IOS cyclic-small-gain methods,it is possible to employ theKLfunctions to represent the converging rates of the subsystems and the closed-loop distributed system.

V.ROBUSTNESS TO TIME-DELAYS AND DISTURBANCES IN INFORMATION EXCHANGE

In this section,we discuss the influence of time-delays and disturbances in information exchange separately.It should be noted that the design is still valid when the discussions are combined for the complex case with the coexistence of time delays and disturbances in information exchange.

A.Communication Delays

If there are communication delays,defined in(16)should be modified as

fort≥0,whereτik:R+→R+represents non-constant time-delays of exchanged information.

In this case,can still be written in the form of=y0−di(t)with fort≥0,which correspond to(33).

We assume that there exists a≥0 such that,fori∈N,k∈Ni,τik(t)≤holds for allt≥0.Due to the time-delay,the critical IOS property(36)for theei1-subsystem should be modified as

Such modification does not affect the validity of the cyclicsmall-gain conditions(37)and(38).By using the time-delay version of the cyclic-small-gain theorem in[29,36],we can still guarantee the IOS of the closed-loop multi-agent system with theei1′s as the outputs and thewi′s as the inputs.The main result presented in Theorem 1 can still be proved to be valid by following a similar analysis as for the proof of Theorem 1.

B.Disturbances in Information Exchange

In the distributed control system,the information exchanged between the distributed controllers is used for feedback control.If the exchanged information is disturbed,then measurement feedback control issues should be well handled.Thanks to the small-gain design,in this subsection,we show that our distributed control design is also robust with respect to the disturbances in information exchange.

For eachi∈N,k∈Ni,we useλikto represent the bounded time-varying disturbance acting on the signalykwhich is transmitted to agenti.Then,thedefined in(16)should be modified as

fort≥0.

In this case,for the small-gain synthesis,we still rewritein the form of

fort≥0,which correspond to(33).

Note that for any constantcik＞0,

Thus,in the presence of disturbances in information exchange,property(34)can be modified as

where constantsδiandaikare defined as for(34),and constantcikshould be positive.Thus,the critical IOS property(36)for theei1-subsystem can be modified as

The cyclic-small-gain conditions(37)and(38)is still valid if we choose the constantscikwhich are small enough.In this case,the closed-loop multi-agent system is IOS with thewi′s andλik′s as the inputs and theei1′s as the outputs.

Remark 4.An advantage of the small-gain design is that although the communication delay and the disturbance in information exchange are assumed to be bounded,no a priori knowledge on the bounds is needed for the control design and the bounds can be arbitrarily large.

VI.AN EXAMPLE

In this section,we employ an example to show the effectiveness of the cyclic-small-gain approach to distributed control.

Consider a multi-agent system composed of three first-order agents:

fori=1,2,3,wherexi∈R is the state,ui∈R is the control input,and∆i:R→R is an unknown,locally Lipschitz function.In this simple case,statexiis also the output of agenti.The objective is to design distributed control laws for the agents to steer the outputs to the agreement valuey0.Suppose that there exists a nonempty set Ω⊆R such thaty0∈Ω and for eachi=1,2,3,

holds for allxi∈R and allai∈Ω.This assumption corresponds to Assumption 1 for systems in the general form.

For control design,we first defineei=xi−y0.Then,

where the term(∆(ei+y0)−∆(y0))satisfies|∆(ei+y0)−∆(y0)|≤ψ∆i(|ei|).To deal with the uncertain term∆(y0),we employ a dynamic compensator

and considervias the new control input of agenti.We now design a control law by usingei+disuch that each controlled agent is IOS withdias the input andeias the output.Then,following the discussions in Section IV,we can realize distributed control.The design procedure below is based on the method proposed in[32]based on the gain assignment technique.See,e.g.,[25,37−38]for the development of the gain assignment technique.

For the system composed of(52)and(53),we first design a nonlinear observer:

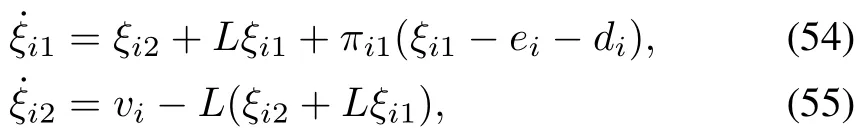
whereρi1:R→R is an odd,strictly decreasing function,Lis a positive constant,variablesξi1andξi2are used to estimateeiandui+∆i(y0)−Lei,respectively.

Defineandas the estimation errors.Then,direct calculation yields:

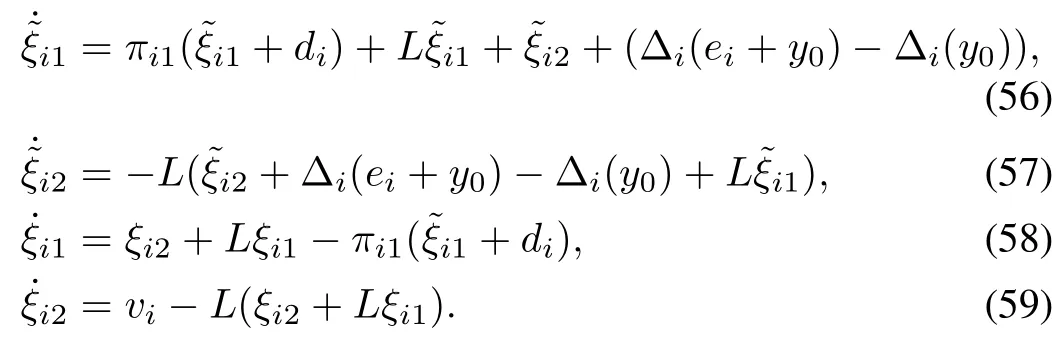
In system(56)～(59),the(ξi1,ξi2)-subsystem is in the well known strict-feedback form[21]involving uncertainties and the-subsystem can be considered as dynamic uncertainty.The stabilization of such system can be solved by using the small-gain design technique proposed in[37].Moreover,we can design a control law such that the closed-loop system is IOS withdias the input andas the output.Speci fic discussions in the context of distributed control can be found in[32].

The control law for system(56)～(59)is designed as

whereπi2,πi3:R→R are odd,strictly decreasing functions.Basically,the termL(ξi2+Lξi1)is used to cancel the same term in(59)and the termπi3(ξi2−πi2(ξi1))is based on the small-gain design.The closed-loop system composed of(56)～(60)has the following IOS property:

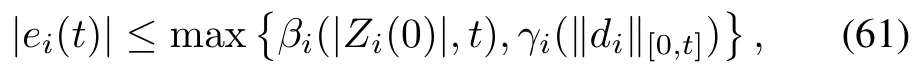
whereandγi∈Kcan be designed to be arbitrarily close to Id.Property(61)corresponds to property(31)for systems in the general form.

In this example,we consider the case with Ω=[−1,1]and the system dynamics satisfying(51)withψ∆i(s)=0.5(s+s2)fors∈R+.Also,the information exchange digraph is assumed as:N1={3},N2={1},andN3={2}.Agent 1 is the only informed agent,i.e.,L={1}.Then,according to(34),disatisfies

whereδ1=1/2,δ2=δ3=1,and the positive constantsa13,a21,a32≥1.By designingγito be in the form ofγi(s)=biswithbi＞1,we have

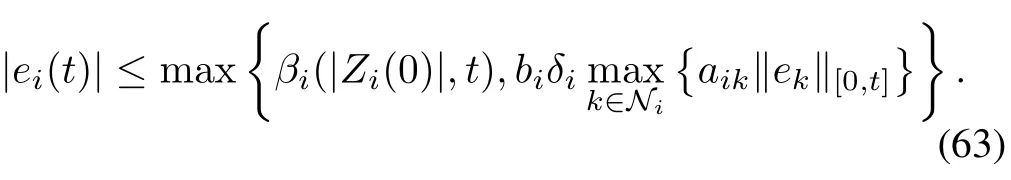
The cyclic-small-gain condition for this system is

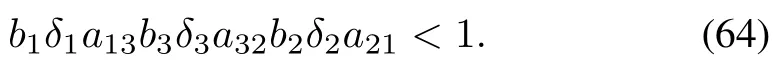
By usingδ1=1/2,δ2=δ3=1 and choosinga13,a21,a32=1,the condition is reduced to

To satisfy condition(65),we chooseL=0.8 and

forr∈R.

We employ a simulation to demonstrate the validity of the theoretical design.In the simulation,the dynamics of the agents are chosen as:,+0.1sin(x2)andThe desired agreement value is chosen asy=1.Figs.1 and 2 show the state trajectories and the control signals of the three agents with initial statesx1(0)=−1,x2(0)=2 andx3(0)=3.

Fig.1.The state trajectories of the agents.

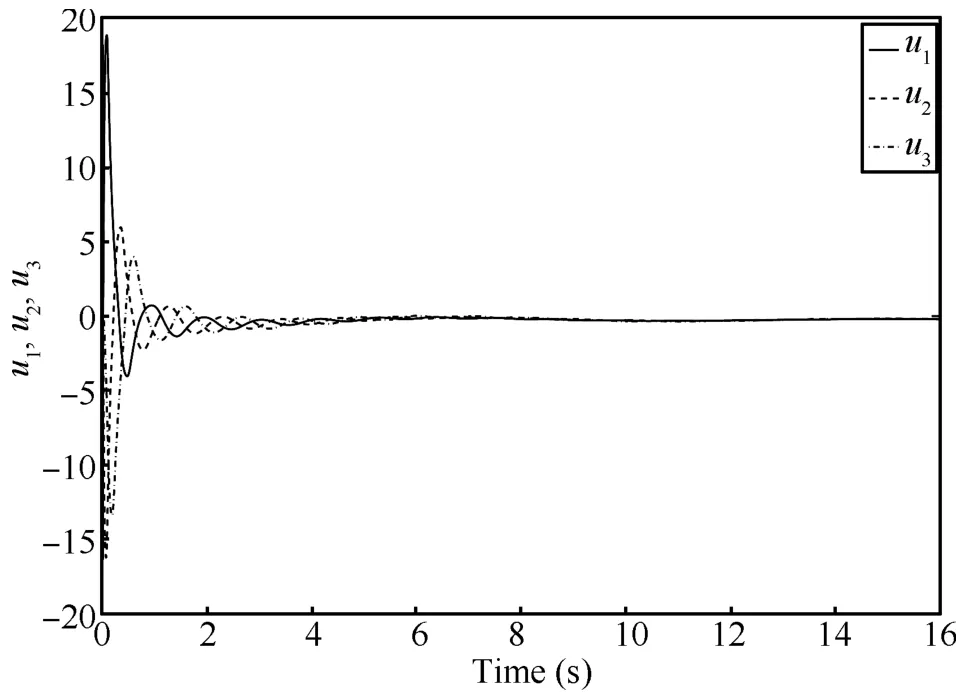
Fig.2.The control signals of the agents.

VII.CONCLUSIONS

This paper has presented a cyclic-small-gain approach to robust distributed control of nonlinear multi-agent systems.With the novel distributed control law,the closed-loop multiagent system is rendered to be IOS with the external disturbances as the inputs.Asymptotic output agreement can be achieved if the system is disturbance-free.The robustness with respect to bounded time-delays and disturbances in information exchange has also been studied.Future research directions may include distributed control with time-varying/switching information exchange topology and the applications to multivehicle systems.Another line of future research is to re fine the current design when the agreement value is time-varying.

REFERENCES

[1]Ogren P,Egerstedt M,Hu X M.A control Lyapunov function approach to multiagent coordination.IEEE Transactions on Robotics and Automation,2002,18(5):847−851

[2]Lin Z Y,Francis B,Maggiore M.State agreement for continuous-time coupled nonlinear systems.SIAM Journal on Control and Optimization,2007,46(1):288−307

[3]Shi G D,Hong Y G.Global target aggregation and state agreement of nonlinear multi-agent systems with switching topologies.Automatica,2009,45(5):1165−1175

[4]Liu S,Xie L H,Zhang H S.Distributed consensus for multi-agent systems with delays and noises in transmission channels.Automatica,2011,47(5):920−934

[5]Arcak M.Passivity as a design tool for group coordination.IEEE Transactions on Automatic Control,2007,52(8):1380−1390

[6]Fax J A,Murray R M.Information flow and cooperative control of vehicle formations.IEEE Transactions on Automatic Control,2004,49(9):1465−1476

[7]Cortes J,Martinez S,Bullo F.Robust rendezvous for mobile autonomous agents via proximity graphs in arbitrary dimensions.IEEE Transactions on Automatic Control,2006,51(8):1289−1298

[8]Siljak D D.Dynamic graphs.Nonlinear Analysis:Hybrid Systems,2008,2(2):544−567

[9]Qu Z H,Wang J,Hull R A.Cooperative control of dynamical systems with application to autonomous vehicles.IEEE Transactions on Automatic Control,2008,53(4):894−911

[10]Su H S,Wang X F,Lin Z L.Flocking of multi-agents with a virtual leader.IEEE Transactions on Automatic Control,2009,54(2):293−307[11]Li T,Fu M Y,Xie L H,Zhang J F.Distributed consensus with limited communication data rate.IEEE Transactions on Automatic Control,2011,56(2):279−292

[12]Wang X L,Hong Y G,Huang J,Jiang Z P.A distributed control approach to a robust output regulation problem for multi-agent systems.IEEE Transactions on Automatic Control,2010,55(12):2891−2895

[13]Wieland P,Sepulchre R,Allgower F.An internal model principle is necessary and sufficient for linear output synchronization.Automatica,2011,47(5):1068−1074

[14]Su Y,Huang J.Cooperative output regulation of linear multi-agent systems.IEEETransactionson Automatic Control,2012,57(4):1062−1066[15]Ogren P,Fiorelli E,Leonard N E.Cooperative control of mobile sensor networks:adaptive gradient climbing in a distributed environment.IEEE Transactions on Automatic Control,2004,49(8):1292−1302

[16]Tanner H G,Jadbabaie A,Pappas G J.Stable flocking of mobile agents,Part I: fixed topology.In:Proceedings of the 42nd IEEE Conference on Decision and Control.Maui,HI:IEEE,2003.2010−2015

[17]Ren W,Beard R W,Atkins E M.Information consensus in multivehicle cooperative control.IEEE Control Systems Magazine,2007,27(2):71−82

[18]Jadbabaie A,Lin J,Morse A.Coordination of groups of mobile autonomous agents using nearest neighbor rules.IEEE Transactions on Automatic Control,2003,48(6):988−1001

[19]Ghabcheloo R,Aguiar A P,Pascoal A,Silvestre C,Kaminer I,Hespanha J.Coordinated path-following in the presence of communication losses and time delays.SIAM Journal on Control and Optimization,2009,48(1):234−265

[20]Xin H H,Qu Z H,Seuss J,Maknouninejad A.A self organizing strategy for power flow control of photovoltaic generators in a distribution network.IEEE Transactionson Power Systems,2011,26(3):1462−1473

[21]Krstic M,Kanellakopoulos I,Kokotovic P V.Nonlinear and Adaptive Control Design.New York:John Wiley and Sons,1995

[22]Siljak D D.Decentralized Control of Complex Systems.Boston:Academic Press,1991

[23]Sontag E D.Smooth stabilization implies coprime factorization.IEEE Transactions on Automatic Control,1989,34(4):435−443

[24]Sontag E D.Input to state stability:basic concepts and results.Nonlinear and Optimal Control Theory.Berlin:Springer-Verlag,2007.163−220

[25]Jiang Z P,Teel A R,Praly L.Small-gain theorem for ISS systems and applications.Mathematics of Control,Signals and Systems,1994,7(2):95−120

[26]Sontag E D,Wang Y.Notions of input to output stability.Systems and Control Letters,1999,38(4−5):235−248

[27]Jiang Z P,Wang Y.A generalization of the nonlinear small-gain theorem for large-scale complex systems.In:Proceedings of the 7th World Congress on Intelligent Control and Automation.Chongqing,China:IEEE,2008.1188−1193

[28]Liu T F,Hill D J,Jiang Z P.Lyapunov formulation of ISS cyclic-smallgain in continuous-time dynamical networks.Automatica,2011,47(9):2088−2093

[29]Karafyllis I,Jiang Z P.Stability and Stabilization of Nonlinear Systems.London:Springer,2011

[30]Jiang Z P,Mareels I M Y,Wang Y.A Lyapunov formulation of the nonlinear small-gain theorem for interconnected ISS systems.Automatica,1996,32(8):1211−1214

[31]Liu T F,Jiang Z P,Hill D J.Decentralized output-feedback control of large-scale nonlinear systems with sensor noise.Automatica,2012,48(10):2560−2568

[32]Liu T,Jiang Z P.Distributed output-feedback control of nonlinear multiagent systems.IEEE Transactions on Automatic Control,2013,58(11):2912−2917

[33]Jiang Z P,Repperger D W,Hill D J.Decentralized nonlinear outputfeedback stabilization with disturbance attenuation.IEEE Transactions on Automatic Control,2001,46(10):1623−1629

[34]Liu T F,Jiang Z P.Distributed formation control of nonholonomic mobile robots without global position measurements.Automatica,2013,49(2):592−600

[35]Khalil H K.Nonlinear Systems(3rd Edition).New Jersey:Prentice-Hall,2002

[36]Tiwari S,Wang Y,Jiang Z P.A nonlinear small-gain theorems for

large-scale time-delay systems.Dynamics of Continuous,Discrete and Impulsive Systems Series A:Mathematical Analysis,2012,19:27−63

[37]Jiang Z P,Mareels I M Y.A small-gain control method for nonlinear cascade systems with dynamic uncertainties.IEEE Transactions on Automatic Control,1997,42(3):292−308

[38]Praly L,Wang Y.Stabilization in spite of matched unmodeled dynamics and an equivalent definition of input-to-state stability.Mathematics of Control,Signals and Systems,1996,9(1):1−33