Distributed Self-triggered Control for Consensus of Multi-agent Systems

Hao ZhangGang FengHuaicheng YanQijun Chen

I.INTRODUCTION

RECENTLY,there has been an increasing interest in event-triggered feedback control systems[1−9].In the event-triggered control,data transmission or control actuation is executed after the occurrence of an event generated by an event-triggering mechanism.The event-triggering mechanism often depends on a well-defined event-triggering condition where the measurement error plays an essential role.When the magnitude of the measurement error reaches the prescribed threshold,an event is triggered.It is noted that the eventtriggered technique can reduce resource usage and provide a higher degree of robustness.However,in many cases it requires dedicated hardware to monitor the plant permanently,which is not available in many general purpose devices.This motives the development of self-triggered control for digital platforms[10−13].In self-triggered control,the next update time of the controller is computed at the previous one,without having to keep track of the measurement error that triggers the execution between two consecutive update instants.Due to its advantages,self-triggered control of multi-agent systems(MASs)has been receiving more and more attention.For example,in[10,12],some novel self-triggered control strategies for MASs were proposed,under which MASs achieved average consensus.It can be observed from those existing works that self-triggered controller for MASs available nowadays are based on static state-feedback under a restrictive assumption that all the agents′states can be measured.It can also be observed that individual agent dynamics are assumed to be a single-integrator.Compared with the conventional eventtriggered control on MASs[14−15],continuous measurement and communication are not required in this paper,thus some actuation power and communication resource might be saved.To the best of our knowledge,there are few works either on self-triggered control for MASs with general linear dynamics based on state feedback or on output feedback.This motivates this study.

In this paper,we study the consensus problem of MASs with general linear dynamics via distributed self-triggered control.Some novel distributed self-triggered controllers are proposed for MASs′asymptotically consensus.Both state feedback and output feedback distributed self-triggered consensus problems are investigated respectively,which help save the resource usage while guarantee a satisfactory consensus performance.The rest of the paper is organized as follows.In Section II,the problem under study is formulated.Sections III and IV provide the main results of this paper,that is,distributed self-triggered control laws based on state feedback and output feedback schemes,respectively.An example is presented in Section V to illustrate the effectiveness of the proposed control methods.Finally,the conclusions are given in Section VI.n

Notations 1.For vectorx=col(x1,···,xn)∈Rand matrixA=[aij]n×n∈Rn×n,‖x‖and‖A‖denote 2-norms ofxandA,respectively.A real matrixP＞0(P＜0)denotes a positive(negative)-definite matrixP.MTdenotes the transpose of matrixM.The identity matrix of ordermis denoted asIm.Moreover,matrices are assumed to have compatible dimensions if not explicitly stated.A⊗Bdenotes the Kronecker product of matricesAandB.1denote the column vector with all entries equal to one.N denotes the set of positive integers.

II.PROBLEM FORMULATION

The communication topology among agents is represented by an undirected graphG=(V,E,A),whereV={υ1,···,υN}is the set of nodes with the node indices belonging to a finite index setI={1,···,N}andE⊆V×Vis the set of unordered pairs of nodes,called edges.Two nodesυi,υjare adjacent,or neighboring,if(υi,υj)is an edge of graphG.A path onGfrom nodeυi1to nodeυilis a sequence of edges of the form(υik,υik+1),k=1,···,l−1.A graph is called connected if there exists a path between every pair of distinct nodes.The adjacency matrixA=[aij]∈RN×Nis the matrix with nonnegative adjacency elementsaijand zero diagonal elements.If edge(υi,υj)∈E,then nodeυjis called a neighbor of nodeυiandaij＞0⇔(υi,υj)∈E.The neighbor index set of agentυiis denoted byNi={j∈I|(υj,υi)∈E}.The degree matrix ofGis given by∆=diag{∆1,∆2,···,∆N},whereMatrixL=∆−Ais the Laplacian matrix of graphG.IfGis connected,its Laplacian matrix has a single zero eigenvalue and the corresponding eigenvector is1and the eigenvalues ofLare denoted by 0=λ1＜λ2≤···≤λN.

In this paper,the consensus problem for a group ofNidentical agents with general linear dynamics is investigated,which can be described by

wherexi(t)∈Rnis the state,ui(t)∈Rpis the control input,yi(t)∈Rqis the measured output,A,BandCare constant matrices with compatible dimensions.Assume that(A,B)is controllable and(A,C)is observable.Protocolui(t)is said to solve the consensus problem asymptotically,if the states of agents satisfy

In this paper,both distributed self-triggered state feedback and output feedback control laws are proposed.

III.DISTRIBUTED SELF-TRIGGERED CONTROL BASED ON STATE FEEDBACK

In self-triggered control,each control task triggers its next release based on the value of the last sampled measurement.If all the states of agents are measurable,the distributed selftriggered state feedback control law is designed as

whereµis a positive scalar andF∈Rp×nis the feedback gain matrix.

Remark 1.It is noted that the controller used in most existing works on event-triggered control of MASs[2,8,10]is triggered at the neighbors′event time,i.e.,ui(t)=whereargThus for eachis the last event time of agentj.However,controller(3)is triggered only at the event time of itself.

The sequence of execution instants for agentiis denoted byThe state measurement error is defined as

whereThe closed-loop system of(1)and(3)is

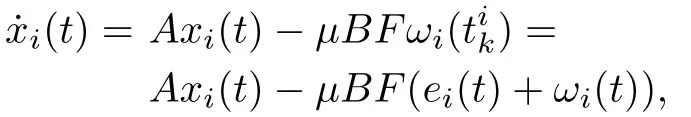
which can be written in a compact form

where=,andBy multiplying both sides of(5)by,one has

thus

Then we have the following result.

Theorem 1.Assume that the communication graphGis connected.Givenδ＞0,consider the controller gainF=BTP,whereP＞0 is a solution of the Riccati equation

and the triggering instant is chosen such that

whereµis sufficiently large such that=,with 0i＜1 and 0＜,thenNagents in(1)will reach consensus under the control law(3).

Proof.Consider a Lyapunov function candidate for the closed-loop system as

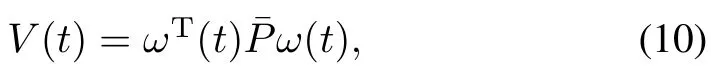
whereandP＞0.Calculating the time derivative ofV(t)along the solution of(5),one has

SinceGis connected,zero is a simple eigenvalue ofLand all the other eigenvalues are positive.LetU∈RN×Nbe a unitary matrix such thatUTLU=Λ=diag{0,λ2,···,λN}.The right and left eigenvectors ofLcorresponding to the zero eigenvalue are1and1T,respectively.One can chooseU=and,withX1∈RN×(N−1)andX2∈R(N−1)×N.Let.Notice thatω1(t)+···+ωN(t)=0.Thenξ1(t)=0,and thus

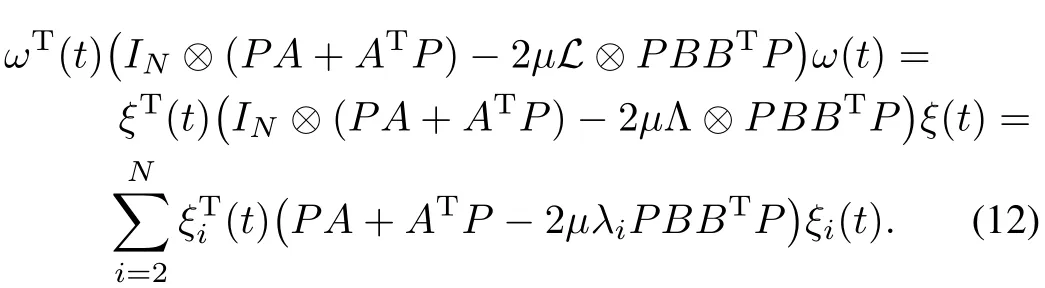
By choosing sufficiently largeµsuch that,one has

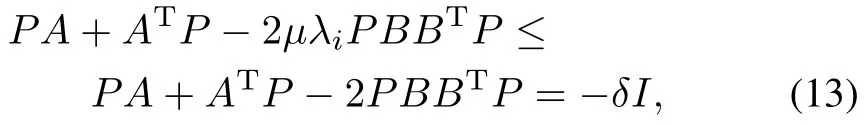
where the last equation is derived by using(8).It follows from(12)that

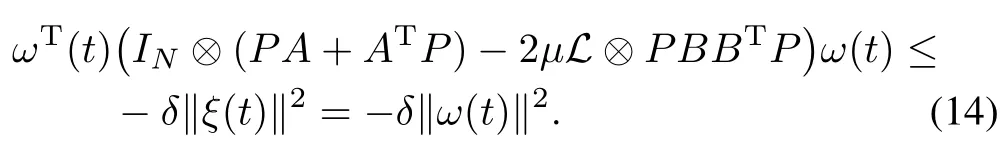
From(12)to(14)and noticingaij=aji,one has

whereθis a positive scalar defined in Theorem 1.For eachi,define the triggering condition as

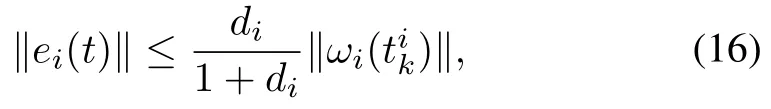
wherediis defined in Theorem 1.It follows from(4)and(16)that.Thus

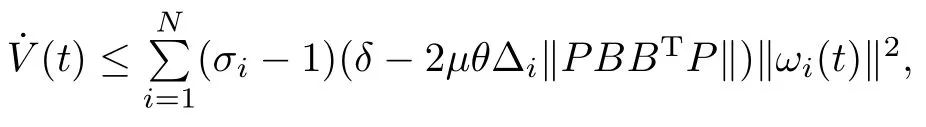
thenfor any 0＜σi＜1 and 0＜θ＜.It follows from(4)and(7)that

So the evolution offoris bounded by the solution of

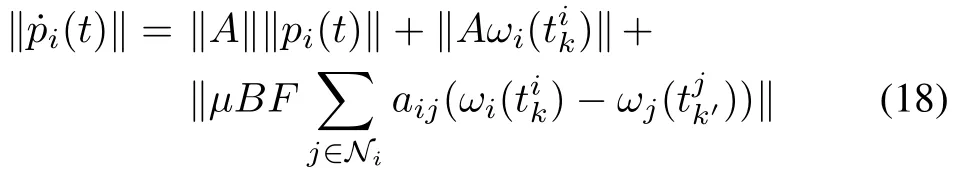
with.Thus the corresponding solution of(18)is given by

From(16)and(19),one has thatan upper bound of the time forto evolve from 0 tosatis fies

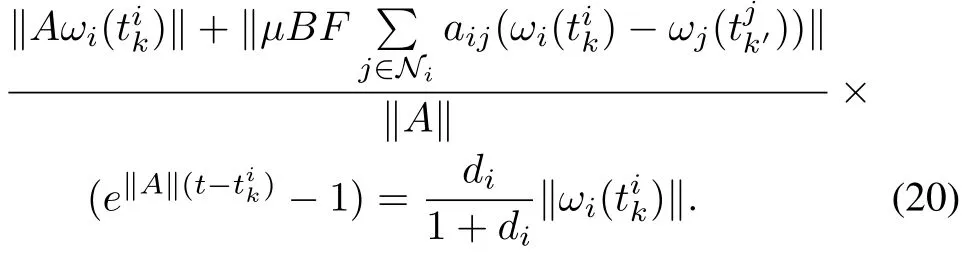
Thus the triggering time can be chosen as

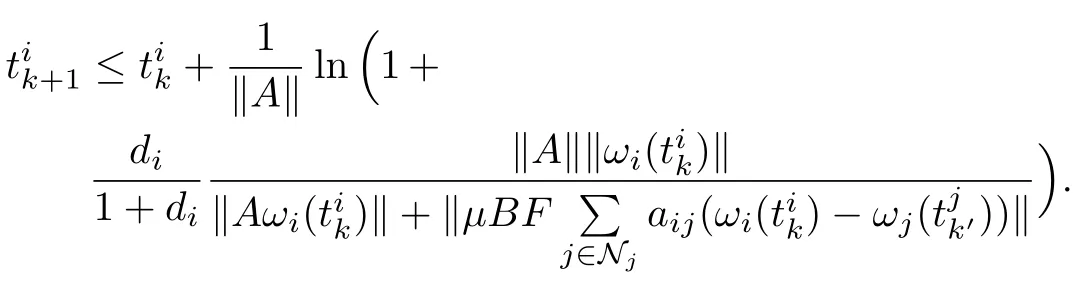
IV .DISTRIBUTED SELF-TRIGGERED OUTPUT FEEDBACK CONTROL

If some states of the system cannot be measured,control strategies based on state feedback cannot be used.In this case,control schemes based on output feedback should be used.A state observer can be designed as

whereis the observer state,is the observer measured output,L∈Rn×qis a constant matrix to be designed.Define

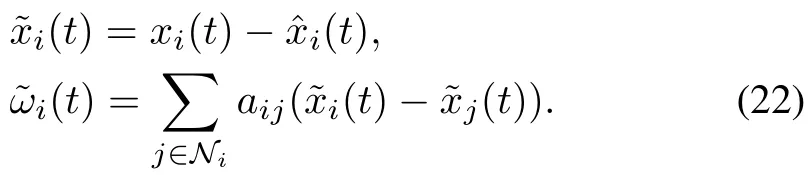
The distributed self-triggered observer-based output control law is designed as

whereP.The state measurement error is defined as

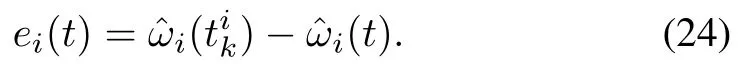
By multiplying both sides of the closed-loop system of(1)and(23)byL⊗Im,one has

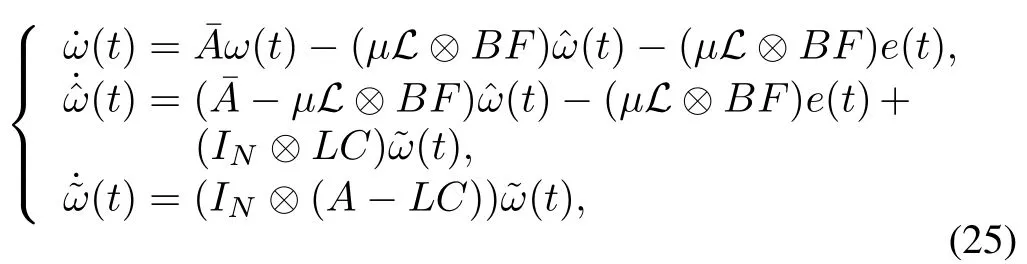
whereandIt can be observed from the third equation in(25)thatwill approach zero asymptotically ifLis designed to makeA−LCHurwitz.Thus the stability of the second equation in(25)is equivalent to the stability of the following system

Then we get the following result.

Theorem 2.Assume that the communication graphGis connected.LetLbe any gain matrix such thatA−LCis Hurwitz.If the triggering time is chosen such that

whereτsatisfies the equation

withµis sufficiently large such thatµλ2≥1,F=BTP,withP＞0 being a solution of the Riccati equation(8),anddiis defined in Theorem 1,thenNagents in(1)will reach consensus under the control law(23).

Proof.Consider a Lyapunov function candidate for the closed-loop system as

whereis defined in(10).Calculating the time derivative ofV(t)along the solution of(26),one has

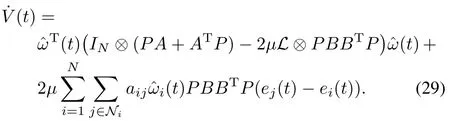
Similar to the analysis from(12)to(15),one has

Thus for agentithe triggering condition can be designed as

wherediis defined in Theorem 1.It follows from(24)and(30)that

Thus

thenfor any 0＜σi＜1 and 0＜θ＜

It follows from(24)and(30)that

which implies

One further has

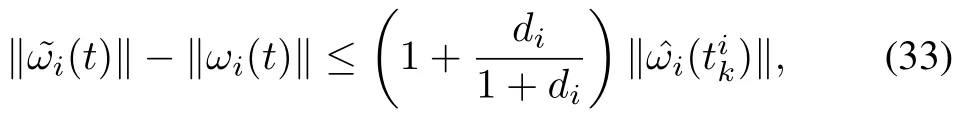
thus

From(24)and the first equation in(25),one has

then

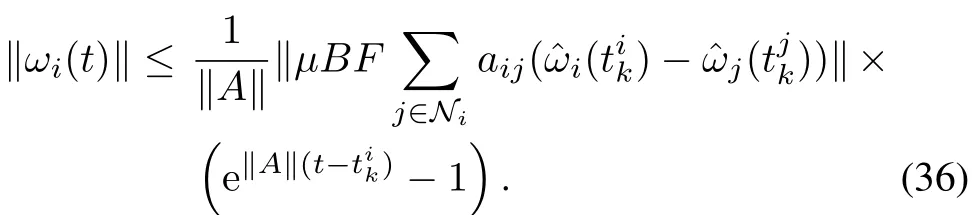
From(24)and the second equation in(25),one has

Substituting(34)and(36)into(37),one has

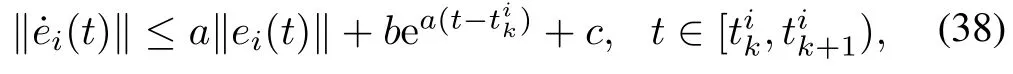
wherea,bandcare defined in Theorem 2.

So the evolution of‖ei(t)‖fort∈[tik,tik+1)is bounded by the solution of

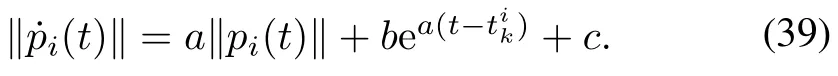
With,the corresponding solution of(39)is given by

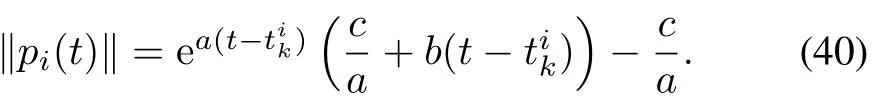
From(31)and(40),one has thatthe upper bound of the time for‖to evolve from 0 tosatis fies

which can be rewritten as

where.Sinceapproaches zero andbτapproaches positive in finity asτgoes to in finity.Then there exists a positive scalarτthat solves the equation.Thus the triggering time can be chosen as.The proof is thus completed.□

V.ASIMULATION EXAMPLE

In this section,an example is provided to validate the effectiveness of the proposed control approaches.Consider a network described as follows

The Laplacian matrix of the network is given by

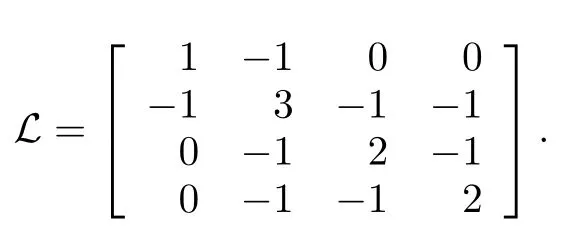
Chooseσ1=0.1,σ2=0.2,σ3=0.3,σ4=0.4,δ=0.01,θ=0.002.By solving Riccati(8),one hasF=[0.2663 0.2214 0.0499 1.2022].Using controller(23)and triggering condition(27),the states and states measurement errors of multi-agent systems are shown in Figs.1 and 2,respectively.Chooseσ1=0.1,σ2=0.2,σ3=0.3,σ4=0.4,α=0.01,θ=0.002,for output feedback control.Using controller(23)and triggering condition(27),the states and states measurement errors of multi-agent systems are shown in Figs.3 and 4,respectively.

Fig.1.States of MASs using distributed self-triggered control.

It can be observed from Figs.2 and 4 that the consensus errors approach zero as time goes to in finity.That is,the consensus is achieved.

Fig.2.States measurement errors of MASs using distributed selftriggered control.

Fig.3.States of MASs using distributed self-triggered output feedback control.

Fig.4.States measurement errors of MASs using distributed selftriggered output feedback control.

VI.CONCLUSION

This paper provides some solutions for the consensus problem of identical agents with an event-based control and communication.In order to reduce the control update times and the communication effort,distributed self-triggered cooperative control strategies based on state feedback and output feedback are proposed,respectively,and it is shown that consensus can be reached in both cases for all connected communication graphs.Future work includes extending the proposed approach to MASs with heterogeneous dynamics and agent with uncertainty.

REFERENCES

[1]Heemels W P M H,Johansson K H,Tabuada P.An introduction to eventtriggered and self-triggered control.In:Proceedings of the 51st IEEE Conference on Decision and Control.Maui,HI:IEEE,2012.3270−3285

[2]Dimarogonas D V,Johansson K H.Event-triggered control for multiagent systems.In:Proceedings of the 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference.Shanghai,China:IEEE,2009.7131−7136

[3]Donkers M C F.Output-based event-triggered control with guaranteedL∞gain and improved event-triggering.In:Proceedings of the 49th IEEE Conference on Decision and Control.Atlanta,Georgia:IEEE,2010.3246−3251

[4]Donkers M C F,Heemels W P H H.Output-based event-triggered control with guaranteedL∞gain and improved and decentralized event-triggering.IEEE Transactions on Automatic Control,2012,57(6):1362−1376

[5]Tabuada P.Event-triggered real-time scheduling of stabilizing control tasks.IEEE Transactions on Automatic Control,2007,52(9):1680−1685

[6]Mazo M,Tabuada P.Decentralized event-triggered control over wireless sensor/actuator networks.IEEE Transactions on Automatic Control,2011,56(10):2456−2461

[7]Fan Y,Feng G,Wang Y,Song C.Distributed event-triggered control of multi-agent systems with combinational measurements.Automatcia,2013,49(2):671−675

[8]Min Hai-Bo,Liu Yuan,Wang Shi-Cheng,Sun Fu-Chun.An overview on coordination control problem of multi-agent system.ActaAutomatica Sinica,2012,38(10):1557−1570(in Chinese)

[9]Yan Wei-Sheng,Li Jun-Bing,Wang Yin-Tao.Consensus for damaged multi-agent system.Acta Automatica Sinica,2012,38(11):1880−1884(in Chinese)

[10]Dimarogonas D V,Frazzoli E,Johansson K H.Distributed eventtriggered control for multi-agent systems.IEEE Transactions on Automatic Control,2012,57(5):1291−1297

[11]Zhang J H,Zhao D Y,Wang D K.Observer-based control for linear system with event-triggered sensor.In:Proceedings of the 31st Chinese Control Conference.Hefei,China:IEEE,2012.5747−5752

[12]Dimarogonas D V,Frazzoli E,Johansson K H.Distributed self-triggered control for multi-agent systems.In:Proceedings of the 49th IEEE Conference on Decision and Control.Atlanta,GA:IEEE,2010.6716−6721

[13]Anta A,Tabuada P.To sample or not to sample:self-triggered control for nonlinear systems.IEEE Transactions on Automatic Control,2010,55(9):2030−2042

[14]Liu Z X,Chen Z Q.Reaching consensus in networks of agents via eventtriggered control.Journal of Information and Computational Science,2011,8(3):393−402

[15]Liu Z X,Chen Z Q.Event-triggered average-consensus for multiagent systems.In:Proceedings of the 29th Chinese Control Conference.Beijing,China:IEEE,2010.4506−4511