An Overview of Distributed High-order Multi-agent Coordination

Jie HuangHao FangLihua DouJie Chen

I.INTRODUCTION

THE study of multi-agent coordination was perhaps first motivated by the group phenomena in nature[1],the work in statistical physics[2]and distributed computing[3].Since that,in particular for the past two decades,cooperative control of multi-agent systems has received increasing attention by the fact that many bene fits can be obtained when a single complicated agent is equivalently replaced by multiple simpler agents.And in the recent ten years,numerous results have been obtained to solve a variety of multi-agent cooperative control problems.In early works(before and around the year 2000),most of them assumed the availability of global team information,the ability to plan group actions in a centralized manner,and/or perfect and unlimited communication among the agents;see[4−9].However,the centralized coordination schemes do not work well for the reason that the real-world communication topologies are usually not fully connected,especially when the group of agents have large scale members.Due to the disadvantage of the centralized coordination schemes,the distributed manner was investigated.In the distributed control of a group of autonomous agents,the main objective is typically to have the whole group of agents working in a cooperative fashion through a distributed protocol.These controllers are distributed in the sense that the controller design for each agent only requires relative state information between itself and its neighbors.Hence,cooperative or coordination refers to a close relationship among all agents in the group where information sharing plays a crucial role.The distributed approach has many advantages for achieving cooperative group performance,especially with low operational costs,less system requirements,high robustness,strong adaptivity,and flexible scalability.The control theory of multi-agent systems can be applied to many practical engineering applications such as cooperative control of unmanned ground/air/underwater vehicles[10−12],distributed sensor networks[13−14],aggregation and rendezvous control[15],attitude alignment of spacecraft[16−17]and so on.Therefore,cooperative control of multi-agent systems has been widely recognized and appreciated,and numerous results have been obtained to solve multi-agent cooperative control problems.There are several reviews on multi-agent systems given in[18−25]and the classic books in[26−33].

Among the existing works mentioned above,most of them studied only the first-and second-order dynamics.Recently,some researchers turned to focus on the high-order multi-agent systems coordination.One motivation for studying higherorder consensus comes from observing the behavior of flocks of birds[34].It is often noted that such flocks fly in formation,maintaining a nominal separation from each other,but each traveling with the same velocity vector.It can be shown that second-order coordination can reproduce the behavior of a separation and common velocity under information exchange.However,sometimes a bird flock abruptly changes direction,perhaps when one of them suddenly perceives a source of danger or food.Clearly,the birds in this setting need to build consensus on not only their relative position and velocity,but also on their acceleration.In addition,in engineering,many systems are modeled by higher-order dynamics.For example,the jerk systems,described by third-order differential equations,are of particular interest in mechanical engineering[35].A single link flexible joint manipulator is well modeled by a fourth-order nonlinear system[36].To sum up,in many practical applications,it is not acceptable to model the plant dynamics with only single-or double-integrator dynamics.So it is necessary to extent the coordination problem from lowerorder dynamics to high-order ones.

This paper reviews the major results and recent progress in distributed high-order linear and nonlinear multi-agent coordination.Specifically,this paper reviews the research results in the following directions,which are not independent but actually may have overlapping to some extent.In Section II,the necessary preliminaries concerning the cooperative control problem are given,especially the graph theory.In Section III,the coordination of high-order linear multi-agent systems are considered.First,the typical and basic model of the high-order linear multi-agent systems is investigated.Second,coordination of high-order linear systems with disturbance are discussed.The remaining subsections describe the coordination of discrete-time and general high-order linear time-invariant(LTI)systems.In Section IV,the coordination of high-order nonlinear multi-agent systems is investigated,including the typical high-order nonlinear system,high-order nonholonomic systems and nonlinear systems in the Brunovsky form.The last section gives a short discussion to summarize the paper and propose several promising research directions along with some open problems that are deemed important for further investigations.

II.PRELIMINARIES

Graph theory is a very useful mathematical tool in the research of coordination of multi-agent systems.When a team ofNagents labeled as systems 1 toNare considered,the topology of a communication network can be expressed by a graph,either directed or undirected,according to whether the information flow is unidirectional or bidirectional.

A weighted graph(undirected graph or digraph)G=(V,E,A)consists of a nonempty finite set ofNnodesV={v1,v2,···,vN},a set of edgesE⊆V×V,and a weighted adjacency matrixA=[aij]∈RN×N,whereVis a set of the indices of the systems andEis a set of edges that describe the communication between the agents.In a directed graph,if(vi,vj)∈E,theniis neighboring toj,meaning systemjcan obtain information from systemi.And it can be said thatviis the parent node andvjis the child node.The set of neighbors of nodeiis denoted asNi={j|(vj,vi)∈E}.In most existing literature,self edges(vi,vi)are assumed to be not allowed.Each entryaijof the adjacency matrixAis the weight associated with edge(vj,vi)andaij＞0 if(vj,vi)∈E.Otherwise,aij=0.For an undirected graphG,the weighted adjacency matrixA=[aij]N×Nsatisfiesaij=aji＞0.Its Laplacian matrixL=[Lij]is defined as

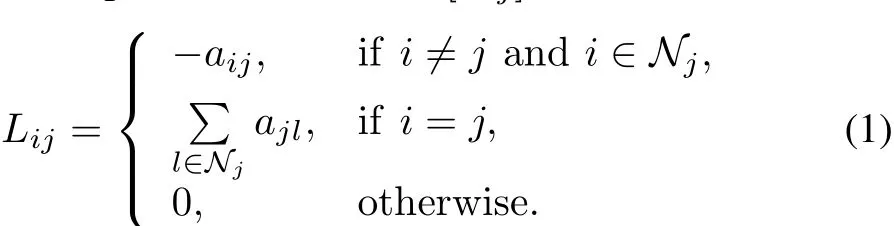
Define the in-degree of nodeiasand the in-degree matrix asD=diag{di}∈RN×N.Then,the graph Laplacian matrix isL=D−A.Let 1N=[1,1,···,1]T∈RN;then,L1N=0.Accordingly,define the out-degree of nodeiasPand the out-degree matrix asDo=diag.Then,the graph column Laplacian matrix can be defined asLo=Do−AT.A node is balanced if its indegree equals its out-degree.A directed graph is balanced if all its nodes are balanced.Since for undirected graph,AT=A,all undirected graphs are balanced.

In a directed graph,a sequence of successive edges in the form{(vi,vk),(vk,vl),···,(vm,vj)}is a direct path from nodeito nodej.An undirected path is defined similarly.A digraph is said to have a spanning tree,if there is a root nodeir,such that there is a directed path from the root to any other node in the graph.A digraph is said to be strongly connected,if there is a direct path from nodeito nodej,for all distinct nodesvi,vj∈V.A digraph has a spanning tree if it is strongly connected,but not vice versa.A digraph(or undirected graph)is said to be connected,if for any orderless pair of nodes,there is a directed(or undirected)path connecting them.For a digraph,its underlying graph is the graph obtained by replacing all directed edges with undirected edges.A digraph is weakly connected if its underlying graph is connected.More details can be found in the bookGraph Theoretic Methods in Multiagent Networks[33].

III.COORDINATION OF HIGH-ORDER LINEAR SYSTEMS

A.Coordination of High-order Integrator Linear Systems

Basic high-order linear multi-agent systems can be represented by integrator chained systems in strict-feedback form as

where,k=0,1,···,l−1,l≥3 denotes the states of the systems,ui∈Rmis the control input of thej-th system,anddenotes thek-th derivative ofξiwithThis model generalizes the single-integrator and double-integrator dynamics.

The basic idea of a consensus algorithm is to impose similar dynamics on the information states of each high-order system.If the communication network among systems allows continuous communication or if the communication bandwidth is sufficiently large,then the information state update of each system is modeled using a differential equation.On the other hand,if the communication data arrive in discrete packets,then the information state update is modeled using a difference equation.The fundamental consensus algorithms for highorder linear systems can be shown as follows

wherekij＞0,γk＞0,gii=0,andgijis 1 if information f l ows from systemjto systemiand 0 otherwise.Consensus is reached among themsystems if,k=0,1,···,l−1,∀i/=j.Letξ=[ξ1,···,ξn]T.By applying consensus algorithm(3),(2)can be written in matrix form as

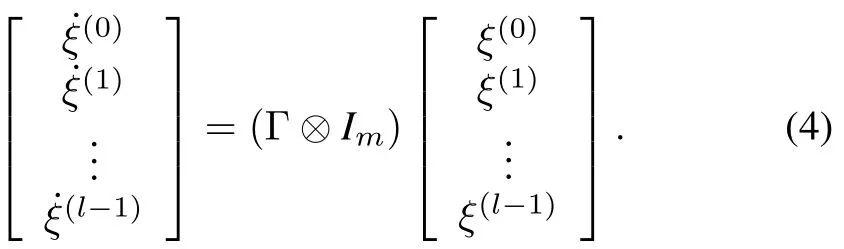
Due to the characteristics of multi-agent systems,the closedloop system can be expressed by the vector form,therefore matrix theory has been frequently used in the stability analysis of linear systems′distributed coordination.As a fundamental cooperative control problem,the leaderless consensus was considered first in literature.In[34,37],Ren et al.proposed a class ofl-order(l≥3)consensus algorithms and showed necessary and sufficient conditions under which each information variable and their high-order derivatives converged to common values.They also introduced the idea of high-order consensus with a leader and the concept of anl-order modelreference consensus problem,where each information variable and their high-order derivatives not only reach consensus but also converge to the solution of a prescribed dynamic model.However,it cannot solve the rendezvous problem because of the non-zero velocity when consensus is achieved.Jiang et al.investigated the consensus problem for multiagent systems with individual agents modeled by high-order integrators under fixed/switching topology and zero/nonzero communication time-delays[38].Consensus of high-order integrators multi-agent systems with time-delays and switching topologies were studied by Yang et al.It was shown that consensus can be reached with arbitrarily bounded time-delays even though the communication topology might not have spanning trees[39].Zhang et al.also investigated consensus of high-order multi-agent systems.Different from the existing protocols in[34,37],a dynamic neighbour-based protocol was proposed,which only uses the relative information of the first states of agents by extending second-order protocols from the literature.Sufficient conditions were derived under which all agents reach consensus asymptotically[40].He et al.proposed a linear consensus protocol for solving such a consensus problem,which includes two parts:a feedback controller and interactions from the neighbours.A sufficient and necessary condition for consensus in high-order systems was obtained.They proposed the control protocolui=ui1+ui2,wherePis the feedback controller,bis a non-zero constant to be determined.AndAs special cases,the criteria for second-and third-order systems were given,in which the exact relationship between feedback gain and system parameters was established.The introduced parameters in the consensus protocol makes the design of the feedback gain more flexible[41].Leader-following consensus problems of high-order multi-agent linear systems with noises and time delays have been discussed in[42].Under the condition that the topologies are undirected,some consensus conditions were obtained.

The literature mentioned above are under the matrix theory approaches based framework,for the model of the multi-agent systems are high-order linear systems in a chained form.Moreover,there are still some other methods to deal with the highorder linear system cooperative control problems,such as the famous backstepping technique.In the backstepping technique combining graphic theory,owing to the structure character of the lower-triangular strict-feedback formed system,the highrank state of each differential equation is used as virtual control.Then,the consensus control problem for the higherorder multiple systems can be broken into a sequence of design problems for multiple lower order subsystems.In addition,the backstepping technique combining adaptive control method,sliding mode control,neural network method,etc.can solve not only linear systems control problems but also nonlinear control problems[36,43].

B.Coordination of High-order Linear Systems with Disturbance

In some practical applications,multi-agent systems are often subject to various disturbances such as actuator bias,measurement/calculation errors,and variation of communication topology.

A class of high-order linear system with external disturbances can be described as follows[44−48]

wherei(1≤i≤n)denotes the index number of the system,denotes the states of thei-th system.ui∈R is the control input of thei-th system,andwiis the external disturbance.

As for the multi-agent systems with external disturbance,Mo et al.provided the convergence analysis of the consensus problem for multi-agent systems with time delays and external disturbance[44].They proposed a dynamic neighbour-based protocol as follows

for anyi∈{1,2,···,n},whereaij＞0 denotes the edge weight,gk＞0 fork=0,1,···,l−1,andτ＞0 denotes the communication delay.The output functions were defined to combine the relative information by computing from an average of the relative displacements of all agents as follows

And theH∞performance index was defined as follows

whereγis a given positive constant.The approach used in[44]does not need any model transformation,which is different from the results of first-order[45]and second-order multi-agent systems[46].

Liu et al.[47]studied the output consensus problem of thelth-order multi-agent systems with external disturbances in networks with fixed and switching directed topologies,respectively.A controlled output was defined to measure the disagreement of each agent′s measured output to the average one of all agents.The controlled output functions were similar to(7)in[44].The consensus problem can be transformed into anH∞control problem.Then,a distributed protocol was proposed for each agent using its own information and its neighbors′measured outputs,and a closed-loop system was derived with a singular state matrix,which resulted in invalidation of the traditionalH∞theory.Then,they conducted a model transformation by two steps,and obtained an equivalent nonsingular reduced-order system regarding theH∞performance,based on which consensus of the multiagent system was investigated.Specifically,for directed networks with fixed topology,a necessary and sufficient condition was obtained to ensure the output consensus with a givenH∞performance index.This consensus controller is different from the literature mentioned above either;for agenti,only its neighbors′measured outputsare directly obtainable,and the other variables of neighbors would have to be estimated.Thus,it can use the available information(j∈Ni),instead of all-order derivatives of,to design

fori=1,2,···,n,whereKk∈R(k=1,2,···,l)are consensus gains.The role of local negative feed backPis to decrease the modulus of high-order variablesk=2,3,···,l.

However,how to deal with stochastic disturbances in highorder multi-agent systems,or even with stochastic communication topologies,is still a challenging problem.

C.Coordination of Discrete-time High-order Linear Systems

Many practical systems are with discrete-time models,and the high-order discrete-time multiple ones can be described as follows

Suppose that the multi-agent systems(10)considered consists ofNdiscrete-time agents.Each agent at instantkTis regarded as a node in a directed graphG(kT)=(V,E(kT),A(kT)),whereT＞0 is the sampling time,V={v1,···,vN}is the set of nodes,E(kT)⊆V×Vis the set of edges,andA(kT)=[aij(kT)]is a weighted adjacency matrix.Each edge(vj,vi)∈E(kT)denotes an information link from agentvito agentvjat instantkT.The set of the neighbours of theith agent and the Laplacian of the graphG(kT)at timekTare represented byNi(kT)andL(kT),respectively.

Different from[14],the rule for the discrete-time multiagent high-order systems is given as

for anyi∈{1,2,···,n},wherepj＞0 forj=1,2,···,l−1,aij＞0 denotes the edge weight chosen from a finite setandτij(t)∈Z+,τij(t)≤τmax(i/=j)is the communication time-delay fromvjtovifor a given positive constantτmax.Sufficient conditions were derived for the introduced rule to make all agents reach consensus under dynamically changing topologies in[49].It is shown that consensus can be reached,even when the communication topologies are dynamically changing and the corresponding communication graphs have no spanning trees.It is also shown that the communication time-delays do not affect the stability of the multi-agent systems.In[50],leader-following consensus of discrete-time multi-agent systems was considered.And an observer-based protocols was proposed.

D.Coordination of General High-order LTI Systems

Recently,a class of general high-order linear time-invariant(LTI)systems has been considered[51−65].In this kind of multi-agent systems,all the agents have identical multi-input multi-output(MIMO)linear dynamics which can be of any order.The dynamics of theith agent is described by

wherexi∈Rnis the state,ui∈Rpthe control input,andyi∈Rqthe measured output.A,B,Care constant matrices with compatible dimensions,whereCis assumed to have full row rank.

In Sections III-A～III-C,the protocols are based upon all the states of neighboring agents.However,in terms of the general high-order LTI systems,the agent should have inputs as many as the order of the system[51].The output feedback consensus problem has been considered by Scardovi and Sepulchre[52],where all the states of the observer for each agent need to be transmitted to the neighbors,so that the quantity of the transmitted information is the same as the state feedback case.The work by Tuna[53]discussed various conditions for achieving consensus by output feedback,but was limited to static output feedback cases.On the basis of the above work,Seo et al.[54]studied the consensus problem in a generalized environment in the sense that each agent is a multiinput multi-output linear dynamic system which is stabilizable and detectable,and that a dynamic consensus algorithm is proposed that uses only the output information(rather than the full state)from the neighboring agents.The output feedback consensus problem forNidentical linear dynamics was solved in a uni fied manner.By the way,the authors first showed that consensus problem is solved if there exists a stable dynamic f i lter which simultaneously stabilizesN−1 linear dynamic systems in a special form.Next,they proved that there exists such a filter under a very general condition and showed how to construct the filter.In[53],it was assumed that agenticollected the output information of its neighboring agents by the following rule

in whichNi={j∈N:αij/=0}.They also assumed that the collected informationzi(t)is filtered by a stable filterκ(s),and is fed back to agentiby

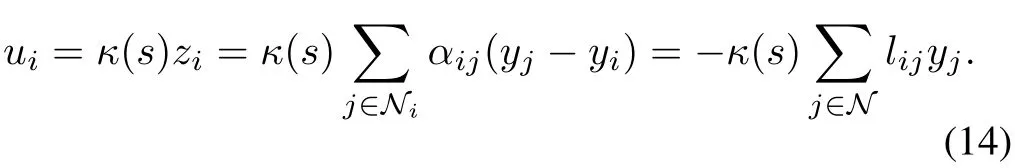
Li[55]considered the consensus problems for both continuous-and discrete-time linear multi-agent systems with directed communication topologies.Distributed reduced-order observer-based consensus protocols were proposed,based on the relative outputs of neighboring agents.A multi-step algorithm was presented to construct a reduced-order protocol,under which a continuous-time multi-agent system whose communication topology contains a directed spanning tree can reach consensus.The algorithm in[55]was further modified to achieve consensus with a prescribed convergence rate.These two algorithms have a favorable decoupling property.In light of the modified algebraic Riccati equation,an algorithm was then given to construct a reduced-order protocol for the discrete-time case.In[56],Wieland et al.considered the problem of reaching static or dynamic consensus over fixed interconnection topologies for multi-agent systems with agents modelled as general LTI systems.The consensus condition of the whole multi-agent systems was derived as stability of some matrices which consist of the agent dynamics and the spectrum of the Laplacian of the corresponding graph.In addition,a meaningful interpretation of the role of the adjoint null space of the Laplacian matrix was given.As far as design was concerned,systematic methods were proposed to choose the gains in the consensus algorithm such that the multi-agent systems reached consensus asymptotically with prespecified convergence rate.In terms of consensus seeking problem of high-order LTI multi-agent systems with fixed and switching topologies,Jiang et al.[57]gave some results.A necessary and sufficient condition was derived for the consensus of the multi-agent systems with fixed topology and zero time-delay.The protocol designs were also discussed respectively for directed and undirected topologies.Under switching topology and zero time-delay,a sufficient condition for the consensus of the multi-agent system was established.In[58],Zeng et al.discussed the consensus problem of a group of general linear agents under an undirected topology.Both input and communication delays were taken into account.The factorization of the characteristic equation of the system into decreased-order factors relied only on the set of eigenvalues of a matrix that describes the structure of the network topology,and simplified the stability analysis considerably.Tang et al.[59]investigated hierarchical distributed control for multiagent systems using approximate simulation.They proposed the distributed control with two parts:one is the local control for coordination,while the other is from the virtual leader.In[60],consensus of high-order linear multi-agent systems using output error feedback was considered.Wang et al.investigated an observer based approach to design a dynamic output error feedback consensus control law.

Recently,one new direction is the formation swarm control for multiple LTI systems.Xi et al.[61−64]considered consensus analysis and design problems for high-order linear time-invariant swarm systems.In[61],consensus problems for high-order continuous-time linear time-invariant swarm systems with directed interaction topologies were investigated.A method to deal with consensus problems was proposed based on state space decomposition.Two subspaces of a complex space were introduced,namely a consensus subspace and a complement consensus subspace.Based on this decomposition,necessary and sufficient conditions for consensus and consensualizability were presented,respectively.An approach for determining and designing the consensus function which may be time-varying was shown.The applications of theoretical results to multi-agent supporting systems were also studied.In[62],the swarm stability problem of high-order linear timeinvariant swarm systems with directed graph topology was dealt with.Consensus problems can be regarded as a specific type of swarm stability problem.Necessary and sufficient conditions for both swarm stability and consensus were also presented.In[63],consensus analysis and design problems for high-order linear time-invariant swarm systems with timevarying delays were dealt with.First,a consensus subspace and a complement consensus subspace were introduced.By state projection onto the two subspaces,consensus problems were converted into simultaneous stabilization problems of multiple time-delayed subsystems with low dimensions,and a method to analyze and design the consensus function was given.Then,sufficient conditions for consensus and consensualization were presented,which included only four linear matrix inequality constraints.At present,it remains a challenging problem to deal with high-order swarm coordinative control problems.

IV .COORDINATION OF HIGH-ORDER NONLINEAR SYSTEMS

As for the high-order multi-agent systems,most of the existing reseaches are only concerned with the integrators chained systems with linear strict-feedback form.Whereas,almost all physical systems are inherently nonlinear,for example,wheeled mobile robots,dynamics of manipulators,etc.,thus the research of cooperative control for high-order nonlinear systems is more practical.What is more,in many practical applications,the dynamics of the systems are usually not only nonlinear but also with uncertainties,thus solving consensus problems for multiple high-order uncertain nonlinear systems would make great sense for practical applications.The matrix theory approaches mentioned above are not applicable to many scenarios,especially for nonlinear systems.Thus the cooperative control of high-order nonlinear systems with uncertainties is more challenging than that of the certain high-order linear ones.Today,there are still few results on cooperative control problems of high-order nonlinear systems.

A.Coordination of Typical High-order Nonlinear Systems

The typical high-order nonlinear multi-agent systems can be described by

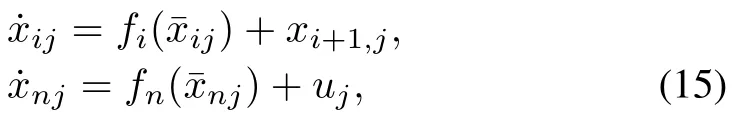
fori=1,···,n−1,whereThe functionfiis smooth and is assumed to be known.uj∈R is the control input of systemj.In[66−67],consensus and tracking problems of multiple high-order nonlinear systems with the model of(15)were considered.Distributed control laws were proposed with the aid of robust control theory,approximationbased control theory and backstepping technique as follows

for 1≤j≤m,whereaji=aij≥δ＞0,z∗j=x∗j−α∗jare error variables of thejth system which are defined by backstepping technique,wherex∗j=[x1j,x2j,···,xnj]T,andα∗j=[α1j,α2j,···,αnj]Tare the virtual controllers of thej-th system in each order,respectively.The protocol(16)makes the states of a group of systems converge to a stationary point.For tracking problem,a robust/adaptive control law(17)were proposed such that the states of the systems could converge to the state of the reference systems

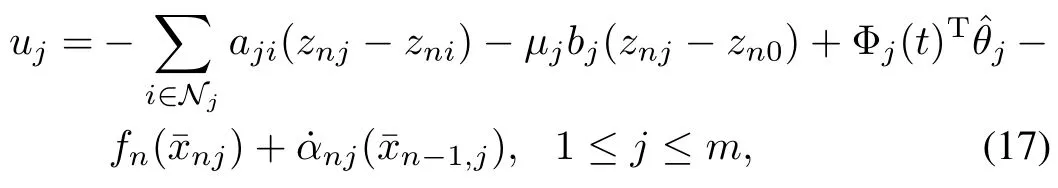
where constantbj≥δ＞0,µj=1 if the states of the reference systems is available to systemj,µj=0 otherwise.is the key item for consensus seeking by adaptive control theory.

Although the backstepping has become one of the most popular design methods for the strict-feedback systems,it has the“explosion of complexity”problem,which is caused by the repeated differentiations of virtual controllers in each backstepping design step.To overcome this problem,a dynamic surface design technique combing neural network technique was proposed for strict feedback systems by Yoo in[68],in which local distributed consensus controller were designed for the consensus tracking problem of model(15).The graphbased error surfaces for the distributed dynamic surface design were used to guarantee the consensus tracking between the followers and one leader.The function approximation technique using neural networks was employed to compensate the unknown nonlinearities unmatched in the control input of followers.The design procedure on theith follower containsnisteps.

Compared to the model of(15),the following high-order uncertain nonlinear multi-agent systems are more general

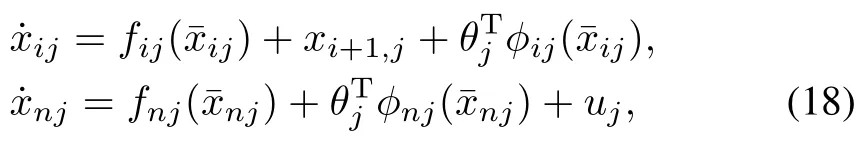
whereThe functionsfij∈R andφij∈Rpare smooth and assumed to be known.θj∈Rpjis an unknown constant vector.uj∈R is the control input of thejth system.

Ifθj=θ,distributed adaptive consensus algorithms can be proposed with the aid of backstepping technique for multiplen-order nonlinear systems in the strict feedback form.Dong[69]considered the consensus problem of model(18)by using backstepping technique and adaptive control theory,in which the order of each system is only three.If the order of systems is larger than three,the proposed procedure does not work.For the reason that,as is well known,backstepping is a recursive design procedure whose complexity increases drastically with the order of the systems.Adding a power integrator design approach is an useful method to deal with some high-order lower-triangular system problems[70−73].However,the approach has very strict conditions for use.And the main existing results are limited in single system.At present,it remains a challenging problem to design an appropriate local controller for(18).

B.Coordination of High-order Nonlinear Systems in the Brunovsky Form

Another typical high-order nonlinear multi-agent systems are described as the Brunovsky form.Each agent is modeled by a higher-order integrator incorporating unknown nonlinear dynamics and an unknown disturbance as follows

fori=1,···,n−1,wherexij∈R is theith state of agentj;xj=[x1j,···,xnj]Tis the state vector of agentj;fj(·):Rn→R is locally Lipschitz in Rnwithfj(0)=0,and it is assumed to be unknown;uj∈R is the control input;andζj∈R is an external disturbance,which is unknown but bounded.

Zhang et al.[35]developed a practical design method for cooperative tracking control of(19)with a dynamic leader.The communication network is a weighted directed graph with a fixed topology.The leader node is modeled as a higherorder nonautonomous nonlinear system.It acts as a command generator giving commands only to a small portion of the networked group.A robust adaptive neural network controller was designed for each follower node such that all follower nodes ultimately synchronize to the leader node with bounded residual errors.Fewer assumptions were made in that paper and the requirement of graph topology is relaxed such that the augmented graph has a spanning tree.This means the original graph may be disconnected,as long as the leader node pins into the proper nodes in each disconnected component.This is a necessary condition and is less stringent than strong connectedness.

Most of the consensus algorithms available in the literature are applicable to asymptotic consensus.Asymptotic consensus implies that the differences between agents states converge to zero as time goes to infinity.In many time critical applications,it is required that consensus should be reached in a finite time.Khoo et al.[74−75]introduced a set of sliding variables for multi-agent networks with both directed and undirected network topologies as

whereQi=pi/qi,withpiandqibeing odd positive integers satisfying 1＞p1/q1＞···＞pn/qn＞0.represents the virtual control law of agenthwithxh1d=0 and

wherebhdenotes the connection weight between agenthand the leader(agent 0).If agenthis connected to the leader,thenbh＞0 andbh=0 otherwise.And high-order leader-follower consensus can be guaranteed on these sliding surfaces.The fast finite-time control Lyapunov functions for control design were employed in[74−75]so that faster finite time convergence of the sliding variables could be obtained,and the design of nonsmooth control laws ensured the fast finite-time reachability of this set of sliding surfaces,which also implies fast finite-time consensus of multi-agent network.This method combines backstepping technique,sliding mode control and adding a power integrator approach.

C.Coordination of High-order Nonholonomic Systems

A nonholonomic system in physics and mathematics is a system whose state depends on the path taken to achieve it.Such a system is described by a set of parameters subject to differential constraints,such that when the system evolves along a path in its parameter space(the parameters varying continuously in values)but finally returns to the original set of values at the start of the path,the system itself may not have returned to its original state.

Many mechanical devices are described by systems with underactuation.Therefore,it is important to develop appropriate consensus algorithms for underactuated systems.Nonholonomic mobile robots are typical underactuated systems which have been studied for many years[76−81].However,most of the existing literature only focus on the basic and simple nonholonomic wheeled mobile robots which move on a horizontal planes;the motion of these systems is described by

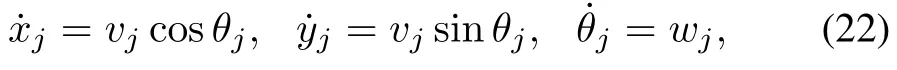
where(xj,yj)is the position of robotjin a coordinate system,θjis the orientation of robotj,vjis the speed of robotj,andwjis the angular velocity of robotj.The control signals arevjandwj.

Consider a class of high-order nonholonomic systems in the following power chained form:

wherexj=(x0j,x1j,···,xnj)T∈Rnanduj=(u0j,u1j)T∈R2represent thejth system states and control input,respectively,pi,i=0,···,n,andqk,k=1,···,n−1,are positive integers.

The system(23)under consideration represents a class of inherent nonlinear systems and includes the well-studied chained-form nonholonomic system as its special case.The main difficulty of controlling this type of nonlinear systems lies in that the systems are neither stabilizable by any timeinvariant continuous state feedback(as Brocketts necessary condition fails to be satisfied)nor affine in the control inputs,and each system only has its local information.

Lin[82]addressed the problems of almost asymptotic stabilization and global asymptotic regulation for the single system of(23),by using adding a power integrator technique.The nonholonomic system considered in[82]is not necessarily affine in the control variables and therefore cannot be handled by existing methods.Sufficient conditions are presented under which a discontinuous state feedback control law(respectively,a switching controller)can be recursively constructed.Today,it is still an open question.

D.Remarks

In terms of the inherent nonlinear characteristics of many practical multi-agent systems,Liu et al.[83]discussed consensus problems for multi-agent systems with inherent nonlinear dynamics under directed topologies.A variable transformation method is used to convert the consensus problem to a partial stability problem.Both first-order and second-order systems are investigated under fixed and switching topologies,respectively.It is assumed that the inherent nonlinear terms satisfy the Lipshitz condition.Sufficient conditions on the feedback gains are given based on a Lyapunov function method.For f i rst-order systems under a fixed topology,the consensus is achieved if the feedback gain related to the agents′positions is large enough.

If the nonlinear system satisfies the controllable and involutive conditions,then there exists the diffeomorphism.The nonlinear system can be transformed into the form of high-order integrator by feedback linearization.Therefore,the high order linear consensus algorithm can be used to achieve consensus of the nonlinear systems that is feedback linearized.By satisfying the conditions that is related with network structure and gains of the consensus algorithm,the consensus of nonlinear systems is achieved through feedback linearziation and the linear consensus algorithm.In terms of feedback linearization for consensus of nonlinear multiagent systems,Lee[84]considered the consensus of high-order nonlinear systems which can be described as

whereAisl×l,Bisl×p,the pair(A,B)is controllable,functionsα:Rl→Rpandγ:Rl→Rp×pare defined in domainD∈Rlthat contains the origin,and the matrixγ(x)is nonsingular for everyx∈D.It can be linearized by nonlinearity cancellation.A nonlinear termα(x)can be cancelled by subtraction,the controluand the nonlinearityα(x)must always appear together as a sum ofu+α(x).To cancel a nonlinear termγ(x)by division,the control u and the nonlinearityγ(x)must always appear as a product ofγ(x)u.If matrixγ(x)is nonsingular in the domain of interest,then it can be cancelled byu=β(x)v,whereβ(x)=γ−1(x)is the inverse matrixγ(x).Therefore,the nonlinear system(24)can be converted into(12)via the state feedback linearization.Then,the cooperative control results for high-order LTI systems can be used in high-order linear systems.Chen et al.[85]considered optimal full state feedback tracking control of unknown nonlinear systems.To deal with the unknown nonlinearities in the system,small learning regions are assigned online along the system trajectory in a manner dictated by a Lyapunov based self-organization method.In each of these regions,a local affine approximation is developed.A state observer-based approach adapts to the approximator parameters.With the aid of this state observer,analytic optimal controllers are proposed by solving corresponding linear quadratic control problems in each learning region.

V.DISCUSSION

Most previous studies on multi-agent systems studied the f i rst-order and second-order dynamics.However,in engineering,many systems cannot be modeled by simple dynamics but high-order ones.Thus,coordination of high-order multiagent systems has been a new heated topic recently.In most instances,the extension of cooperative control to high-order dynamics is not straightforward from the existing results with the first-order and second-order dynamics.In this paper,we review the main research and progress in distributed highorder linear and nonlinear multi-agent coordination,including the main kinds of models,cooperative control problems and approaches for high-order multi-agent systems.

Firstly,as for the high-order multi-agent systems,most of the existing literature are only concerned with the integrators chained systems with linear strict-feedback form.Due to the inherent characteristics of multiple linear systems,matrix theory approaches are used frequently in stability analysis.And the other techniques for stability analysis include dissipativity theory,nonsmooth analysis,eigenvalues analysis,backstepping technique,reduced-order observer control and especially Lyapunove functions etc.What is more,in many practical applications,the dynamics of the systems are usually not only nonlinear but also with uncertainties,thus solving consensus problems for multiple high-order uncertain nonlinear systems would make great sense for practical applications.Matrix theory approaches mentioned above are not applicable to many scenarios,especially for nonlinear systems.As the complexity of the nonlinear systems,it can not use a uni fied approach to deal with all the control problems.Thus,the cooperative control of high-order nonlinear systems with uncertainties is more challenging than that of the certain high-order linear ones.

Although the existing theoretical research and experiments have solved a number of technical problems in distributed high-order multi-agent coordination,there are still important and challenging research problems deserving further investigation.So far,the high-order multi-agent coordination and control are more a theoretical study,which needs to consider more physical truths.For example,the actual mechanical systems often have symmetry and nonholonomic constraints,etc.,in terms of satellite or spacecraft formation,it is necessary to consider its orbit constraints and drift.The high-order multi-agent theoretical results combining practical engineering approach also requires in-depth study and exploration.How to closely integrate the high-order multi-agent theory and engineering practice is still a challenging direction.

REFERENCES

[1]Reynolds C.Flocks,herds,and schools:a distributed behavioral model.ACM Siggraph Computer Graphics,1987,21(4):25−34

[2]Vicsek T,Cziro´k A,Ben-Jacob E,Cohen I,Shochet O.Novel type of phase transition in a system of self-driven particles.Physical Review Letters,1995,75(6):1226−1229

[3]Lynch N A.Distributed Algorithms.San Francisco,CA:Morgan Kaufmann,1996

[4]Balch T,Arkin R C.Behavior-based formation control for multirobot teams.IEEE Transactions on Robotics and Automation,1998,14(6):926−939

[5]Beard R W,McLain T W,Goodrich M,Anderson E P.Coordinated target assignment and intercept for unmanned air vehicles.IEEE Transactions on Robotics and Automation,2002,18(6):911−922

[6]Leonard N E,Fiorelli E.Virtual leaders,arti ficial potentials and coordinated control of groups.In:Proceedings of the 40th IEEE Conference on Decision and Control.Orlando,FL,USA:IEEE,2001.2968−2973

[7]Feddema J T,Lewis C,Schoenwald D A.Decentralized control of cooperative robotic vehicles:theory and application.IEEE Transactions on Robotics and Automation,2002,18(5):852−864

[8]Belta C,Kumar B V.Abstraction and control for groups of robots.IEEETransactions on Robotics,2004,20(5):865−875

[9]Fahimi F.Sliding-mode formation control for underactuated surface vessels.IEEE Transactions on Robotics,2007,23(3):617−622

[10]Olfati-Saber R,Murray R M.Distributed cooperative control of multiple vehicle formations using structural potential functions.In:Proceedings of the 50th IFAC World Congress.Barcelona,Spain:International Federation of Automatic Control,2002.346−352

[11]Wang X H,Yadav V,Balakrishnan S N.Cooperative UAV formation f l ying with obstacle/collision avoidance.IEEE Transactions on Control Systems Technology,2007,15(4):672−679

[12]Stilwell D J,Bishop B E.Platoons of underwater vehicles.IEEE Control Systems Magazine,2000,20(6):45−52

[13]Olfati-Saber R,Shamma J S.Consensus filters for sensor networks and distributed sensor fusion.In:Proceedings of the 44th IEEE Conference on Decision and Control,and the European Control Conference.Seville,Spain:IEEE,2005.6698−6703

[14]Cort´es J.Distributed algorithms for reaching consensus on general functions.Automatica,2008,44(3):726−737

[15]Stilwell D J,Bishop B E.Platoons of underwater vehicles.IEEE Control Systems Magazine,2000,20(6):45−52

[16]Beard R W,Lawton J,Hadaegh F Y.A coordination architecture for spacecraft formation control.IEEE Transactions on Control Systems Technology,2001,9(6):777−790

[17]Lawton J R,Beard R W.Synchronized multiple spacecraft rotations.Automatica,2002,38(8):1359−1364

[18]Ren W,Beard R W,Atkins E M.Information consensus in multivehicle cooperative control.IEEE Control Systems Technology,2007,27(2):71−82

[19]Murray R M.Recent research in cooperative control of multivehicle systems.Journal of Dynamic Systems,Measurement,and Control,2007,129(5):571−583

[20]Olfati-Saber R,Fax J A,Murray R M.Consensus and cooperation in networked multi-agent systems.Proceedings of the IEEE,2007,95(1):215−233

[21]Chebotarev P Y,Agaev R P.Coordination in multiagent systems and Laplacian spectra of digraphs.Automation and Remote Control,2009,70(3):469−483

[22]Cao Y C,Yu W W,Ren W,Chen G R.An overview of recent progress in the study of distributed multi-agent coordination.IEEE Transactions on Industrial Informatics,2013,9(1):427−438

[23]Olfati-Saber R,Murray R M.Consensus problems in networks of agents with switching topology and time-delays.IEEE Transactions on Automatic Control,2004,49(9):1520−1533

[24]Ren W,Beard R W,Atkins E M.Information consensus in multivehicle cooperative control.IEEE Control Systems Magazine,2007,27(2):71−82

[25]Min Hai-Bo,Liu Yuan,Wang Shi-Cheng,Sun Fu-Chun.An overview on coordination control problem of multi-agent system.ActaAutomatica Sinica,2012,38(10):1557−1570(in Chinese)

[26]Wu C W.Synchronization in Complex Networks of Nonlinear Dynamical Systems.Singapore:World Scientific,2007

[27]Shamma J S.Cooperative Control of Distributed Multi-Agent Systems.Hoboken,NJ:John Wiley&Sons,2008

[28]Ren W,Beard R W.Distributed Consensus in Multi-vehicle Cooperative Control:Theory and Applications.London,UK:Springer-Verlag,2008

[29]Bullo F,Cort´es J.Mart´ınez S.Distributed Control of Robotic Networks:a Mathematical Approach to Motion Coordination Algorithms.Princeton,NJ:Princeton University Press,2009

[30]Qu Z.Cooperative Control of Dynamical Systems:Applications to Autonomous Vehicles.London,UK:Springer-Verlag,2009

[31]Ren W,Cao Y C.Distributed Coordination of Multi-Agent Networks:Emergent Problems,Models,and Issues.London,UK:Springer-Verlag,2011

[32]Bai H,Arcak M,Wen J.Cooperative Control Design:A Systematic,Passivity-Based Approach.New York:Springer-Verlag,2011

[33]Mesbahi M,Egerstedt M.Graph Theoretic Methods in Multiagent Networks.Princeton,NJ,USA:Princeton University Press,2010

[34]Ren W,Moore K,Chen Y Q.High-order consensus algorithms in cooperative vehicle systems.In:Proceedings of the 2006 IEEE International Conference on Networking,Sensing and Control.Ft.Lauderdale,FL,USA:IEEE,2006.457−462

[35]Zhang H W,Lewis F L.Adaptive cooperative tracking control of higherorder nonlinear systems with unknown dynamics.Automatica,2012,48(7):1432−1439

[36]Khalil H K.Nonlinear Systems(3rd edition).Upper Saddle River,NJ,USA:Prentice Hall,2002

[37]Ren W,Moore K L,Chen Y Q.High-order and model reference consensus algorithms in cooperative control of multi-vehicle systems.ASME Journal of Dynamic Systems,Measurement,and Control,2007,129(5):678−688

[38]Jiang F C,Wang L.Consensus seeking of high-order dynamic multiagent systems with fixed and switching topologies.International Journal of Control,2010,83(2):404−420

[39]Yang T,Jin Y H,Wang W,Shi Y J.Consensus of high-order continuoustime multi-agent systems with time-delays and switching topologies.Chinese Physics B,2010,20(2):0205111−0205116

[40]Zhang W,Zeng D,Qu S.Dynamic feedback consensus control of a class of high-order multi-agent systems.IET Control Theory&Applications,2010,4(10):2219−2222

[41]He W,Cao J.Consensus control for high-order multi-agent systems.IET Control Theory&Applications,2011,5(1):231−238

[42]Miao G Y,Xun S Y,Zou Y.Consent ability for high-order multi-agent systems under noise environment and time delays.Journal of the Franklin Institute,2013,350(2):244−257

[43]Huang J,Fang H,Chen J,Dou L H,Yang Q K.On consensus of multiple high-order uncertain nonlinear systems.In:Proceedings of the 32nd Chinese Control Conference.Xi’an,China,2013.7145−7149

[44]Mo L,Jia Y M.H∞consensus control of a class of high-order multiagent systems.IET Control Theory&Applications,2011,5(1):247−253[45]Lin P,Jia Y M,Li L.Distributed robustH∞consensus control in directed networks of agents with time-delay.Systems&Control Letters,2008,57(8):643−653

[46]Lin P,Jia Y M.RobustH∞consensus analysis of a class of secondorder multi-agent systems with uncertainty.IET Control Theory&Applications,2010,4(3):487−498

[47]Liu Y,Jia Y M.Consensus problem of high-order multi-agent systems with external disturbances:anH∞analysis approach.International Journal of Robust and Nonlinear Control,2010,20(14):1579−1593

[48]Jia Y M,Cui Y.L2-L∞consensus control for high-order multi-agent systems with switching topologies and time-varying delays.IET Control Theory&Applications,2012,6(12):1933−1940

[49]Lin P,Li Z,Jia Y M,Sun M.High-order multi-agent consensus with dynamically changing topologies and time-delays.IET Control Theory&Applications,2011,5(8):976−981

[50]Xu X L,Chen S Y,Huang W,Gao L X.Leader-following consensus of discrete-time multi-agent systems with observer-based protocols.Neurocomputing,2013,118:334−341

[51]Tuna S E.Synchronizing linear systems via partial-state coupling.Automatica,2008,44(8):2179−2184

[52]Scardovi L,Sepulchre R.Synchronization in networks of identical linear systems.Automatica,2009,45(11):2557−2562

[53]Tuna S E.Conditions for synchronizability in arrays of coupled linear systems.IEEE Transactions on Automatic Control,2009,54(10):2416−2420

[54]Seo J H,Shima H,Back J.Consensus of high-order linear systems using dynamic output feedback compensator:low gain approach.Automatica,2009,45(11):2659−2664

[55]Li Z K,Liu X D,Lin P,Ren W.Consensus of linear multi-agent systems with reduced-order observer-based protocols.Systems&Control Letters,2011,60(7):510−516

[56]Wieland P,Kim J S,Allg¨ower F.On topology and dynamics of consensus among linear high-order agents.International Journal of Systems Science,2011,42(10):1831−1842

[57]Jiang F C,Wang L.Consensus seeking of high-order dynamic multiagent systems with fixed and switching topologies.International Journal of Control,2010,83(2):404−420

[58]Zeng Li,Hu Guang-Da.Consensus of linear multi-agent systems with communication and input delays.Acta Automatica Sinica,2013,39(7):1133−1140(in Chinese)

[59]Tang Yu-Tao,Hong Yi-Guang.Hierarchical distributed control design for multi-agent systems using approximate simulation.Acta Automatica Sinica,2013,39(6):868−874(in Chinese)

[60]Wang J H,Liu Z X,Hu X M.Consensus of high order linear multiagent systems using output error feedback.In:Proceedings of the 48th IEEE Conference on Decision and Control,2009 Held Jointly with the 2009 28th Chinese Control Conference.Shanghai,China:IEEE,2009.3685−3690

[61]Xi J X,Cai N,Zhong Y S.Consensus problems for high-order linear time-invariant swarm systems.Physica A:Statistical Mechanics and Its Applications,2010,389(24):5619−5627

[62]Cai N,Xi J X,Zhong Y S.Swarm stability of high-order linear timeinvariant swarm systems.IET Control Theory&Applications,2011,5(2):402−408

[63]Xi J X,Shi Z Y,Zhong Y S.Consensus analysis and design for highorder linear swarm systems with time-varying delays.Physica A:Statistical Mechanics and Its Applications,2011,390(23−24):4114−4123

[64]Xi J X,Shi Z Y,Zhong Y S.Output consensus analysis and design for high-order linear swarm systems:partial stability method.Automatica,2012,48(9):2335−2343

[65]Ding L,Han Q L,Guo G.Network-based leader-following consensus for distributed multi-agent systems.Automatica,2013,49(7):2281−2286

[66]Dong W J,Ben Ghalia M,Farrell J A.Tracking control of multiple nonlinear systems via information interchange.In:Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference.Orlando,FL,USA:2011.5076−5081

[67]Dong W J.Adaptive consensus seeking of multiple nonlinear systems.International Journal of Adaptive Control and Signal Processing,2012,26(5):419−434

[68]Yoo S J.Distributed consensus tracking for multiple uncertain nonlinear strict-feedback systems under a directed graph.IEEE Transactions on Neural Networks and Learning Systems,2013,24(4):666−672

[69]Dong W J.On consensus of multiple uncertain nonlinear systems.In:Proceedings of the 7th IEEE Sensor Array and Multichannel Signal Processing Workshop.Hoboken,NJ,USA:IEEE,2012.385−388

[70]Qian C J,Lin W.Non-Lipschitz continuous stabilizers for nonlinear systems with uncontrollable unstable linearization.Systems&Control Letters,2001,42(3):185−200

[71]Lin W,Qian C J.Adding one power integrator:a tool for global stabilization of high-order lower-triangular systems.Systems&Control Letters,2000,39(5):339−351

[72]Lin W,Qian C J.Adaptive control of nonlinearly parameterized systems:a nonsmooth feedback framework.IEEE Transactions on Automatic Control,2002,47(5):757−774

[73]Huang X Q,Lin W,Yang B.Global finite-time stabilization of a class of uncertain nonlinear systems.Automatica,2005,41(5):881−888

[74]Khoo S,Xie L H,Zhao S K,Man Z H.Multi-surface sliding control for fast finite-time leader-follower consensus with high order SISO uncertain nonlinear agents.International Journal of Robust and Nonlinear Control,doi:10.1002/rnc.2997

[75]Khoo S,Trinh H M,Man Z H,Shen W X.Fast finite-time consensus of a class of high-order uncertain nonlinear systems.In:Proceedings of the 5th IEEE Conference on Industrial Electronics and Applications.Taichung,China:IEEE,2010.2076−2081

[76]Dimarogonas D V,Kyriakopoulos K J.On the rendezvous problem for multiple nonholonomic agents.IEEE Transactions on Automatic Control,2007,52(5):916−922

[77]Dong W J,Farrell J A.Cooperative control of multiple nonholonomic mobile agents.IEEE Transactions on Automatic Control,2008,53(6):1434−1448

[78]Dong W J,Farrell J A.Decentralized cooperative control of multiple nonholonomic dynamic systems with uncertainty.Automatica,2009,45(3):706−710

[79]Dong W J.Distributed observer-based cooperative control of multiple nonholonomic mobile agents.International Journal of Systems Science,2012,43(5):797−808

[80]Zhang Q,Lapierre L,Xiang X B.Distributed control of coordinated path tracking for networked nonholonomic mobile vehicles.IEEE Transactions on Industrial Informatics,2013,9(1):472−484

[81]Murray R M,Sastry S S.Nonholonomic motion planning:steering using sinusoids.IEEE Transactions on Automatic Control,1993,38(5):700−716

[82]Lin W,Pongvuthithum P,Qian C J.Control of high-order nonholonomic systems in power chained form using discontinuous feedback.IEEE Transactions on Automatic Control,2002,47(1):108−115

[83]Liu K E,Xie G M,Ren W,Wang L.Consensus for multi-agent systems with inherent nonlinear dynamics under directed topologies.Systems&Control Letters,2013,62(2):152−162

[84]Lee T,Ahn H S.Consensus of nonlinear system using feedback linearization.In:Proceedings of the 2010 IEEE/ASME International Conference on Mechatronics and Embedded Systems and Applications.Qingdao,China:IEEE,2010.26−31

[85]Chen Y M,Dong W J,Farrell J A.Self-organized locally linear optimal tracking control for unknown nonlinear systems.In:Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference.Orlando,FL,USA:IEEE,2011.5401−5406