Leader-following Rendezvous with Connectivity Preservation of Single-integrator Multi-agent Systems

Yi DongJie Huang

I.INTRODUCTION

MAINTAINING connectivity in a multi-agent system is necessary in such problems as rendezvous, flocking,swarming and so on.These problems have been studied for both single-integrator multi-agent systems[1−6]and doubleintegrator multi-agent systems[2,7−8].There are two types of rendezvous problems,namely leaderless rendezvous problem and leader-following rendezvous problem.While the leaderless rendezvous problem requires that the outputs of all agents asymptotically approach a same location,the leader-following rendezvous problem further requires that the outputs of all agents approach a given trajectory asymptotically.So far,the study of the problem of rendezvous with connectivity preservation is mainly focused on the leaderless case[1,3−6]with a few exceptions where the problem of leader-following rendezvous with connectivity preservation is studied[2,7−8].Reference[2]studied the leader following rendezvous with connectivity preservation for both single-integrator and double-integrator systems using a discontinuous control law.Reference[8]studied the leader-following rendezvous with connectivity preservation for double-integrator systems where the leader was also a double integrator system.Reference[7]also studied the leader following rendezvous with connectivity preservation for double-integrator systems under a class of leader systems including double-integrator and harmonic systems.

In this paper,we will consider the problem of leader following rendezvous with connectivity preservation of singleintegrator multi-agent systems.In comparison with[2],we employ a continuous control law,and our control law does not need to know the upper bound of the derivative of the leader signal.

The problem formulation in this paper is,in spirit,similar to that of[7].However,the approach of this paper is different from that of[7]in that our control law does not contain a distributed observer,and is thus much simpler than the one in[7].We also need to establish lemma to lay the foundation of the main result of the current paper.

The rest of this paper is organized as follows.In Section II,we give a precise formulation of the problem of leader-following rendezvous with connectivity preservation for single-integrator multi-agent systems.In Section III,we present our main result.An example is presented in Section IV.Some concluding remarks are given in Section V.Finally,we note that a preliminary version of this paper appears in[9].

II.PROBLEM FORMULATION

Consider a group of single-integrator systems:

wherexi∈Rnandui∈Rnare the state and the input of agenti.Also consider an autonomous linear system

wherex0∈RnandSis a constant matrix.

The system composed of(1)and(2)can be viewed as a multi-agent system of(N+1)agents with(2)as the leader and theNsubsystems of(1)as theNfollowers.With respect to the system composed of(1)and(2),we can define a digraph1See appendix for a self-contained summary of digraph.wherewith 0 associated with the leader system andi=1,···,N,associated with theith subsystem of(1),and.The setis called the node set of(t)and the setis called the edge set of.We use the notationto denote the neighbor set of nodeifori=0,1,···,N.The definition ofassociated with the system composed of(1)and(2)is as follows.

Given anyr＞0 and∈∈(0,r),for anyt≥0,=is defined such that:

1);

2)if,then;

3),fori=0,1,···,N;

4)for,ifand,then

5)for,ifand,then

Remark 1.The definition here is the same as that in[7].If∈=0,then the above definition is similar to that given in[5].Thus the physical interpretation ofris the sensing radius of the distance sensor of each follower.The number∈is to introduce the effect of hysteresis.It is noted that the leader does not have a control and,therefore,there is no edge from a follower to the leader.

We will consider the following distributed state feedback control law

wherehiis a suf ficiently smooth function to be speci fied later.

The control law(3)is called a distributed state feedback control law because,at any time instantt,the controluican takexj,j/=i,for feedback control if and only if nodejis a neighbor of nodei.

Define a subgraphofwhereV={1,···,N},andE(t)⊆V×Vis obtained fromby removing all edges from node 0 to the nodes inV.Clearly,G(t)is an undirected graph.Fori=1,···,N,let.It can be seen that fori=1,···,N,Ni(t)is the neighbor set of nodeiwith respect toG(t).

The problem of leader-following rendezvous with connectivity preservation is described as follows.

Definition 1.Given the multi-agent system composed of(1)and(2), find a control law of form(3)such that for all initial conditionsxi(0),i=0,1,···,N,that makeconnected,the closed-loop system has the following properties:

1)is connected for allt≥0;

2)limt→∞(xi−x0)=0,i=1,···,N.

Remark 2.The problem of leader-following rendezvous with connectivity preservation defined here is similar to the leader-following problem of rendezvous with connectivity preservation defined for double-integrator system in[7].

III.MAIN RESULT

Like in[7−8],we will adopt the potential function approach to design our control law.Thus,we will first introduce a bounded potential function introduced in[8]as follows

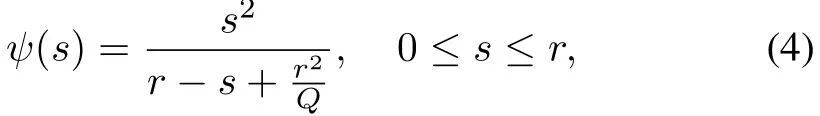
whereQis some positive number.The functionψis nonnegative and bounded over[0,r],and its derivative=is positive for alls∈(0,r].Moreover,it is shown in[9]that the function has the property that for anyα＞0,andβ≥0,any∈∈(0,r),if,then

Now we are ready to propose our distributed state feedback control law as follows:

whereγis a suf ficiently large positive number and

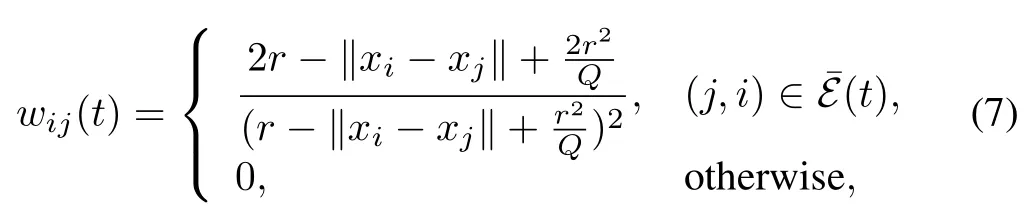
withi=1,···,N,j=0,1,···,N,i/=j.

Letfor 0≤s≤r.Then=φ(0)≤φ(s)≤overs∈[0,r].Letand.Then,for all,0＜a≤wij(t)≤b.Let,i=0,1,···,N.Then,in terms of,the closed-loop system is

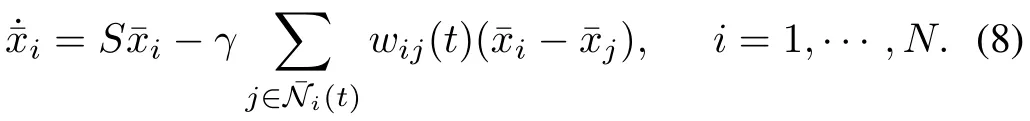
Let.Then the closed-loop system can be put in the following compact form

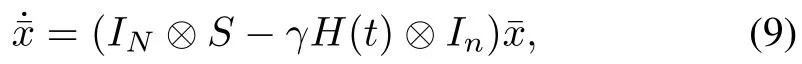
wherewithβi=,i=1,···,N.

Before presenting our main result,we will establish the following lemma.

Lemma 1.Assume graphis connected for allt≥0,andwhenevert2≥t1≥0.Then

1)There exist constant positive definite matricesH1andH2such that 0＜H1≤H(t)≤H2for allt≥0;

2)LetwhereλM(H)andλm(H)are the largest and smallest eigenvalues of a positive definite matrixHandδ≥0.Then,for allγ＞γ0,＞0 andfor allt≥0.

Proof.1)Letbe any connected graph such that0⊂(0).Let

where

and,i=1,···,N,and let

Note thatH1=−M1+∆1,whereM1is a constant Metzler matrix with zero row sum whose nonzero off-diagonal entries are equal toa,and∆1is a nonnegative diagonal matrix with at least one positive diagonal entry.It can be seen that Γ(M1)=G0,whereG0is the subgraph ofobtained fromby removing node 0 and all edges adjacent to node 0.By Remark A1,H1is positive definite.

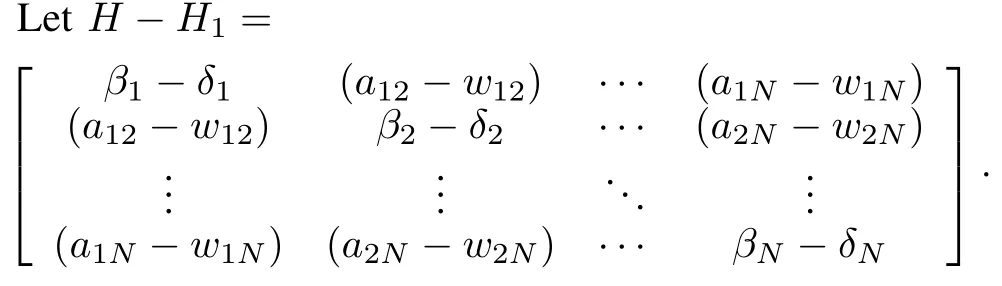
Since fori=1,···,N,≥≥0,H−H1is positive semi-definite by Gersgorin Theorem.

Next,letH2−H=

Then,fori=1,···,N,Thus,H2−His positive semi-definite by Gersgorin theorem.Thus we have 0＜H1≤H(t)≤H2for allt≥0.

2)Letλi(t)andαi(t),i=1,···,N,be the eigenvalues and the eigenvectors ofH(t),respectively.Letei,i=1,···,n,be theith column ofIn.Then it can be veri fied that fori=1,···,N,j=1,···,n,(γH2(t)⊗In−and(αi⊗ej)are linearly independent.Thus,the eigenvalues of belong to the setwhich has a lower boundsinceH1≤H(t)≤H2.For alltherefore for all□

Now we present our main result.

Theorem 1.Given anyr＞0 and∈∈(0,r),the problem of leader-following rendezvous with connectivity preservation of the system composed of(1)and(2)is solvable by a control protocol of the form of(6).

Proof.Givenr＞0 and∈∈(0,r),the control law is determined by two design parametersQandγ.Letα=N(N−1)/2+N,β=0,and

Pick any finiteQsuch thatQ＞Qmax.

To determineγ,note that there are only finitely many connected graphs withNedges(an undirected edge is counted as one edge).Denote these graphs by,i=1,···,p,wherepis some positive integer.For eachwe can define a matrix,,in the same way as we defi neH1in(10).Denote the minimal eigenvalue ofby.Let.Letγ0=‖S‖λM(H2)/λ2mwhereH2is the same as defined in(12).For anyt≥0,ifis connected,there exists some 1≤i≤psuch that.Thus,by Lemma 1,for allγ＞,and for anyt≥0,γH2(t)⊗ifis connected.Fix thisγand letand.

Now we will first show that the above control law is such that graph(t)is connected for allt≥0.For this purpose,let

wherebi(t)=1 if,andbi(t)=0 otherwise.

We callVas an energy function for(9).It can be seen that for all initial conditionsxi(0),i=0,1,···,N,is connected,

From(8),we have

Then the derivative of the energy function(14)along(9)satisfies

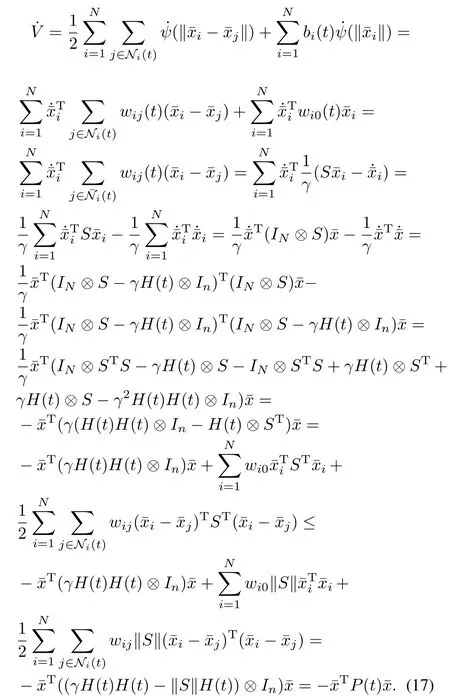
By the continuity of the solution of(9),there exists 0＜t1≤∞such thatfor allt∈[0,t1).Ift1=∞,then the graph is connected for allt≥0.Thus,P(t)≥λγINnfor allt≥0.Therefore,for allt≥0,

Then(18)implies

Ifdoes not hold for allt≥0,then there must exist some finitet1≥0 such that

We now claim.In fact,sinceis connected,our choice ofγguaranteesP(t)≥λγINnfor all 0≤t＜t1,therefore,(17)implies

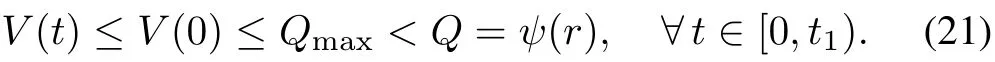
Assume,for some,.Then1,which impliesV(t1)≥Qthus contradicting(21).Thus,the graph will not lost edges at timet1.Therefore,.

Sincecan only have finitely many edges,there exists a finite integerk＞0 such that

Thus,along any trajectory of the closed-loop system,we have

Thus,

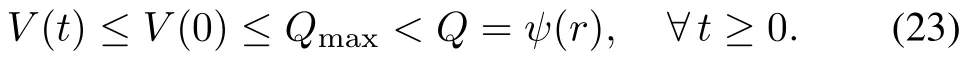
Therefore,for allt≥0,graphis connected.

Remark 3.Since we allow our leader system to be a class of autonomous linear systems of form(2),our control law relies on matrixSdefining the leader system.This feature is a reminiscence of the classical internal model design method which can be found in[11−12].It is this feature that enables a control law to track,instead of a single trajectory,but a class of trajectories.It is noted that knowing the information of the matrixSis less demanding than knowing the trajectory of the leader.For example,a sinusoidal signalAsin(ωt+φ)is defined by three parametersA,ω,andφ.The matrixSis solely defined byω.By usingSin the control law,we can handle a sinusoidal signal with frequencyω,arbitrary amplitudeA,and arbitrary initial phaseφ.In the special case where the leader signal is step function or ramp function,we simply takeS=0,or.Therefore,in these two special cases,the control law does not really depend on any parameter of the leader signal.

IV .AN EXAMPLE

Consider the multi-agent system composed of(1)and(2)withn=2 andN=4.Assume the sensing range isr=1 and∈=0.1.To obtain the design parameterQin the potential function,using(5)withα=N(N−1)/2+N=10 givesα(r−∈)2/∈=81.Then takingQ=82 makes(5)satis fied.Thus the potential function is

Chooseγ=2600 according to the method in the proof of Theorem 1.For the purpose of simulation,let the initial values of various variables be

It can be verified that these initial values are such that={(0,1),(1,2),(2,3),(3,4)},which forms a connected graph.

With these parameters,we have evaluated the performance of the control law(6)for two different leader systems.

Case 1.The leader system generates a ramp signal

In this case,

Some of the simulation results are shown in Fig.1 and Fig.2.Fig.1 shows the distances of the edges{(0,1),(1,2),(2,3),(3,4)},which constitute the initial edge set.It can be seen that the network is connected.Fig.2 further shows the time response of the state of all the followers.It can be seen that all the followers asymptotically approach the leader.

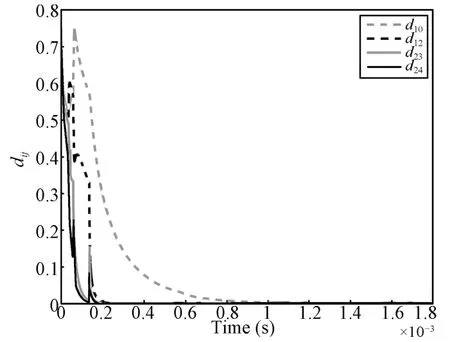
Fig.1.Distances among agents.

Case 2.The leader system generates a sinusoidal signal

In this case,

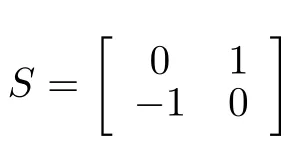
Fig.3 shows the distances of the edges{(0,1),(1,2),(2,3),(3,4)},which constitute the initial edge set.Fig.4 further shows the time response of the state of all the followers.Satisfactory performance is observed.

Fig.2.Position difference between follower and leader.

V.CONCLUSION

In this paper,we have considered the problem of leader following rendezvous with connectivity preservation for a multiple single-integrator system,where the leader system can be any linear autonomous system.We have proposed a distributed state feedback control protocol that is able to maintain the connectivity of the system,and,at the same time,achieve asymptotic tracking of all followers to the output of the leader system.

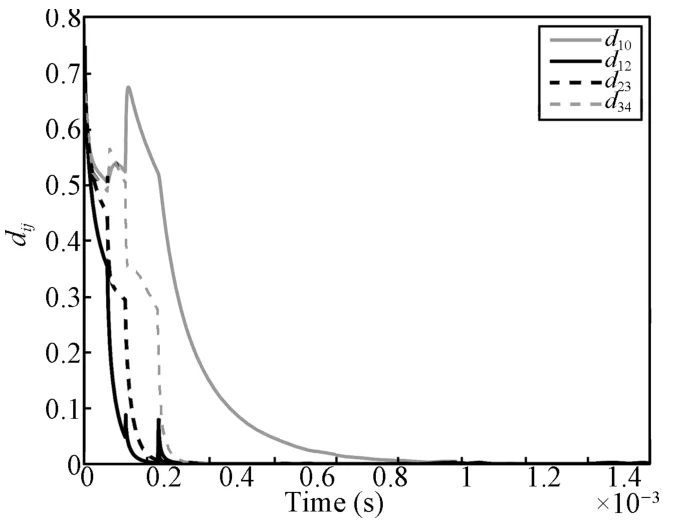
Fig.3.Distances among agents.

Fig.4.Position difference between follower and leader.

Appendix

We first introduce some graph notation,which can be found in[13].A digraphG=(V,E)consists of a finite set of nodesV={1,···,N}and of an edge setE={(i,j),i,j∈V,i/=j}.Nodeiis called a neighbor of nodejif the edge(i,j)∈E.Nidenotes the subset ofVthat consists of all the neighbors of nodei.If graphGcontains a sequence of edges of the form(i1,i2),(i2,i3),···,(ik,ik+1),then the set of{(i1,i2),(i2,i3),···,(ik,ik+1)}is called a path ofGfromi1toik+1,and nodeik+1is said to be reachable from nodei1.Edge(i,j)is called undirected if(i,j)∈Eimplies(j,i)∈E.The graph is called undirected if every edge inEis undirected.A graph is called connected if there exists a nodeisuch that any other nodes are reachable from nodei.Nodeiis called a root of the graph.DigraphGs=(Vs,Es)is a subgraph ofG=(V,E)ifVs⊆VandEs⊆E∩(Vs×Vs).

A matrixL=[lij]∈RN×Nwith zero row sum is said to be a Laplacian matrix of graphGif,fori,j=1,···,N,i/=j,lij＜0 iff⇔(j,i)∈E,andlij=ljiif(j,i)is a undirected edge ofE.Clearly,L1N=0.

Given any matrixM=[mij]∈RN×N,one can define a graph denoted by Γ(M)=(V,E)whereV={1,···,N},and andE={(i,j)|mji/=0,i/=j,i,j=1,···,N}.Clearly,ifLis any Laplacian matrix of graphG,then Γ(L)=G.A matrix ofM=[mij]N×Nwith nonnegative off-diagonal elements and zero row sums is called Metzler matrix.IfLis the Laplacian of some graphG,then−Lis a Metzler matrix.

Remark A1.It is shown in[14]that a Metzler matrix has at least one zero eigenvalue and all the nonzero eigenvalues have negative real parts.Furthermore,a Metzler matrix has exactly one zero eigenvalue and its null space is span{1}if and only if the associated graph is connected.A symmetric Metzler matrix is negative semi-definite.LetMbe a symmetric Metzler matrix whose graph is connected.Let∆=diag{a10,···,aN0},whereai0≥0 fori=1,···,N.Then for any nonzero,nonnegative diagonal matrix∆,−M+∆is positive definite.

REFERENCES

[1]Ajorlou A,Momeni A,Aghdam A.A class of bounded distributed control strategies for connectivity preservation in multi-agent systems.IEEE Transactions on Automatic Control,2010,55(12):2828−2833

[2]Cao Y C,Ren W.Distributed coordinated tracking with reduced interaction via a variable structure approach.IEEE Transactions on Automatic Control,2012,57(1):33−48

[3]Dimarogonas D V,Johansson K H.Bounded control of network connectivity in multi-agent systems.IET Control Theory and Applications,2010,4(8):1330−1338

[4]Ji M,Egerstedt M.Connectedness preserving distributed coordination control over dynamic graphs.In:Proceedings of the 2005 American Control Conference.Portland,OR,USA:IEEE,2005.93−98

[5]Ji M,Egerstedt M.Distributed coordination control of multiagent systems while preserving connectedness.IEEE Transactionson Robotics,2007,23(4):693−703

[6]Zavlanos M M,Pappas G J.Potential fields for maintaining connectivity of mobile networks.IEEE Transactions on Robotics,2007,23(4):812−816

[7]Dong Y,Huang J.A leader-following rendezvous problem of double integrator multi-agent systems.Automatica,2013,49(5):1386−1391

[8]Su H S,Wang X F,Chen G R.Rendezvous of multiple mobile agents with preserved network connectivity.Systems and Control Letters,2010,59(5):313−322

[9]Dong Y,Huang J.Leader-following rendezvous with connectivity preservation of single-integrator multi-agent systems.In:Proceedings of the 12th International Conference on Control,Automation,Robotics and Vision.Guangzhou,China:IEEE,2012.1686−1690

[10]Slotine J J,Li W P.Applied Nonlinear Control.New Jersey:Prentice Hall,1991

[11]Francis B A.The linear multivariable regulator problem.SIAM Journal on Control and Optimization,1977,15(3):486−505

[12]Huang J.Nonlinear Output Regulation:Theory and Applications.Phildelphia:SIAM,2004

[13]Godsil C,Royle G.Algebraic Graph Theory.New York:Springer-Verlag,2001

[14]Lin Z.Coupled Dynamic Systems:from Structure towards Stability and Stabilizability[Ph.D.dissertation],University of Toronto,Canada,2005