On Dynamics and Nash Equilibriums of Networked Games

Daizhan ChengTingting XuFenghua HeHongsheng Qi

I.INTRODUCTION

THE evolutionary game was firstly proposed by biologists about four decades ago.It was used in biology to model the evolution of species in nature.Later on,it had various applications not only to biology but also to economics,social sciences,etc.[1−2].In an evolutionary game there are usually many players,and the players as nodes form a complete graph.That is,each player plays with all others,and repeats the game for many or even in finite times.

Though it has been proved very useful,this approach has an obvious drawback,that is,the topology describing the relationship of players is ignored.Recently,the network[3−6]was borrowed to describe the topology of players in an evolutionary game.Roughly speaking,an evolutionary game with a graph using players as nodes is a networked evolutionary game(NEG).For the last decade or so,the networked evolutionary game has become a hot topic[7−9].Some survey papers provided a general description and overall picture for the characteristics and research topics of NEGs[10−11].

The progress of the study of NEGs is rapid and many interesting results have been reported.For instance,the evolution of cooperation on scale-free networks was investigated in[12−13],evolution on two interdependent networks was considered in[14−15],etc.We refer to[16]for some recent developments.

To the best of our knowledge,most of researches on NEGs are based on Monte Carlo and similar simulations.It can hardly be used for general,e.g.,asymmetric networks.Using semi-tensor product of matrices,this paper proposes a new framework to model the networked game.Then we present an algorithm to calculate the mixed strategy Nash equilibrium of a multi-player game.By exploring the relationship between local and global Nash equilibriums,the method is applied to static network games.Finally,a sufficient condition is provided to construct the Nash equilibrium of networked evolutionary game via the Nash equilibrium of its corresponding one step static game.

The paper is organized as follows.Section II introduces some notations and gives a brief survey on semi-tensor product of matrices.Section III analyzes the structure of networked evolutionary games.Then a rigorous mathematical model for NEGs is presented in Section IV.Section V proposes a method to calculate the Nash equilibrium for multi-player games.In Section VI,we first investigate the static Nash equilibrium of networked game.Then the relationship between local and global Nash equilibriums is revealed,and it is used to calculate the static Nash equilibrium of networked games.Finally,a sufficient condition is obtained to construct Nash equilibrium of NEG via its corresponding one step static Nash equilibriums.Section VII contains some concluding remarks.

II.PRELIMINARIES

A.Notations

1)Mm×nis the set ofm×nreal matrices.

2)Coli(M)is theith column of matrixM;Col(M)is the set of columns ofM.

3)Dk={1,2,···,k}.

4),i.e.,it is theith column of the identity matrix.

5)∆n=Col(In).

6)M∈Mm×nis called a logical matrix if Col(M)⊂∆m,the set ofm×nlogical matrices is denoted byLm×n.

7)AssumeL∈Lm×n,and

then its shorthand form is

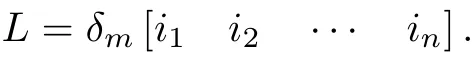
8)r=(r1,···,rk)T∈Rkis called a probabilistic vector,ifri≥0,i=1,···,k,and.

The set ofkdimensional probabilistic vectors is denoted byΥk.

9)LetR∈Mm×n.If Col(R)⊂Υm,thenRis called a probabilistic matrix.The set ofm×ndimensional probabilistic matrices is denoted byΥm×n.

B.Semi-tensor Product of Matrices

Semi-tensor product of matrices is the main tool in this paper.The following is a brief survey.

Definition 1.LetA∈Mm×nandB∈Mp×q.Denote byt=lcm(n,p)the least common multiple ofnandp.Then we define the semi-tensor product(STP)ofAandBas

Remark 1.1)Whenn=p,AB=AB.Therefore the STP is a generalization of the conventional matrix product.So symbol“”can be omitted,and the matrix product is assumed to be STP in the sequel.

2)STP keeps all the major properties of the conventional matrix product valid,including the associative law and distributive law.

We cite some basic properties which are used in this note.

Proposition 1.1)For any two matrices,

2)IfAandBare invertible,then

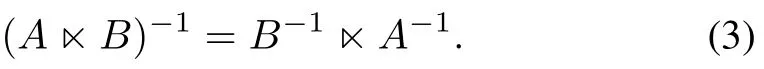
Proposition 2.LetX∈Rtbe a column vector.Then for matrixM,

Definition 2.Define a matrix

which is called a swap matrix.

Proposition 3.LetX∈RmandY∈Rnbe two column vectors.Then

Finally,we consider how to express a Boolean function into the algebraic form.

Theorem 1.Letf:Bn→Bbe a Boolean function expressed as

wherexi∈B={0,1}.Identify

Then there exists a unique logical matrixMf∈L2×2n,called the structure matrix off,such that by using(8),(7)can be expressed in the vector form as

which is called the algebraic form of(7).

Assumexi∈Dki,i=1,···,n.We identifyDk～∆kby

AssumeBy identi fication(10),fbecomes a mapping,which is called the vector form off.

Theorem 1 can be generalized as

Theorem 2.LetQUsing identi fication(10),fcan be expressed in the vector form as

whereMf∈Lk0×kis unique,which is called the structure matrix off.Moreover,(11)is called the algebraic form off.

III.STRUCTURE OFNEGS

Assume there arenplayers(or agents)denoted byN={1,2,···,n},andE⊂N×Ndescribes the relation between players.Then a network graph(N,E)is obtained.

Definition 3.1)jis said to be in the neighborhood ofi,denoted byj∈Ui,if either(i,j)∈Eor(j,i)∈E.Hence the definition of neighborhood hereafter is independent of the directions of edges,even if the graph is directed.

2)As a convention,we definei∈Ui.

3)Ifk∈Ujandj∈Ui,thenkis said to be in the subneighborhood ofi,denoted byk∈.

Definition 4.GameGis called a fundamental network game(FNG),if

1)Ghas two players;

2)Both players have the same set of strategies,denoted byS={1,2,···,k}.Gis symmetric if

Now each playeriplays the FNGGpairwisely with each of its neighborsj,j∈Ui{i}.The overall payoff ofiis the average of its payoffsci,j,precisely,

Definition 5.A strategy updating rule(SUR),denoted by Π,is a rule for each playerito update its strategyxi(t+1),based on its neighbors′information at timet.Precisely,it can be expressed as

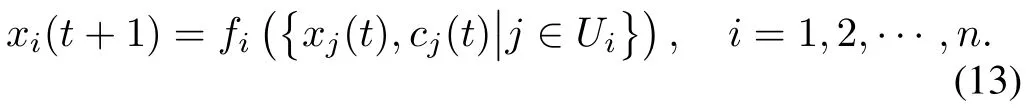
Note that thefiin(13)will be uniquely determined by the SUR.Throughout this paper we use only the following two typical SURs:

1)Π1(Unconditional imitation[8]):

The strategy of playeriat timet+1,xi(t+1),is selected as the best strategy among the strategies of its neighborsj∈U(i)at timet.Precisely,if

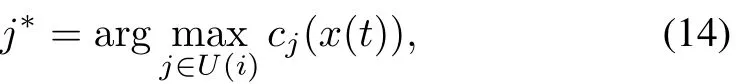
then

If the argmax set is not a singleton,say

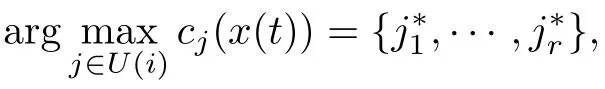
then a fixed priority is given as

This method leads to a deterministick-valued dynamics.

2)Π2(Simplified Fermi rule[17−18]):

Playerichooses randomly a neighborhoodj∈U(i)and comparescj(x(t))withci(x(t))to determinexi(t+1)as

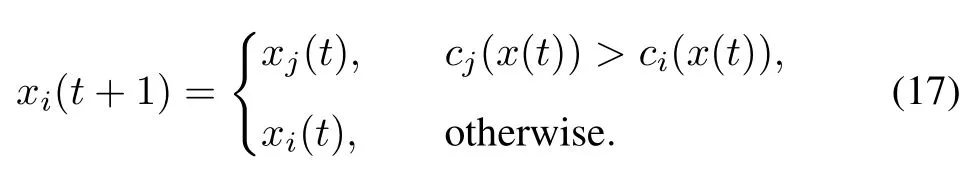
This method leads to a probabilistick-valued dynamics.

Now we are ready to give a rigorous definition of NEGs[19].

Definition 6.An NEG,denoted by a triple((N,E),G,Π),consists of three factors:1)the network graph(N,E);2)an FNGG;3)an SUR Π.

Note that a network graph could be directed,which is applicable to the case when the FNG is asymmetric.In this case(i,j)∈Emeans in the FEGiis the first player 1 andjis the second player 2.

Example 1.1)Consider a networked game described by an undirected graph in Fig.1(a).Assume the strategy setS0={1,2},and the payoff bi-matrix of the 1st FNGG1,played by player pairs(1,2)and(2,3),is shown in Table I,and the payoff bi-matrix of the 2nd FNGG2,played by(3,4),is shown in Table II.

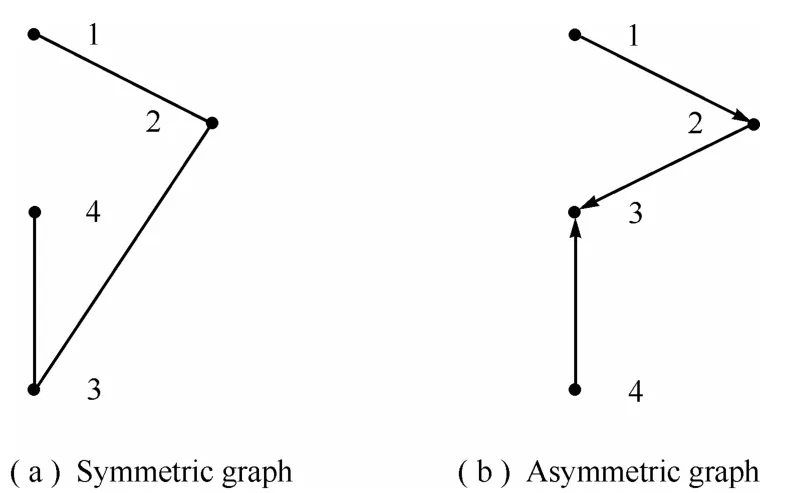
Fig.1.Two kinds of graphs.

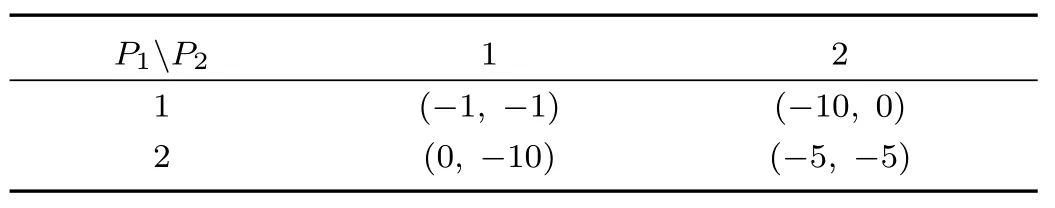
TABLE I PAYOFF BI-MATRIX FOR Fig.1(a):(1,2),(2,3)

TABLE II PAYOFF BI-MATRIX FOR Fig.1(a):(3,4)

SinceG1,G2are symmetric,this is a symmetric NEG.

2)Consider a networked game described by directed graph in Fig.1(b).AssumeS0={1,2},and the payoff bi-matrix of the unique FNGG3,played by(4,2),(2,1),(1,3),(3,2),is shown in Table III.

TABLE III ASYMMETRIC PAYOFF BI-MATRIX FOR Fig.1(b)

SinceG3is asymmetric,this is an asymmetric NEG.

This example will be further investigated in the sequel.

IV.NETWORK PROFILE DYNAMICS

From the SUR equation(2.2),sincecj(t)depends onxk(t),k∈Uj,one sees easily that(2.2)can be rewritten as

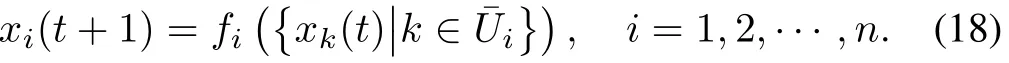
This is a standardk-valued logical dynamic network(might be a probabilistic one).If we can figure outfiin(3.1),the network pro file dynamics can be constructed via standard procedures[20].In fact,it can be determined by SUR.It will be illustrated via an example later.

According to Theorem 2,(3.1)can be expressed into the vector form as

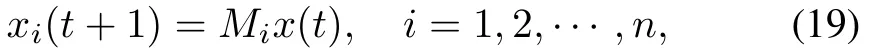
where.

Then the network pro file dynamics is obtained as

To see how to constructM,it depends on the SUR,which leads to two possible cases:

1)Case 1(deterministic model):whenMi∈Lk×kn,i=1,···,n,and

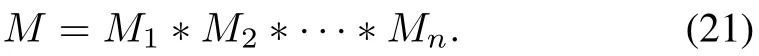
Note that in the above“∗”is the Khari-Rao product defined as follows[21]:LetA∈Mp×nandB∈Mq×n.Then

2)Case 2(probabilistic model):

whereThen(20)becomes a probabilistic model with

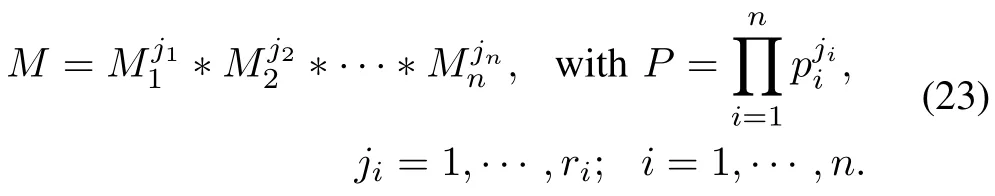
Example 2.Recall Example 1.

1)Consider part 1)in Example 1 and assume the SUR is Π1:

x1(t+1)depends on its sub-neighborhoodonly.For instance,ifx1=1,x2=2,x3=2,then using Table I,we have

Then

Similarly,all the values off1are calculated and listed in Table IV.

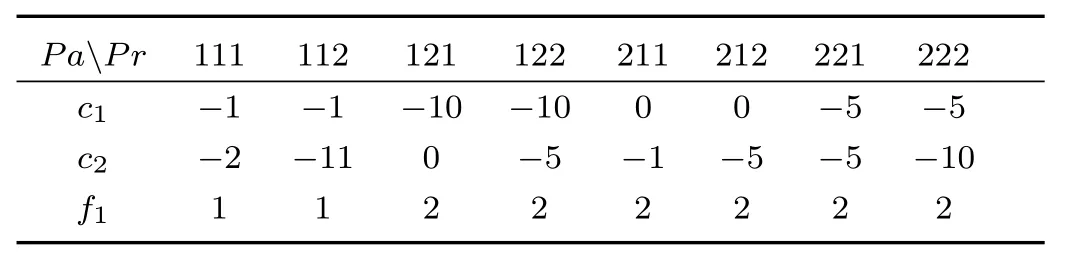
TABLE IV CALCULATING fi(Pa:PAYOFF,Pr:PROFILE)

That is,in the vector form:

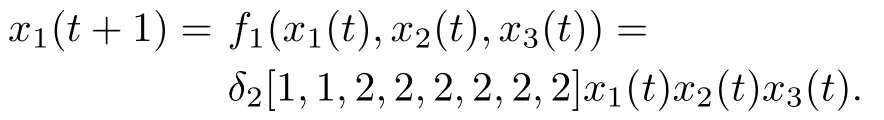
Similarly,we can obtain

and

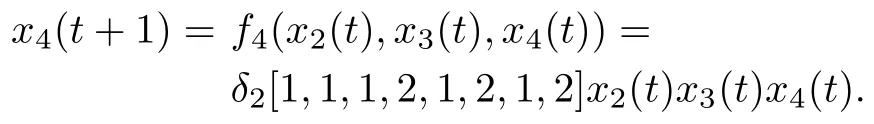
Define.Then we can express the above 4 equations as

where

Then the network pro file dynamics is

where

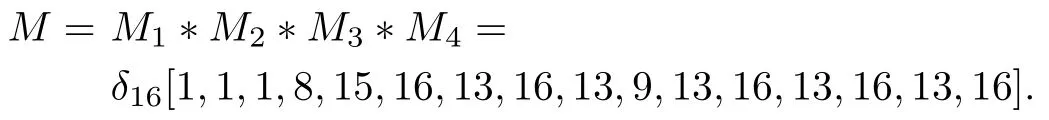
2)Consider part 2)in Example 1 and assume the SUR is Π2:

Now only players 2 and 3 have different choices.We useto describe the SUR when player 2 chooses to compete with player 1,andthe SUR when player 2 chooses player 3;we usefor the case player 3 chooses player 2 andthe case player 3 chooses player 4.Using Table III,thefi,i=1,2,3,4 can be calculated,which are shown in Table V.

It comes from Table V that

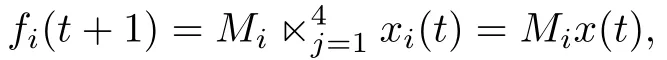
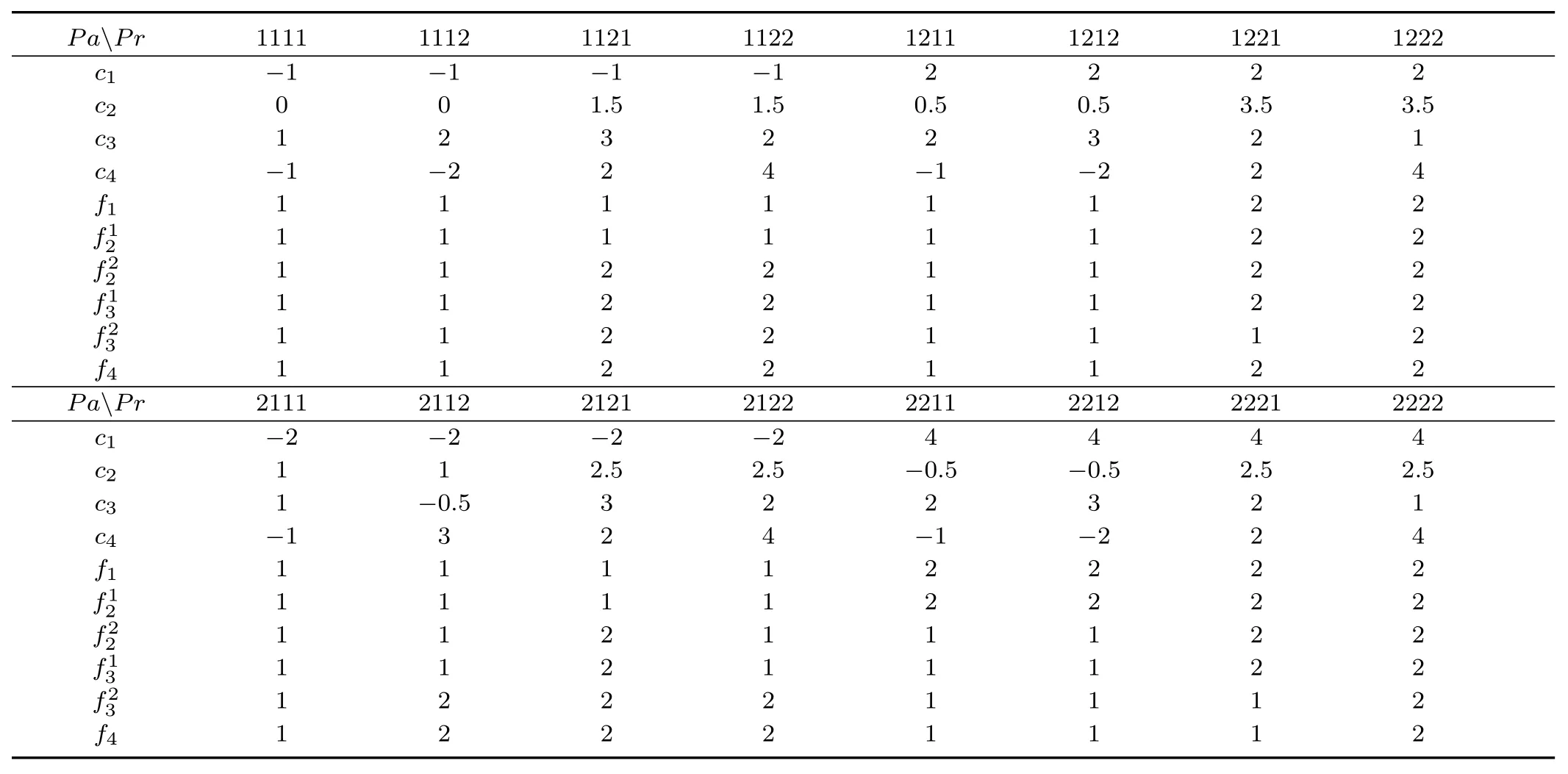
TABLE V CALCULATING fi(Pa:PAYOFF,Pr:PROFILE)

where

1)

2)

where

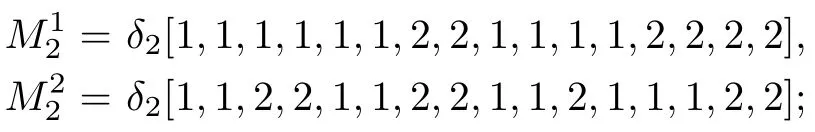
3)

where

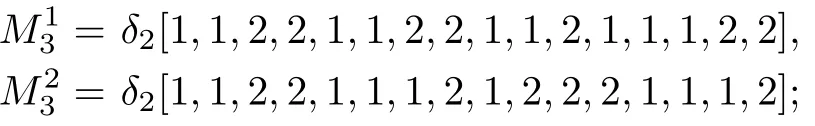
4)M4=δ2[1,1,2,2,1,1,1,2,1,2,2,2,1,1,1,2].

We conclude that the overall network pro file dynamics is

with

V.CALCULATINGNASH EQUILIBRIUM(S)

A.Equation for Nash Equilibrium(s)

First,we consider a static networked game(NG).From(12)it is clear that the payoffs arek-valued pseudo-logical functions.Then,they can be expressed into the algebraic form as

whereGi∈Rknis a row vector.

In this subsection,we mainly consider games with mixed strategies.Because the existence of Nash equilibrium is assured as the mixed strategy is allowed[22−23].

The following lemma comes from definitions immediately.

Lemma 1.Consider the payoffs in algebraic form as(27).If playeritakes mixed strategies

then the expected values are

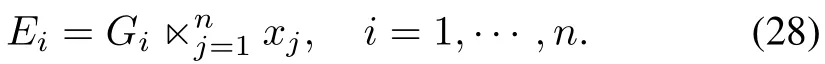
In Example 1,the composition of strategy dynamics of all players into pro file dynamics has been discussed.In the following,we consider the case of mixed strategy.

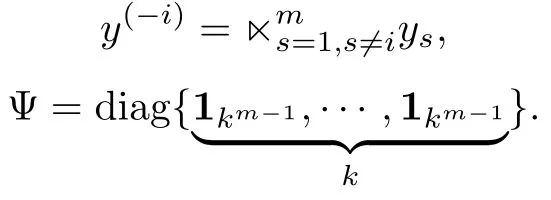
Lemma 2.Givenyi∈Υk,i=1,···,m,

Then we have the following decomposition formula:

Proof.First,note that ifX∈ΥpandY∈Υq,then∈Υpq.Denoteand set

Then it is clear that

It follows that

□

Remark 2.Assumeyi,xj∈∆k,i=1,···,m,j=1,···,n.Let

whereThen

whereand

For the probabilistic case,whereyi,xj∈Υk,the structure matrix can be calculated by(23).

To calculate the Nash equilibrium(s),we need the following lemma.It can be veri fied by a straightforward computation.

Lemma 3.AssumeX∈ΥpandY∈Υq.We define two dummy matrices,named“front-maintaining operator(FMO)”and“rear-maintaining operator(RMO)”respectively as

Then we have

Next,we expressxiby its independent components as

Then we have

whereand

Usingwe construct a matrix as

Then we have the following result.

Theorem 4.xi∈Υpi,i=1,···,nis a mixed strategy Nash equilibrium,if and only if they satisfy

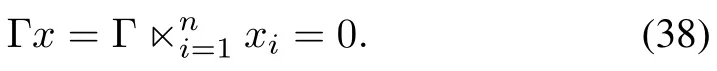
Proof.Necessity is obvious.As for the sufficiency,sinceis independent ofxsi,s=1,···,pi−1,then

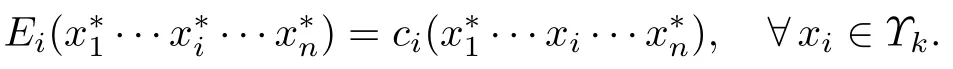
The conclusion follows.□

B.Numerical Algorithm

In this section,we explore a numerical algorithm for calculating Nash equilibrium.We define some sets:

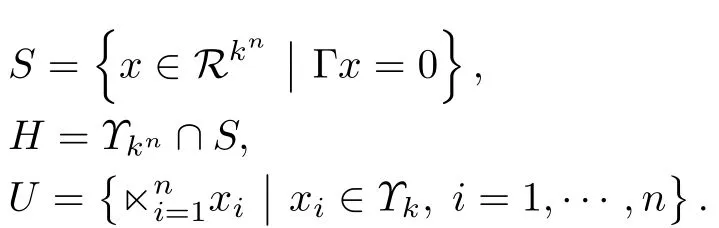
The following proposition comes from the definition.

Proposition 4.x∈Υpis a Nash equilibrium,if and only if

According to this proposition,we define two mappings:

1)ϕ:U→Has

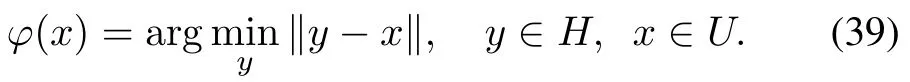
2)π:H→Uas

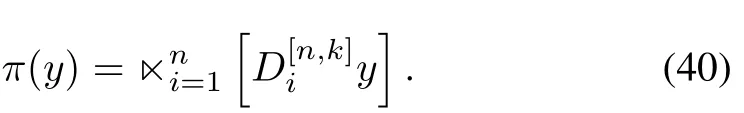
To seeϕis well defined,we consider the following problem:for a givenx0∈Rn,minimize(y−x0)T(y−x0),i.e.,

where

This is a quadratic programming problem;by checking the Karush-Kuhn-Tucker(KKT)condition,the solution is unique.That is,ϕis well defined[24].

Now we are ready to present the following algorithm,as shown in Fig.2.

Fig.2.Searching algorithm.

Algorithm 1.

Step 1.Choose a pointx0∈U.Findy0=ϕ(x0)∈H,and then findx1=π(y0)∈U.

Stepk.Findyk−1=ϕ(xk−1)∈H,and then findxk=π(yk−1)∈U.

Last step.If

stop.

C.A Numerical Example

Example 4.Consider the game of rock-scissors-paper(RS-P).The payoff bi-matrix is shown in Table VI.

TABLE VI PAYOFF BI-MATRIX OF R-S-P

Now assume there is a network of three players and the network graph is a complete graph,i.e.,any two nodes are connected.It is easy to figure out the payoff matrix as shown in Table VII.

TABLE VII OVERALL PAYOFF BI-MATRIX

It follows that

Using formula(36),we set

Then it is easy to calculateRi,i=1,2,3,4,5,6,as

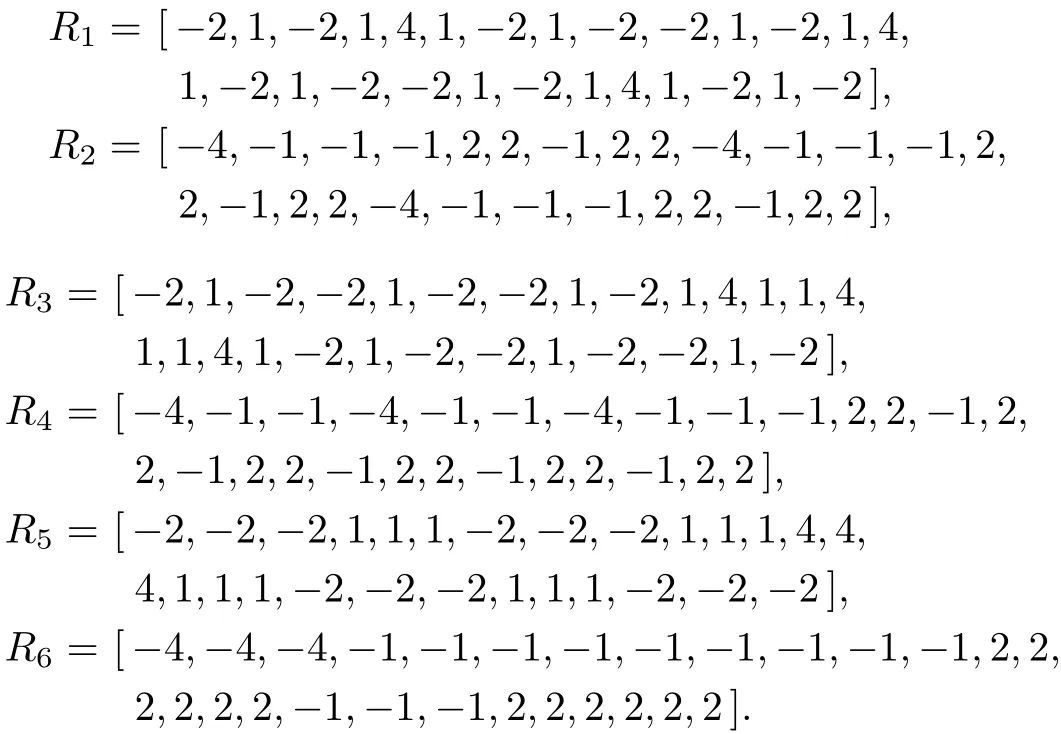
Finally,equation(38)becomes

It is easy to check that the strategy

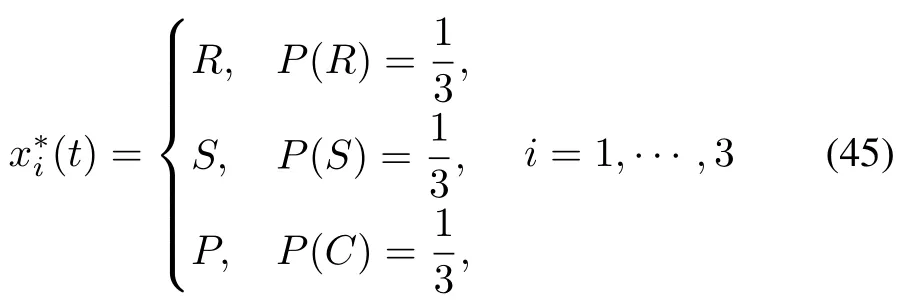
is a Nash equilibrium,because satisfies(44).

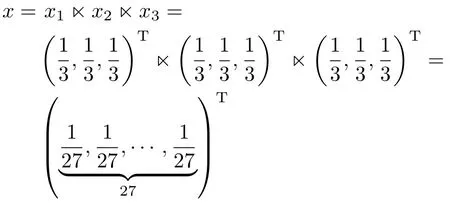
In fact,there are in finitely many Nash equilibriums.Algorithm 1 can be used to calculate some of them:Randomly choose an initial point as

then a Nash equilibrium is calculated as

Another initial point is chosen as

then the corresponding Nash equilibrium is

VI.NASH EQUILIBRIUM(S)OFNEGS

First,we consider the Nash equilibrium of a networked game(NG).

A.Static Case

Combining the results in the last two sections,it is clear that the algorithm developed in Section V can be used directly to find the static Nash equilibrium(s)based on the network pro file dynamics obtained in Section IV.But as the size of the network is not small,getting the overall network pro file dynamics is a heavy job.In this section,we consider how to get the global Nash equilibrium via the local one.

Let(N,E)be a graph.(N′,E′)is called a subgraph of(N,E)if 1)N′⊂N,E′⊂E;and 2)if(a,b)∈Eanda,b∈N′,then(a,b)∈E′.Let((N,E),G,Π)be an NEG.(N′,E′)is a subgraph of(N,E).Then((N′,E′),G,Π)is called a sub-NEG of((N,E),G,Π).

Note that subgraph(N′,E′)is uniquely determined byN′.So,we can simply sayN′is a subgraph of(N,E).If there is no possible confusion,we can also simply sayN′is a sub-NEG of((N,E),G,Π).

Now for eachUi,i∈N,we consider a sub networked static game.Using Theorem 4 and Algorithm 1,we can find the equilibrium:

Definition 7.The Nash equilibrium(46),obtained from the neighborhoodUi,is called a local Nash equilibrium of the NEG.

The following result is obvious.

Theorem 5.Assume there exists a set of local Nash equilibriums

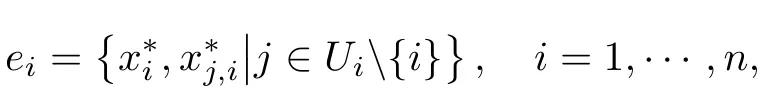
such that

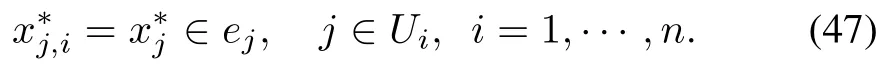
Thenis a global Nash equilibrium.

Example 5.Consider a cycle network described in Fig.3.Assume each player plays with its neighbors the game of rockscissors-paper as in Example 4.

Fig.3.A cycle network.

It is easy to check that the strategy

is both local and global Nash equilibrium.

B.Dynamic Case

In the dynamic case,that is,gameGis played repeatedly for in finite times(or forntimes),denoted byG∞(orGn),we first need payment criteria to verify the Nash equilibrium.The following criterion is adopted[25]:

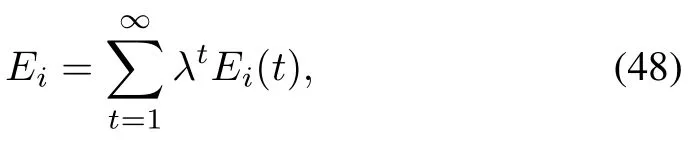
where 0＜λ＜1 is the discount factor.

An obvious fact is:if pro file=1,2,···}is a Nash equilibrium forG∞,then1≤t≤s}is also the Nash equilibrium for the finite time gameGt,1≤t≤s.Particularly,the initial pro fileis a Nash equilibrium forG1,which is considered as a static game.

Assume the SUR is fixed.Based on the above consideration,the following suf ficient condition is obvious.

Proposition 5.is a Nash equilibrium forG∞,if

1)is a Nash equilibrium for the static gameG1;

2)x(1)is a fixed point for the strategy dynamics

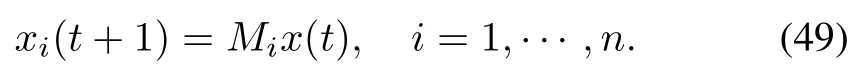
The following is a trivial example.

Example 6.Recall Example 4.It was shown there that

is a Nash equilibrium for the static game of rock-scissorspaper.To see whether it is also the Nash equilibrium,we have to check(49).Using Table VII and the technique demonstrated in Example 2,we can have the strategy dynamics of(49)with

Then it is ready to verify that

is a fixed point of(49).We conclude that

is the Nash equilibrium of the NEG.

VII.CONCLUSION

In this paper,we first give a detailed explanation for the structure of NEGs.The FEE is introduced and detailed algorithm for pro file dynamics is proposed.This part is based on our recent work[19],in which some related techniques have been developed.The main contribution of this paper is to investigate the Nash equilibrium(s)of NEGs.First,an algorithm is presented to calculate Nash equilibrium(s)of multi-player games.By analyzing the relationship between local and global Nash equilibriums,the above algorithm is applicable to find(one time)static Nash equilibrium(s)for NEGs.Finally,we present a sufficient condition to obtain dynamic Nash equilibrium(s)via static ones.What we did in this paper is a framework.Many problems remain for further investigation,and the technique proposed in this paper seems promising.

REFERENCES

[1]Axelrod R.The Evolution of Cooperation.New York:Basic Books,1984

[2]Smith J M,Price G R.The logic of animal con flict.Nature,1973,246(5427):15−18

[3]Holme P,Saram¨aki J.Temporal networks.PhysicsReports,2013,519(3):97−125

[4]Lv L,Medo M,Yeung C H,Zhang Y C,Zhang Z K,Zhou T.Recommender systems.Physics Reports,2012,519(1):1−49

[5]Bilbao J M.Cooperative Games on Combinatorial Structures.Boston:Kluwer Acadmic Publisher,2000

[6]Branzei R,Dimitrov D,Tijs S.Models in Cooperative Game Theory(2nd edition).Berlin:Springer-Verlag,2008

[7]Hauert C,Doebeli M.Spatial structure often inhibits the evolution of cooperation in the snowdrift game.Nature,2004,428:643−646

[8]Nowak M A,May R M.Evolutionary games and spatial chaos.Nature,1992,359(6398):826−829

[9]Santos F C,Santos M D,Pacheco J M.Social diversity promotes the emergence of cooperation in public goods games.Nature,2008,454(7201):213−216

[10]Rong Zhi-Hai,Tang Ming,Wang Xiao-Fan,Wu Zhi-Xi,Yan Gang,Zhou Tiao.Survey on complex networks.Journal of University of Electronic Science and Technology of China,2012,41(6):801−807(in Chinese)

[11]Wang Long,Fu Feng,Chen Xiao-Jie,Wang Jing,Li Zhuo-Zheng,Xie Guang-Ming,Chu Tian-Guang.Evolutionary games on complex networks.CAAI Transactions on Intelligent Systems,2007,2(2):1−10(in Chinese)

[12]Perc M.Evolution of cooperation on scale-free networks subject to error and attack.New Journal of Physics,2009,11:033027

[13]Szolnoki A,Perc M,Danku Z.Towards effective payoffs in the Prisoner′s Dilemma game on scale-free networks.Physica A,2008,387(8−9):2075−2082

[14]Wang Z,Szolnoki A,Perc M.Evolution of public cooperation on interdependent networks:the impact of biased utility functions.EPL,2012,97(4):48001

[15]Wang Z,Szolnoki A,Perc M.Interdependent network reciprocity in evolutionary games.Scientif i c Reports,2013,3:1183

[16]Perc M,Gardees J G,Szolnoki A,Floria L M,Moreno Y.Evolutionary dynamics of group interactions on structured populations:a review.Journal of Royal Society Interface,2013,10(80):20120997

[17]SzabG,Tke C.Evolutionary Prisoner′s Dilemma game on a square lattice.Physical Review E,1998,58(1):69

[18]Traulsen A,Nowak M A,Pacheco J M.Stochastic dynamics of invasion and fixation.Physical Review E,2006,74:011909

[19]Cheng DZ,He F,QiH S,Xu T.Modeling,analysis and control of networked evolutionary games.IEEE Transactions on Automatic Control[Online],available:http://lsc.amss.ac.cn/～dcheng/preprint/NTGAME02.pdf

[20]Cheng D Z,Qi H S,Li Z Q.Analysis and Control of Boolean Networks—A Semi-Tensor Product Approach.London:Springer,2011

[21]Cheng D Z,Qi H S,Zhao Y.An Introduction to Semi-Tensor Product of Matrices and Its Applications.Singapore:World Scientific,2012

[22]Gibbons R.A Primer in Game Theory.Glasgow:Bell and Bain Ltd.,1992

[23]Xie Zheng.An Introduction to Game Theory.Beijing:Science Press,2010(in Chinese)

[24]Bazaraa M S,Sherali H D,Shetty C M.Nonlinear Programming—Theory and Algorithms(3rd edition).Hoboken:John Wiley and Sons,2006

[25]Pal R,Datta A,Dougherty E R.Optimal in finite-horizon control for probabilistic Boolean networks.IEEE Transactions on Signal Processing,2006,54(6):2375−2387