一类月面钻进采样机构的鲁棒控制

郑燕红，邓湘金，姚 猛，赵志晖

(北京空间飞行器总体设计部，北京100094)

0 引言

从20世纪60年代以来，美国、苏联/俄罗斯、日本、欧空局先后开展了月球、火星、小行星、彗星等地外天体样品的采集、就位分析或样品返回.月球样品获取成就尤为显著，通过Apollo任务6次载人登月，苏联Luna任务3次无人采样返回，共获得了约382 kg月球样品.中国探月工程确定了绕、落、回三步走的发展思路［1］，随着嫦娥三号探测器在月面成功实现软着陆与巡视勘察，从月球上自动采集样品并返回地球将是后续中国深空探测的一项重要工作.

月面钻进采样是实现无人采样任务的重要手段，采样设备主要由采样控制器与采样机构配合完成土壤样品的采集.目前仅有苏联Luna 16/20/24完成了月球无人采样任务，文献［2］对采样机构形式、相关指标以及采样任务实施情况进行了介绍.其中Luna 16、Luna 20两次任务均发生了采样机构钻具卡滞现象.尤其是Luna 20在25 cm的钻进过程中由于卡滞导致过热，多次发生停转.Luna 24改进了采样机构设计，采样控制器针对月壤密实度可能的变化进行了输出功率适应性设计.Apollo 15采用了月球表面螺旋钻，获取月球次表层样品，当钻进深度大于0.9 m时，月壤密实度显著增加.Apollo 16、17在Apollo 15任务后针对钻杆接头与岩芯提取器进行了改进［3］，由于有宇航员的支持，可通过人为调整钻进速度，完成采样任务.从Luna、Apollo等任务实施过程来看，月面环境(尤其是月壤、温度等)的复杂性对采样过程有重要影响，但目前研制的钻进采样机构［4］主要集中在提升机构本身的能力方面，通过优化采样控制器控制律提高采样设备的适应性研究还较少.本文针对月面自动钻进采样机构，建立了进尺机构、回转机构名义控制模型，并分析了模型摄动、系统扰动下的控制系统模型，利用线性矩阵不等式方法进行了状态反馈鲁棒控制律设计，并针对有界模型摄动、系统扰动情况下状态反馈鲁棒控制系统的稳定性、干扰抑制情况进行了仿真分析.

1 采样机构控制模型

1.1 名义模型

中国月球探测可考虑回转与进尺复合运动钻进采样方式，完成月球次表层样品的采集.月面自动钻进采样设备工作过程中，钻杆与月壤相互作用，当进尺速度过快，回转速度偏小时，无法进入钻杆内部的月壤将会发生堆积，聚集应力将逐步增加，最终引起月壤卡滞钻杆;回转速度偏大，进尺速度过慢，钻杆处于慢进给转动状态，可能导致钻杆内部月壤出现较严重的混叠和散落，因此进尺速度与回转速度需满足一定的关系才能将无法进入钻杆内部的月壤以适当的速度通过外部螺旋排出，并使钻杆内部的月壤具有较好的层序状态.可见，回转与进尺复合钻进过程中，机构运动具有一定的耦合性，因此应对回转机构、进尺机构的控制系统进行联合设计.假设月面自动钻进采样设备回转机构、进尺机构分别采用直流电机驱动，则钻进采样时控制系统名义框图如图1所示.

图1中Lr、Lh分别为回转电机、进尺电机绕组电感;Rr、Rh为绕组电阻;ktr、kth为电机力矩常数;ker、keh为电机反电势常数;nr、nh为电机转速;Jr、Jh为电机等效惯量;k0为回转电机减速比，k1为进尺输出与回转输入电压比例系数.设进尺电机参考输入电压为uref，进尺电机阻力矩为Thf，回转电机阻力矩为Trf，进尺电机输出转速x1、绕组电流x2，回转电机输出转速x3、绕组电流x4为状态变量，并以进尺、回转电机输出转速为调节输出z1、z2，则对图1所示控制框图的状态方程为

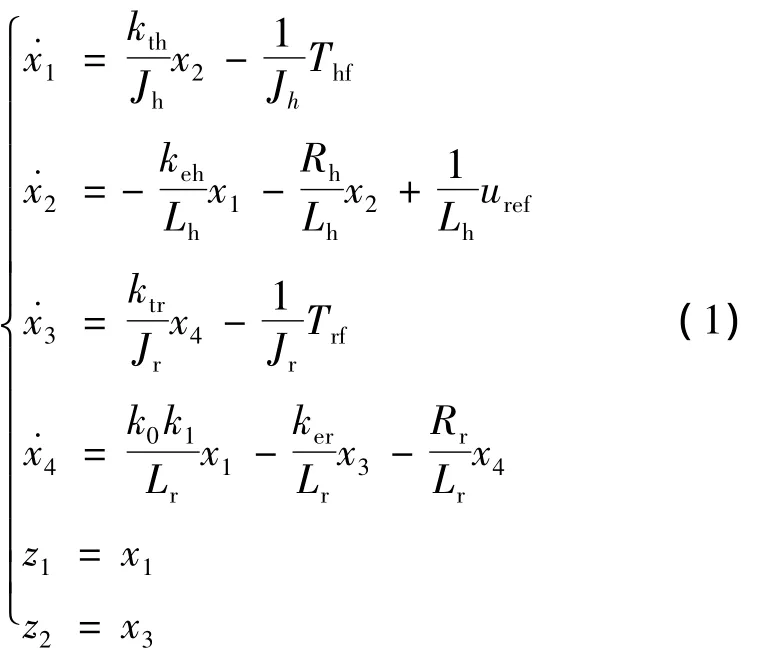
图1 钻进采样控制对象框图Fig.1 Diagram of a drill sampling control plant

1.2 摄动及扰动模型

月面与地面大气、温度环境存在较大差异，月昼期间月面温度往往高于地面环境温度，月面自动钻进采样设备的回转电机、进尺电机工作时，无法依靠大气对流散热，其温升特性将会发生一定的变化，电机的电阻、电感等内部参数会发生一定的漂移;从而导致模型具有参数不确定性，地面验证过程中具有良好性能设计的控制律在月面采样过程中性能可能下降，甚至不能工作.

另一方面，月球环境复杂，不同采样点、不同采样深度下，月壤状态存在较大的不确定性.月面钻进采样设备工作过程中需与月壤相互作用，月壤负载特性受颗粒大小、月壤密实度、钻进速度等多个因素影响，导致钻进过程中钻进的负载力矩发生波动.此外，钻进采样设备依靠多个轴承、齿轮以及减速器进行传动，月昼期间真空高温环境影响下，钻进采样设备各活动部件的润滑性能将发生一定的变化，机构内部阻力矩也会发生波动.月壤状态的不确定性、钻进采样设备传动特性的变化将为月面钻进过程带来扰动.

设月面钻进采样设备工作过程中，ω∈Rl为扰动量(如式1中［Thf，Trf］T)，u∈Rr为控制输入(如式(1)中uref)，且 ω、u在L2(0，∞)上有界，x∈ Rn为状态量(如式(1)中［x1x2x3x4］T)，z∈ Rm为调节输出(如式1中［z1z2］T)，则扰动影响下的状态空间模型，可描述为

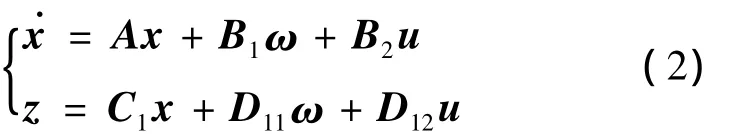
状态空间模型由系数矩阵完全确定，因此模型摄动可通过各系数矩阵的摄动表征，记式(1)描述的名义模型系数矩阵为 A0、B10、B20、C10、D110、D120，月面环境引起的参数摄动项记为EsubΔsubFsub，其中下标 sub 表示 a，b1，b2，c1，d11，d12，则 A=A0+EaΔaFa，B1=B10+Eb1Δb1Fb1，B2=B20+Eb2Δb2Fb2，C1=C10+Ec1Δc1Fc1，D11=D110+Ed11Δd11Fd11，D12=D120+Ed12Δd12Fd12.

其 中， Ea、Fa、Eb2、Eb1、Ec1、Ed11、Ed12、Fb1、Fb2、Fc1、Fd11、Fd12为加权阵，具有不确定结构.

2 鲁棒控制律设计

根据前面的分析，采样设备工作过程中存在模型摄动，并受到扰动影响，控制律设计需在摄动下保持系统稳定，在扰动下调节使输出量受到的影响尽可能小.从图1可见，状态变量为回转电机和进尺电机的电流、转速，可通过相应的传感器进行检测，因此，系统的状态变量可观测，可采用状态反馈设计.

将式(3)代入式(2)，引入p，q为中间变量并整理，可得

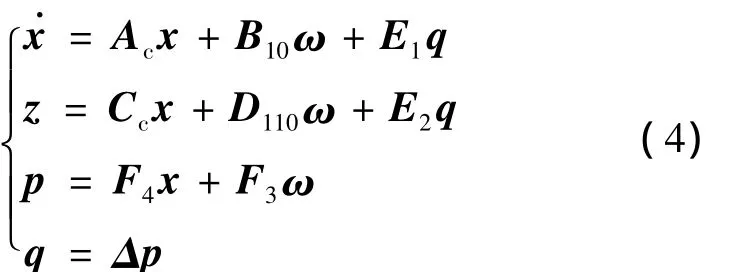
式中:Ac=A0+B20K;Cc=C10+D120K;E1=［EaEb2Eb10n×m0n×m0n×m］;E2=［0m×n0m×n0m×nEc1Ed12Ed11］;F3T=［0l×n0l×n

定理1.对给定的γ＞0，若存在矩阵W∈Rr×n，正定阵Q∈Rn×n，满足如下不等式:

从认知论角度分析，知识一般分为显性知识和隐性知识两大类。显性知识是指通过语言或其它方式描述、记录的系统化知识，是方便学习、流通、共享的外在化知识；隐性知识是高度个人化的知识，它依赖于个人的经验或感悟，存在于人的大脑中，只能通过直接的、面对面地接触才能实现交流和共享。显性知识和隐性知识是可以实现相互转化和相互促进的。

则对式(4)描述系统内稳定，且扰动量ω到调节量z的闭环传递函数的H∞范数，其中状态反馈阵K=WQ-1，*表示矩阵沿主对角线对称元素的转置，其中I为单位矩阵.

证明.记 P=Q-1，K=WQ-1，以 diag{Q-1，I，I}对N0作合同变换，得

由 Schur补引理［5］N＜0，等价于

记r1=xTωTqT，则对式(6)，有

设V(x)=xTPx，式(7)转化为

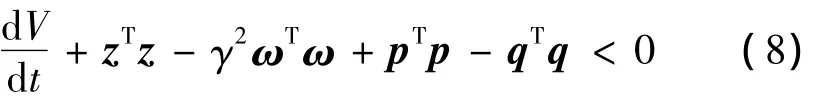
由式(8)两边对时间t从0到∞积分，并考虑，且系统为零初始状态V(0)=0，有

考虑式(4)系统的内稳定性［6-7］问题，z为调节输出对稳定性无影响，在零输入条件下系统模型为

由N0＜0，引入矩阵，对N0作合同变换，则有STN0S＜0，即

从而有

由有界实引理［8］可知，式(13)成立，则有q到 p的闭环传递函数的H∞范数，式(10)线性分式描述如图2所示.

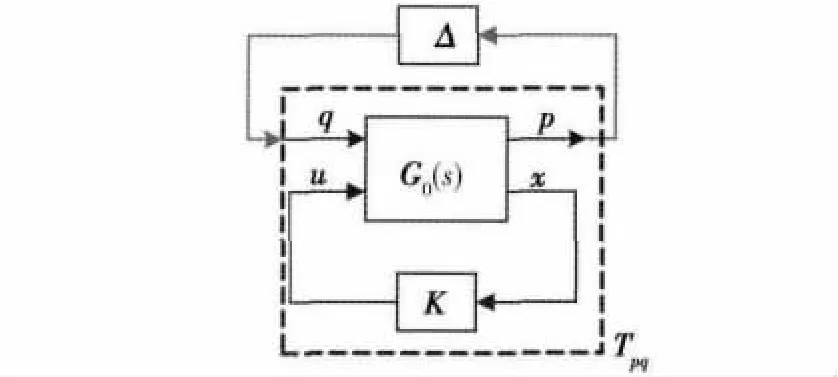
图2 无外部输入下的线性分式框图Fig.2 Diagram of linear fraction transform without outer input

其中:

根据小增益定理［9］，系统内稳定需＜1，由于，因此系统内稳定.

因此，对模型摄动与扰动影响下的采样设备模型式(2)的状态反馈鲁棒控制律设计可转化为:对给定的γ＞0，寻找满足定理1的W、Q，使γ，其中状态反馈阵K=WQ-1.

3 仿真分析

为验证控制律设计的有效性，设钻进采样设备的回转电机、进尺电机具有如下的名义参数值，ker=0.15 V/(r/min)，ktr=0.32 N·m/A，Lr=0.000 7 H，Rr=0.7Ω，Jr=1.7 × 10-4kg·m2，Lh=0.000 3 H，keh=0.01 V/(r/min)，kth=0.1 N·m/A，Rh=0.3 Ω，Jh=2.4 ×10-4kg·m2，进尺电机减速比为k0=1∶6，进尺输出转速与回转输入电压比例系数k1=0.75 V/(r/min)，则由式(1)可知，钻进采样设备名义状态空间模型系数矩阵为

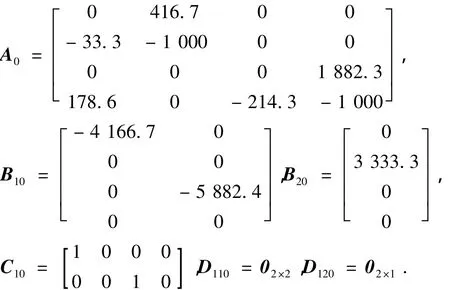
考虑在月面工作过程中，回转电机、进尺电机各参数摄动为名义值的5%，由于此处选定的调节输出为回转电机、进尺电机直接输出的转速，其系数矩阵无摄动，因此，可确定名义模型各系数矩阵的摄动系数阵为

利用Matlab求解可得

从状态反馈阵K各参数值可知，当以进尺电机参考电压输入时，进尺电机输出转速、绕组电流通过负反馈确保输出转速在负载下的平稳性，而回转电机输出转速、绕组电流通过正反馈调节控制量，确保回转转速在负载下的平稳性.当回转转速偏高时，其排出土壤的能力增强，可提高进尺电机电压，加快钻进速度;当回转转速偏低时，其排出土壤的能力减弱，若此时进尺电机电压维持或增大，钻进过程中多余的土壤无法及时排出，导致钻杆发生卡滞现象，因此回转转速偏低时，进尺电机参考电压也应降低.

考虑回转电机、进尺电机参数摄动时 Δa=fI4×4，Δb2=fI4×4，f=±0.3、±0.6、±0.9，I4×4为单位阵.此时，控制系统的阶跃输出响应曲线如图3所示，可见回转电机、进尺电机控制系统在不同的模型摄动下均可在约0.12 s内快速到达稳态，摄动影响下进尺电机转速稳态值为49.43～51.20 rad/s，考虑6∶1的减速比，月面钻进采样设备进尺机构输出转速为 8.24 ～8.53 rad/s，相对名义模型下 8.38 rad/s转速的最大波动约为1.79%;摄动影响下回转电机转速稳态值为 39.58 ～44.82 rad/s，考虑 2∶1 减速比，回转机构输出转速为 19.79 ～22.41 rad/s，相对名义模型下20.94 rad/s转速的最大波动约为7%.可见，采样控制器在采用状态反馈鲁棒控制律的情况下，回转电机、进尺电机参数名义值摄动不大于5%，回转电机转速输出波动不大于7%，进尺电机转速输出波动不大于1.875%，系统可保持稳定，并能快速到达稳态.

图3 模型摄动状态下的响应曲线Fig.3 Response for a model with perturbation

考虑施加幅度不大于0.5 N·m的随机噪声ω1，幅度不大于2.5 N·m的随机噪声ω2，同时考虑模型摄动 Δa=0.5I4×4，Δb1=0.5I4×4，Δb2=0.5I4×4，利用上述状态反馈阵K，可得摄动与干扰并存情况下，对进尺电机、回转电机输出转速的影响.从图4～5可见进尺电机转速最大将下降约2.62 rad/s，相对名义模型无扰动情况，下降约5.2%;回转电机转速最大将下降5.24 rad/s，相对名义模型无扰动情况，下降约12.5%.可见，采样控制器在采用状态反馈鲁棒控制律的情况下，当回转电机、进尺电机参数摄动不大于2.5%、进尺电机干扰力矩不大于0.5 N·m、回转电机干扰力矩不大于2.5 N·m时，回转电机转速输出波动不大于12.5%，进尺电机转速输出波动不大于5.2%，系统保持稳定.

图4 干扰力矩作用下进尺电机输出转速曲线Fig.4 Rotary velocity curves of the pull motor with disturbance torque

图5 干扰力矩作用下的回转电机输出转速曲线Fig.5 Rotary velocity curves of the rotation motor with disturbance torque

4 结论

本文针对月面自动钻进采样设备复合钻进过程，建立了模型摄动与系统扰动下的采样机构控制模型，利用线性矩阵不等式方法推导了钻进采样设备状态反馈鲁棒控制律，仿真分析表明该控制律在L2(0，∞)有界摄动、随机噪声扰动存在的情况下仍可保持系统稳定，当采样机构电机参数摄动不大于5%时，回转转速波动不大于7%，进尺转速波动不大于1.875%;当进尺干扰力矩不大于0.5 N·m、回转干扰力矩不大于2.5 N·m时，回转电机转速输出波动不大于12.5%，进尺电机转速输出波动不大于5.2%.

［1］叶培建，彭兢.深空探测与中国深空探测展望［J］.中国工程科学，2006，8(10):13-18.YE P J，PENG J.Deep space exploration and its prospect in China［J］.Engineering Science，2006，8(10):13-18.

［2］刘志全，庞彧，李新立.深空探测自动采样机构的特点及应用［J］.航天器工程，2011，20(3):120-125.LIU Z Q，PANG Y，LI X L.Characteristics and applications of automatic sampling mechanisms for deep space exploration［J］.Spacecraft Engineering，2011，20(3):120-125.

［3］NASA.Apollo program summary report synopsis of the Apollo program activities and technology for lunar exploration［R］.Houston:Lyndon B.Johnson Space Center，1975.

［4］YOSEPH B C，KRIS Z.Drilling in extreme environments-penetration and sampling on Earth and other planets［M］.Weinheim:Wiley-VCH Verlag GmbH ＆ Co.KGaA.2009:48-51.

［5］王广雄，王新生，何朕.H∞控制器的 LMI算法分析［J］.电机与控制学报，2002，6(1):46-49.WANG G X，WANG X S，HE L.On algorithms of LMI-based H∞controller［J］.Electric Machines and Control，2002，6(1):46-49.

［6］SIGURD S，IAN P.多变量反馈控制——分析与设计［M］.韩崇昭，译.西安:西安交通大学出版社，2011:45-52.

［7］俞立.鲁棒控制——线性矩阵不等式处理方法［M］.北京:清华大学出版社，2002:8-9.

［8］ZHOU K M，DOYLE J C，GLOVER K.鲁棒与最优控制［M］.毛剑琴，译.北京:国防工业出版社，2002:250-252.