卫星姿态控制系统的故障可诊断性评价研究*

李文博，王大轶，刘成瑞

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

0 引言

对于动态控制系统，故障可诊断性包括可检测性和可隔离性.其中，故障可检测性是指［1］:在系统存在干扰的情况下，利用输入和输出信息在有限时间间隔内检测出故障的发生.从其定义中可以看出:故障可诊断性是系统的内在本质属性，反映了系统对于故障能否被诊断的能力.为提高控制系统的故障诊断能力，现有文献和主要研究成果多集中于诊断算法，而忽视了系统的内在可诊断性.

随着控制系统规模和复杂性的增加，为实现全状态监测，要求配置更多数量的传感器.然而，由于质量、体积和安装等客观因素的限制，不可能无限制增加传感器的个数，这使得有限数量的传感器难以反映所有变量的变化情况，从而导致在实际型号中卫星姿态控制系统的故障可诊断性较低;同时，只有保证系统的故障可诊断性得到满足，设计诊断算法才具有意义.可诊断性评价作为控制系统可诊断性研究中的关键问题，能够在系统设计阶段明确故障能否被诊断，从而为诊断算法的设计提供依据，并通过传感器的优化配置实现在设计阶段提高系统故障诊断能力的工程目标［2］.因此，对于卫星姿态控制系统进行故障可诊断性评价研究具有重要的实际工程意义.

文献［3-5］通过多项式基、等价空间、互质分解等方法设计残差，并根据残差的存在性进行可诊断性评价.但是，上述作法所得评价结果严重依赖于残差/诊断算法的设计精度，并不能准确反映可诊断性能.

对于工程人员来说，不依赖于任何诊断算法进行可诊断性评价更具有实际意义.在此前提约束下，文献［6］利用故障到输出之间传递函数的存在性，进行可诊断性分析;文献［7］通过系统的输入/输出关系构造关联矩阵，并根据故障在关联矩阵中的具体形式表征可诊断性;文献［8］和［9］将故障视作一种扩展状态，并根据新扩展系统的可观测性评价传感器故障和执行器故障的可诊断性.文献［10］通过数学仿真比较了存在反馈控制和开环控制时系统的可诊断性;通过大量的研究发现［11-12］:现有基于模型的可诊断性评价研究多针对开环系统，但对闭环系统尚有许多不适之处.文献［13］借鉴文献［8］中开环系统可诊断性评价研究的思想，对闭环系统传感器和执行器的加性故障进行可诊断性评价，但没有考虑模型不确定性和乘性故障.

针对上述研究中存在的不足，在文献［13］的基础上，本文以卫星姿态控制系统为研究对象，并考虑其模型不确定性，依次分析传感器和执行器加性故障和乘性故障的可诊断性.

1 卫星姿态控制系统的数学模型

卫星姿态控制系统的动力学方程为［14］

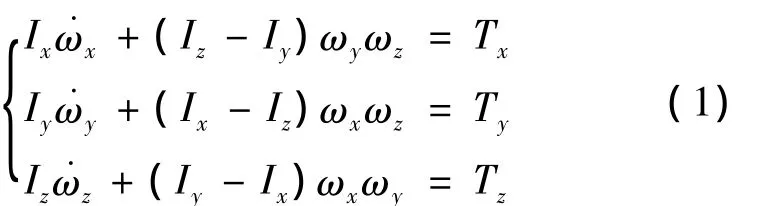
式中:Ii(i=x，y，z)为卫星在3个惯性主轴的转动惯量;ωi为卫星姿态角速度矢量ω在主惯量轴上的投影;Ti为控制力矩沿主惯量轴的分量.

当卫星相对轨道坐标系的姿态角(包括:滚动角φ、俯仰角θ和偏航角ψ)均为小量时，运动学方程为［15］

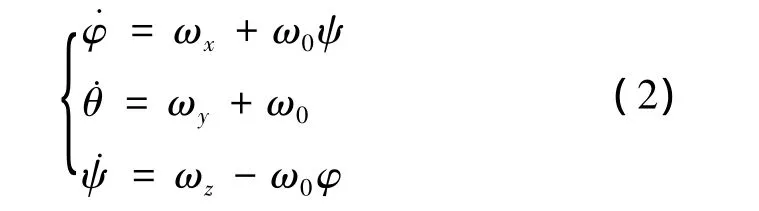
式中ω0为卫星的轨道角速度.

式中:Af=A0+ΔA为包含建模不确定性的系统矩阵，(ΔA表示模型不确定性);w(k)和v(k)分别为系统过程和观测噪声，可描述成线性互不相关的高斯白噪声.相关矩阵的具体形式为

常用的PID控制器模型为

式中，xc(k)=x(k)表示控制器的状态变量，r(k)表示期望值，相关矩阵的具体形式为

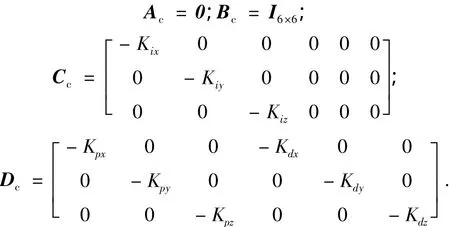
分别令 X=［x xc］T和 Y=［y u］T，将式(3)和(4)合并，得到姿态控制系统的闭环状态空间模型:

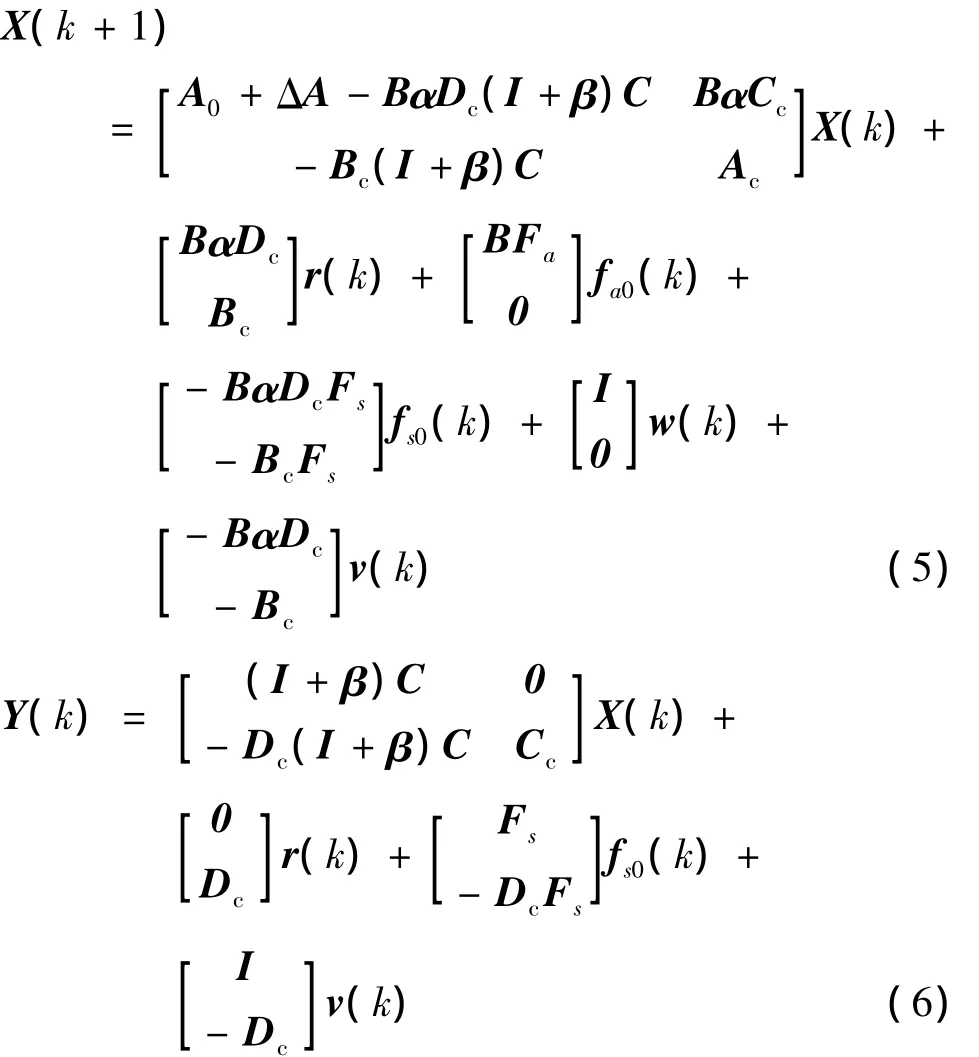
2 加性故障的可诊断性评价

式(5)和(6)不仅描述卫星姿态闭环控制系统的内在属性，还考虑了建模不确定性ΔA、过程噪声w和干扰噪声v的影响.在进行系统固有可诊断性评价时，将忽略上述过程和干扰噪声的影响，并将执行器和传感器故障(包括:乘性和加性故障)作为状态变量对原系统进行扩维，即将故障的可诊断问题转换成增广系统的状态可观性问题.

在此先给出如下引理:

引理1［16］.令S(A)表示矩阵A中所有特征值的集合，则(A，C)具有可观测性的充要条件为:若Aχ=λχ且Cχ=0，则表明每个特征值λ∈S(A)所对应的特征向量都有χ=0.

引理2［17］.令S(A)表示矩阵A中所有特征值的集合，则(A，C)具有可观测性的充要条件为

式中n表示系统的维数.

考虑到加性故障的一般特点是:动态性能已知而发生时间和初始状态未知，分别按式(7)和(8)构造执行器和传感器的加性故障模型

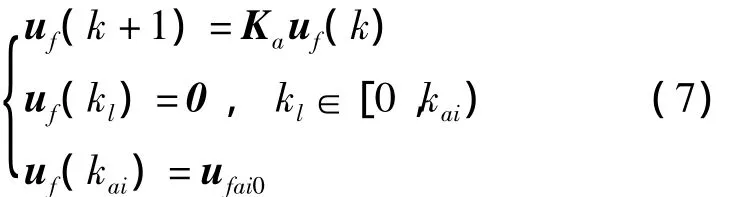
式中:Ka表示执行器故障的特性，用于描述具体故障模式;kai和ufai0分别为第i个执行器故障的发生时刻和初始状态，一般未知

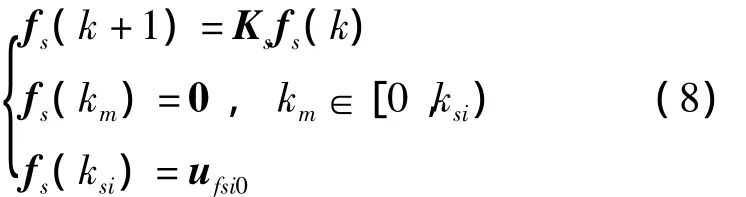
式中:Ks表示传感器故障的特性，用于描述具体的故障模式;ksi和ufsi0分别为第i个传感器故障的发生时刻和初始状态，一般未知.

2.1 模型精确时加性故障的可诊断性评价

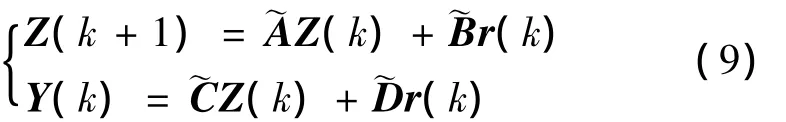
式中:

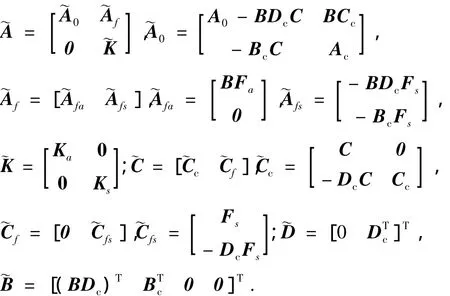
在此通过定理1，给出模型精确时卫星姿态闭环控制系统加性故障进行可诊断性评价的前提条件.

定理1．对于式(9)所示闭环系统模型，当模型精确时其加性故障具有可诊断性的充分条件为:

2)描述故障动态特性和其在观测变量中分布情况的状态空间模型(，ACf)具有可观测性;

3)描述姿态动力学和运动学、控制器、故障动态特性及其在观测变量中分布耦合关系的状态空间模型具有可观测性．

证明．

具体针对以下3种工况进行详细阐述．

此时，λ=且 λ=．当假设完全可观测时，可得:χ1=0．式(10)改写为

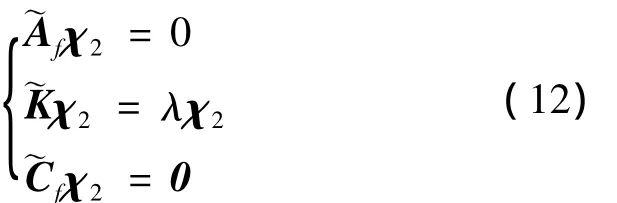
此工况，λ=且 λ ≠，即．因此，可得:

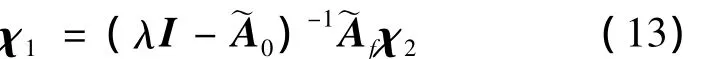
将式(13)代入式(10)中，可得

HClO和HNO3一样具有很强的氧化性,都属于强氧化性酸,为此好多同学就容易误认为ClO-和NO-3一样,只有在酸性的溶液中才能体现出它的强氧化性。事实上ClO-在碱性的溶液中就可以表现出氧化性,这一点和NO-3是不同的,ClO-作为一种弱酸的酸根,在水溶液中水解呈现碱性,也就是说它本身存在的环境就是碱性,ClO-在碱性条件下就可以把一些还原性离子给氧化,典型的反应有:

针对以下两种工况进行详细阐述．

同理于上述工况1．

同理于上述工况3．

2．2 存在模型不确定时加性故障的可诊断性评价

同理，本小节通过定理2给出存在模型不确定性时卫星姿态闭环控制系统加性故障进行可诊断性评价的前提条件．

定理2．当存在建模不确定性时，式(9)所示闭环系统模型中加性故障具有可诊断性的充分条件为:

1)当建模不确定性ΔA、执行器和传感器加性故障的分布矩阵Fa和Fs对系统动力学模型(A0，C)的可观性不产生影响，即满足:

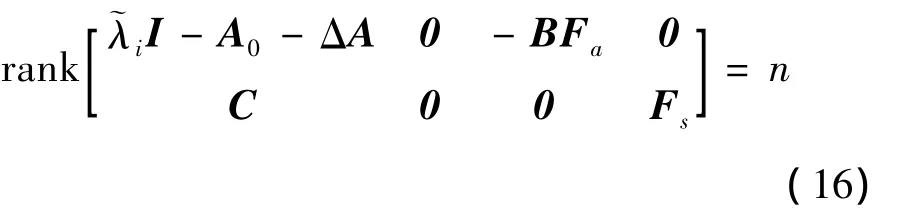
2)控制器状态空间模型(Ac，Cc)具有可观测性;

3)执行器和传感器故障动态特性Ka和Ks与系统动力学和控制器系统矩阵A0和Ac具有不同的特征值;

4)实现执行器和传感器的加性故障隔离，需保证执行器故障动态特性Ka的集合S(Ka)和传感器故障动态特性Ks的集合S(Ks)没有交集，即S(Ka)∩S(Ks)=Ø．

证明．

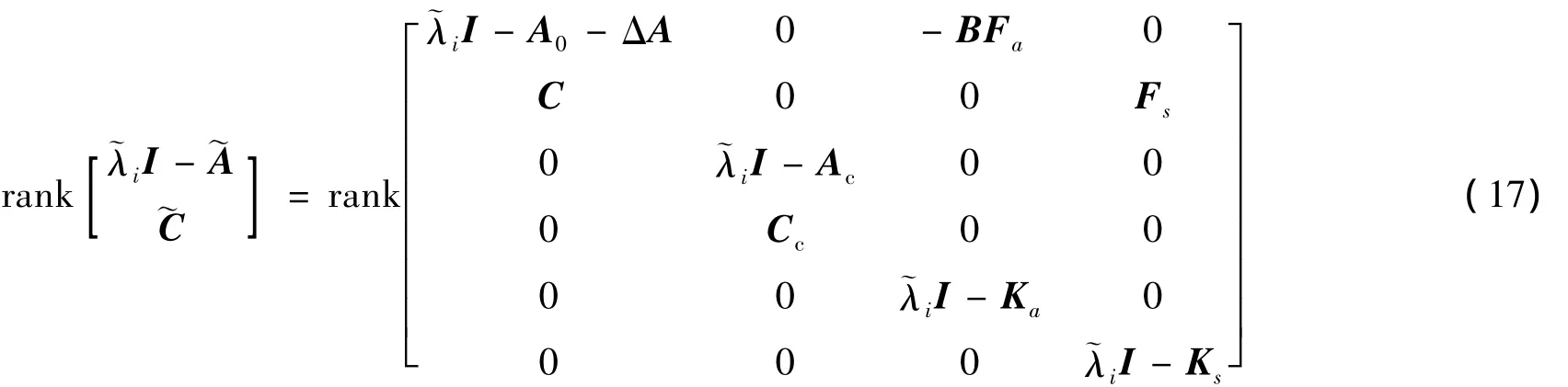
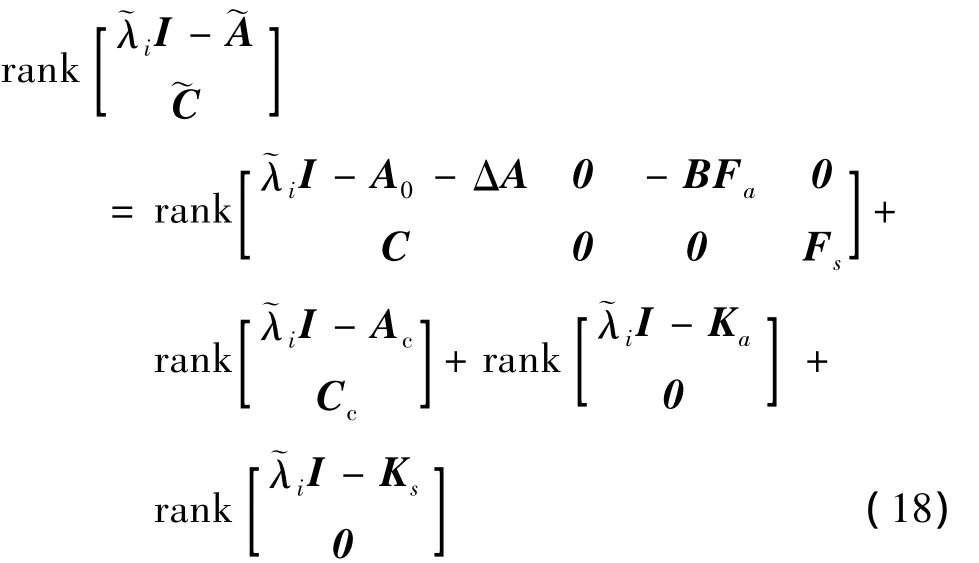
只要保证上述4部分中每一个状态空间模型的PBH判别矩阵满秩，即保证系统的状态变量具有可观测性.

此时，定理2得证.

根据定理2可以引申出如下结论:

1)当执行器故障特性 Ka、传感器故障特性Ks、动力学模型系统矩阵A0和控制器系统模型Ac具有不同的特征值时，卫星姿态闭环控制系统的加性故障具有可检测性和可分离性;

2)当Ka、Ks、A0和Ac具有相同的特征值时，若和满足 可观测性条件，则闭环系统的加性故障具有可诊断性.

3 乘性故障的可诊断性评价

当执行器和传感器的故障形式为乘性故障时，即fa0=0、fs0=0和ΔA≠0，将其代入到式(5)和(6)中，可得

式中:

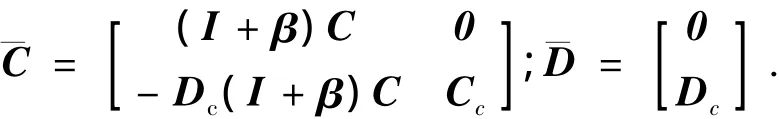
从式(19)中可以看出:不同于加性故障，乘性故障直接通过状态变量表现其特性.因此，只要系统状态变量是可观测的，就能保证故障具有可诊断性.定理3.对于式(19)所示系统中乘性故障具有可诊断性的充分条件是:

1)卫星姿态动力学和运动学的状态空间模型(A0，C)具有可观测性;

2)控制器状态空间模型(Ac，Cc)具有可观测性;

3)模型不确定性ΔA和传感器乘性故障β对状态空间模型(A0，C)的可观测性没有影响.证明.

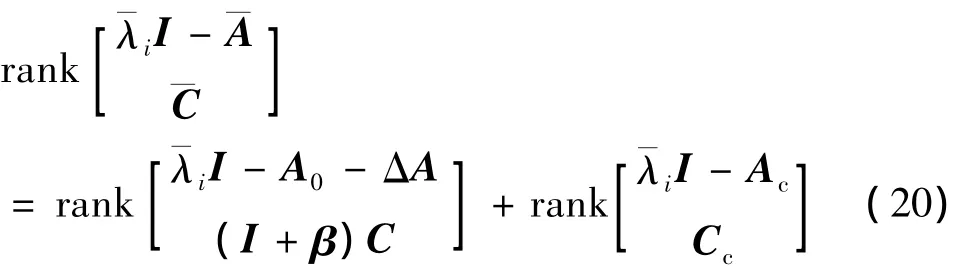
根据式(20)可得:当 (A0，C)和 (Ac，Cc)均可观测时，若要使得系统对于乘性故障具有可诊断性，需保证:

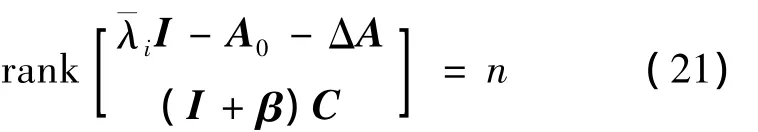
即传感器乘性故障β和模型不确定性ΔA 对动力学模型的秩不影响.

综上所述，得到定理3所述卫星姿态闭环控制系统乘性故障具有可诊断性的判别条件.

在此需要说明的是，本文所提基于状态可观的故障可诊断性评价方法隐含如下条件［18］:Ka和Ks均为常数，即本方法只对满足这一要求的故障模式有效，而对其余故障模式无效.

4 结论

为实现在地面设计阶段提高卫星姿态控制系统故障诊断能力的工程目标，本文将故障视作扩展状态，通过新扩展系统的状态可观测性评价加性故障和乘性故障的可诊断性，并通过定理1、2和3给出可诊断性判别的充分条件，重点考虑闭环系统特性和模型不确定性对评价结果的影响.该方法简单可行、不依赖于任何诊断算法，所得结论能够为控制系统设计提供参考依据.

［1］GOBBO D D，NAPOLITANO M R.Issues in fault detectability for dynamic systems［C］//The 26thAmerican Control Conference.Chicago:AACC，2000:28-30.

［2］刘文静，刘成瑞，王南华.故障可诊断性评价与设计研究进展［J］.航天控制，2011，29(4):72-78.LIU W J，LIU C R，WANG N H.Overview of fault diagnosability evaluation and design［J］.Aerospace Control，2011，29(4):72-78.

［3］NYBERG M，NIELSEN L.Parity functions as universal residual generators and tool for fault detectability analysis［C］//IEEE Conference on Decision and Control.San Diego:IEEE，1997:4483-4489.

［4］CHOW E Y，WILLSKY A D.Analytical redundancy and the design of robust failure detection systems［J］.IEEE Transactions On Automatic Control，1984，29(7):603-614.

［5］FRISK E，NYBERG M.A minimal polynomial basis solution to residual generation for fault diagnosis in linear systems［J］.Automatica，2001，37(9):1417-1424.

［6］DING S X.Model-based fault diagnosis techniques:design schemes，algorithms and tools［M］.London:Springer，2013:51-68.

［7］Travé M L，ESCOBER T，OLIVE X.Diagnosability analysis based on component-supported analytical redundancy relations ［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part A，2006，36(6):1146-1159.

［8］闻新，张洪钺，周露.控制系统的故障诊断和容错控制［M］.北京:机械工业出版社，1998:31-35

［9］周东华，孙优贤.控制系统的故障检测与诊断技术［M］.北京:清华大学出版社，1994:177-191

［10］姜苍华，周东华.基于观测器的线性系统故障检测方法性能比较研究［J］.计算技术与自动化，2003，22(2):58-62.JIANG C H，ZHOU D H.Performance comparison studies of observer based fault detection methods for linear systems［J］.Computing Technology and Automation，2003，22(2):58-62.

［11］ISERMANN R.Process fault detection based on modeling and estimation methods-a survey［J］.Automatica，1984，20:387-404.

［12］WHISKY A S.A survey of design methods for failure detection in dynamic systems［J］.Automatica，1976，12:601-611.

［13］邢琰，吴宏鑫.闭环控制系统故障可检测性研究［J］.中南大学学报(自然科学版)，2005，36:528-532.XING Y，WU H X.Fault detectability of closed-loop control systems［J］.J.Science and Technology，2005，36:528-532.

［14］章仁为.卫星轨道姿态动力学与控制［M］.北京:北京航空航天大学出版社，2005:147-184

［15］刘文静，王南华.面向资源约束航天器控制系统的故障检测研究［J］.宇航学报，2011，32(7):1527-1533.LIU W J，WANG N H.FD for spacecraft control systems with resource constraint［J］.Journal of Astronautics，2011，32(7):1527-1533.

［16］李娟，吕新丽.含两类时滞的线性系统的故障诊断及故障可诊断性［J］.计算机应用研究，2009，26(10):3727-3742.LI J，LV X L.Fault diagnosis and diagnosability for linear systems with two kinds of time-delays［J］.Application Research of Computers，2009，26(10):3727-3742.

［17］李娟，赵友刚，于洋，等.含大时滞和噪声的网络化控制系统的最优故障诊断［J］.自动化学报，2012，38(5):858-864.LI J，ZHAO Y G，YU Y，et al.Optimal fault diagnosis for networked control systems with large time-delays and noises［J］.Acta Automatica Sinica，2012，38(5):858-864.

［18］刘文静.航天器控制系统故障可诊断性及在轨故障诊断方法研究［D］.北京:北京控制工程研究所，2011.LIU W J.On the fault diagnosability and in-orbit fault diagnosis approach for spacecraft control system ［D］.Beijing:Beijing Institute of Control Engineering，2011.