基于粒子群算法的多脉冲转移轨迹优化*

陈 全，杨 震，罗亚中

(国防科技大学航天科学与工程学院，长沙410073)

0 引言

空间脉冲轨道机动问题是自20世纪50年代以来就得到广泛研究的航天器轨迹优化问题［1-3］.早期的研究主要基于开普勒轨道解析分析算法，通过函数极值条件确定脉冲转移轨道的最优性条件.此后随着研究问题的复杂程度增加，单一的解析分析方法难以奏效，间接法和直接法得到了发展.前者主要是基于主矢量理论构造优化模型，后者则是构造一般性非线性规划模型.在20世纪90年代之前主要采用梯度优化算法，此后遗传算法等进化算法得到了广泛应用.最近十多年，通过构造一般性优化模型，采用进化算法来完成脉冲轨道机动问题是广泛采用的研究思路［3-6］.

轨道机动问题通常包括3类问题:拦截、转移和交会［2］.目前对于多脉冲最优交会问题，有相对成熟的基于Lambert算法构造的一般性多脉冲最优交会优化模型，并得到了广泛应用［4-6］;而对多脉冲最优转移一般性优化模型的研究则较少，只有Abdelkhalik 和 Mortari［7］作了初步研究.

本文在文献［7］和［8］的研究基础上，对基于Lambert算法的多脉冲最优转移一般性优化模型进行了探讨.文献［7］中仅以脉冲变轨处航天器真近点角作为设计变量，本文同时探讨了脉冲时刻作为设计变量的优化模型，并对比分析了优化效果;此外本文采用粒子群优化(PSO，particle swarm optimization)算法［9］求解优化问题，该算法新近在航天器小推力轨道优化［10］、多脉冲交会轨道优化［11］等中得到了成功应用，本文通过仿真研究表明，其性能优于文献［7］中使用的遗传算法.

1 多脉冲转移轨迹优化问题描述

1.1 Lambert问题

Lambert问题是轨道动力学中的两点边值问题.在给定航天器初始位置r1、终端位置r2和转移时间Δt的情况下，通过求解转移时间方程获得航天器在r1、r2处的速度v1、v2.Lagrange形式的转移时间方程［12］可表示为

式中，μ为地球引力常数，α、β为Lagrange参数，a为转移轨道半长轴，s=(r1+r2+d)/2，N为转移圈数，d=|r1-r2|，r1，r2分别为位置矢量 r1，r2的模.本文采用Vallado［12］求解 Lambert问题的普适变量算法，转移速度公式为

若初始和终端时刻航天器速度分别为v-1，v+2，则Lambert转移所需要的总速度增量为

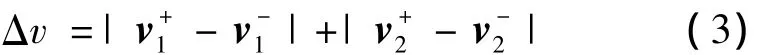
式中“-”、“+”分别表示变轨前和变轨后通过式(2)求解.

当式(1)中的转移时间Δt较短时，Lambert转移轨道仅有一条，此时Lambert转移轨道就是燃料最省轨道.当飞行时间较长时，Lambert转移轨道有2N+1条［12］，直接采用式(2)算法获得的转移轨道是其中一个解，该转移轨道呈现较大的偏心率，即航天器要沿这条轨道飞行很长的路程才能完成转移，这样的燃料消耗巨大，为实际工程所不允许，此时需要求解多圈Lambert问题，从其2N+1个解［12］中寻找最省时间或最省燃料解.

1.2 多脉冲轨道转移问题

工程应用中航天器轨道转移的脉冲数目一般大于2，多脉冲轨道转移示意如图1所示.二体假设下，航天器轨道动力学方程为

方程(4)的解可表示为 r(t+Δt)=p(r(t)，v(t)，t，t+Δt)和 v(t+Δt)=q(r(t)，v(t)，t，t+Δt).

图1 N脉冲转移轨道示意图Fig.1 N-impulse orbit transfer

脉冲假设下，航天器变轨前后状态可表示为

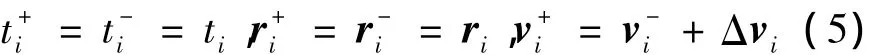
假设航天器在初始t0时刻状态为r0，v0，终端0+Δt时刻状态为 rf，vf，则该问题即寻找ti，Δvi，(i=1，2，…，n)在满足如下约束的条件下:

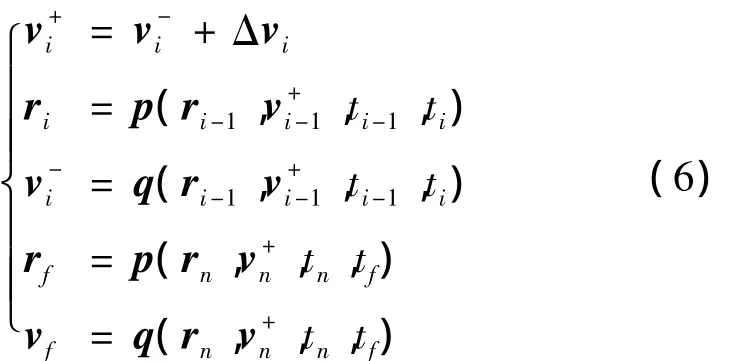
使得总速度增量最小

对转移时间较短的两脉冲变轨，式(6)存在唯一解，可通过求解Lambert问题获得最省燃料转移轨道;对转移时间较长的两脉冲变轨或n＞2的多脉冲变轨，式(6)的解不唯一，需要通过求解多圈Lambert问题或优化多脉冲变轨方案以寻找满足约束的最省燃料转移轨道.式(6)～(7)所示优化问题的参数化处理方法可以分为可行解迭代算法和非可行解迭代算法.前者迭代过程中无需约束处理，所产生的每一个解均为可行解;而后者则需要算法的最终收敛才能获得可行解［3，5］.试验表明，可行解迭代算法的收敛效率比非可行解好，但其优化变量需要进行精心设计.

1.3 基于Lambert算法的多脉冲转移轨迹优化模型

方程(6)所示的优化模型适用于一般的多脉冲共面或异面轨道转移问题.二体假设下，航天器所在的初始轨道可由5个轨道根数确定:半长轴aI，偏心率eI，轨道倾角iI，升交点赤经ΩI和近地点幅角ωI确定.同理，终端轨道由aF，eF，iF，ΩF和 ωF确定.本文考虑的轨道转移问题不限制航天器到达终端轨道的时间及位置，即终端真近点角θF、转移时间Δt为自由设计变量.

为了瞄准终端位置速度，至少需要施加2次机动.当机动脉冲数目n≥2时，设计变量一共4n个，包括脉冲施加时刻(n个)和脉冲分量(3n个).为了建立可行解迭代优化模型，本文首先选取最后2次脉冲(共6个脉冲分量)用于满足终端约束条件，通过求解Lambert问题获得;其余4n-6个设计变量通过粒子群优化算法给出.当不限制航天器到达终端轨道的时间及位置时，优化变量一共有4n-5.

对二体轨道，可分别采用时间或真近点角来表示航天器在轨位置，则轨道转移的脉冲施加位置也可分别采用变轨时刻和变轨点真近点角给出:

1)以变轨点真近点角θi表示脉冲施加位置.此时优化变量可表示为

式中Δt为最后两次脉冲的间隔时间，即Lambert变轨的转移时间.对轨道转移问题，不限制其到达终端轨道的时间，因此将Δt也作为优化变量，这与时间固定的交会问题有所不同.

2)以变轨点时刻ti表示脉冲施加位置.此时优化变量可表示为

式中Δθ为最后两次脉冲的间隔角距，即Lambert变轨的转移角度.对轨道转移问题，不限制其到达终端轨道的位置，因此将Δθ也作为优化变量.

综上，基于Lambert算法的多脉冲转移轨迹优化模型可描述为

对n脉冲轨道转移，共有n-1段转移轨道.实际任务中，航天器在某一段转移轨道上的停泊可能会超过一圈.此时需要通过设计变轨点真近点角θi或变轨时刻ti的范围来控制停泊圈数，对最后一段转移轨道，需要通过求解多圈Lambert问题［3］确定.

2 粒子群算法

2.1 算法基本模型

粒子群算法基于群体智能，采用全局搜索策略寻优.每个粒子根据全局最优位置和自身最优位置更新速度.粒子群算法相对遗传算法具有更加高效的信息共享机制，即启发性更强.因此，理论上粒子群算法收敛速度更快、全局搜索能力更强［9］.

设目标搜索空间为M维，粒子总数为I，总迭代次数为K.第i个粒子在M维空间的位置矢量为Xi=(xi1，xi2，…，xiM)，飞行速度矢量为 Vi=(vi1，vi2，…，viM)，第i个粒子的历史最优位置为 Pi=(pi1，pi2，…，piM)，全局历史最优位置为 Pg=(pg1，pg2，…，pgM).根据如下公式更新粒子速度和位置:

式中，w为惯性因子，c1，c2为加速因子(常数)，R1，R2，R3为［0，1］上的随机数.迭代中若xim，vim超出边界，则取边界值.为保证算法有较好的收敛性和搜索能力，可令w为随迭代次数变化的线性减小函数.对于该多脉冲转移优化问题，适应度函数F即目标函数Δv.

2.2 优化流程

每个优化变量的上下界可由轨道转移问题的动力学背景给出.同时采用式(10)模型获得的每个解均为可行解，因而不涉及等式或不等式约束处理.基于粒子群算法的优化流程如图2所示.

图2 粒子群算法流程图Fig.2 Flowchart of particle swarm optimization

1)设置粒子总数I和最大迭代次数K，设置航天器初始轨道要素E0和终端轨道要素Ef，优化变量上下界Dlow，Dup，根据式(11)第三式随机初始化各个粒子速度和位置，迭代次数k=1.

2)求解式(10)所示优化模型，获得变轨总速度增量，计算各个粒子适应度值.

3)对每个粒子，若其适应度值比当前个体极值更优，则更新当前个体极值;若其适应度值比当前全局极值更优，则更新当前全局极值.

4)根据式(11)前两式更新各个粒子速度和位置.

5)若k＜K，k=k+1.更新惯性因子，返回步骤2;否则，输出优化结果Δv、D或D'.

3 算例分析

首先基于本文建立的多脉冲轨道转移优化模型，分别对两脉冲、三脉冲轨道转移问题进行了优化求解，通过与解析解、现有文献研究结果对比，验证了优化模型和粒子群算法的正确性和高效性;其次分别采用变轨位置和变轨时间为设计变量，分析其对优化结果的影响.以下各算例均为单圈转移，Lambert问题采用式(2)求解.

3.1 两脉冲共面轨道转移

采用与文献［7-8］相同的两脉冲共面圆轨道转移算例.中心天体为火星 (μMars=4.283×104km3/s2)，初末轨道半径分别为r1=8 000 km，rF=15 000 km.该算例最优解为霍曼转移，最优总速度增量为 0.609 km/s［13］.

粒子群算法参数设置为:粒子总数15，最大迭代次数30，加速因子c1=2，c2=2，初始惯性因子w1=0.5，30次迭代时惯性因子w2=0.2.选用真近点角θ作为设计变量表示航天器变轨位置.优化变量的取值范围为:0≤θi≤2π(i=1，2)，0≤Δt≤30 000 s.

图3给出了迭代过程中目标函数的变化曲线，并将其与文献［7］中遗传算法的进化历史对比.由图3及表1可知，粒子群算法在前5代中迅速下降，通过30次迭代求得最优值为0.609 15 km/s，比遗传算法更快收敛到最小值，并得到了更优的结果，说明该算法具有较好的优化效率.

表1 粒子群算法与遗传算法优化结果比较Tab.1 Comparison of optimal two-impulse solutions obtained by PSO and GAs respectively

图3 粒子群算法进化历史Fig.3 Evolution history of particle swarm optimization

表2给出了粒子群算法优化得到的两脉冲轨道转移最优变轨位置和变轨脉冲.转移角度为179.97°，非常接近霍曼转移结果.图4给出了转移轨迹.

表2 最优变轨方案Tab.2 The optimal maneuver plan

图4 两脉冲转移轨迹Fig.4 Trajectory for two-impulse transfer

由于粒子群算法具有随机性，因此进行了50次仿真.将结果与文献［7］中遗传算法求得最优解比较，如表1所示，本文采用的粒子群算法优化结果更接近霍曼变轨.且相比遗传算法［7-8］，在相同迭代次数下粒子群算法使用粒子总数更少，获得最优解所需要的进化代数更少，计算目标函数的次数大大减少，因此具有更高的优化效率与优化性能.

3.2 三脉冲轨道转移

对三脉冲转移轨道，采用与文献［7］算例相同的初始条件和边界条件，中心天体为地球初始轨道和终端轨道为共面圆轨道，初末轨道半径分别为r1=8 000 km，rF=15 000 km.

当变轨次数n=3时，由式(10)可知，设计变量数为7.粒子群算法参数设置为:粒子总数30，迭代次数100，加速因子c1=2，c2=2，初始惯性因子w1=0.4 ，100 次迭代时惯性因子w2=0.2 .优化变量的取值范围为:0 ≤ θi≤ 2π(i=1，2，3)，0 ≤Δt≤86 400 s，-3 km/s≤Δv1i≤3 km/s(i=x，y，z).优化结果如表3所示.

对于此共面圆轨道转移，其最优解为霍曼转移.由图5和表3中数据可知，采用三脉冲转移模型求解该问题，施加两次脉冲后航天器已经转移至终端轨道，第三次速度增量接近0，也可认为是两脉冲转移.而前两次脉冲分别发生在第一转移轨道的近地点和远地点，即最优解仍为霍曼转移.

表3 三脉冲转移轨道优化结果对比Tab.3 Comparison of optimal three-impulse transfer solutions

图5 三脉冲转移轨迹Fig.5 Trajectory for three-impulse transfer

表3中给出了粒子群算法优化结果与文献［7］中遗传算法优化结果对比.可以看出，在迭代次数较少的情况下，粒子群算法最优解，更接近霍曼转移.

3.3 不同优化模型的影响分析

对于3.2中算例，使用式(10)中不同设计变量D，D'，各采用粒子群算法仿真100次，算法参数设置同3.2中算例.同时，统计不同设计变量下目标函数值下降到3.800 km/s时的平均迭代次数，结果如表4所示(霍曼转移最优解为3.770 725 km/s).

由于收敛速度与算法参数中粒子速度有关，这里把解的每一维粒子速度最大值都设为该维度解的区间长，以消除粒子速度的影响.由表4可知，对同一问题选用不同的设计变量，算法收敛速度和最优解会有所不同.以变轨点真近点角为设计变量时结果更优，收敛速度更快.

表4 不同优化模型结果对比Tab.4 Comparison of different optimization models

当选用变轨时刻为设计变量时，在转移轨道确定前，轨道周期是未知的，且不能确定航天器在轨运行圈数，故选取变轨点真近点角为设计变量更易实现.但在某些特殊情况下任务对转移时间有特定要求时，以变轨时刻为设计变量更合适.

4 结论

对于多脉冲轨道转移问题，本文建立了基于Lambert算法的可行解迭代优化模型，采用粒子群算法进行求解，并对分别采用变轨点真近点角和变轨时刻作为设计变量的优化结果进行了对比分析.算例分析表明:1)本文基于粒子群算法的多脉冲转移轨迹优化模型合理可行，优化结果更优，效率更高;2)当采用真近点角表示航天器位置时，算法更易实现，优化结果更优.

［1］GOBETZ F W，DOLL J R.A survey of impulsive trajectories［J］.AIAA Journal，1969，7(5):801-834.

［2］杨嘉墀.航天器轨道动力学与控制(下)［M］.北京:宇航出版社，2002:61-137.

［3］唐国金，罗亚中，雍恩米.航天器轨迹优化理论、方法及应用［M］.北京:科学出版社，2012:167-195.

［4］PRUSSING J E，CHIU J H.Optimal multiple-impulse time-fixed rendezvous between circular orbits［J］.Journal of Guidance Control and Dynamics，1986，9(1):17-22.

［5］HUGHES S P，MAILHE L M，GUZMAN J J.A comparison of trajectory optimization methods for the impulsive minimum fuel rendezvous problem ［J］.Advances in the Astronautical Sciences，2003，113:85-104.

［6］LUO Y Z，TANG G J，LEI Y J，et al.Optimization of multiple-impulse multiple-revolution rendezvous phasing maneuvers［J］.Journal of Guidance，Control and Dynamics，2007，30(4):946-952.

［7］ABDELKHALIK O，MORTARI D.N-impulse orbit transfer using genetic algorithms［J］.Journal of Spacecraft and Rockets，2007，44(2):456-460.

［8］ABDELKHALIK O.Orbit design and estimation for surveillance missions using genetic algorithms［D］.Austin:University of Texas，2005.

［9］KENNEDY J，EBERHART R.Particle swarm optimization［C］//IEEE International Conference on Neural Networks.New York:IEEE，1995:1942-1948.

［10］ZHU K J，JIANG F H，LI J F，et al.Trajectory optimization of multi-asteroids exploration with low thrust［J］.Transactions of the Japan Society for Aeronautical and Space Sciences，2009，52:47-54.

［11］PONTANI M，GHOSH P，CONWAY B A.Particle swarm optimization of multiple-burn rendezvous trajectories［J］.Journal of Guidance，Control，and Dynamics，2012，35(4):1192-1207.

［12］VALLADO D A.Fundamentals of astrodynamics and applications［M］.2nd ed.EI Segundo，California:Microcosm Press，2001:303-395.

［13］BROWN C D.Spacecraft mission design［M］.2nd ed.Washington D.C.:AIAA，1998:39-51.