类X-20高超声速飞行器反馈线性化控制研究*

龚宇莲，孟 斌

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

0 引言

近年来，由于在航空航天任务中的广泛应用前景，高超声速飞行器的建模和控制问题得到很多学者的关注［1］.高超声速飞行器与亚声速/超声速飞行器相比有许多不同的飞行特性，有的方面目前还无法完全掌握，使得高超声速动力学呈现强不确定性.飞行器飞行过程中的各种复杂的动力学过程不可能完全精确地考虑在用于控制设计的飞行器控制模型中，而且飞行过程中往往又会受到各种无法完全预知的扰动，这些因素直接导致了高超声速飞行器控制系统的基础结构失真、模型和参数的不确定性，使得高超声速飞行器的控制问题非常具有挑战性.近年来，国内外许多学者对高超声速飞行器的建模和控制问题展开了大量研究，取得了不少成果［2-5］.但是，由于公开发表的气动数据不足，高超声速飞行器的控制问题的研究一般是针对纵向动力学的［1］.

国内研究团队参照美国X-20飞行器构造的飞行器外形，称为“类X-20飞行器”，利用工程快速计算方法对类X-20飞行器进行了气动建模，给出了高度为20～80 km，Ma为5～25的气动数据.通过与数值建模结果比较分析可知，工程快速计算方法可以较好地模拟高超声速飞行器的飞行动力特性，为高超声速飞行器的控制研究提供了基础［6］.本文研究类X-20飞行器基于反馈线性化的控制设计问题.反馈线性化控制方法一般要求被控对象的动力学满足一定的相对阶条件，并且具有仿射非线性的特点.但是类X-20飞行器的各项气动数据没有相应的解析表达式，反馈线性化控制的设计具有一定难度.针对上述问题，首先对气动系数与高度、攻角、侧滑角和舵偏角的关系进行了深入分析，进而对气动系数按照各自变量的变化进行了简化和拟合，并将舵偏增量视作控制设计变量，在此基础上建立了类X-20飞行器仿射非线性形式的控制模型，并证明了它是可以输入输出精确线性化的，从而可以设计反馈线性化控制器.在存在大气密度、气动力矩系数和转动惯量不确定性情形下，针对原动力学模型进行了仿真研究，原动力学模型考虑地球旋转，气动数据直接从类X-20飞行器的气动数据表插值得到.仿真结果表明，所设计的控制律可以实现控制目标，具有较强鲁棒性.

1 问题描述

本文研究的类X-20飞行器(如图1所示)，具有4个独立的控制舵面，即左、右副翼和左、右方向舵.两个副翼同步偏转时，主要产生俯仰通道的控制力矩;两个副翼差动偏转时，主要产生滚动通道的控制力矩;两个方向舵同步偏转时，主要产生偏航通道的控制力矩.

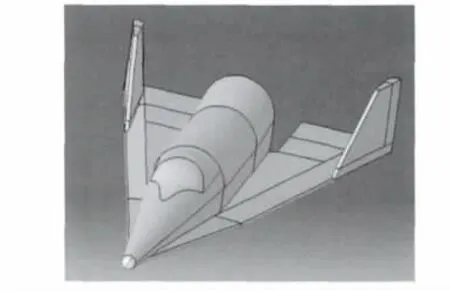
图1 飞行器外形示意图Fig.1 Configuration of the vehicle

针对文献［7］中旋转圆形地球情形下的飞行器动力学模型，利用攻角和侧滑角与飞行器速度的关系，可以得到飞行器以攻角和侧滑角描述的六自由度动力学方程.在再入过程中，高超声速飞行器侧滑角保持在0°附近.忽略地球旋转角速度和飞行器本体系绕惯性系旋转角速度，在β≈0时，高超声速飞行器的姿态动力学模型为

式中，ω=［ωxωyωz］T为机体系三轴旋转角速度，M=［MXMYMZ］T为三轴气动力矩，Qx，Qy，Qz为三轴气动力.为飞行器惯量阵.m为飞行质量，α，β，φ，θ分别为攻角、侧滑角、滚转角以及俯仰角，γ为爬长角，H、V、g分别为高度、速度以及重力加速度.其中气动力与气动力矩表达式如下:

式中，ρ为大气密度，lt和St分别为飞行器参考长度和参考面积，各项气动系数均建模为基本量和由舵偏产生的气动系数增量的和［6］，具体形式如下:

式中，Ci包括Ca，Cy，Cmx，Cmy，Cmz分别表示轴向、侧向、法向力系数以及三轴力矩系数.Ci0表示气动系数基本量，是H，Ma，α，β 的函数，ΔCi，j表示由舵j产生的相应气动系数Ci的增量，是H，Ma，α，β和舵j的函数，δe，δr，δφ分别表示俯仰、偏航和滚动舵偏角.

本文控制目标为存在大气密度、气动系数和转动惯量不确定性下，跟踪攻角和滚转角曲线，并使侧滑角保持在0°附近.飞行器姿态跟踪曲线通过制导律得到，详见文献［8］.

2 控制模型和基于反馈线性化的控制

上一节建立了类X-20飞行器的气动模型(3)，各项气动系数是高度、马赫数、攻角、侧滑角以及舵偏角的复杂非线性函数.为了设计基于反馈线性化的控制律，需要建立其仿射非线性形式的解析数学模型.本文直接给出气动系数与各自变量关系的拟合结果，拟合过程分析参见文献［8］.

从文献［8］可知，本文主要用到攻角为15°左右时的气动力矩系数，并且再入时侧滑角保持在0°附近.因此本文仅给出当攻角为15°和侧滑角为0°时的拟合函数，具体如下:

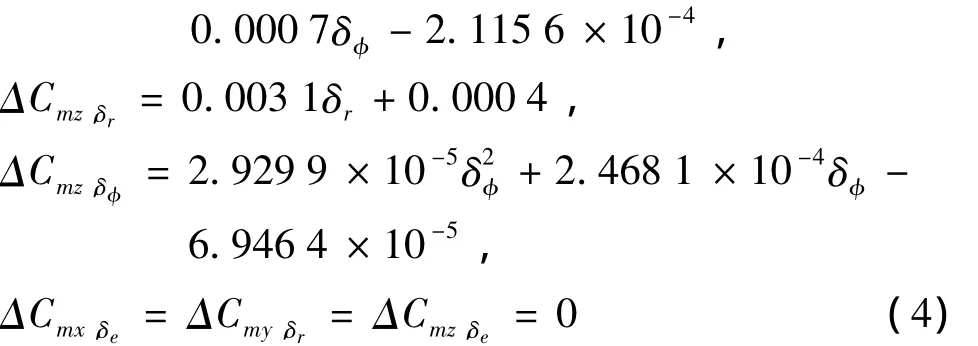
联合式(1)～(4)，可以得到类X-20飞行器的解析模型.但从式(4)可以看出，所建立的解析模型是舵偏角的高阶非线性函数，因此，本节进一步对式(4)进行简化，将舵偏角增量视作控制输入，建立了类X-20飞行器的仿射非线性形式的控制模型，并证明了它是可以输入输出线性化的，在此基础上设计了基于反馈线性化的控制律.

将力矩系数随舵偏角的增量函数(4)用一阶泰勒展式近似如下:

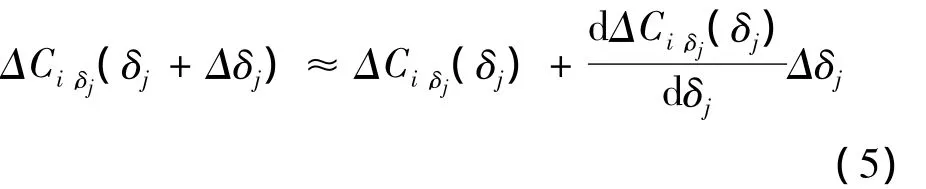
式中:i为mx，my，mz;Δδj为 Δδe，Δδr，Δδφ;Δδj表示相应舵偏角增量;将式(2)、(4)和(5)代入式(1)，可得:

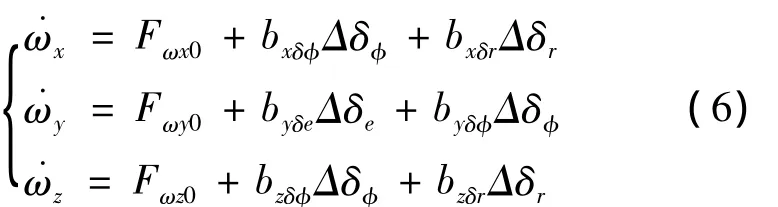
其中:

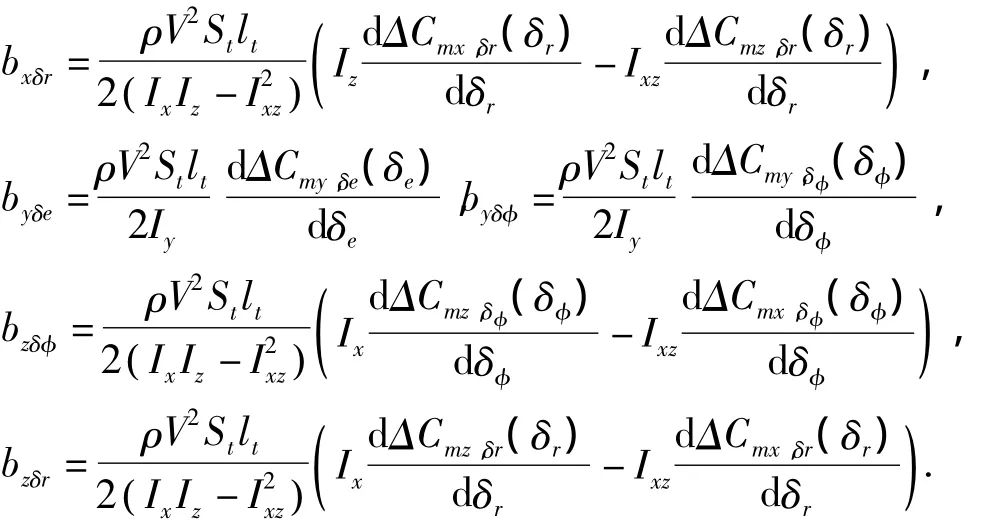
通过式(5)的变换，将舵偏角视作系统的可变参数，舵偏角的增量作为控制设计输出量.结合式(1)、(6)，建立了类X-20飞行器的仿射非线性形式的控制模型，其状态X、输入U和输出Y分别为X=［α β φ ωxωyωz］T， U=［ΔδeΔδrΔδφ］T，Y=［α β φ］T，其中各项气动系数由式(4)计算.下面计算控制模型的相对阶.分别记式(1)中右边的非线性函数为Fα、Fβ和Fφ.对输出Y求二阶导数，可得:

将式(6)代入式(7)，可得:

其中，

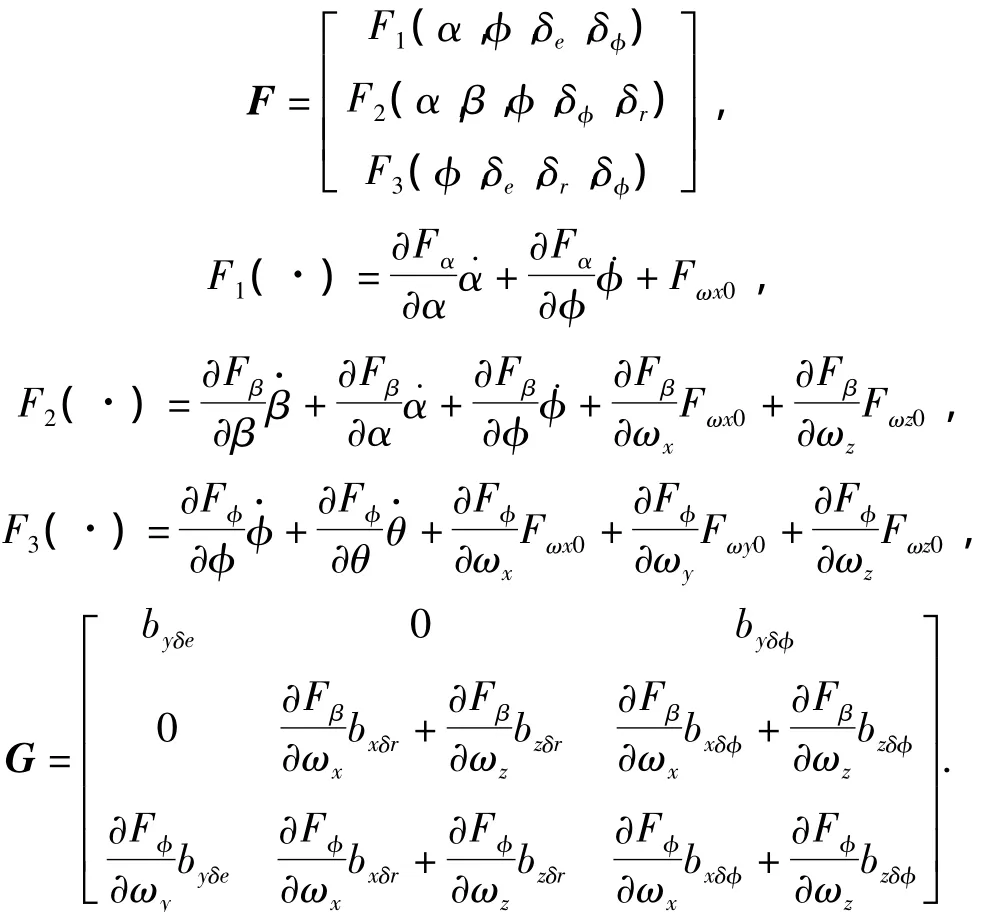
通过对矩阵G仿真和数值分析可知，矩阵G在整个飞行过程中均为非奇异矩阵，因此所建立的仿射非线性方程的相对阶为{2，2，2}，也是可以输入输出线性化的.按照反馈线性化控制设计方法，可以设计姿态角跟踪控制律如下:

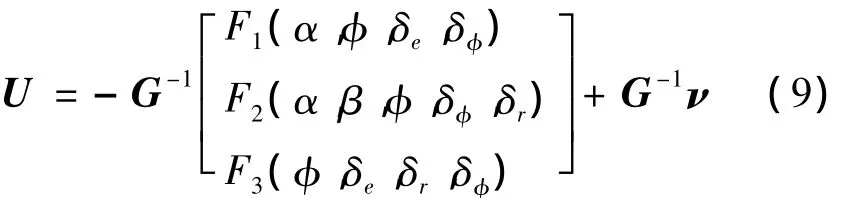
3 基于原动力学模型的仿真

本节针对类X-20飞行器的原动力学模型，在存在大气密度、转动惯量和气动系数不确定性情形下，设计控制律(9)，考察其鲁棒性和可行性.原动力学模型考虑圆形旋转地球动力学［7］，其中各项气动系数模型如式(3)所示，具体数据由类X-20飞行器的气动数据表插值得到.在仿真中，为了降低在跟踪指令跳变时刻的超调，利用一阶环节对跟踪指令进行柔化滤波，所设计的滤波环节如下:

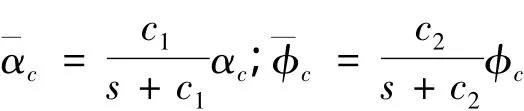
式中，c1、c2为设计常数，与为滤波后的姿态角跟踪指令.仿真初始条件为H=60 km，γ=0，V=6 000 m/s，航迹方位角 χ=90°，攻角、侧滑角、滚转角的初值都为0.舵偏角的绝对值限幅为30°，控制系统如图2所示.

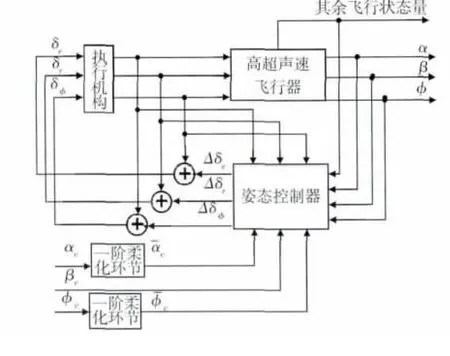
图2 控制系统框图Fig.2 Diagram of control system

分别在标称情形和存在不确定性的情形下进行仿真.标称情形虽然不考虑各参数的不确定性，但是由于原动力学模型的气动系数直接由气动系数表插值得到，而控制器(9)是利用拟合气动参数(4)进行设计的，因此在标称情形仍存在气动系数偏差带来的不确定性.标称情形的仿真结果如图3～6所示.图3为1 000s飞行过程的仿真结果，图4和图5分别列出了飞行器控制初始段和滚转角第一次跳变处的姿态角变化情况，图6为飞行器稳态跟踪误差曲线.

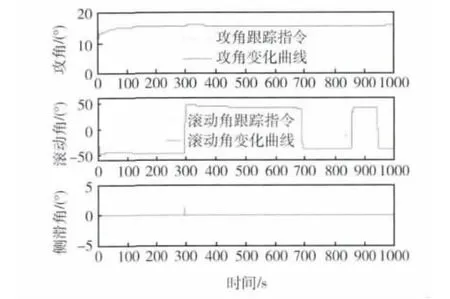
图3 姿态角全过程变化曲线Fig.3 Attitude angle profile during the whole flight envelop

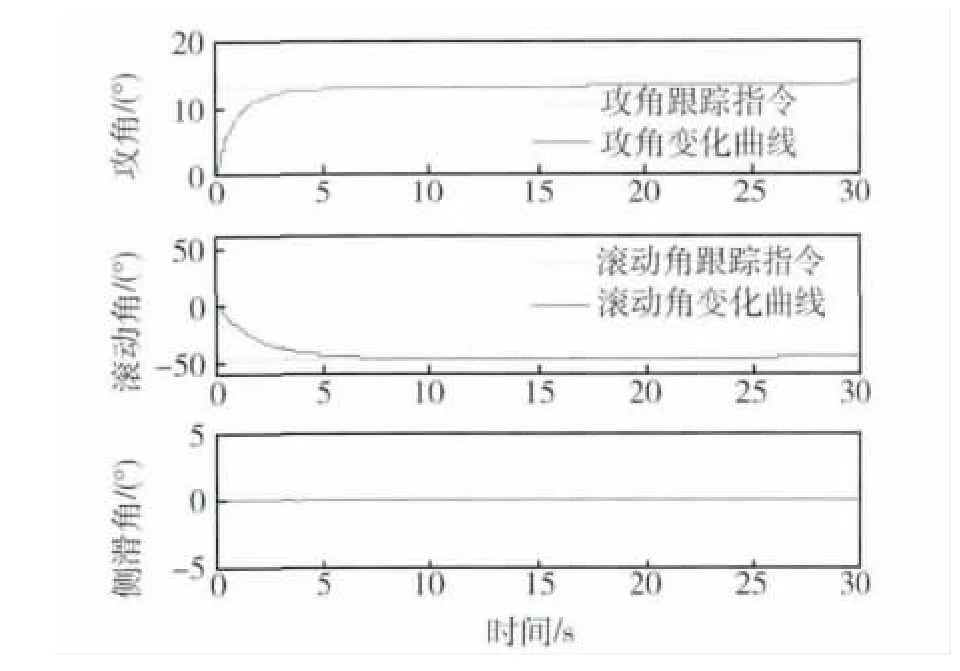
图4 初始段姿态角变化曲线Fig.4 Attitude angle profile at the initial phase

为验证控制器的鲁棒性，数学仿真中考虑大气密度、气动力矩系数30%的偏差，主轴惯量以及惯量积10%的偏差作遍历仿真，结果显示控制算法能适应较大的偏差条件.本文给出一组不确定性情形下的仿真结果，大气密度、气动力矩系数和转动惯量的不确定性建模如下:

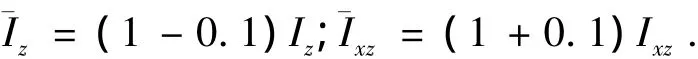
图5 滚转角指令跳变处姿态角变化曲线Fig.5 Attitude angle profile when the roll angle command skips

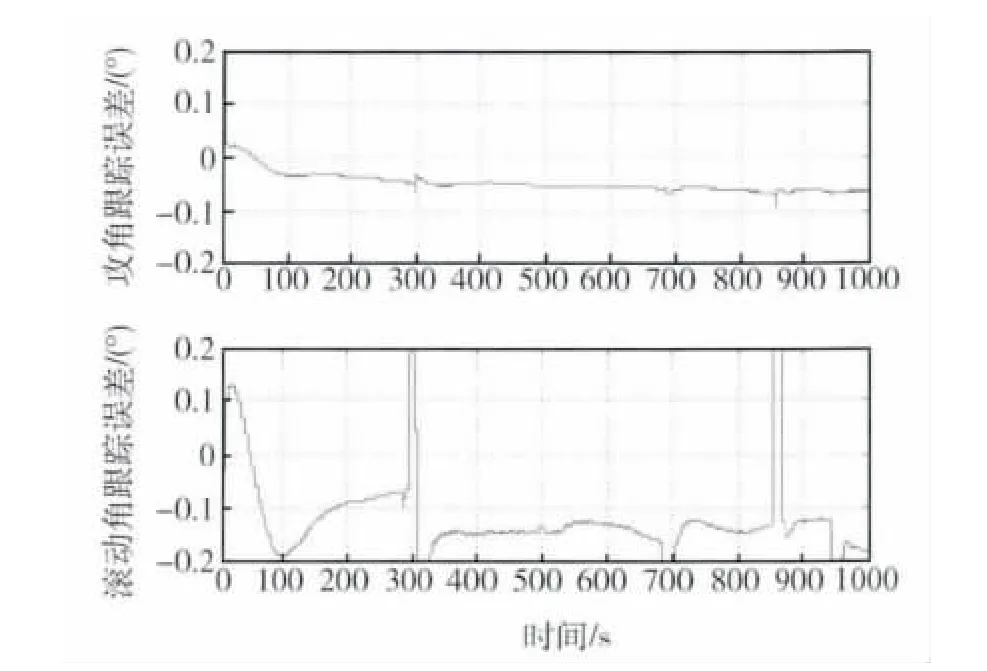
图6 攻角、滚动角跟踪误差曲线Fig.6 Track errors of angle of attack and roll angle

仿真结果如图7～10所示.从仿真结果可以看出，所设计的控制律可以实现控制目标，具有较强的鲁棒性.

图7 参数不确定性下姿态角变化曲线Fig.7 Attitude angle profile with parameter uncertainty

图8 参数不确定下初始段姿态角变化曲线Fig.8 Attitude angle profile at the initial phase with parameter uncertainty

图9 参数不确定下滚转角指令跳变处姿态角变化曲线Fig.9 Attitude angle profile when the roll angle command skips with parameter uncertainty

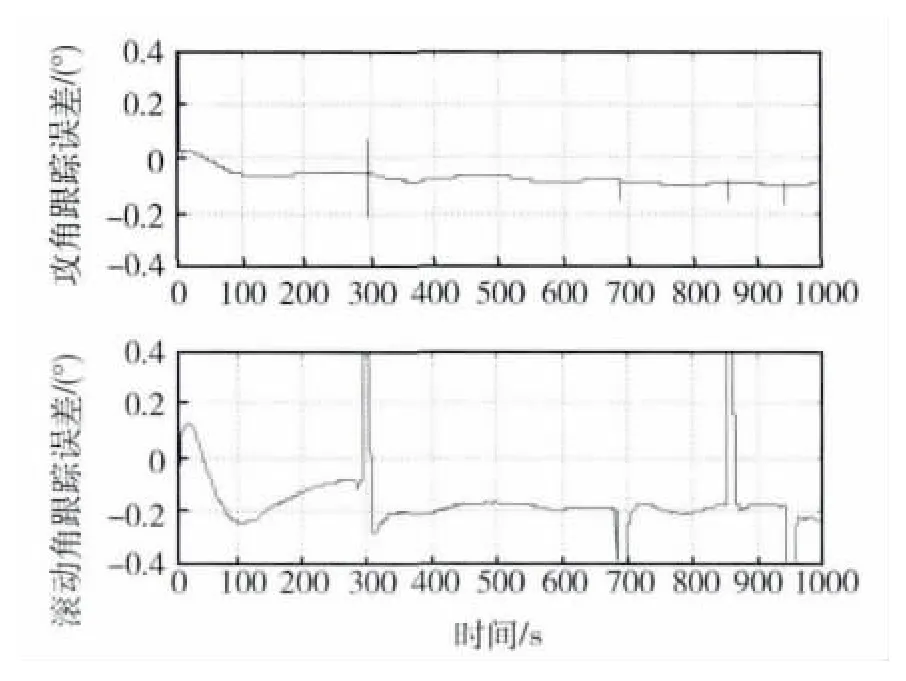
图10 参数不确定性下姿态角跟踪误差曲线Fig.10 Track errors of angle of attack and roll angle with parameter uncertainty

4 结论

本文给出了类X-20高超声速飞行器的气动系数与各自变量的关系，在此基础上进行了简化和拟合，并将舵偏增量视作控制输入，建立了飞行器仿射非线性形式的控制模型.针对该控制模型，通过分析可知它是可以输入输出精确线性化的，从而可以设计反馈线性化控制器.最后在存在不确定性情形下对原动力学模型进行了数学仿真.仿真结果表明，所设计的控制律可以实现控制目标，具有较强鲁棒性.

［1］吴宏鑫，孟斌.高超声速飞行器控制研究综述［J］.力学进展，2009，39(6):756-765.WU H X，MENG B.Review on the control of hypersonic flight vehicles［J］.Advances in Mechanics，2009，39(6):756-765.

［2］FIORENTINI L，SERRANI A，BOLENDER M A，et al.Nonlinear robust/adaptive controller design for an air-breathing hypersonic vehicle model［R］.Washington D.C.:AIAA，2007.

［3］SIGTHORSSON D O，JANKOVSKY P，SERRANI A，et al.Robust linear output feedback control of an airbreathing hypersonic vehicle［J］.Journal of Guidance，Control，and Dynamics，2008，31(4):1052-1066.

［4］WANG J，WANG Q，AI J L.Dynamic inversion-based control system of a hypersonic vehicle with model uncertainty［R］.Washington D.C.:AIAA，2012.

［5］SHAKIBA M，SERRANI A.Control oriented modeling of 6-DOF hypersonic vehicle dynamics［R］.Washington D.C.:AIAA，2011.

［6］张红军，陈英文，张卫民.基于工程快速计算方法的高超声速高升阻比飞行器气动特性研究［J］.战术导弹技术，2011(1):37-43.ZHANG H J，CHEN Y W，ZHANG W M.Research on aerodynamics characteristic of hypersonic high lift-drag ratio vehicle based on engineer rapid prediction method［J］.Tactical Missile Technology，2011(1):37-43.

［7］肖业伦.航空航天器运动的建模［M］.北京:北京航空航天大学出版社，2003:38-51.

［8］龚宇莲.特征模型在高超声速飞行器控制中的应用研究［D］.北京:北京控制工程研究所，2010.GONG Y L.Research on the hypersonic flight vehicle control based on the characteristic model theory［D］.Beijing:Beijing Institute of Control Engineering，2010.