基于高度跟踪的末端能量管理段制导*
2014-05-06句美琪何英姿
句美琪,何英姿,2
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
0 引言
本文研究的可重复使用飞行器采用类似飞机的面对称构型,具备水平滑行着陆的能力.对此类飞行器来说,由于没有动力,要实现水平着陆,其难度大于普通的飞机.此类飞行器典型的再入飞行包含3个阶段:初期再入段,末端能量管理段(TAEM,terminal area energy management)以及进场着陆段[1].
末端能量管理段作为再入飞行的一段,是连接初期再入与进场着陆段的关键阶段,是飞行器无动力返回的核心技术,也是保证进入着陆窗口的关键技术.末端能量管理系统通过能量-待飞距剖面对飞行器实施制导[2],并对能量加以控制,引导飞行器到达安全的着陆窗口(ALI,approach and landing interface).
美国的航天飞机起步早,发展已经比较成熟.在20世纪70年代,大量学者纷纷投入到末端能量管理段的制导方法的研究中.1975年航天飞机综合备选方案的优点,采用了“混合基准”(hybrid baseline)方案[3].
“混合基准”方案纵向制导采用分段制导跟踪能量和高度,本文纵向制导上采用高度进行控制,制导律更为简单、直接,根据系统线性化和退步设计生成纵向反馈指令.
本文首先建立基于高度的质点动力学方程,完成离线的二维轨迹优化设计方案.根据航程的需要,调整动压剖面,迭代更新标称的能量、高度、速度剖面,完成攻角前馈指令的生成;再加入攻角和倾侧角在线生成指令完成了整个控制回路的设计.最后完成三自由度仿真,进行了多组误差仿真,验证了算法的有效性和鲁棒性.
1 数学模型
在忽略侧向力的情况下建立质点运动模型.由于飞行器在末端能量管理段的飞行马赫数、高度、航程均较小,地球自转和地球曲率对其影响很小,因此,不考虑地球曲率和自转的影响.飞行器的三自由度质点动力学方程如下[2,4]:

式中:g=9.8 m/s2;h,x,y,V,γ,ψ,m分别表示飞行器质心的海拔高度,质心在地面坐标系下的纵向、横向坐标,飞行器速度,航迹倾向航向偏角,飞行器质量,φ表示倾侧角.方程中的角度统一使用弧度.
D和L表示阻力和升力,其表达式为

式中,S为参考面积,Cd,Cl分别为阻力系数,升力系数,通过对攻角和马赫数的插值得到.
动压的定义为

式中ρ为大气密度.本文采用的大气模型是美国标准大气(1976)[5],并在此基础上考虑偏差.
2 TAEM段对制导系统的要求
本文设计飞行器从海拔30 km高度降至海拔4 km高度,对它的能量(动能和势能)进行控制,为飞行器自动着陆段提供良好的初始状态[6].由再入制导分析计算可得到在末端能量段制导开始时飞行器的状态参数及其3 σ偏差,考虑此时的标称飞行参数为高度30 km,Ma=2.5,航向角指向着陆起始点,航迹倾角 -3.3°.
对TAEM制导系统的具体要求如下:1)当飞行器再入结束时状态变量有一定偏差时仍能实施控制.对本文研究的飞行器需要考虑的初始误差散布包括高度散布和速度散布.2)在大气密度偏差或气动模型偏差时系统仍能工作,并且在飞行过程中不超过对飞行器的约束条件,典型的包括法向过载约束和动压约束.
3 TAEM制导律设计
标称制导[7]指令是依据规划的地面轨迹、纵向高度、速度剖面离线生成的,由于实际飞行过程中存在各类摄动及不确定因素,飞行器仅仅跟踪标称的制导指令[8-9]的精度很低,必须根据实时跟踪误差进行反馈控制,加入反馈制导指令.首先,混合基准方案中,纵向制导跟踪标称能量曲线,最后才对高度进行控制,本文则只选取高度为纵向跟踪控制量,简化了整个纵向制导律的设计.其次,本文采用反馈线性化原理和退步原理设计的反馈控制系数.
3.1 纵向制导律设计方法
飞行器纵向需对高度进行控制.对于高度,采用比例加微分控制,根据高度误差信号调整攻角大小.为了使控制系统具备良好的性能指标所期望跟踪误差是一个二阶振荡系统[10],即

基于系统反馈线性化原理和退步原理,攻角的反馈指令由高度偏差生成:

由式(1)可得:
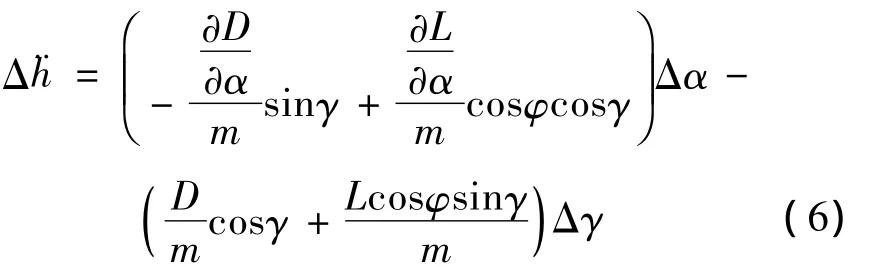
式(4)、(5)和(6)联立整理可得

其中,△α为实际攻角控制量与参考攻角的差值,△h为实际飞行高度与标称高度的差值.ξ一般取为0.8,ω根据飞行器实际能力确定,本文中取为0.08.
由于此方法得出的结果与飞行器的实时状态相关,计算较为复杂,因此结合TAEM段的弹道特性,将设计参数简化为根据速度调度的常数增益,方便工程上的应用:

3.2 横侧向制导律设计方法
忽略飞行器纵向和横侧向之间的耦合作用,横侧向指令根据飞行过程实时生成.本文飞行器的地面轨迹采用“混合基准”方案,图1给出了轨迹规划的分段。

图1 混合基准方案的分段Fig.1 Hybrid baseline schema
航向捕获段采用比例控制,根据速度方向与当前位置和航向校正圆(HAC,heading alignment cylinder)圆切线的角度误差调整倾侧角大小.倾侧角指令可以是航向偏差的函数,如下所示:

式中:ΔψAC为速度方向与当前位置和HAC圆切线的角度差,k1为设计参数.
与纵向制导律设计方法相同,航向校正段采用比例和微分控制,根据当前飞行器的地面投影位置与HAC圆心的距离和HAC半径的长度差调整倾侧角大小.为使跟踪误差时一个二阶振荡系统,所以倾侧角指令为

式中,ΔR为对航向校正圆柱/圆锥的偏差.
航向校正段采用的固定校正圆,因此可以将设计参数简化为

进场前飞行段采用比例加微分控制,根据当前飞行器的地面投影与跑道的垂直距离调整倾侧角大小.倾侧角指令为
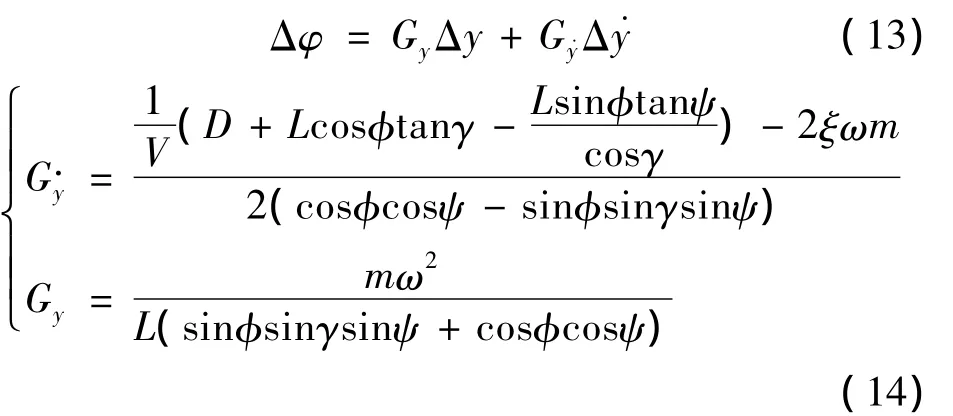
式中Δy为当前飞行器在地面的投影与跑道的x方向上的距离.
结合TAEM段的弹道特性,将上述参数设计简化为

4 仿真算例
图2~7给出初始状态无偏差,气动参数理想情况下时的仿真结果:最终高度4 012.11 m;速度145.50 m/s;航向角 -3.51°,航迹倾角 -13.24°;地面投影坐标(0.007,-0.084).以 ALI点为坐标原点.

图2 动压随时间变化曲线Fig.2 Dynamical pressure along time

图3 航迹倾角随时间变化曲线Fig.3 Flight path angel along time

图4 过载随时间的变化Fig.4 A curve about overload along time
整个飞行过程满足过程约束并且终端结果满足自动着陆段对初始状态的需求.
对于初始高度(±2 km),初始速度(Ma=±0.2),质量特性(±5%)以及气动参数(±10%ρ,±5%Cd,±5%Cl)存在单项误差,以及气动参数(-5%Cd、+5%Cl和 +5%Cd、-5%Cl)均有误差的情况进行了仿真.其结果如表1所示.

图5 攻角随时间变化曲线Fig.5 Angel of attack along time
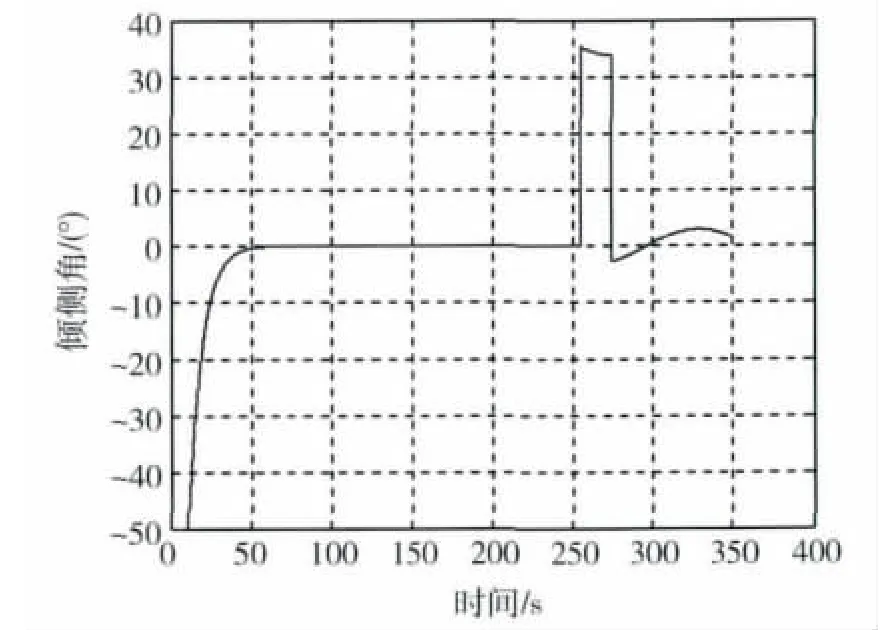
图6 倾侧角随时间变化曲线Fig.6 Bank angel along time
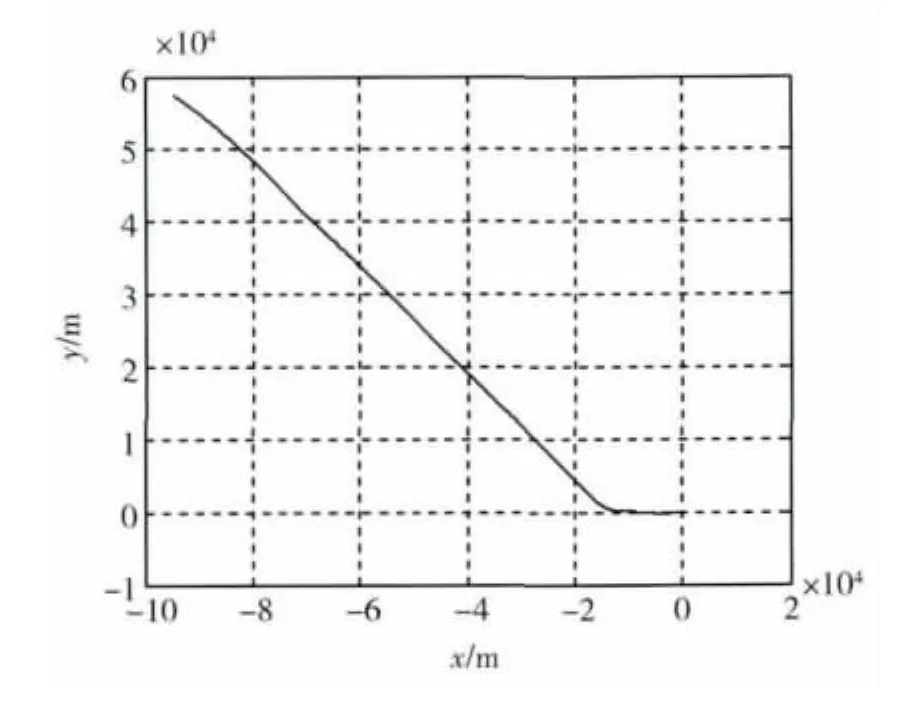
图7 地面轨迹Fig.7 Ground trace

表1 不同误差情况下的仿真结果Tab.1 The simulation results with different errors
比较以上仿真结果可知,对于初始能量状态存在一定范围内的偏差和气动模型存在一定误差,飞行器最终都能到达跑道上方,并且满足着陆窗口要求和过程要求,安全完成末端能量管理段飞行,具有较强的鲁棒性.
5 结论
本文在航天飞机“混合基准”制导方案的基础上,对纵向制导律的设计和控制参数的设计上进行了改进,为了方便工程应用,给出了简化的控制参数设计.
通过对存在初始高度、速度、质量偏差、大气密度偏差、气动系数偏差的情况下进行数学仿真,结果显示该方法具有一定的鲁棒性和有效性.
该控制参数的算法简单,并且能够适应一定范围的初始能量状态变化和模型不确定性,具有较强的工程实用性.
[1]RIDDER S D,MOOIJ E.Optimal terminal-area strategies and energy-tube concept for a winged re-entry vehicle[R].Washington D.C.:AIAA,2009.
[2]赵汉元.飞行器再入动力学和制导[M].长沙:国防科技大学出版社,1997:48-98.
[3]THOMAS E M.Space shuttle entry terminal area energy management[R].Washington D.C.:NASA Johnson Space Center,1991.
[4]HOMEMAN K R.Terminal area energy management trajectory planning for an unpowered reusable launch vehicle[R].Washington D.C.:AIAA,2004.
[5]李惠峰.高超声速飞行器制导与控制技术(上)[M].北京:宇航出版社,2012:897-908.
[6]杨嘉墀.航天器轨道动力学与控制(下册)[M].北京:宇航出版社,1995:315-320.
[7]孙春贞,黄一敏,郭锁凤.重复使用运载器末端能量管理段轨迹线设计[J].系统工程与电子技术,2007,29(6):909-914.SUN C Z,HUANG Y M,GUO S F.Trajectory design for terminal area energy management of reusable launch vehicle[J].Systems Engineering and Electronics,2007,29(6):909-914.
[8]沈宏良,龚正.航天飞机末端能量管理段在线轨迹设计方法[J].宇航学报,2006,29(2):430-433.SHEN H L,GONG Z.Methodology of onboard trajectory design for space shuttle terminal area energy management phase[J].Journal of Astronautics,2006,29(2):430-433.
[9]李娜.一种RLV末端能量管理段的轨迹实时规划方法[J].装备指挥技术学院学报,2011,22(4):72-76.LI N.A design method of on-line trajectory planning for RLV terminal area energy management phase[J].Journal of the Academy of Equipment Command&Technology,2011,22(4):72-76.
[10]李强.一种基于解析规划的多约束再入制导算法[J].弹箭与制导学报,2013,33(1):1-9.LI Q.Reentry guidance research with multi-constrain based on analytic planning method[J].Journal of Projectiles,Rockets,Missiles and Guidance,2013,33(1):1-9.
