飞轮轴承润滑最佳油量的估算方法及实验验证*
2014-05-06周宁宁
吴 博,卿 涛,周宁宁
(北京控制工程研究所,北京100190)
0 引言
飞轮、控制力矩陀螺等空间机构是航天器姿态控制分系统的核心部件,这类机构通常以轴承为支撑,轴承的润滑状态、寿命和可靠性在很大程度上决定了航天器的运转精度、寿命和可靠性[1-2].飞轮轴承的润滑表现为微量油润滑,一方面,轴承沟道内润滑油过多,则由于润滑油粘滞阻力的变化,造成轴承摩擦力矩增大和保持架不稳定;另一方面,润滑油不足,则乏油润滑将使轴承滚珠和沟道直接接触,增加摩擦和磨损.两者均会导致轴承寿命的降低和轴承摩擦力矩的增大最终导致飞轮姿控能力和寿命的下降.因此,轴承润滑油量存在一个范围使得轴承在弹流润滑状态下摩擦力矩最低,即轴承的润滑最佳油量.
由于弹流润滑状态时两摩擦副基本无接触运动,磨损几乎不发生,因此,轴承润滑最佳油量理论上为轴承滚珠和沟道恰好形成弹流润滑油膜时沟道内润滑油量.本文基于弹流润滑理论,提出了一种估算轴承最佳润滑油量的理论计算方法,并利用真空摩擦磨损实验机上开展球-盘摩擦副实验,验证了提出的轴承润滑最佳油量理论计算方法的准确性.
1 理论分析
1.1 模型描述
飞轮用油润滑精密角接触球轴承滚珠和沟道接触为点接触,飞轮正常工作时轴承滚珠和沟道润滑问题为点接触弹流润滑问题,把影响点接触弹流润滑的油量均看作润滑最佳油量的一部分,轴承润滑最佳油量由4部分组成:(1)轴承滚珠和沟道接触区内形成弹流润滑油膜的润滑油量;(2)轴承滚珠和沟道间弹流润滑油膜不足1 μm,由于毛细力作用,在轴承滚珠和沟道间产生润滑油弯液面,润滑油弯液面的润滑油量;(3)材料表面形貌影响,填满滚珠和沟道表面凹谷的润滑油量;(4)接触入口区的位置和供油油量影响接触区润滑膜厚,恰好形成弹流润滑膜接触入口区润滑油量.根据以上4部分建立的润滑最佳油量模型如图1所示.

图1 轴承润滑最佳油量模型Fig.1 Model of the optimum lubricating oil quantity in bearing
图1中,x为轴承滚珠运动方向,l为弯液面到接触区中心的距离,r为弯液面半径,a为赫兹接触椭圆半长轴,h0为中心油膜厚度,δ为弹性趋近量,R为滚珠半径.
根据赫兹接触理论可知,轴承滚珠和沟道接触区椭圆长短半轴a、b及弹性趋近量δ为[3]
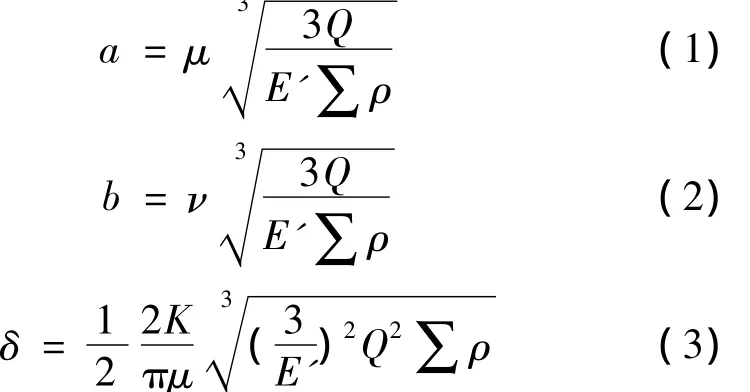
式中,μ、ν、K为相关椭圆积分;∑ρ为滚珠和沟道
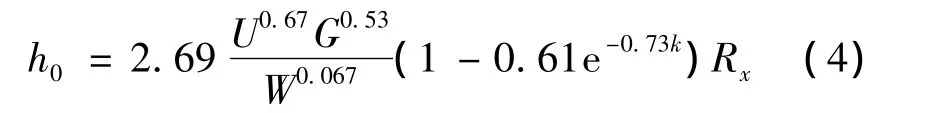
式中,U、G、W为无量纲参数,分别表示速度参数、材料参数、载荷参数;k为椭圆率;Rx为滚珠运动方向当量曲率半径.
1.2 润滑最佳油量分析
基于以上模型和关系式,逐一分析润滑最佳油量4个组成部分,得到飞轮轴承润滑最佳油量.
(1)弹流润滑膜油量
赫兹接触区内润滑膜厚基本保持不变,称为中心油膜厚度.轴承滚道内滚珠经过区域分布一层厚度为中心油膜厚度的润滑油量为弹流润滑膜油量.

弹流润滑膜油量为单个椭圆接触区润滑油量沿内/外圈积分,即接触处主曲率和;E'、Q分别表示材料当量弹性模量和接触点法向载荷.
根据弹流润滑理论[4]可知,轴承沟道与滚珠接触的中心油膜厚度为
式中,ρ为润滑油密度;D为轴承滚珠与内(外)圈接触处直径,下标i(e)表示轴承内(外)圈;h0表示中心油膜厚度.
(2)润滑油弯液面油量
轴承滚珠个数为Z,滚珠在内/外沟道各形成Z个接触区,润滑油弯液面的润滑油量为

式中,Vi(e)为弯液面、滚珠、沟道、接触区形成的区域体积.设Si(e)为接触区长轴与滚珠中心-沟道中心组成的径向平面截Vi(e)的面积,即图1中阴影部分.

其中

式中,z方向积分从沟道圆到滚珠圆;f为沟曲率半径系数,f=r/2R;R为轴承滚珠半径;l为弯液面起始点位置到接触区中心的距离,l≈2a.
(3)表面形貌影响的油量
真实表面不可能绝对光滑,在显微镜下能观察到材料表面因加工造成的许多不规则的凸峰和凹谷,切削加工表面的轮廓高度接近于高斯分布规律[4],填满这些凹谷所需要的润滑油量为

式中Ra1、Ra2为滚珠和沟道表面粗糙度,S1和S2为滚珠-沟道摩擦副在滚珠和沟道表面的名义接触面积.
(4)接触入口区油量
润滑接触区成膜与上游边界位置和油量有关,上游边界位置太靠近接触区润滑膜会变薄,把这种润滑状态称为乏油弹流润滑[5-6].当供油油膜达到一定数值,接触区膜厚基本不变.过量供油,多余润滑油不能进入接触区,因此并不改善润滑状态[7-8].设当供油量达到一定数值,接触区膜厚基本不变时,此时压力入口区位置xsta,供油膜厚hoil,接触入口区润滑油量为

因此,飞轮轴承润滑最佳油量为

2 实验研究
2.1 实验条件及方案
用真空多功能型摩擦磨损试验机开展球-盘摩擦副验证实验,球用飞轮轴承滚珠,滚珠直径6 mm,滚珠精度等级为G5,表面粗糙度0.012 μm,盘的材料为与飞轮轴承套圈材料相同的9Cr18Mo,盘表面粗糙度0.04 μm.润滑油选用某型号空间精密轴承润滑油,经测定40℃运动粘度约为60 mm2/s.
如图3所示安装好清洗好的球盘实验件,设定旋转半径、载荷、驱动转速,实验时间后开始实验.
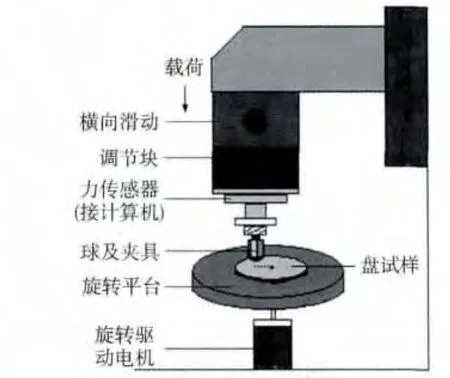
图2 球-盘实验装置示意图Fig.2 Ball-on-disk test apparatus
在研究载荷、速度对球-盘摩擦副摩擦学性能影响基础上,开展不同添加油量的球-盘摩擦副摩擦学性能对比实验,最终确定润滑最佳油量.实验环境分为真空和大气两种.实验设定旋转半径20 mm,每次实验先在球-盘接触圆轨迹上添加定量微量润滑油,并用转速1 r/min,载荷2 N的低速轻载条件跑合10 min,保证润滑油分布均匀.正式实验选定载荷4 N,转速100 r/min连续运转1 100 min,真空摩擦磨损试验机实时采集摩擦系数并设定读取每5 min摩擦系数均值(cof)和摩擦系数标准差(cofSD).实验结束后用有机溶剂清洗球、盘,去除磨屑,并用VHX-1000超景深三维拍照显微镜观察球、盘摩擦磨损形貌,并记录球磨斑半径.
试验时,采用有机溶剂萃取和微量进样针添加的方法实现对润滑油的微量定量添加.
2.2 实验结果与分析
2.2.1 不同添加油量摩擦学性能对比
图3为添加不同油量时球-盘实验摩擦系数及标准差随时间变化情况,横坐标为实验时间,纵坐标分别为摩擦系数均值和摩擦系数标准偏差,由图3可以看出,添加润滑油 0.025 μL 和 0.1 μL 时,摩擦系数及摩擦系数标准差随时间波动剧烈,且添加润滑油0.025 μL 更明显,说明添加润滑油 0.025 μL和0.1 μL时,球-盘摩擦副间没有形成完整润滑油膜,润滑为乏油润滑.添加润滑油0.3 μL、0.5 μL、1 μL、2 μL摩擦系数和摩擦系数标准差随时间变化相对稳定,真空环境和大气环境无明显差异.
由摩擦磨损试验机记录的数据可得实验时间内摩擦系数均值,由显微镜可测量球磨斑半径,在真空和大气环境摩擦系数均值和球磨斑半径随添加油量的变化如图4所示.图4可直观看出在添加油量0.025 μL和 0.1 μL 球磨斑半径明显偏大,摩擦系数均值明显较高,说明添加油量在0.1 μL以下润滑油不足,润滑处于乏油润滑.添加润滑油0.3 μL开始,摩擦学性能得到改善,但并不是添加油量越多越好,从图上可以看到添加油量的增多并没有使磨斑半径和摩擦系数降低,反而润滑油的增多会造成搅油导致摩擦力矩增大.
2.2.2 润滑最佳油量
在载荷4 N,转速100 r/min,旋转半径20 mm的工况下,通过对不同添加油量球-盘摩擦副摩擦学性能对比,验证了此工况球-盘摩擦副润滑最佳添加油量在0.1 μL 到 0.3 μL 之间.另一方面,由于润滑油在材料表面的润湿、毛细迁移,以及滚珠滚压使润滑油流向接触区两侧等,添加的润滑油并不都能参与润滑.图5显示由于以上原因润滑油不均匀分布于接触区及其两侧,真实参与润滑的油量和添加润滑油量可按如下关系计算:
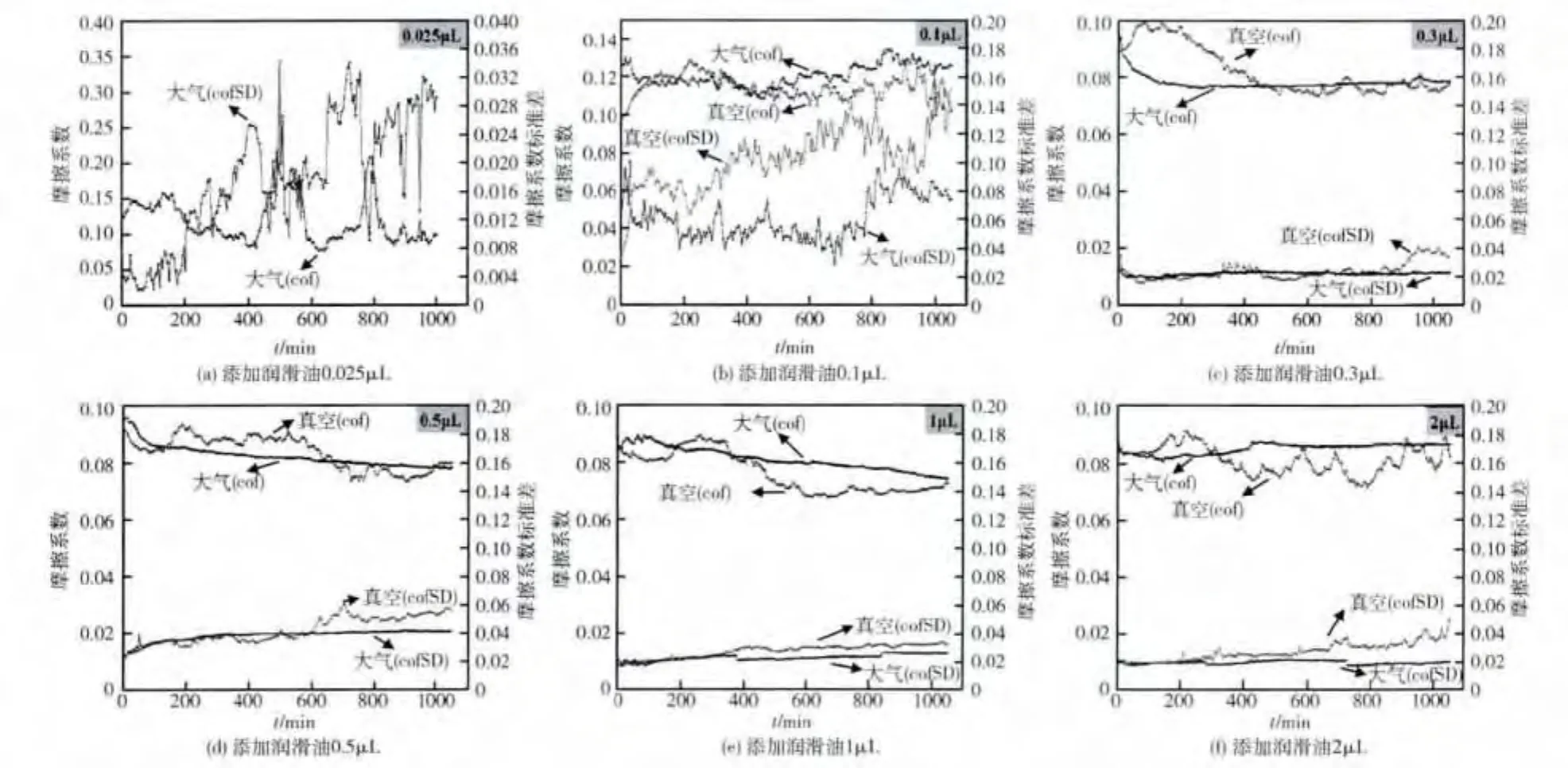
图3 不同添加油量摩擦系数及标准差随时间变化Fig.3 Variation of friction coefficient and its standard deviation with time under different adding oil quantity

图4 摩擦性能随添加油量的变化Fig.4 Variation of tribological behavior with adding oil quantity

式中,α为换算系数,D为接触区宽度;ρ为润滑油密度;L为盘上润滑油宽度;h0为接触区中心油膜厚度;h'为接触区外围油层厚度.

图5 润滑油量和添加油量的关系Fig.5 Relationship between lubricating oil and adding oil
D为润滑油弯液面起始点位置到接触中心的距离两倍,D≈4a,实验结束后测得D与此相符.L在实验结束后测定,不同添加油量不同环境L值不同.
此工况下球-盘摩擦副润滑最佳添加油量为0.1 ~0.3 μL,由式(12)实验验证的润滑最佳油量为 5.95 ~15.52 μg.
若采用前面理论分析方法同样考虑四部分油量分析此工况下球盘点接触润滑最佳油量,得到理论值为11.85 μg,理论值与实验值基本吻合,说明本文提出的估算润滑最佳油量方法的有效性.
3 算例
以某型号飞轮轴承为例,计算单个轴承润滑最佳油量.表1为该轴承结构和工作主要参数.结合赫兹接触理论,轴承运动学和动力学分析以及弹性流体动力润滑理论[4,9]校核轴承,得到轴承滚珠和沟道弹流润滑接触区尺寸和弹流润滑油膜厚度,如表2所示,由计算结果可以看出,轴承润滑接触区尺寸很小,且只需不足0.3 μm的油膜厚度足以维持轴承滚珠和沟道的润滑,因此参与轴承润滑的油量非常少.

表1 轴承结构和工作参数Tab.1 Parameters of flywheel bearing

表2 轴承校核Tab.2 Flywheel bearing Checking
按前述润滑最佳油量的理论分析方法逐步分析计算4部分油量得到单个轴承的润滑最佳油量.
(1)弹流润滑膜油量
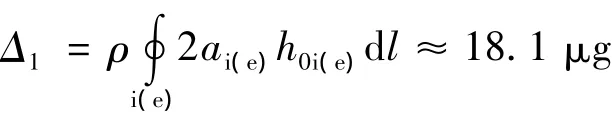
(2)润滑油弯液面油量
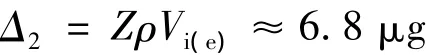
(3)表面形貌影响的油量

(4)接触入口区油量

因此单个某型号轴承润滑最佳油量为

4 结论
长寿命微量油润滑技术是卫星姿控飞轮轴承关键技术之一,润滑油过多和过少都将导致飞轮轴承摩擦力矩增大及其寿命的降低,因此轴承存在润滑油适量范围,即轴承润滑最佳油量.本文主要结论有:1)基于弹流润滑理论,提出了一种估算飞轮轴承润滑最佳油量的理论分析方法.通过开展了球-盘摩擦副实验,比较不同添加油量球-盘摩擦副摩擦学性能,验证了提出的润滑最佳油量理论分析方法的有效性.2)以某型号飞轮轴承为算例,润滑单个轴承的最佳油量约为59.8 μg.3)大气环境和真空环境的轴承润滑最佳油量无明显差异.
[1]屠善澄.卫星姿态动力学与控制(4)[M].北京:宇航出版社,2006:225-226.
[2]周宁宁,卿涛,周刚.飞轮用轴承组件摩擦力矩特性研究[J].空间控制技术与应用,2013,39(3):54-58.ZHOU N N,QING T,ZHOU G.On the friction torque properties of bearing assemblies in fly wheel[J].Aerospace Control and Application,2013,39(3):54-58.
[3]刘泽九,贺士荃,刘晖.滚动轴承应用手册[M].北京:机械工业出版社,2006:308-322.
[4]温诗铸,黄平.摩擦学原理[M].北京:清华大学出版社,2008:68-70.
[5]WEDEVEN L D,EVANS D,CAMERON A C.Optical analysis of ball bearing starvation[J].ASME Journal of Lubrication Technology,1971,93:349-363.
[6]HAMROCK D.Isothemal elastohydrodynamic lubrication of point contacts,Part IV——starvation results[J].ASME Journal of Lubrication Technology,1977,99:15-23.
[7]杨沛然,崔金磊,兼田桢宏,等.线接触弹性流体动力润滑的供油条件分析[J].摩擦学学报,2006,26(3):242-246.YANG P R,CUI J L,KANETA M,et al.Analysis of oil-Supply conditions for elastohydrodynamic lubrication in line contacts[J].Tribology,2006,26(3):242-246.
[8]尹昌磊,杨沛然.椭圆接触弹性流体动力润滑的供油条件分析[J].摩擦学学报,2007,27(2):147-151.YIN C L,YANG P R.Analysis of oil supply conditions for EHL in elliptical contacts[J].Tribology,2007,27(2):147-151.
[9]HARRIS T A,KOTZALAS M N.滚动轴承分析[M].罗继伟,马伟,译.北京:机械工业出版社,2009:29-184.
