基于迹向控制量的编队星群相位控制

吴会英，周美江，齐金玲

(上海微小卫星工程中心，上海201203)

0 引言

编队飞行技术自20世纪90年代后期发展以来已有一些应用实例，如NASA的“陆地行星探测者计划”为4颗跟踪卫星绕1颗参考卫星的编队构型，用于验证光谱分析和编队飞行干涉成像等多项关键技术.

编队飞行技术虽然有着重大的应用前景，但仍处于起步阶段，一些关键技术的突破已成为卫星编队具体实现的重要因素.由于编队卫星功能的实现依赖于编队构型，所以构型设计、构型重构和构型保持已成为编队卫星发展的关键技术.尤其对于50 kg以下的微小卫星，资源严重受限，进行编队飞行有着更加严苛的工程约束.如何在这些工程约束下开展复杂航天任务，掌握构型形成与保持的控制方法是亟待攻克的关键技术之一.

已有诸多学者基于Hill方程［1］对两星的编队飞行轨道控制策略进行了深入分析［2-4］，基于绝对轨道的编队星群轨道控制策略也不乏研究文献［5］，但二者对编队构型中最为基本的星群相位控制问题涉及甚少.

对于共面编队问题来讲，卫星在轨道面内的相对运动为长半轴是短半轴两倍的迹向漂移椭圆，编队构型的保持即相对运动椭圆几何特性的保持，包括椭圆大小的保持和星群在椭圆上相对相位的保持.

通过2008年SZ-7伴星在轨伴飞任务的成功执行，对设计的伴飞轨道控制策略进行了基于真实轨道数据的验证［6］，得到了共面绕飞问题中在相对运动椭圆上下点进行控制对椭圆短半轴控制效率最高的结论.文献［7］延续文献［6］的研究成果，对共面绕飞问题中控制时机如何改变相对运动椭圆大小问题作了深入研究，推导了控制时机对相对运动椭圆大小改变的解析解.但遗憾的是，文献［6］与文献［7］仅针对相对运动椭圆大小控制改变问题进行了研究，对多星集群编队问题中十分关键的星群相对相位控制并没有涉及，而且由于小卫星资源匮乏，实时的轨道控制基本不可能实现，亟待开展基于实际工程约束的编队星群相位控制与保持技术研究.

本文立足于工程应用，考虑编队小卫星平台姿控能力较弱，或出于任务的特殊性仅能进行迹向控制，基于Hill方程开展编队星群相对相位控制问题研究，通过求解控制时机对相对相位改变的解析解，使复杂的相位控制问题可以通过分析其相对简单的解析解开展研究.

1 共面绕飞编队星群相位控制

1.1 相对运动方程解

共面绕飞两航天器在轨道面内的相对运动解为相对轨道坐标系(x轴径向朝天，由地心指向参考航天器，y轴在轨道面内垂直于x轴沿飞行方向，z轴符合右手定则)中长半轴为短半轴两倍的迹向漂移椭圆［1］

式中，b为椭圆短半轴，(xc，yc)为椭圆中心，xc=xc0，yc=yc0-1.5xc0nt，n为航天器平均运动角速度，xc0、yc0为初始时刻的椭圆中心，t为自初始时刻起算的时间.根据Hill方程可知

相对运动参数解为

nt+θ为卫星在相对运动椭圆上的相位，定义见式(4)，θ为初始相位，由初始时刻的相对运动参数决定.

1.2 编队卫星相位

根据式(3)，卫星在相对运动椭圆上的相位定义为

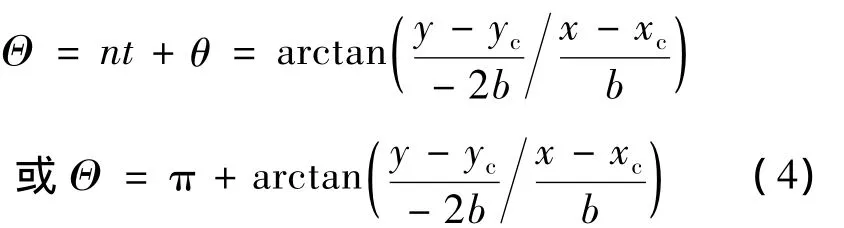
需要说明的是，式中Θ具体取哪一个值由sinΘ=(y-yc)/(-2b)，cosΘ=(x-xc)/b的符号共同决定.

由式(4)可知，卫星在相对运动椭圆上的相位Θ是由相对运动椭圆的内切圆和外接圆辅助定义的，从正x轴起算，逆时针旋转为正.

以相位相差90°两卫星绕主星的伴随飞行为例说明相位的定义，如图1示，初始相位为0°的A星与初始相位为90°的B星，经过t时间后，A星运动到相位为ΘA的A'处，B星运动到相位为ΘB的B'处，依然有ΘB-ΘA=90°，相位角的增加方向为相对运动方向.

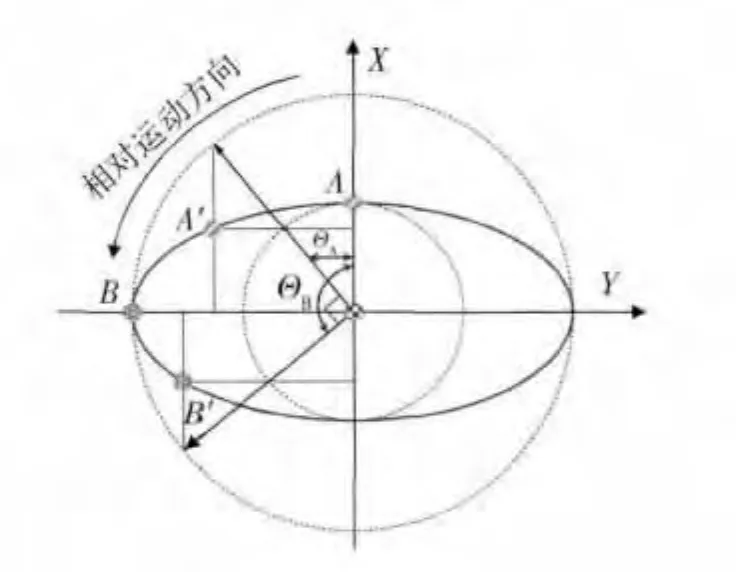
图1 相位示意图Fig.1 Phase sketch

1.3 编队卫星相位控制

首先，控制时机为控制的时刻，本节首先介绍相位控制过程中控制时机与相位改变的关系.

编队卫星在执行任务过程中需要保持稳定的构型，其中之一就是保持星群间的相对相位稳定.由式(4)可知，控制量对相位的改变是通过改变椭圆中心位置xc、yc和椭圆短半轴b实现的.本文以卫星只能进行迹向控制为例进行相位控制问题研究，由式(2)可知，迹向控制量ΔV会改变椭圆中心径向坐标xc和椭圆短半轴b的大小，对于cosΘ=(xxc)/b，其大小和符号都可能发生改变;但对于sinΘ=(y-yc)/(-2b)，虽然ΔV改变椭圆中心径向坐标xc(由yc=yc0-1.5xc0nt易知即改变了椭圆中心漂移速度)，但漂移量yc=yc0-1.5xcnt是一个随时间累积的量，速度增量作用瞬时不会突变，所以sinΘ只可能改变大小，但符号不变，即控制前后相位在同一x半平面.控制时机与相位改变量满足如下关系:

若ΔΘ∈(-π，0)，则可选控制时机为Θ∈(2kπ-ΔΘ，2kπ+π)∪ (2kπ-π-ΔΘ，2kπ);

若ΔΘ∈(0，+π)，则可选控制时机为Θ∈(2kπ，2kπ+π-ΔΘ)∪ (2kπ-π，2kπ-ΔΘ).

其次，控制量为控制的脉冲速度增量大小，下文介绍相位控制过程中控制量与相位改变的关系.

设迹向控制量ΔV引起的相位改变量为ΔΘ，由式(2)、(3)和(4)得到控制前后相位角为

式(5)中两式相除，可得控制量ΔV引起的相位改变量ΔΘ为

将式(6)变形可得要改变ΔΘ的相位角所需的控制量ΔV为

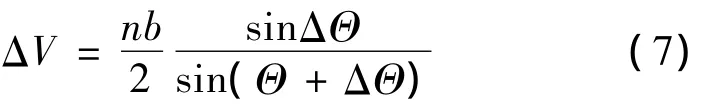
最后，控制量与控制时机构成了控制的全部要素，下文将讨论3种特殊的控制时机，并给出3种控制时机对应的控制量.

由式(7)可知，对于一定的相位改变量ΔΘ，所需控制量ΔV与控制时机Θ相关，可以通过选择最优控制时机Θ*使控制量ΔV最小.由式(7)可知当sin(Θ+ΔΘ)=±1时，所需控制量绝对值最小:ΔVmin=sinΔΘ(nb/2)，对应的最优控制时机为Θ*=kπ+π/2-ΔΘ(k为整数，下文同)，为最省燃料的相位控制，这种控制模式对资源受限的编队小卫星意义重大.

由前面的分析可知，控制前后相位在同一x半平面，对于最省燃料的控制即有:

1)若 sin(Θ*+ΔΘ)=1，即控后相位 Θ*+ΔΘ=2kπ +π/2∈(2kπ，2kπ +π)，则控前相位应有:Θ*=2kπ +π/2-ΔΘ∈(2kπ，2kπ +π)，可得相位改变量-π/2＜ΔΘ＜π/2;

2)若 sin(Θ*+ΔΘ)=-1，即控后相位 Θ*+ΔΘ=2kπ -π/2∈(2kπ -π，2kπ)，则控前相位应有:Θ*=2kπ -π/2-ΔΘ∈(2kπ -π，2kπ)，可得相位改变量-π/2＜ΔΘ＜π/2.即只有需要改变的相位角ΔΘ∈(-π/2，π/2)为锐角时，才能找到最省燃料的控制时机.此时若最小控制量 ΔVmin=sinΔΘ(nb/2)，则最省燃料的控制时机为Θ*=2kπ+π/2-ΔΘ;若最小控制量为ΔVmin=-sinΔΘ(nb/2)，则最省燃料的控制时机为Θ*=2kπ-π/2-ΔΘ.

由式(7)还可知，一定相位改变量ΔΘ对应的控制量ΔV还与椭圆短半轴b相关，短半轴b越大，所需控制量ΔV也越大.所以编队构型尺度大的卫星在进行相位调整时，燃料耗费相对也多.但对于最省燃料的控制，根据文献［7］的推导，最省燃料控制时椭圆短半轴将改变:

即无论是控大还是控小相位，最省燃料控制总是会朝着将椭圆短半轴减小的方向进行.椭圆短半轴减小，后续进行最省燃料相位控制所需的控制量也会减小.

1.3.2 不改变相位的控制时机

编队星群的相位控制到位后，希望后续控制不改变当前相位.由式(4)可知，迹向控制量ΔV一定会改变椭圆中心径向坐标xc，从而改变 cosΘ=(x-xc)/b的值;但可以选择sinΘ≡0，Θ=kπ(相对运动椭圆上下点)的时机进行控制，则控制前后相位均为0，控制不改变相位.

据有关数据显示，中国矮小症发病率约为3%，现有矮小人口约3900万人。然而，每年真正接受治疗的患者不到3万人。70%以上的家长对矮小症缺乏足够的了解，不认为矮小是一种病，以致错过了孩子的最佳治疗期，严重影响了孩子的生长发育。

虽然理论上讲，在相对运动椭圆上下点进行控制不改变相位，但实际在轨时，由于测定轨误差，上下点可能会找不准，y-yc≠0为一小量;若此时恰好需要施加的控制量较大，且|ΔV|→nb/2为减小椭圆趋势，可能会使|x-xc|→ 0，此时的括号为0:0型未定式，相位改变不可预期，为数学奇点.图2和图3为在不同控制时机施加同一控制量对相位的改变情况.

图2 正控制量引起的相位改变与控制时机的关系Fig.2 Relation of phase change and the time of control with positive ΔV

由图2和图3可知:

1)当控制量|ΔV|＜nb/2时，在上下点进行控制不改变相位，相位改变极值点出现在与控制时机对应相位相加和为±90°的地方;

2)当控制量|ΔV|＞nb/2时，在上下点进行控制，可能会使椭圆先减小至零后增大，上下点对调，相位改变180°，故在工程应用时对于小尺度的编队构型，应尽量避免较大的速度增量，具体的速度增量上限值需要根据构型尺度以及工程经验来确定.

图3 负控制量引起的相位改变与控制时机的关系Fig.3 Relation of phase change and the time of control under negative ΔV

1.3.3 趋近最小控制量的控制时机

当需要改变的相位角ΔΘ∈［π/2，π］∪［-π，-π/2］时，在可选控制时机区间内找不到最省燃料控制的控制时机，此时可分次进行最省燃料控制，也可以在可选控制时机内任一控制时机进行控制，所需控制量按式(7)计算.由式(7)可知，在可选控制时机内对不同时机进行控制，控制量大小不同，选择的时机进行控制，此时控制量趋近最小控制量:

需要注意的是:控制时机无限趋近kπ，但不等于kπ，因为1.3.2分析表明在相对运动椭圆上下点(Θ=kπ)进行控制不改变相位.所以实际应用时，需要根据实际情况设定“无限趋近”的量化标准，使非锐角相位改变量的控制趋近最小控制量控制，尽可能节省燃料.

1.3.4 小 结

根据上文推导，可得如下结论:

1)控制量对相位的改变不是任意的，控制前后的相位在同一x半平面.即若ΔΘ∈(-π，0)，则可选控制时机为Θ∈(2kπ-ΔΘ，2kπ+π)∪(2kππ -ΔΘ，2kπ);若 ΔΘ ∈ (0，+π)，则可选控制时机为Θ∈(2kπ，2kπ +π-ΔΘ)∪(2kπ -π，2kπ -ΔΘ).

2)若需要改变的相位角ΔΘ∈(-π/2，π/2)为锐角，可在Θ*=2kπ+π/2-ΔΘ处施加ΔVmin=sinΔΘ·(nb/2)或在Θ*=2kπ-π/2-ΔΘ处施加ΔVmin=-sinΔΘ·(nb/2)的控制量进行最省燃料控制，最省燃料的相位控制总是会将相对运动椭圆控小;

3)在相对运动椭圆上下点进行控制不改变相位，但对于小尺度构型，上下点不易准确得到，可能导致相位发生不可预期的改变;

4)若需要改变的相位角ΔΘ∈［π/2，π］∪［-π，-π/2］，找不到最省燃料控制的控制时机，但可在可选控制时机内选择Θ→kπ的时机进行控制，此时控制量趋近最小控制量ΔVmin=±nb/2.

2 仿真算例

2.1 仿真输入

为验证本文理论的正确性，引入仿真实例进行验证.其中主星为 700 km高度，交点周期为5 920.374 s，初始绕飞椭圆短半轴平均值为3.781 km，|nb/2|≈2 m/s，副星绕主星共面绕飞，对副星施加控制.约定用本文公式计算得到的相位改变量为“理论值”，考虑高精度的HPOP数值外推，并考虑所有摄动，STK仿真得到的相位改变量为“仿真值”，比较“理论值”和“仿真值”的符合程度，即可验证本文理论的正确性.

2.2 仿真结果

表1中的“控前相位”即为用相位角表示的控制时机，仿真结果如表1所示.

由表1得到结论如下:

1)对需要改变的相位角为 +19.993°和 -19.989°的情况进行了最省燃料控制仿真，相位改变量的理论值和仿真值相符，验证了最省燃料控制理论的正确性;

2)在相对运动椭圆上下点(0°和180°)施加控制，当实施的控制量小于nb/2时，相位改变量的仿真值为0，与理论值相同;

3)在相对运动椭圆上点(0°)附近施加控制，当实施的控制量大于nb/2时，椭圆短半轴几乎减小为0，相位改变较大，表1中的仿真值与理论值的差异是计算过程中的舍入误差造成的.

表1 仿真效果Tab.1 Simulation results

3 结束语

本文基于卫星只能进行迹向控制的一种微小卫星在轨情况，应用Hill方程推导了控制量和控制时机对编队星群相位改变的关系，得到了当需要改变的相位角为锐角时可进行最省燃料的控制，在相对运动椭圆上下点进行控制不改变相位，当需要改变的相位角为非锐角时可进行分次控制等结论，并通过仿真验证了理论的正确性.

具体应用时，可根据本文推导的理论依据实际情况选择控制模式、规划控制量和控制时机.对于卫星可进行其他方向控制的情况，也可参照本文的推导方式进行进一步推导，结合实际工程约束进行规划.

本文旨在给出控制量、控制时机和编队卫星相位改变量之间的直观公式，在任务分析阶段可用此公式进行燃料估算和控制模式的初步规划.对编队星群来讲，进行相位控制必然会引起构型其他特征参数的改变，其耦合性使得编队星群的构型控制必须从全局综合考虑，限于篇幅，本文不再详细介绍，具体的构型控制与保持将作为下一步研究的问题.

［1］郗晓宁，王威，高玉东.近地航天器轨道基础［M］.长沙:国防科技大学出版社，2003:244-247.XI X N，WANG W，GAO Y D.Fundamentals of nearearth spacecraft orbit［M］.Changsha:Nation University of Defense Technology Press，2003:244-247.

［2］文援兰，宋以胜，文景.共面编队飞行卫星星座的控制［J］.国防科技大学学报，2004，26(3):24-28.WEN Y L，SONG Y S，WEN J.The control of the satellites coplanar formation flying［J］.Journal of National University of Defense Technology，2004，26(3):24-28.

［3］黄美丽，向开恒.编队飞行卫星群相对轨道摄动运动分析［J］.中国空间科学技术，2006，26(6):13-19.HUANG M L，XIANG K H.Perturbation analysis of the relative orbits of formation flying satellite［J］.Chinese Space Science and Technology，2006，26(6):13-19.

［4］师鹏，李保军，赵育善.有限推力下的航天器绕飞轨道保持与控制［J］.北京航空航天大学学报，2007，33(7):757-760.SHI P，LI B J，ZHAO Y S.Orbital maintenance and control of spacecraft fly-around with finite-thrust［J］.Journal of Beijing University of Aeronautics and Astronautics，2007，33(7):757-760.

［5］杨维廉.基于轨道摄动解的卫星编队飞行［J］.宇航学报，2008，29(4):1166-1171.YANG W L.Formation flying based on orbit perturbation solution ［J］.Journal of Astronautics，2008，29(4):1166-1171.

［6］吴会英，陈宏宇，余勇，等.远距离轨道接近及绕飞控制技术研究［J］.中国空间科学技术，2010，30(1):25-33.WU H Y，CHEN H Y，YU Y，et al.Study of long-distance approaching and companion flying technology［J］.Chinese Space Science and Technology，2010，30(1):25-33.

［7］吴会英，陈宏宇，周美江，等.伴随卫星轨控时机与相对运动椭圆大小控制效率的关系［J］.载人航天，2013，19(5):90-96.WU H Y，CHEN H Y，ZHOU M J，et al.Research on relation between orbit control time and control efficiency of company satellites［J］.Manned Spaceflight，2013，19(5):90-96.