古塔变形量的分析与研究

刘之林，李兴莉

（重庆房地产职业学院，重庆401331）

1 问题的提出与模型假设

1.1 问题提出

以国内某古塔为例，管理部门委托测绘公司先后于1986年7月、1996年8月、2009年3月和2011年3月对该塔进行了4次观测。根据观测数据提出了以下问题：

（1）给出确定古塔各层中心位置的通用方法，并列表给出各次测量的古塔各层中心坐标。

（2）分析该塔倾斜、弯曲、扭曲等变形情况。

（3）分析该塔变形的趋势（有关数据参见2013年全国大学生数学建模竞赛C题）。

1.2 模型假设

（1）假设古塔各层质量分布是均匀的。

（2）假设每年自然环境因素对古塔变形的影响基本相同。

（3）假设题中所给测量数据准确无误。

（4）假设每次测量时各测量点的位置不变。

2 模型的建立与求解

2.1 缺失数据的处理

由于在1986年和1996年的测量数据中缺少第十三层第五号测量点的数据，为了能够用一个通用算法求出各年第一层至第十三层各层的中心点坐标，本研究利用SPSS软件分别对第一层至第十二层的第五号测量点的横坐标、纵坐标、竖坐标分别进行拟合，并预测出第十三层第五号测量点的测量数据。

首先，利用SPSS软件所提供的十一种模型对所给数据进行初步分析，发现对于横坐标和纵坐标，二次模型效果最好；对于竖坐标，立方模型效果最好。以1986年数据为例：拟合优度（调整R方） 分别为 0.979，0.995，1.000， 显著性检验值（Sig．）均为 0。经过计算，1986 年和 1996 年第十三层第五号测量点的坐标预测值分别为（567.986,519.737,53.012）,(567.992,519.73,53.014)

2.2 计算各层中心点的坐标

2.2.1 模型建立

由于存在变形因素的影响，古塔各层的中心点产生了微小的变化，每层的中心点到该层各测量点的距离只能近似相等，即中心点到各测量点的距离两两差值的绝对值之和应该接近于零。显然，此和式的值越小，中心点的位置就越精确。所以，古塔各层楼面上得到所有测量点的距离两两差值的绝对值之和最小的点即为该层楼面的中心点。

设第 k 层（k=1，2，…，13）的中心点的坐标为（x(k)，y(k),z（k）），第 k 层第 i个（i=1,2,…，8）测量点的坐标为(x(k，i),y(k,i),z(k,i))，d(k,i)为第 k 层中心点到该层第 i个测量点距离；mx(k)、my(k)、mz(k)分别为第k层各测量点横坐标、纵坐标、竖坐标的最小值，Mx(k)、My(k)、Mz(k)分别为第 k 层各测量点横坐标、纵坐标、竖坐标的最大值。

我们以第k层中心点的三个坐标值x(k)、y(k)、z(k)为决策变量，以第k层中心点到各测量点的距离两两差值之和最小为目标函数，以x(k)、y(k)、z(k)分别界于第k层各测量点的横坐标、纵坐标、竖坐标的最小值与最大值之间为约束条件，建立非线性规划模型：

2.2.2 模型求解

根据所给数据利用MATLAB编程计算，可以获得1986年、1996年、2009年、2011年古塔各层的中心位置的坐标。其中1986年各层中心点的坐标如表1所示。

2.2.3 误差分析

由于古塔变形，中心点到各测量点的距离不尽相等，模型的计算也有可能存在偏差。本研究以每层中心点到各测量点的距离两两差值的平均值作为计算该层中心点的系统误差，再计算出各层系统误差的平均值，并以此平均值作为计算古塔中心点坐标的平均误差。

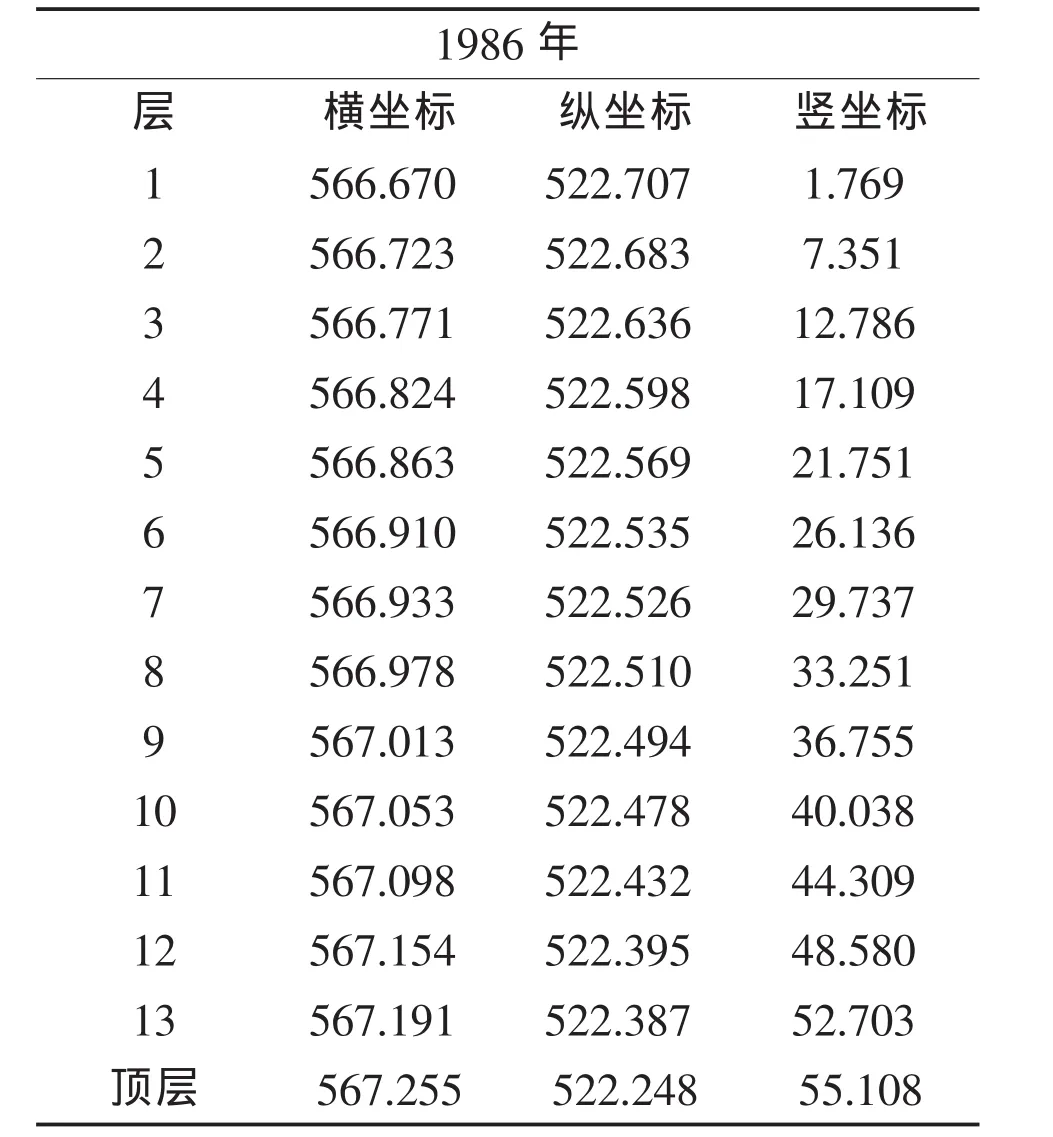
表1 1986年古塔各层中心坐标

设εk为计算第k层中心点坐标的系统误差，ε为各层系统误差的平均值，则

利用Matlab计算结果如表2所示：

表2 计算中心点坐标的平均系统误差(单位：m)

2.3 计算各层倾斜变形量

古塔各层的测量点在地平面上的投影为一个八边形（如图1），设第一层中心点为O1，过O1作第一层所在平面的垂线

图1 古塔各层测量点在地平面的投影

O1P（初始中轴线），第k层的中心点为Ok，Ok在第一层所在平面上的投影点为O'k，Ok在O1P上的投影为O''k，Ok到O''k的距离dk即为第k层中心点的倾斜位移，O1Ok与O1P的夹角θk即为第k层相对于初始中轴线的倾斜角度。

设 Ok的坐标为（x(k),y(k),z(k)），O1的坐标为（x(1),y(1),z(1)），于是 O''k的坐标为（x(1),y(1),z(k)）， lk为Ok到O1的距离，hk为O''k到O1的距离，则

根据解析几何知识，在ΔO'1OkO''k中有：

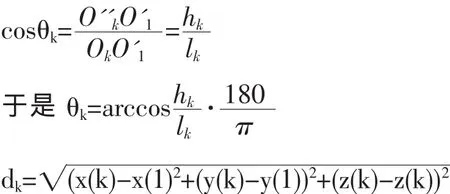
利用Matlab计算，可求得各层中心点相对于初始中轴线的倾斜角度θk与倾斜位移dk，结果如表3所示。

表3 各层倾斜角度与倾斜位移

出于对建筑物安全系数的考虑，θk选取最大值，在现实生活中，对一栋建筑物选取最大的倾斜角度，有助于提醒工作人员及时维修或采取其他措施以达到保障建筑物安全的目的。在这里选取 θk（k=1,2,…，13）的最大值作为此古塔的倾斜角。古塔各层最大倾斜角度与倾斜位移如表4。

表4 古塔各层最大倾斜角度与倾斜位移

以上结果表明，从第二层到十三层，各层的倾斜角度、倾斜位移都有呈逐年增加的趋势。最大倾斜角度的年均增长量为0.01187度，最大倾斜位移的年均增长量为0.01615m。

2.4 计算各层的扭曲变形量

古塔的扭曲度是指古塔各层的测量点相对于底层各对应测量点存在一个水平旋转角度。假设第k层中心点在第一层所在平面上的投影为O'k（k=1,2,…13），第一层各测量点记为 Nki（k=1,2,…,13,i=1,2,…,nk）。如果古塔没有发生扭曲变换，那么OK、Nki两点的连线在第一层所在平面上的投影O'kN'ki应该与O1N1i重合，但是由于存在扭曲变形，它们之间是不重合的，其夹角即为第k层第i个测量点的扭曲度。

设αki为第k层第i个测量点相对于第一层第i个测量点的扭曲角度（如图2），根据平面知识，可知

图2 第K层与第一层测量点的扭曲角

其中 kli、kki分别为 O1N1i与 O'kN'ki的斜率。

我们定义每层8个测量点相应扭曲度的最大值为该层的扭曲度，第一层至第十三层各层扭曲度的平均值为古塔的扭曲度，利用Matlab计算，各年的平均扭曲度分别为：3.8023771，3.8158038，3.0679394，3.0683079。

2.5 计算古塔的弯曲变形量

由于存在扭曲变形，古塔各层中心点不在同一平面。为了便于研究古塔的弯曲程度，我们对各层中心点进行坐标变换：先将坐标原点平移至第一层中心点处，然后将各层中心点绕轴旋转至坐标平面x'o'z内（如图3），变换公式为：

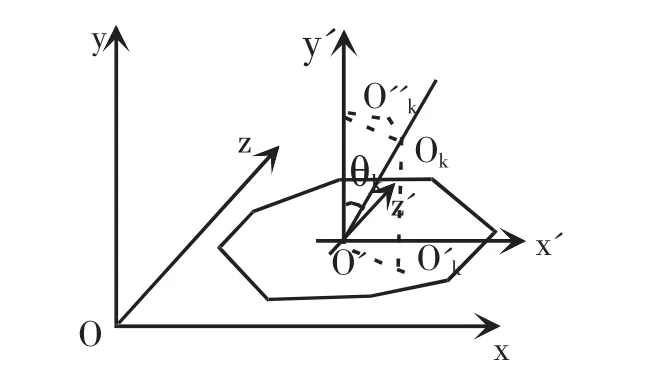
图3 坐标变换图

其中（x01,y01,z01）为第一层中心点坐标。经过平移变换和旋转变换以后的各层中心点坐标如表5所示（以1986年和1996年数据为例）。

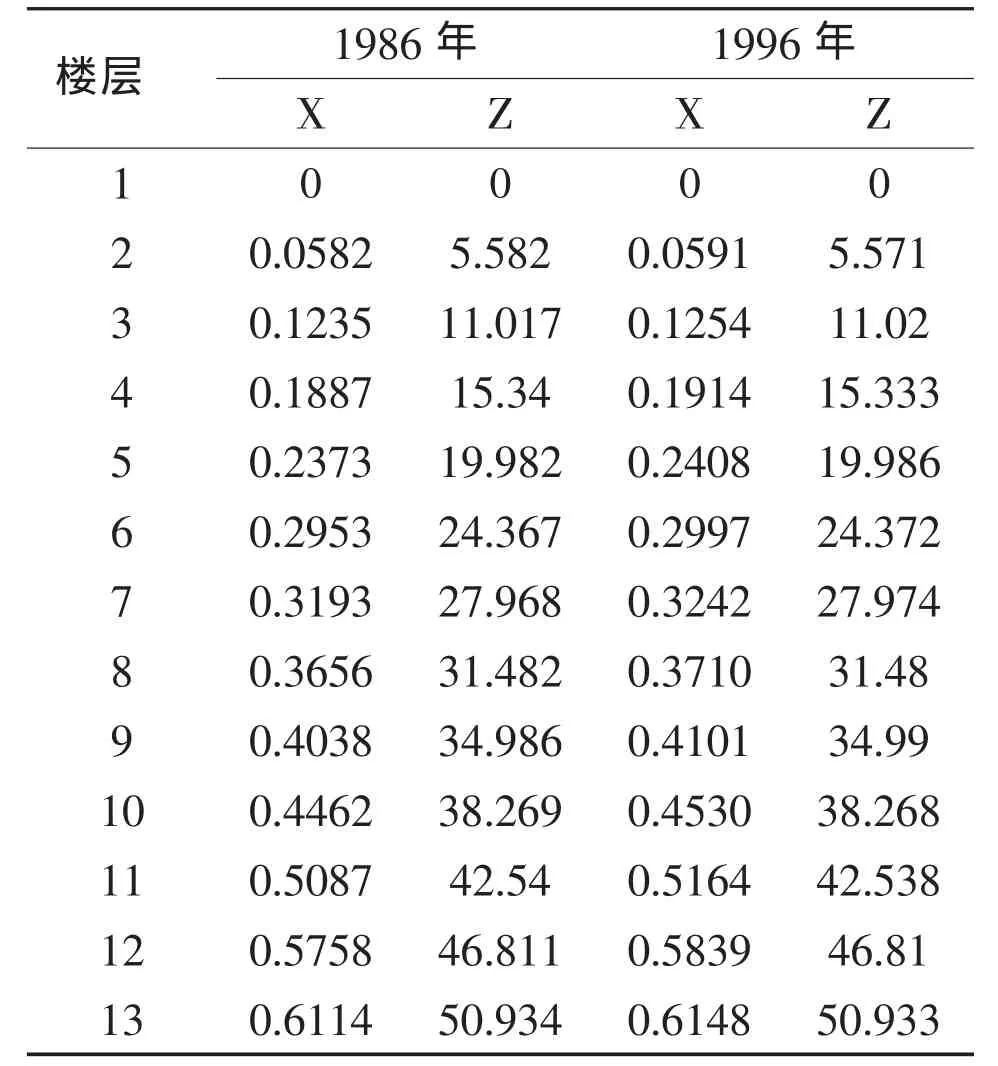
表5 变换以后的各层中心点坐标

经过以上坐标平移和旋转变换以后，各层中心点均旋转至xoz平面上，为了计算古塔的弯曲程度，我们利用Matlab对其进行曲线拟合。根据各层中心点散点图的特点，可选用二次函数来进行拟合，拟合结果如表6。

表6 各层中心点所在曲线的拟合参数值

根据解析几何的知识，曲线的弯曲度可用曲率来表示，计算公式为

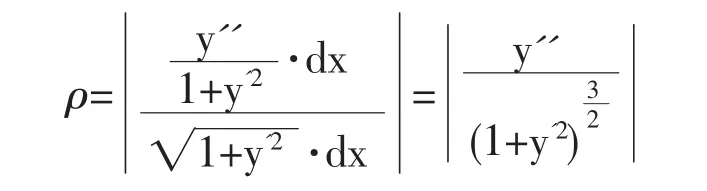
根据拟合得到的函数，利用Matlab计算求得1986年、1996年、2009年、2011年的平均曲率分别为：0.00003474995，0.00002862823，0.00037136045，0.00036879992。

2.6 古塔的变形趋势分析与预测

2.6.1 模型建立

在分析古塔的变形趋势时，由于原始数据序列中只有四个数据，且时间间隔不等，用任何常规的模型都很难得到较高的拟合优度。为了更好地分析、预测古塔未来的变化趋势，我们采用非等距灰色GM（1,1）模型进行分析和预测。

第一步，数据检验与处理。

对原始数据序列进行检验和预处理以保证所建模型的可行性以及预测的准确性。设原始数据序列为:

X(0)={x(0)(k1),x(0)(k2),…,x(0)(kn)}，时间间距为

Δki=ki-ki-1(i=2,3,…,n)。

计算原始数据序列的级比

第二步，建立非等距的GM(1,1)模型 。

将数据序列X(0)一次带权累加生成数列X(1)={x(1)(k1),x(1)(k2),…,x(1)(kn)}，其中1,2,3…n（其中 Δk1=1）

计算均值数列：

z(1)(ki)=0.5x(1)(ki)+0.5x(1)(ki-1)(i=2,3,…,n)。

然后，由一次累加生成序列X(1)建立灰模型GM（1,1），灰微分方程为：

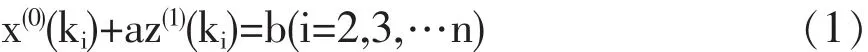
白化微分方程为：

其中a（发展系数）与b（灰作用量）为待辨识参数。利用最小二乘法可以求得：

[a,b]=(BTB)-1BTY

其中

于是（2）式的解即时间响应方程为：

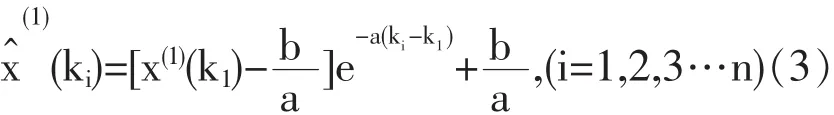
再做累减生成，可得到模型的还原值，公式如下：

第三步，检验预测值。

（1）残差检验：令 ε(k)为残差

一般要求 ε(k)＜0.2,如果 ε(k)＜0.1 就比较好。

（2）级比偏差检验：令ρ(k)为级比偏差

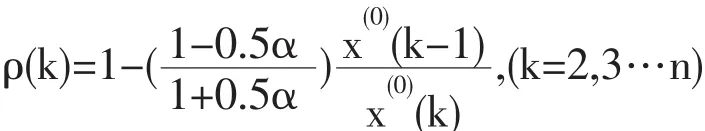
一般要求 ρ(k)＜0.2,如果 ρ(k)＜0.1 就比较好。

2.6.2 用灰预测对倾斜角度的分析、预测

第一步：对原始数据列。

X(0)=0.79868455,0.79876666,0.82121955,0.82326289

计算级比，得到

λ=(0.9998972015,0.9726590910,0.99755179957),经验证级比级数据均落在可容覆盖

(0.6703200460,1.3956124251)内，说明原始数据序列适合灰模型。

第二步：将原始数据序列进行加权累加得到。X(1)=（0.79868455，8.78635117，19.46220533，21.10873112）

通过Matlab编程求解，a=-0.0016479784，b=0.7928815402，倾斜角的时间响应方程为：

还原模拟式为：

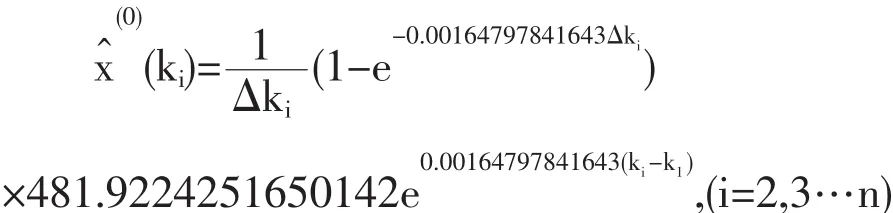
经计算得到预测还原值：

第三步：残差检验。将原始数据序列与预测还原值分别代入上式中计算出残差与级比偏差，结果如下表7。

表7 倾斜角分析

从上表可以看出预测的结果和原始数据非常吻合，所以采取灰预测是一个有效合理的预测方法。

第四步：预测最大倾斜角度的变化趋势。古塔变形的年均变化量是很小，因此如果预测的时间太短就缺乏实际意义。我们以原始数据序列的时间区间向外推1/3作为预测的时间点，即对2019年的最大倾斜角度进行预测。

经Matlab计算，2019年古塔的最大倾斜角度约为0.833081。

2.6.3 对倾斜位移、扭曲度、弯曲度的分析与预测

将1986年、1996年、2009年、2011年各年的最大倾斜位移、扭曲度、弯曲度分别代入上面建立的灰模型中，即可计算出相应的待辨识参数的值以及时间响应方程，并可预测出2019年的变形量，预测结果如下表8。

表8 倾斜位移、扭曲度、弯曲度的预测结果

3 结论

本研究建立的计算中心点坐标以及确定三种变形量的模型具有简单明了、处理方法巧妙，且速度快、效率高、实用性强的特点，所得结果对于古塔管理的相关部门制定必要的保护措施具有一定的指导意义。但在对古塔的变形趋势进行预测时，由于原始数据序列的数据量太少，而且2009年的数据存在异常变化，虽然我们选用了比较科学的预测方法——灰模型，但仍不可避免地存在一定的偏差。

[1]陈东佐,康玉庆.中国古塔的维修与保护[J].太原大学学报,2006(4).

[2]李文军,付世禄.浅析倾斜建筑物纠偏[J].中国地质灾害与防治学报,2000(1).

[3]张志勇,杨祖樱.MATLAB 教程：R2011a[M].北京：北京航空航天大学出版社,2011.

[4]刘圣保,张公让,李巧巧,汤义强.非等间距GM（1,1）模背景值的改进及其最优化[J].合肥工业大学学报,2010（11）：1749-1752.

[5]同济大学数学教研室.高等数学：上册,第四版[M].北京：高等教育出版社,2002.

[6]罗应婷,杨钰娟.SPSS统计分析从基础到实践：第2版[M].北京：电子工业出版社,2010.