铁路混凝土抗压疲劳设计参数研究

潘永杰，张玉玲，刘晓光，陶晓燕

(中国铁道科学研究院铁道建筑研究所，北京 100081)

混凝土梁是由不同材料组成，其发生疲劳破坏是由于梁的组成材料混凝土、非预应力钢筋和预应力钢筋发生了疲劳破坏。

对混凝土梁而言，混凝土材料主要承受压力。混凝土在加载前，内部已有许多微裂缝存在，在重复应力作用下不断吸收能量，使其内部的损伤不断增加，纵向总变形及残余变形逐渐增大，最终混凝土发生疲劳破坏，因此，在铁路混凝土桥梁设计中，应保证混凝土的抗压疲劳强度。本文主要基于《铁路桥涵设计规范(极限状态设计法送审稿)》(以下简称《送审稿》)［1］，对铁路混凝土抗压疲劳设计参数进行研究。

1 疲劳强度折减系数

混凝土轴心抗压疲劳强度系指混凝土在等幅重复应力下的疲劳强度，一般可用疲劳强度折减系数来表达。混凝土的疲劳强度常用混凝土在等幅重复应力下的疲劳强度与静载强度的比值fmax/fc予以表达，称为疲劳强度折减系数。

铁科院的姚明初、钟美秦等对混凝土在等幅和变幅重复应力作用下的力学性能试验研究表明，混凝土在等幅或变幅重复应力作用下的纵向疲劳变形增量Δε达到0.4fc的静载压缩变形时，混凝土已有严重损伤，不能有效使用［2-3］。可用下式作为混凝土在重复应力作用下的疲劳失效判据

式中:fc为混凝土轴心抗压强度;Ec为混凝土在零应力处的切线弹性模量。

根据以上分析，可推导出混凝土在等幅重复应力下疲劳失效强度与循环次数N的关系曲线

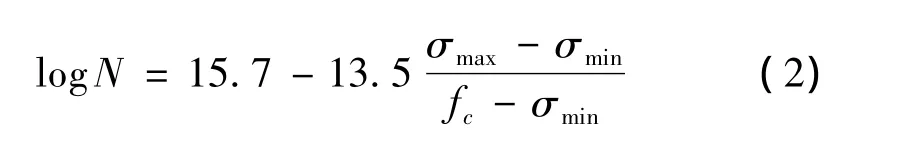
式中:σmax，σmin分别为混凝土等幅重复应力幅值的上限、下限。

当混凝土疲劳循环次数为2×106时，式(3)简化为

混凝土抗压疲劳强度设计值主要与混凝土疲劳强度的折减系数有关，因此，为了评估混凝土疲劳强度设计值的合理性，就应先确定混凝土疲劳强度折减系数的合理性。下面是两种规范对混凝土疲劳强度折减系数的规定［4］。

1)瑞典混凝土结构设计规范(BBK04)

BBK04中，混凝土受压S-N曲线采用的是Aas-Jakobsen公式，混凝土疲劳强度折减系数计算式为

式中:χ1=1/C，C为常数，取14;R为应力比，R=σmin/fmax=(σmin/fc)(fc/fmax)。

2)EC2规范

EC2规范中，混凝土受压S-N曲线与 Aas-Jakobsen公式类似，不同之处在于将(1－R)变换为，此时表达式为

式中，χ2=1/C。

据此列出混凝土疲劳强度折减系数3种表达式的计算结果，见表1。

表1 混凝土疲劳强度折减系数

结合表1中混凝土疲劳强度折减系数可知，铁科院建议值和欧洲两种规范规定值相差不大，尤其与BBK04非常接近，表明该折减系数的取值较为合理，《送审稿》中混凝土抗压疲劳强度正是基于此折减系数而来。

2 疲劳设计目标可靠指标

在疲劳检算的构造细节里，有两个基本变量，一个是疲劳荷载效应，另一个是疲劳抗力，都是用循环次数为N的等效等幅应力表示。在极限状态设计时，结构的功能函数Z应符合下式要求

式中，S为疲劳荷载效应，R为构造细节的疲劳抗力。

当随机变量R，S服从正态分布，设计目标可靠指标为βt时，抗力和作用的设计值为

式中:μR，μS分别为抗力和作用效应的均值;σR，σS分别为抗力和作用效应的标准差;αR，αS分别为抗力和作用效应的灵敏度系数，即影响权重，表达式分别为

抗力R和作用S各相关参数的对应关系见图1。

图1 抗力R和作用S各相关参数对应关系

依据灵敏度系数，当随机变量服从对数正态分布时，可得设计值FRd与可靠指标β的关系

式中:δFR为随机变量FR的变异系数。

当设计值FRd、平均值μR及δFR确定后，可反求可靠指标

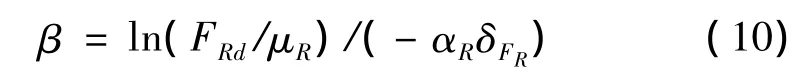
ISO 2394［5］和欧洲规范［6］对 αR，αS作了规定，见表2。

表2 抗力和作用效应灵敏度系数

可认为铁路桥梁疲劳设计的随机变量服从对数正态分布［7-8］，本文采用表2中抗力灵敏度系数的规定值0.8来反求疲劳设计目标可靠指标。

当混凝土应力下限水平σmin/fc(以下用ρ表示)取0，0.1，0.2 和0.3 时，根据《送审稿》统计结果可得混凝土轴心抗压疲劳强度平均值、变异系数和设计值。据此计算各工况下不同强度等级混凝土的疲劳设计目标可靠指标，结果见表3～表6。

将上述可靠指标计算值进行汇总，见图2。由图2可知:

1)铁路混凝土梁疲劳计算可靠指标一般＞3.5，表明混凝土疲劳设计有足够的安全储备。根据国外疲劳设计规范的相关规定［6］，疲劳目标可靠指标取3.5是合适的。

表3 不同强度等级混凝土抗压疲劳设计目标可靠指标计算值(ρ=0)

表4 不同强度等级混凝土抗压疲劳设计目标可靠指标计算值(ρ=0.1)

表5 不同强度等级混凝土抗压疲劳设计目标可靠指标计算值(ρ=0.2)

表6 不同强度等级混凝土抗压疲劳设计目标可靠指标计算值(ρ=0.3)

图2 不同强度等级混凝土的可靠指标计算值

2)随着混凝土强度等级的提高，疲劳可靠指标增大。这是因为随着混凝土等级的提高抗压疲劳强度变异系数减小。这也表明我国铁路工程结构对高强度等级混凝土的质量控制较好。

3)随着混凝土应力下限水平的提高，疲劳可靠指标增大。这是因为ρ的增加导致计算应力幅减小，相应地增加了疲劳安全度。

4)为保证混凝土与钢筋及预应力钢筋的疲劳安全度一致，本文建议铁路混凝土桥梁疲劳设计目标可靠指标取为 3.5，这与已有研究的推荐值［7-8］是一致的。

3 疲劳设计分项系数

根据可靠性设计统一标准［9］可知，材料或产品性能的设计值fd可由下式确定

式中:fk为材料或产品性能的标准值;γM为抗力(材料)分项系数。

由式(11)可知，疲劳强度的标准值和设计值确定后即可求得疲劳设计分项系数。

当疲劳设计目标可靠指标 βt为3.5时，可由式(9)求得疲劳强度设计计算值。

设计分项系数的计算步骤如下:

2)考虑运营动力系数［1］，其均值为 1.15，标准差为0.06，变异系数 δ(1+μ)=0.052 2，则总变异系数 δ为

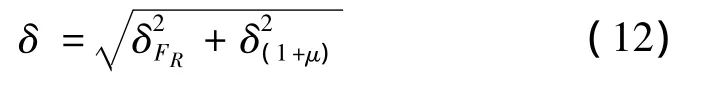
3)计算分项系数γS为疲劳强度标准值与疲劳强度设计值的比，即

4)设计分项系数γd为计算分项系数γS与运营动力系数的乘积。

疲劳强度设计值分别考虑根据设计目标可靠指标3.5反推的设计值和按规范设计取值两种情况，疲劳设计分项系数的计算结果见表7。

表7 疲劳设计分项系数γd计算结果

由表7可知，随着混凝土强度等级的提高疲劳荷载分项系数逐渐减小。这与随着混凝土等级的提高疲劳可靠指标增大的结论是一致的。

由设计目标可靠指标3.5反推的设计值和按规范取值计算得到的分项系数平均值分别为1.43和1.45，两者差别不大，可统一取为 1.45。

根据国外疲劳设计规范疲劳荷载分项系数取为1.0，此时对于抗压混凝土而言，其疲劳抗力分项系数为 1.45。

4 结论

通过对混凝土抗压疲劳设计参数的研究，得到如下结论:

1)铁路混凝土抗压疲劳设计目标可靠指标取3.5比较合理。为保证混凝土与钢筋及预应力钢筋的疲劳安全度一致，建议混凝土桥梁疲劳设计目标可靠指标取为3.5，这为确定钢筋和预应力钢筋疲劳设计参数提供了前提条件。

2)当疲劳荷载分项系数取1.0时，混凝土抗压疲劳的抗力分项系数可取1.45。

本文研究结论为修正和完善铁路混凝土抗压疲劳设计提供了依据。

［1］铁道第三勘察设计院集团有限公司.铁路桥涵设计规范(极限状态设计法)送审稿［Z］.天津:铁道第三勘察设计院集团有限公司，2011.

［2］姚明初.混凝土在等幅变幅重复应力下疲劳性能研究［R］.北京:中国铁道科学研究院，1990.

［3］钟美秦，汪加蔚.混凝土疲劳强度的研究［J］.铁道建筑，1996(9):25-29.

［4］THUN H.Assessment of Fatigue Resistance and Strength in Existing Concrete Structures［D］.Sweden:Luleå University of Technology，2006.

［5］ISO.ISO 2394 General Principles on Reliability for Structures［S］.Geneva，Switzerland:ISO，1998.

［6］European Committe for Standardization.BS EN 1990:2002 Eurocode—Basisofstructuraldesign［S］.UK:British Standards Institution，2006.

［7］潘际炎.铁路钢桥疲劳可靠度设计及铁路桥梁疲劳荷载谱研究［R］.北京:中国铁道科学研究院，1990.

［8］李铁夫.铁路桥梁可靠度设计［M］.北京:中国铁道出版社，2006.

［9］中国铁道科学研究院，中铁二院工程集团有限责任公司，铁道第三勘察设计院集团有限公司，等.铁路工程结构可靠性设计统一标准报批稿［Z］.北京:中国铁道科学研究院，2012.