列车诱发振动对转体施工桥梁稳定性影响分析

2014-05-04胡志波

铁道建筑 2014年5期

高日，胡志波，高涛，孟兮

(北京交通大学土木建筑工程学院，北京 100044)

随着我国交通事业的发展，上跨既有铁路、公路的桥梁工程日渐增多，桥梁转体施工方法越来越多地运用到城市轨道交通建设中。桥梁转体施工是指将桥梁转体结构在非设计轴线位置制作成型后，利用预设的球铰等转动设备将桥梁转动到设计轴线上的一种施工方法。它可以将在障碍上空的作业转化为岸上或近地面的作业。根据桥梁结构的转动方向，转体施工可以分为竖转法、平转法以及平转和竖转相结合的方法，其中以平转法应用最多［1-2］。

平转法施工通常应用在跨越铁路的转体桥中。这种施工方法无需在铁路线侧搭设支架，能最大限度地减少对列车正常通行产生的干扰，经济效益和社会效益十分明显。由于转体桥是在铁路线附近施工，转体梁脱架后或平衡转体过程中将会不可避免地受到列车诱发的地面振动的影响。列车通过时诱发的振动通过球铰传递到巨大的悬臂转体梁上，将会对梁体的受力产生一定影响。按照一般的处理方法，这种振动可以等效为一次有感知的地震波的输入。这种振动能否影响转体桥梁的整体安全，目前还没有文献对此进行过分析。因此，有必要开展这一方面的试验研究工作，为类似转体施工桥梁的设计、施工及运营管理积累经验和数据。

1 工程实例的选择及工程概况

秦皇岛市西部快速路工程跨越京哈铁路采用转体施工桥梁。该桥主桥为双幅独立式桥，处在直线段上，每幅桥宽23.0 m，全宽47.5 m。转体部分为2×42 m。上部结构采用预应力混凝土单箱四室箱梁。下部结构主桥转体墩采用空心矩形墩柱，下接转体平台。转体平台支撑在承台上，采用钻孔灌注桩基础。转盘结构采用环道与中心支承相结合的球铰转动体系，球铰球面半径为6.048 m。该转体桥转动角度为73.3°，每幅梁的转体质量达7 200 t。转体桥沿铁路平面布置图如图1所示。

该桥梁在转体施工前已经完成了称重和配重试验。由试验测得北侧桥梁的纵向球铰摩阻力矩为5 995 kN·m，不平衡力矩为16 650 kN·m，摩阻系数为0.015，桥梁偏向东侧，选择的配重方案为在东侧取下15 t挂板。南侧桥梁纵向球铰摩阻力矩为10 124 kN·m，不平衡力矩为8 761.8 kN·m，摩阻系数为0.025，桥梁偏向西侧。由于该侧桥梁的偏心距已满足5～15 cm的经验要求，没有进行配重。造成两侧转体摩阻力矩相差较大的主要原因是施工误差。

2 测量时程曲线

本次研究将列车诱发的地面振动等效为地震荷载。目前在工程上求解地震反应的方法分为两类:一类是拟静力法，另一类为时程分析法［3-4］。通过时程分析可以得到各质点随时间变化的位移、速度和加速度动力反应，并且可以进一步计算出结构的内力时程变化，同时时程分析法能够比较真实地、合理地模拟机构的地震响应［5］。鉴于转体桥的特点和时程分析的优点，本次研究采用时程分析法。利用加速度传感器对球铰附近地面振动情况进行测试，记录每次列车通过时的纵向、横向及竖向加速度时程曲线。表1是本次试验每组数据的列车类型和行驶方向，其中上行是指列车开往北戴河方向，下行是指列车开往南戴河方向。本次研究对15趟列车通过时转体桥球铰处的地基振动数据进行了记录。

表1 列车通过时振动测试记录

图2为地面测点平面布置图。数据采集系统的采样频率为200 Hz。

图2 地面测点平面布置

3 梁体稳定性评估

3.1 转体梁振动分析

评估列车诱发地面振动对梁体稳定性的影响时采用有限元分析法。在Midas中建立桥梁的有限元模型，采用梁单元，每幅桥共分为84个单元，85个节点，球铰简化为固定支座，模型如图3所示。

图3 转体桥有限元模型

输入每一趟列车通过时实测的加速度时程曲线，进行振动响应分析。表2～表4分别是具有代表性的客车(工况6)、动车(工况1)以及京哈两方向列车(工况9)分析结果。

表2 客车通过时转体梁振动分析结果

表3 动车通过时转体梁振动分析结果

表4 京哈两方向列车同时通过时转体梁振动分析结果

由表2～表4可知，无论是横向、纵向还是竖向，其各点最大加速度都很小，均不超过0.1g。各个方向上的最大、最小位移也很小。由此可知列车诱发的地面振动不会使梁体产生明显的振动。

3.2 球铰转动力矩分析

结构或构件倾覆的条件为倾覆力矩大于抗倾覆力矩。对本转体桥进行如图4(a)所示的简化。针对称重和配重后得到的数据，考虑最不利情况，即不平衡力矩与振动产生的转动力矩同向，此时转体桥发生倾覆的条件为

式中:MG为桥梁不平衡力矩，是球铰两侧桥梁对球铰中心产生的力矩差值;M为外部作用对转体桥产生的力矩，此处为列车振动所产生的力矩;MC为撑脚对球铰中心产生的力矩，此处假定一个撑脚与承台接触;MZ为球铰摩阻力矩。

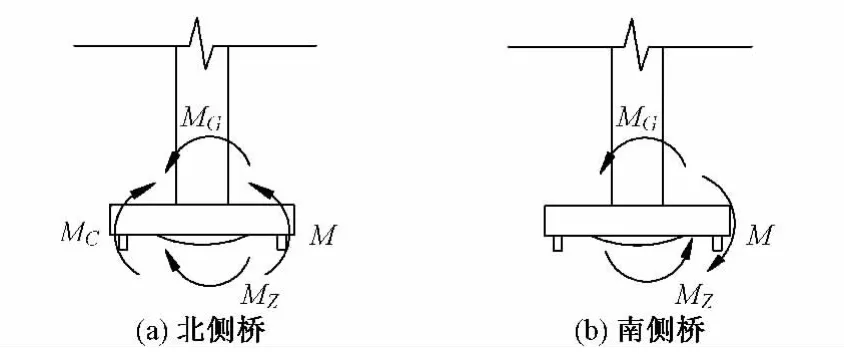
图4 转体梁受力分析

通过计算分析后可得北侧转体桥配重后桥梁的不平衡力矩为14 886 kN·m;南侧转体桥没有进行配重，桥梁不平衡力矩为8 761.8 kN·m。北侧梁的摩阻力矩小于南侧梁的摩阻力矩，且北侧桥梁的不平衡力矩大于南侧桥梁的不平衡力矩。在列车振动导致的球铰转动力矩分析中，取摩阻力矩较小的北侧梁球铰进行分析。

对表1中的时程记录利用Midas进行有限元分析，得到列车振动引起的最大转动力矩，见表5。

表5 列车振动引起的球铰最大转动力矩 kN·m

撑脚所能提供的最大力矩MC的计算可采用下列各式［6］

式中:fsc为钢管混凝土的组合轴压比强度设计值;fck，fc分别为混凝土的轴心抗压强度标准值和设计值;f为钢材的抗拉、抗压和抗弯强度设计值;fy为钢材的屈服强度;ξ0为构件截面含钢率;As，Ac分别为钢管和混凝土的截面面积;ηs，ηc分别为计算系数;Asc为钢管混凝土的截面面积;Fsc为钢管混凝土的压力设计值。

通过上式求得Mc为350 072 kN·m。代入数据可知MC+MZ＞＞MG+M。因此在桥梁转动前及转动过程中，即使有列车通过，梁体也不会发生倾覆。

进一步对梁体由于列车诱发的地面振动而产生的晃动情况进行分析。由记录的加速度时程曲线可知，加速度的方向随着时间在不断变化。在这种变化过程中对球铰产生的纵向转动力矩若足够大，即满足M＞MG+MZ的条件，此时梁体就会发生晃动。取最不利的南侧转体桥进行受力分析，参见图4(b)。通过同样的模拟及计算可知MZ+MG＞＞M。因此在转体过程中，即使在有列车通过的情况下，球铰不会发生转动，梁体也不会发生晃动。