基于实测数据修正的徐变预测模型在铁路桥预拱度计算中的应用
2014-05-04姜嫚
姜 嫚
(中铁第四勘察设计院集团有限公司,湖北武汉 430063)
由于铁路桥梁载重量大、列车运行速度快、对舒适、美观和安全的敏感度较高,所以,预应力混凝土铁路桥预拱度设置的准确性显得尤为重要。
在目前的预应力桥梁建设中,预拱度的设置一般依靠经验或者在考虑徐变时使用理论预测模型,而理论模型主要是根据实际工程情况对混凝土材料的徐变进行预测,预测精度受混凝土诸多因素的影响,往往偏离实际较大[1-3]。
本文针对混凝土徐变影响因素多样这一特点,以试验桥段的短期徐变试验数据为基础,对该铁路桥适用的徐变预测模型展开探讨,提出指导施工的建议。
1 工程背景与试验设计
1.1 工程背景
郑焦城际铁路跨连霍高速公路特大桥是悬臂现浇预应力混凝土连续梁桥,全桥长243.7m,计算跨径242 m,建筑总宽度12.48 m,梁体混凝土强度为C50。结构形式为三向预应力混凝土连续箱梁桥,梁体为单箱单室、变高度、变截面结构。桥梁立面布置如图1。

图1 郑焦城际铁路桥连续梁立面(单位:m)
混凝土配合比见表1。水泥采用郑州天瑞水泥厂的P.O42.5硅酸盐水泥;粉煤灰为禹州通达Ⅰ级粉煤灰;矿粉为济源国泰S95级矿粉;砂为鲁山河沙;石料为贾峪碎石,粒径为5~10 mm和10~20 mm(级配比例为1∶4);外加剂采用山西黄腾HT-HPC聚羧酸高性能减水剂。

表1 混凝土的配合比 kg/m3
1.2 试验描述
为了准确地计算桥梁预拱度,排除直接输入参数对桥梁预拱度计算的影响,需要通过试验改进徐变预测模型,更加精确地预测徐变变形。试验是通过现场短期徐变试验,测量徐变应变,通过试验数据重新计算徐变系数[4]。
短期徐变试验通过埋设元件测量桥梁施工过程的应力应变情况,结合工程参数计算徐变变形,并根据徐变变形结果为徐变预测模型的改进提供数据支持。徐变应变是元件测量到的总应变减去弹性应变、收缩应变、温度效应变形、湿度应变和其他应变之后的结果,弹性应变可以根据工程参数计算,因此只需找到其他剩余应变的总和,即可得到徐变应变。总应变ε总为

式中,εσ为弹性应变与徐变应变之和,而ε0表示剩余应变之和,设它为参照应变,徐变计算的关键是找到参照应变。因此试验设计的原则是通过一定方法测量参照应变和总应变,并计算弹性应变,从而得到一组短期徐变应变数据,为修正徐变预测模型提供数据支持。
为了得到参照应变ε0,在试验进行的同时按照主梁的标准浇筑两个额外的参照梁,与主梁传感器埋设位置和方向一致布置应变计。为了使其不产生弹性变形和徐变变形,梁上不施加任何应力,同时为了消除其他因素的影响,将参照梁置于施工现场附近,且均选取同一时间的读数为准。
2 基于实测数据的CEB-FIP 1990[5]徐变预测模型修正
2.1 建立有限元模型
运用结构有限元分析方法建立跨连霍高速公路特大桥有限元计算模型。如图2所示。

图2 跨连霍高速公路特大桥有限元计算模型
2.2 几种徐变理论预测模型与实测数据的差异性分析
混凝土徐变是随着时间不断变化的。以往的研究表明,混凝土结构在加载后的最初几天徐变进展较快,并在60 d以内呈现高速增长趋势,之后速率逐渐变慢并在若干年之后趋于稳定,这很符合指数函数的特征。考虑到时间以及预测数据要参与后期预拱度计算等原因,短期试验测量60 d应力应变数据,测量频率为1次/d。
实测徐变系数(图3)是在实测应力和应变值的基础上计算得到的近似值,其中计算参照应变时还使用到上文所述无应力作用自由小梁的对比数据,在计算弹性应变时考虑到不同阶段的荷载变化情况,并参考工程荷载设计资料。舍弃部分不合格点和测量误差较大点以及加入补测点之后得到的一系列徐变系数实测数值。60 d的徐变系数最大值达到0.940。数值的变化基本符合平滑、无较大突变的特点,呈现从小到大逐次增加的类指数函数趋势。
从实测值可以得到桥梁短期试验实际徐变系数的变化规律,将几种以徐变系数为考虑因素的徐变预测理论模型运用到实际工程中可以得到一系列的徐变系数预测结果,当这些结果彼此存在较大差异时,可以选择与实测结果较吻合的模型作为模型修正的基础模型。
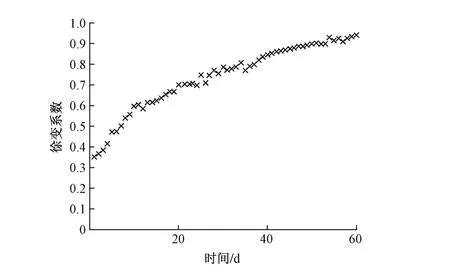
图3 实测徐变系数
图4中对比了实测值计算所得徐变系数值与理论模型中的徐变系数,其差异系数见表2。

图4 徐变系数对比

表2 实测徐变系数与几种模型的差异系数
从表2可见,CEB-FIP 1990预测模型与实测徐变系数系列点的差异系数为3.20%,在所有模型中最小,即预测效果最好。因此可将CEB-FIP 1990预测模型作为通过短期试验实测结果拟合徐变系数的函数,并以此为修正徐变系数预测模型的基础[6]。
2.3 徐变系数拟合与模型修正
利用最小二乘法原理,使用作图程序软件对实测60 d徐变系数拟合,结果如图5所示。

图5 徐变系数函数拟合结果
将实测的徐变系数序列点按照CEB-FIP 1990徐变系数预测模型中徐变系数形式函数y=a×[x/(b+x)]c进行拟合,得到3个系数

所以,通过短期徐变试验数据拟合得到的徐变系数函数为

得到修正的徐变系数函数,即可以重新预测混凝土的徐变变形,并最终可用有限元方法重新计算桥梁预拱度。
3 修正徐变预测模型在桥梁预拱度设置中的应用
3.1 模型预拱度计算结果
现阶段徐变预测模型比较直接的应用,是对实际在建桥梁的预拱度控制,将基于短期试验修正的徐变预测模型运用到MIDAS/CIVIL 2011软件中计算得到该城际铁路(65+112+65)m连续梁桥预拱度值,并与原徐变预测模型的计算值进行对比,如图6所示。
图6显示修正后模型的预拱度计算值峰值点为26.39 mm,谷点为-24.12 mm,在实际施工过程中设置预拱度难度较小,适合施工。

图6 修正模型与原模型预拱度计算值
3.2 模型可靠性分析
预拱度的设置是为了抵消桥梁在施工完成后的长期变形产生的下挠,为了研究徐变预测模型所计算的预拱度设置结果是否能达到这一工程目的,在现场选择若干点位采集主梁在计算时间范围内的标高变化规律,并计算下挠值,与计算预拱度对应比较,可以近似地验证模型的准确性。
该城际铁路特大桥已经全线合龙。对完成合龙后的桥梁高差变化(下挠情况)测量,并与模型计算的相同时间的桥梁位移变化值比较,可以作为验证预测模型可靠度的数据依据。
根据上面所述方法,对每个已浇筑混凝土梁段进行下挠值测量,并将所测结果与计算模型中对应工况的累积竖向位移值(高程差)进行对比,从而判断修正模型的可靠性。对于实际工程,在此假定弹性变形与模拟一致,造成理论计算的下挠值与实测值存在误差的原因只有混凝土的徐变。图7为不同施工梁段完成后CEB-FIP 1990模型和修正模型时间一致时计算的累积竖向位移与实际工程中测得的梁下挠值(即实测高程差)。

图7 模型累积位移结果对比
从图7可以看到实际测量的高程差与修正预测模型所计算的累积竖向位移具有很高的吻合度,而与CEB-FIP 1990模型的计算结果有所差别。这是由于自建模型很好地考虑了工程实际数据,尤其是合龙阶段徐变变形已经达到总徐变变形的50%左右,这种变化的趋势和规律显示,通过短期实测徐变变形数据重新建立的徐变预测模型在预拱度计算时具有优势,可以达到更好的工程效果,具有较高的工程可靠性。
3.3 方法总结与施工建议
本文对预拱度设置计算的方法可总结为以下几个步骤。
1)埋设元件,测量1~3月的短期徐变试验数据
在桥梁施工阶段埋设应力计和应变片,采集的数据的处理要舍弃异常点,尽量保证数据的准确性和真实性。本文中通过设置无应力自由小梁来过滤其他应变的方法计算徐变变形,并使用徐变系数的变化参与对比。
2)选择合适的基础模型
通过实测数据计算桥梁在短期徐变试验的徐变系数,并通过与备选徐变预测模型的对比,确定一个与工程实际的徐变变化规律吻合度较高的模型,作为通过实测数据拟合徐变系数修正的基础模型。本文在数据的吻合程度不能直接观察得到时,使用修正的差异系数百分比来表示这一程度,差异系数越小,吻合程度越高。
3)建立修正模型
对实测的徐变系数进行拟合,得到徐变系数函数,并依此对基础模型进行修正,建立修正预测模型。
4 结语
本文基于桥梁短期试验数据,计算徐变系数序列值,通过差异系数分析,选取徐变预测模型作为拟合的基本函数,再通过试验数据对函数进行修正,最后将修正的函数用于桥梁预拱度的软件计算中。全文得到如下结论:
1)对短期试验得到的应变(应力)数据进行分析,重新计算徐变系数序列,采用最小二乘法原理运用软件按照CEB-FIP 1990模型徐变系数函数基本形式,将短期试验数据拟合为徐变系数函数,修正基于实际工程数据排除各种影响因素的徐变预测模型。
2)将修正的模型应用到工程桥梁预拱度的计算上,得到最为贴近该城际铁路桥梁的预拱度值,并验证修正后模型的可靠性,同时总结基于短期徐变试验数据对徐变预测模型进行改进并计算预拱度的方法,为今后铁路桥的建设提供理论指导。
[1]陈守辉.大跨度预应力混凝土连续箱梁桥收缩徐变效应分析[J].铁道建筑,2009(8):15-17.
[2]丁文胜,吕志涛,孟少平,等.混凝土收缩徐变预测模型的分析比较[J].桥梁建设,2004(6):13-16.
[3]邵旭东.桥梁工程[M].北京:高等教育出版社,2004.
[4]张运涛,孟少平,惠卓,等.苏通大桥连续刚构桥主梁混凝土徐变试验研究[J].公路交通科技,2010(4):101-104.
[5]CEB-FIP.CEB-FIP Model Code for Concrete Structures 1990[S].Paris:Comite Euro-International du Beton Federation International de la Preconstrainte,1990.
[6]潘钻峰,吕志涛,刘钊,等.高强混凝土收缩徐变试验及预测模型研究[J].公路交通科技,2010(12):10-15.
