基于模拟退火算法的换热网络双层优化方法

彭富裕，崔国民，陈家星

（上海理工大学 新能源科学与工程研究所，上海 200093）

换热网络作为化工过程中重要的能量回收环节，其设计的合理性和高效性将直接关系到系统的整体性能。1969年，Masso等［1］首次严格定义换热网络综合问题，即充分利用工艺物流的能量，使得热回收量最大或经济费用投入最小。以夹点技术［2］为代表的热力学方法凭借其物理意义清晰、操作简单的优势得到了广泛应用［3-5］，但此类方法分步优化的特点不能同时兼顾换热器数、换热面积及能量回收之间的权衡关系，只能得到接近最优的换热网络设计。基于数学理论提出的换热网络同步综合模型由于同时涉及代表结构的整型变量和决定费用大小的连续变量优化，属于典型的混合整数非线性规划问题，目标函数呈现的严重非凸非线性使得确定性优化方法的求解过程极易陷入某个局部最小解，而无法找到理论上的全局最优解［6-7］。此外，Furman等［8］证明换热网络综合问题属NP-hard范畴，求解的可操作性严重受制于网络规模的大小。

基于随机技术的启发式算法对目标函数的要求相对宽松，并凭借其可操作性强和计算效率高等优点开始受到越来越多的关注［9-13］。换热网络的优化过程既包括换热器和公用工程面积费用以及公用工程费用的连续变量优化，同时也涉及到代表换热器有无的0-1整型变量优化。单从整型变量角度进行分析，结构优化过程属于大规模的组合优化问题，由于各个网络结构之间并不存在任何联系，因此现有的算法通常以费用或能量目标作为判断结构优劣的标准，将进化的迭代次数或目标函数的变化情况作为最终的收敛判据。而固定结构下的连续变量优化的实质是解决如何高效跳出局部极值陷阱问题，随着网络规模的扩大，优化变量的数目也逐渐增加，要求算法具有较强的全局搜索能力和计算效率。Lewin等［14-15］将遗传算法应用到换热网络的结构优化中，以最大能量回收为目标优化特定的网络结构，再反馈到遗传算法的适应函数进化网络结构。随后，这种采用遗传算法优化外层结构的策略又分别与微分进化、模拟退火和粒子群等算法相结合应用于换热网络的最优化研究［16-19］。但随机算法的本质却决定了此类算法不能搜到理论上的全局最优解。

与其他随机算法相比，模拟退火算法的一大优势在于理论较为完善，在条件合适的前提下，其全局收敛性可以得到保证［20］。在模拟退火算法的基本思想提出之后，Kirkpatrick等［21］最早将其成功应用于组合优化问题。随后，Dolan等［22-23］又将该算法引入到换热网络的设计中，用于求解同时具有离散变量和连续变量换热网络综合问题，以Metropolis准则同步更新对应的换热网络结构和换热量分配。在此基础上，Athier等［24］尝试在模拟退火机制进化外层结构的同时，采用现有非线性规划技术优化内层连续变量，旨在提高整个算法的效率，解决工业级别的换热网络综合问题。

本工作借鉴双层优化的思想，采用换热网络的分级超结构模型，外层以费用目标作为判断结构优劣的标准，将模拟退火算法应用于代表网络结构的整型变量优化，通过特定的邻域搜索方式及结构约束逐步进化更新网络结构；内层费用连续变量优化同样采用模拟退火算法进行，旨在为实现换热网络的全局最优化提供一种新的方法。

1 换热网络优化的数学模型

1.1 换热网络模型

以2股热流体和3股冷流体为例，无分流的Grossmann分级超结构［3］见图1。一般来说，换热网络的级数k（k=1，2，…，Nk）的取值不大于max（NH，NC）。级数确定后，不同流股间最多的匹配次数为Nk，换热器个数最多可达到NH×NC×Nk。

1.2 目标函数及约束条件

针对由i股热流体、j股冷流体组成的k级换热网络，若以经济费用最小为目标，则优化的目标函数为：

约束条件主要包括：单股流体热平衡、冷热流股可行出口温度、冷热公用工程热平衡及非负约束。

1）单股流体热平衡：

2）冷热流股可行出口温度：

3）冷热公用工程热平衡：

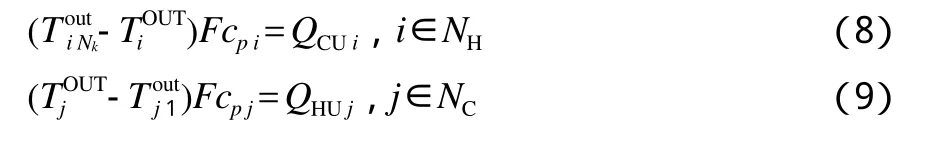
还隐含包括以下连续变量在传热计算中的非负约束。

1）换热面积非负约束：

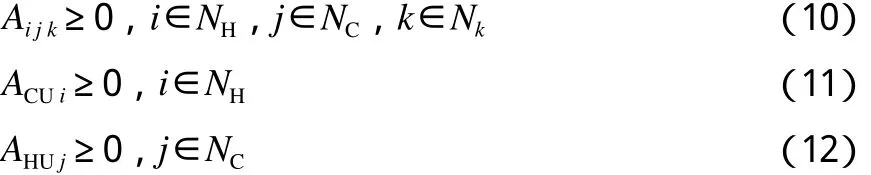
2）换热量非负约束：

依据模型中的假设，冷热流股逆流布置。传热计算中，单个换热器满足以下热平衡关系：

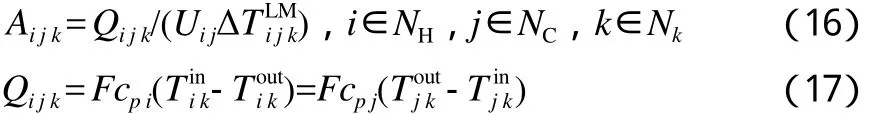
为了防止出现温度交叉和换热面积无限大的情况，必须定义相应的最小换热温差约束：

2 换热网络双层优化策略

换热网络结构优化的实质是对代表换热器有无的0-1整型变量的优化，考虑到每种整型变量的组合形式都将对应一种特定的换热网络结构，随着换热网络规模的扩大，求解过程也变得异常复杂。采用模拟退火算法优化换热网络结构时，将代表结构的特定整型变量组合看作退火过程中的状态点，通过对比不同结构的优劣决定是否接受新状态点。对于特定结构，由于费用目标是判断结构优劣的标准，因此要求内层的连续变量算法需具有较强的全局搜索能力，才能保证结构优劣判据的有效性。从全局最优化的角度来讲，模拟退火算法允许以一定的概率接受“差”的试探点，从而可以避免结构优化和费用优化过早地陷入某个局部最小解，只要相关控制参数设置合理，可以得到问题的相对全局最优解。

2.1 内层连续变量优化

对于固定结构下的换热网络连续变量优化，关键在于如何有效地跳出局部最小解陷阱，而内层算法的计算效率也将直接影响到外层结构的进化效率，因此在保证计算精度的前提下应尽可能缩短计算时长。模拟退火算法的冷却进度表控制着算法的全局收敛性和计算效率，其中的主要参数包括初始温度（T0）、降温函数、温度迭代长度（L）及终止准则。

2.1.1 邻域搜索方式

模拟退火算法优化换热网络费用连续变量，由式（1）可知，特定结构下由换热面积及公用工程使用带来的费用可作为优化过程中的某个状态点。由于大量约束条件的存在，给新试探点的产生带来一定困难，采用构建辅助函数的方法将原问题转化为无约束问题后，也存在相惩罚因子难以确定等问题。因此，考虑将流股间匹配的换热量（Qijk）作为优化变量，利用潜在的热平衡约束条件，保证每次新的状态点均在可行域中产生，具体操作如下。

1）计算各热冷流股的换热潜能Qpi和Qpj：

2）对于某个换热器（zijk），给定确定换热量增减的概率参数（β，0≤β≤1），产生［0，1］均匀分布的随机数r和r′。

3）若r≥β，则

且

增加流股匹配换热量。

4）若r<β，则

且

减少流股匹配换热量。

以上邻域搜索方法可以保证新生成的状态点不违反能量守恒约束，均在可行域中。对于约束式（18）和（19），可以规定当出现温度交叉时，该冷热流股为不合理匹配，令zijk=0，作无效匹配处理。

2.1.2 初始温度和温度迭代长度

T0和L是影响模拟退火全局收敛性的重要因素。实际应用中，常将L设为一个常数，即在每一温度下，均迭代相同的次数。随后，可通过取值计算估计和统计推断估计来确定与L相匹配的T0，具体计算过程如下：

1）给定温度变化常量ΔT和T0的估计值、初始温度下解的接受比率的预期值γ0（接近于1）、收敛精度ε0以及每一温度下的L。令迭代计数k0=1。

2）记录L步迭代后接受的状态个数L′，该温度下接受的比例Rk0=L′/L。

3）若─Rk0-γ0─<ε0，则停止计算，T0即为合适的初始温度；否则，

当Rk0-1<γ0且Rk0<γ0时，k0=k0+1，T0=T0+ΔT，转回步骤2）；

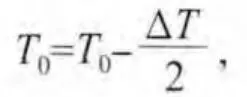
2.1.3 温度下降函数和终止准则

温度下降方法是影响模拟退火算法全局搜索性能的又一个重要因素。在实际应用中，往往采用较为直观的降温方式，即Tk+1=αTk，其中α为0到1之间的常数，每次温度都以相同的比率下降，α越大则温度下降越慢。理论上，当退火温度为零时，模拟退火算法终止。但在实际应用时，往往采用一些比较直观的终止准则，即T<ε。

2.2 外层整型变量优化

单从变量形式上看，由特定整型变量组合代表的换热网络结构之间并不存在任何联系，故选取对应结构下的最优费用作为判断结构优劣的标准。同样，模拟退火算法用于换热网络的结构优化也需要确定相应的冷却进度表：初始温度（T0out）、降温函数、温度迭代步长（L0out）和终止准则。

当前结构下生成新试探结构的过程对算法的整体效率有着重要的影响，不仅要求实现整个求解域的搜索过程，还要尽可能排除明显较“差”的换热网络结构以提高计算效率。因此，在生成新试探结构时，可以增加一些相应的约束条件，具体操作如下。

1）给定确定换热器增减的概率参数βout，生成［0，1］分布的随机变量rout。

2）若rout≥βout，从已有换热器中随机抽取一项（不包括公用工程），令zijk=0，删去一个换热器。

3）若rout<βout，从换热网络中随机抽取任一不存在换热器的位置（不包括公用工程），令zijk=1，增加一个换热器。

新试探结构的生成过程中可设置最小总换热器个数约束，而对单股流体也可设置最大换热器个数约束，以防止出现换热器总数过少或某股流体匹配过多换热器的不合理结构。此外，对于不同的换热网络设计问题，通过观察单股流体的温位水平，可以限制“过冷”热流体与“过热”冷流体之间的禁忌匹配。

Lout可取固定步数，由于每个结构都对应一次费用连续变量的全局优化过程，为了提高计算效率，结构优化的初始温度可采用估算所得，即T0out=δ(Fmax-Fmin)，δ为充分大的数。同时，温度下降方式和终止准则沿用Tk+1out=αoutTkout和Tout<εout。

3 算例与分析

3.1 算例一

选用文献［25］中的6×4算例，该换热网络由6股热流体和4股冷流体组成，具体的物流参数详见表1，换热器面积费用计算公式为60A $/a，热公用工程费用系数为100 $（kW·a），冷公用工程费用系数为15 $（kW·a）。

表1 算例一的物流参数Table 1 Problem data for case 1

选取网络级数为4，内层连续变量优化相关参数为：β=0.95，充分利用冷热流股换热潜能， L=500，T0=2×106，ΔT=5×105，γ0=0.95，ε0=1×10-6，α=0.75，ε=1。外层整型变量优化相关参数为：βout=0.5，具有相同的概率增减换热器； T0out=105， Lout=60，αout=0.9。在生成试探结构时增加以下两个约束：

1）初始换热器数估计值为8，规定热流股上最大换热器数为3、冷流股换热器数为4（不包括公用工程）。

2）热流股4的温位水平较低，认为属“过冷”热流体，限制其不参与换热匹配。

采用Fortran编程，计算机CPU为Intel（R）Core（TM）i5-2320，主频3.00 GHz，计算时长为143 h。优化结果见表2，换热网络结构见图2。

由表2可知，基于模拟退火算法的结构优化的实质是各个换热网络结构之间的相互变换，并逐步收敛于费用较低的结构的过程，可以搜索到较多的较优结构。再借助模拟退火算法在连续变量优化方面的较强全局搜索能力可以得到优于文献结果的换热网络设计。此外，由图2可知，对于热流股4由于增加了不参与换热匹配的约束，只能用公用工程冷却，而单股流体的最大换热器数约束也可以有效地将换热网络结构限制在合理的范围之内。

表2 算例一的优化结果Table 2 Solutions to case 1

图2 算例一的优化结构Fig.2 Results for case 1.

3.2 算例二

算例二选自文献［28］，由8股热流体和7股冷流体组成，具体物流参数见表3。与算例一的不同在于计算投资费用时考虑了固定投资费用，换热器面积费用的计算式为8 000+500A0.75$/a，热公用工程费用系数为80 $（kW·a），冷公用工程费用系数为10 $（kW·a）。

选取换热网络级数为2，内层连续变量优化相关参数为：β=0.95，L=500，T0=106，ΔT=106，γ0=0.95，ε0=1×10-6，α=0.75，ε=1。外层整型变量优化相关参数为：βout=0.5，T0out=2×106，Lout=50，αout=0.9。此外，在生成试探结构时增加以下两个约束：

1）初始换热器数估计值为9，规定热流股上最大换热器数为4、冷流股器数为3（不包括公用工程）。

2）将热流股7与冷流股4定为固定匹配，不参与其他流体的匹配也可以各自达到目标温度。

采用Fortran编程，计算机CPU为Intel（R）Core（TM）i5-2320，主频3.00 GHz，计算时长为183 h。优化结果见表4，换热网络结构见图3。

由表4可知，基于模拟退火算法的双层优化方法可以优化得到优于文献结果的换热网络设计。由图3可知，虽然没有针对冷流股7增加相应的匹配限制约束，但由于该流股属于温位较高的冷流体，不利于与温位较低的热流体进行匹配换热，因此得到的优化结果中该流股通过公用工程加热至目标温度。

此外，根据欧拉广义网络理论对换热网络换热单元个数的估计，算例一换热单元应为11个，但实际优化得到的换热单元分别（对应图4中的两个结果）为14和15个；而算例二的理论换热单元为16个，实际换热单元个为17和18个。设备投资费用由固定投资费用和面积费用两部分组成。由此可知，当面积费用系数B=1且固定投资费用计算常数（CF）相对较小时，换热网络设计受换热单元个数的限制也相对较小。反之，目标函数将受制于换热网络的换热单元个数限制，优化过程更倾向于接受个数较少的“大面积换热器”而不是个数众多的“小面积换热器”。算例一的固定投资费用为0、B=1，因此受换热单元个数的限制较小，得到的优化结果换热单元个数均远大于理论值。而算例二由于存在较大的固定投资费用且B=0.75，因此最优的换热网络结构更倾向于换热器更少的结构。

表3 算例二的物流参数Table 3 Problem data for case 2

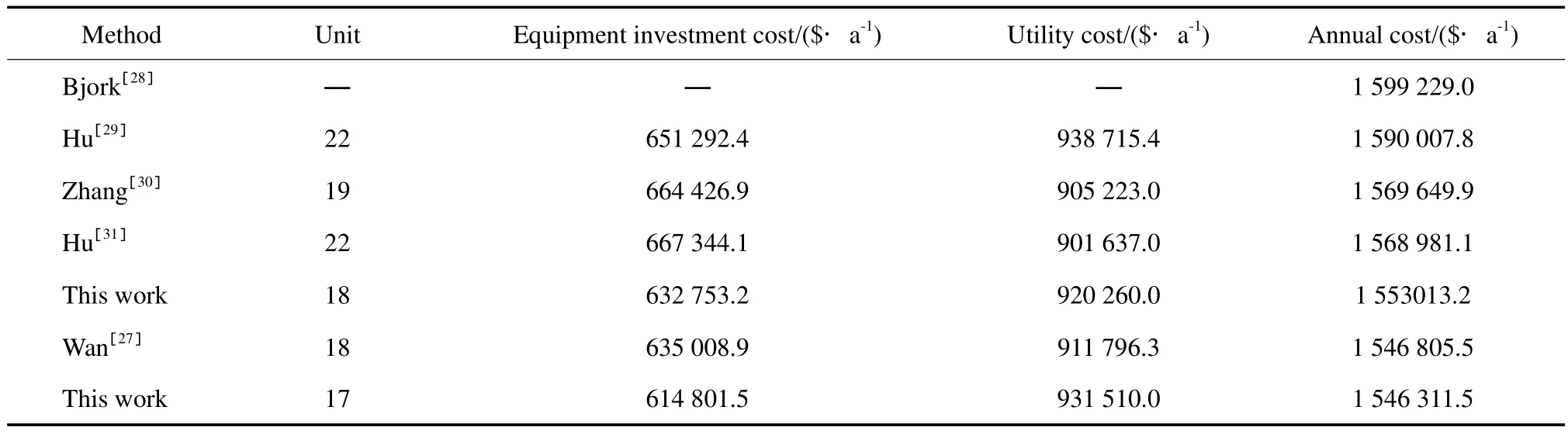
表4 算例二的优化结果Table 4 Solutions to case 2

图3 算例二的优化结构Fig.3 Results for case 2.

3.3 讨论

效率和精度是评价优化方法的两个重要指标。双层优化的思想将同时具有整型变量和连续变量的混合整数非线性规划问题分为外层整型变量优化和内层连续变量优化两个过程。相对于整型变量的全局最优化，针对连续变量的全局最优化技术相对成熟，从计算精度角度来看，无论是采用等效松弛处理非凸项的确定性方法还是众多随机性方法，都可以有效实现连续变量的全局最优。整型变量的全局最优化一直以来都是优化理论中的难点问题，代表换热网络结构的整型变量优化，其实质是复杂的组合优化问题，对于由NH股热流体和NC股冷流体组成的Nk级换热网络，理论上存在2NH×NC×Nk种可能的结构组合，而随着换热网络规模的扩大和优化变量的增加，易导致组合爆炸问题的发生，从而大幅降低问题的可操作性，进而影响优化的效率。

因此，为了同时兼顾双层优化方法的效率和精度，要保证外层算法在有限的时间内尽可能试探更多的结构组。本工作从传热角度添加额外结构约束的方法旨在缩小搜索域，减少对部分较差结构的计算时间。但由于模拟退火算法中新试探点是在当前解的邻域范围内通过随机扰动产生的，因此这种方法也可能会限制结构产生过程中结构与结构之间的过渡过程。今后的研究可致力于更有效的结构约束的确定。为了提升整个算法的计算效率，内层连续变量优化要在保证全局收敛性的前提下，尽可能地缩短单个结构的优化计算时间，因此可以考虑采用更高效的连续变量全局最优化方法。

4 结论

1）针对同时存在整型变量和连续变量的换热网络优化问题，提出一种基于模拟退火算法的双层优化方法，分别处理两种变量形式的优化过程。

2）外层算法优化选取费用目标作为判断结构优劣的标准，通过随机扰动的方式不断产生新的结构，并借助模拟退火机制不断进化换热网络结构；内层算法通过模拟退火算法对固定结构下的连续变量进行优化，再将得到的最优解反馈到外层算法，作为结构优化的判断标准。

3）通过两个具体算例证明，模拟退火算法可有效处理整型变量形式的结构优化，找到较优结构，而双层优化方法可以有效处理具有整型变量和连续变量两种变量形式的换热优化问题，取得较好的换热网络设计。

符 号 说 明

A 换热器面积，m2

B 投资费用计算常数

C 投资和运行费用计算常数

CF固定投资费用计算常数

Fmax，Fmin目标函数的最大值和最小值

Fcp热容流率，kW/℃

k0初始温度计算迭代计数

L 温度迭代步长

Q 换热量，kW

Qp换热潜能，kW

Rk0解的接受比例

r ［0，1］内均匀分布的随机数

T 温度

T0初始温度

ΔT 温度变化常量

ΔTmin最小传热温差

ΔTLM对数平均温差

U 换热系数，kW/（m2·℃）

z 换热器有无的0-1变量

α 温度下降系数

β 概率参数

γ0初始温度下解的接受比率的预期值

ε 终止温度

ε0收敛精度

上角标

IN 流股入口

in 单个换热器入口

OUT 流股出口

out 单个换热器出口

k 迭代次数

下角标

CU 冷公用工程

HU 热公用工程

i 热流股，i=1，2，…，NH

j 冷流股，j=1，2，…，NC

k 换热网络级数，k=1，2，…，Nk

out 外层算法

［1］Masso A H，Rudd D F.Synthesis of System Designs：Ⅱ.Heuristic Structuring［J］.AIChE J，1969，15（1）：10-17.

［2］Linnhoff B，Flower J R.Synthesis of Heat Exchanger Networks：Systematic Generation of Energy Optimal Networks［J］.AIChE J，1978，24（4）：633-654.

［3］Rivedi K K，Oeill B K，Roach J R，et al.A New Dual-Temperature Design Method for the Synthesis of Heat Exchanger Networks［J］.Comput Chem Eng，1989，16（6）：667-685.

［4］Fraser D M.The Use of Minimum Flux Instead of Minimum Approach Temperature as a Design Specification for Heat Exchanger Networks［J］.Chem Eng Sci，1989，44（5）：1121-1127.

［5］Trivedi K K，Oeill B K，Roach J R，et al.Systematic Energy Relaxation in MER Heat Exchanger Networks［J］.Comput Chem Eng，1990，14（6）：601-611.

［6］Yee T F，Grossmann I E.Simultaneous Optimization Models for Heat Integration：Ⅱ.Heat Exchanger Network Synthesis［J］.Comput Chem Eng，1990，14（10）：1165-1184.

［7］胡向柏，崔国民，涂惟民.复杂换热网络MINLP中的非线性特性分析［J］.工程热物理学报，2012，33（2）：285-287.

［8］Furman K C，Sahinidis N V.Computational Complexity of Heat Exchanger Network Synthesis［J］.Comput Chem Eng，2001，25（9/10）：1371-1390.

［9］Chakraborty S，Ghosh P.Heat Exchanger Network Sythesis：The Possibility of Randomization［J］.Chem Eng J，1999，72（3）：209-216.

［10］Pariyani A，Gupta A，Ghosh P.Design of Heat Exchanger Networks Using Randomized Algorithm［J］.Comput Chem Eng，2006，30（6/7）：1046-1053.

［11］Gupta A，Ghosh P.A Randomized Algorithm for the Ef fi cient Synthesis of Heat Exchanger Networks［J］.Comput Chem Eng，2010，34（10）：1632-1639.

［12］Lin B，Miller D C.Solving Heat Exchanger Network Synthesis Problems with Tabu Search［J］.Comput Chem Eng，2004，28（8）：1451-1464.

［13］Silva A P，Ravagnani M A S S，Biscaia E C，et al.Optimal Heat Exchanger Network Synthesis Using Particle Swarm Optimization［J］.Optim Eng，2010，11（3）：459-470.

［14］Lewin D R，Wang H，Shalev O.A Generalized Method for HEN Synthesis Using Stochastic Optimization：Ⅰ.General Framework and MER Optimal Synthesis［J］.Comput Chem Eng，1998，22（10）：1503-1513.

［15］Lewin D R.A Generalized Method for HEN Synthesis Using Stochastic Optimization：Ⅱ.The Synthesis of Cost-Optimal Networks［J］.Comput Chem Eng，1998，22（10）：1387-1403.

［16］Yerramsetty K M，Murty C V S.Synthesis of Cost-Optimal Heat Exchanger Networks Using Differential Evolution［J］.Comput Chem Eng，2008，32（8）：1861-1876.

［17］Khorasany R M，Fesanghary M.A Novel Approach for Synthesis of Cost-Optimal Heat Exchanger Networks［J］.Comput Chem Eng，2009，33（8）：1363-1370.

［18］Luo Xing，Wen Qingyun，Fieg Georg.A Hybrid Genetic Algorithm for Synthesis of Heat Exchanger Networks［J］.Comput Chem Eng，2009，33（6）：1169-1181.

［19］Huo Zhaoyi，Zhao Liang，Yin Hongchao，et al.Simultaneous Synthesis of Structural-Constrained Heat Exchanger Networks with and Without Stream Splits［J］.Can J Chem Eng，2013，91（5）：830-842.

［20］Dekkers A，Aarts E.Global Optimization and Simulated Annealing［J］.Mathematical Programming，1991，50（1/3）：367-393.

［21］Kirkpatrick S，Gelatt C D，Vecchi M P.Optimization by Simulated Annealing［J］.Science，1983，220：671-680.

［22］Dolan W B，Cummings P T，LeVan M D.Process Optimization Via Simulated Annealing：Application to Network Design［J］.AIChE J，1989，35（5）：725-736.

［23］Dolan W B，Cummings P T，LeVan M D.Algorithmic Ef fi ciency of Simulated Annealing for Heat Exchanger Network Design［J］.Comput Chem Eng，1990，14（10）：1039-1050.

［24］Athier G，Floquet P，Pibouleau L，et al.Synthesis of Heat-Exchanger Network by Simulated Annealing and NLP Procedures［J］.AIChE J，1997，43（11）：3007-3020.

［25］Ahmad S.Heat Exchanger Networks：Cost Trade-Offs in Energy and Capital［D］.Manchester：Manchester Institute of Science and Technology，1985.

［26］Ravagnani M A S S，Silva A P，Arroyo P A，et al.Heat Exchanger Network Synthesis and Optimization Using Genetic Algorithm［J］.Appl Therm Eng，2005，25（7）：1003-1017.

［27］万义群，崔国民，彭富裕，等.基于温差原则的换热网络分步综合策略［J］.石油化工，2013，32（9）：996-1003.

［28］Bjork K M，Pettersson F.Optimization of Large-Scale Heat Exchanger Network Synthesis Problems［C］//Hamza M H，ed.Palm Springs：Proceedings of the IASTED International Conference on Modeling and Simulation，2003：313-318.

［29］胡向柏，崔国民，涂惟民，等.网络填充函数法的全局优化［J］.化学工程，2011，39（1）：28-31.

［30］张勤，崔国民，关欣.基于蒙特卡罗遗传算法的换热网络优化问题［J］.石油机械，2007，35（5）：19-22.

［31］胡向柏，崔国民，许海珠，等.换热器优化顺序对换热网络全局优化的影响［J］.化工进展，2012，31（5）：987-1003.