基于改进的Grey－AHP的机械零部件供应商评价

孙丽琴 袁希腾 马金麟

SUN Li－qin YUAN Xi－tengMA Jin－lin

（江苏大学汽车与交通工程学院，江苏 镇江 212013）

（School of Automotive and Traffic Egineering，Jiangsu University，Zhenjinag，Jiangsu 212013，China）

机械制造行业属于加工装配型产业，零部件供应商数量众多，供应商评价是机械制造企业对供应商进行管理、监督等活动的基础和标准，对实现企业利润最大化和产品安全有着举足轻重的作用［1］。

在机械制造企业的供应商管理活动中，对零部件供应商评价不客观、选择失误，易导致增加库存成本、出现缺货或残次品、延迟交货期，甚至出现中断生产计划等不良后果，对企业带来严重损失，良好的供应关系可有效避免不良现象的出现，保证良好的生产秩序，确保企业在竞争中占据优势，集中精力发展核心业务。

机械制造企业需要一个科学的评价体系，对零部件供应商进行全面客观的评价，选择正确的供应商。同时，通过建立供应商评价体系，为企业和供应商提供一个相互交流的平台，促进企业和供应商的共同发展。

1 供应商评价体系的建立

通常，产品加工和开发设计两个环节决定了产品品质，优良的产品需要科学的设计和精密的加工。因此，对机械制造企业零部件供应商的评价从两方面进行：生产过程和开发设计过程。结合某包装机械制造企业的零部件供应商评价标准，建立生产过程和开发设计过程的评价体系，见图1，单项指标的评价标准，参照表1。

根据对生产过程和设计开发过程的综合评价符合率所在区间将供应商分为A、B、C 3个等级，只有生产和开发设计两个过程的评价等级均达到A级的零部件供应商才有资格成为该企业的合格供应商，见表2。

2 评价模型的建立

该供应商评价体系存在以下不足：① 进行求和时所有指标总分值都是10分，即每个末级指标权重相同，不同的指标相对重要程度是不同的，如此设置不科学。② 将评分结果简单的进行求算术平均值，由于各指标的意义和量纲的不同，很多指标无法量化或完全量化，当多个评审员对同一指标进行评价时，会产生主观上的误差，简单的求算术平均数会增大评分误差。

图1 零部件供应商评价指标Figure 1 Machinary－parts supplier evaluation index

表1 评分参照表Table 1 Score reference table

针对该机械制造企业供应商评价体系的不足，提出了采用改进的层次分析法计算各项评价指标的权重，利用不同层次三角白化权函数决策，确定灰色评价权矩阵，对供应商进行评价［2］。

表2 定级参照表Table 2 Rank reference table

表2 定级参照表Table 2 Rank reference table

符合率为各末级指评价评分值的算术平均值与单项总分（10）比值乘100%。

定级符合率／%生产过程 开发设计过程定点规定 结论A ＞92 ＞90 可给予 没有严重的单项薄弱环节B 82～91 79～89 有条件的给予 在开发／SOP开始之前可落实改进计划／投资计划C ＜82 ＜79 不给予 无法估计／不能在开发／SOP之前落实改进计划／投资计划

2.1 利用改进的AHP确定各评价指标的权重

利用改进的AHP——三标度法，决策者能较容易地对指标重要性程度做出比较，尽可能减少判断矩阵的主观臆断性，提高判断准确性，并能够很好地解决判断矩阵的一致性问题，使评价的结果更为客观和准确，从而取得更好的应用效果［3］。

2.1.1 三标度法求判断矩阵 对于多层次评价指标体系中各层次上的元素依次进行两两比较，建立如式（1）的比较矩阵A见表3。

yi为各元素的重要性程度排序指数，用ymax和ymin表示最大和最小排序指数，对应的元素为Amax和Amin。选取Amax和Amin作为基点比较，经决策者比较，用某种标度给出这个基点的相对重要程度bm（bm＞1），求出判断矩阵B。

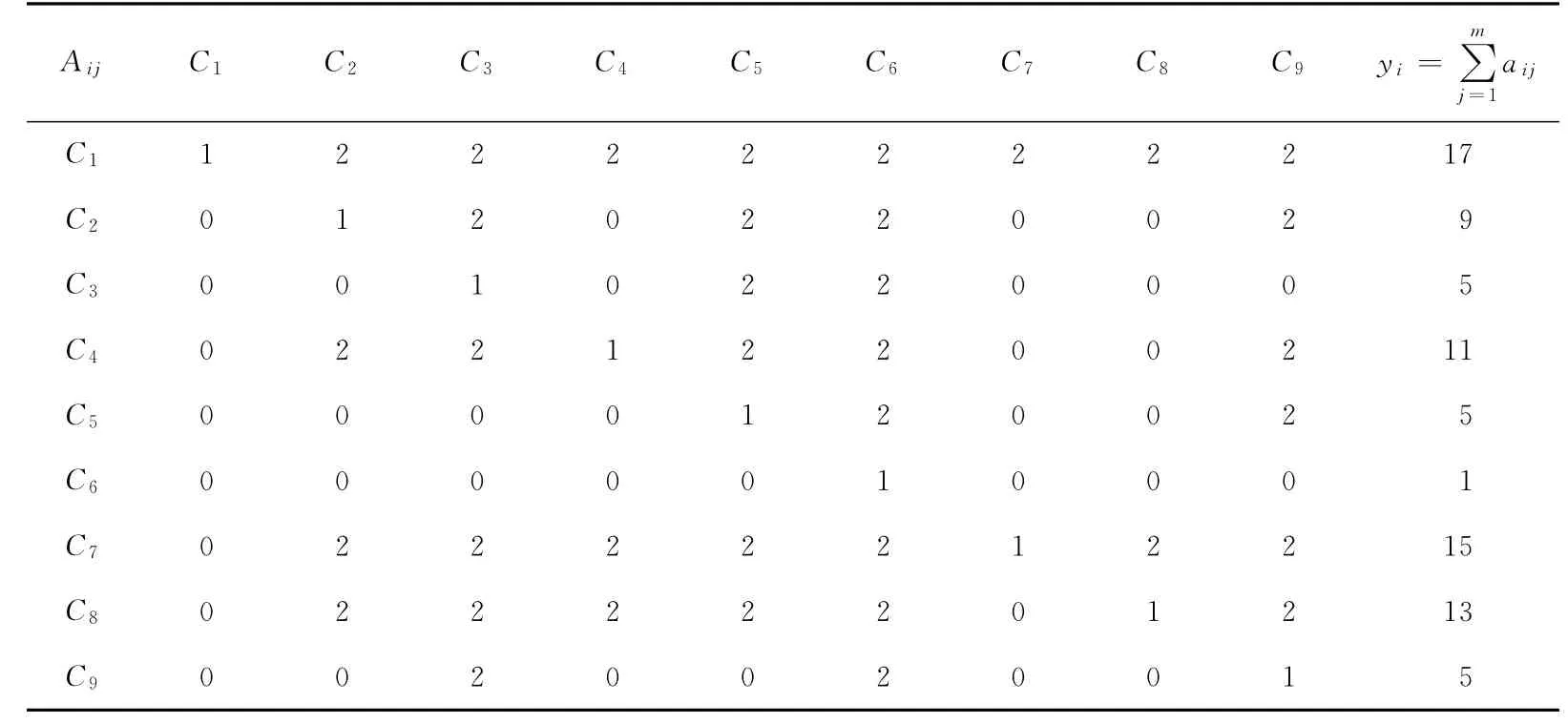
表3 “生产过程”末级指标比较矩阵Table 3 “Productive process”final stage index comparative matrix

对上述供应商评价体系中“生产过程”的9个末级指标，根据式（1）和（2）两两比较得到比较矩阵，bm取7，求出判断矩阵B，结果见表4。

表4 “生产过程”末级指标判断矩阵Table 4 “Productive process”final stage index judgment matrix

2.1.2 末级指标权重求解与一致性检验 由式（3）求出各末级指标权重Wi。 为提高决策的科学性，检验专家对各指标评价意见的一致性，对判断矩阵进行一致性检验，一致性指标CI如式（4）所示，其中，λmax为最大特征值。当一致性比例CR≤0.1时（RI为随机一致性指标［5］），判断矩阵基本符合完全一致性条件，否则要调整判断矩阵元素的取值。

为采用层次分析软件yaahp来计算各指标权重值及一致性的检验，计算结果见表5。

2.2 灰色理论综合评价

2.2.1 评价灰类及评价样本矩阵 将各指标的取值范围也相应地划分为s个灰类［6，7］，将指标的取值范围［X1，XS＋1］划分为s个区间［X1，X2］，…，（Xn－1，Xn），…，［XS－1，XS］，［XS，XS＋1］。文章所划分的灰类参照该整车厂供应商评价体系，分为A、B、C 3个灰类，各指标总分为10，“生产过程”3个灰类范围依次为（9.2，10］、［8.2，9.2］、［0，8.2）。

表5 “生产过程”末级指标权重Table 5 “Productive process”final stage index weight

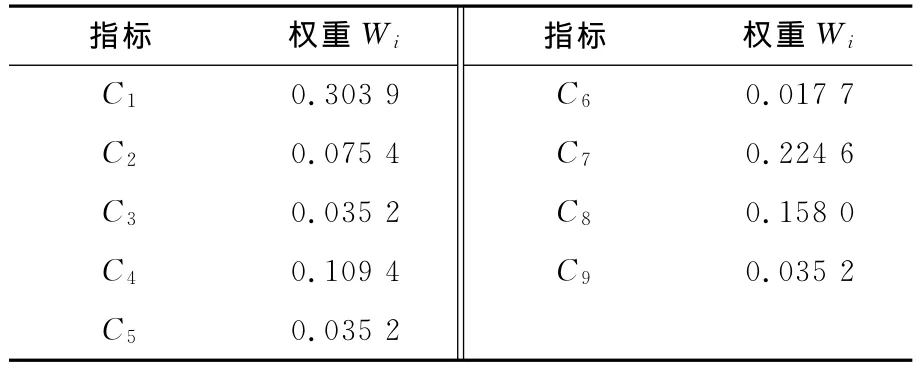
表5 “生产过程”末级指标权重Table 5 “Productive process”final stage index weight

一致性CR ＝0.030 3＜0.1。

指标 权重W i C 1 0.303 9指标 权重W i C 6 0.017 7 C 2 0.075 4 C 3 0.035 2 C 4 0.109 4 C 5 0.035 2 C 7 0.224 6 C 8 0.158 0 C 9 0.035 2

运用专家打分法来求得对供应商的评价样本矩阵，邀请4位专家对“生产过程”9个末级指标分别打分，得出评价样本矩阵：

2.2.2 白化权函数 白化权函数的确定是灰色聚类方法的关键。白化权函数一般设计为单调函数，并用直线来简化表示评价类别这一灰数受“偏爱”的程度。

令λn＝ （Xn＋Xn＋1）／2属于第n个灰类的白化权函数值为1，连接（λn，1）与n－1个灰类的起点Xn－1和n＋1个灰类的终点Xn＋2，得到第i个指标关于n类灰类的三角白化权函数fn（dij）。对于f1（dij）和fs（dij），可分别将i 指标取数域向左、右延拓至 X0，X，根据灰类范围的划分，得出n个白化权函数，“生产过程”白化权函数见图2。ABC 3个灰类的白化值C1＝ ［9.7，8.7，7.7］T。

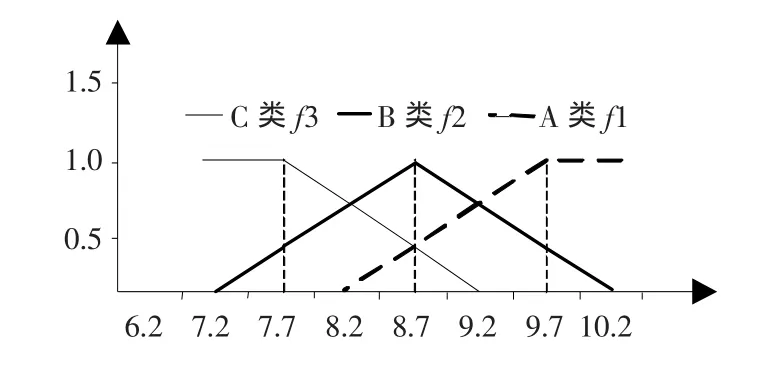
图2 “生产过程”白化权函数Figure 2 “Productive process”whitening weight function

2.2.3 灰色评价权矩阵 根据s个灰类白化权函数，求出D1中的每一个元素dmi所得出的n类灰类的白化值fn（dmi），其中n ＝ （1，2，3，…，s），（m ＝1，2，3，…，t），根据式（7）和（8）分别求出末级指标Ci第n类灰类统计值汇总Nin与其总灰类统计值的汇总Ni。

将式（7）与（8）相除，计算得到指标Ci灰色评价权rin，由此可以得到灰色评价权矩阵。

对于“生产过程”的9个末级指标，得出灰色评价权矩阵R1，见表6。

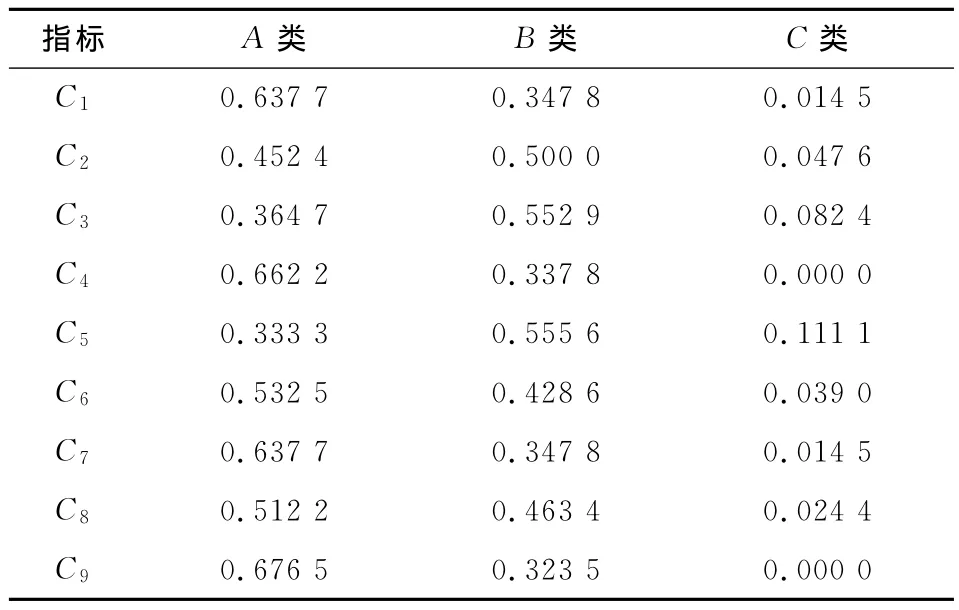
表6 “生产过程”末级指标灰色评价权矩阵Table 6 “Productive process”final stage grey evaluation weight matrix

2.2.4 综合评价 根据已求出的各项末级指标权重Wi和灰色评价权矩阵R，计算综合评价集B［9］，计算得到综合评价值S。

根据式（9）和（10），可确定供应商所属灰类等级，并得到“生产过程”综合评价值S1：

重复上述算法可得“开发设计过程”综合评价值S2，“开发设计过程”3个灰类范围依次为（9.0，10］、［7.9，9.0］、［0，7.9）。

由此可以判定该供应商的“生产过程”和“开发设计过程”均属于A灰类，获得A级供应商资格。

3 结论

（1）结合某机械制造企业的供应商评价指标，通过改进的层次分析法确定了各单项指标的权重，考虑到多名评审员评价样本信息的不规律性，建立了白化权函数得出灰色评价权矩阵，确定了供应商所属灰类等级。

（2）采用灰色层次分析法能较系统真实地反映出所评价的供应商的整体运营情况，该方法对零部件供应商的体系管理、产品质量等也可以进行有效评价，有利于机械制造企业与其零部件供应商建立并维持良好的合作关系。

1 Sehmitz J，Platts K W.Supplier logisties Performance measurement：Indication from a study in the automotive industry［J］.International Journal of Production Economics，2004，89：231～243.

2 李月南.基于灰色层次分析法的供应商评价研究［J］.物流科技，2012（6）：44～47.

3 陈实.供应链中零部件供应商的评价与选择［J］.汽车工业研究，2008（5）：31～35.

4 左军.层次分析法中判断矩阵的间接给出法［J］.系统工程，1988（6）：56～63.

5 杜利珍，陶德馨.基于AHP和TOPSIS的零部件供应商评价系统［J］.物流工程与管理，2011（3）：63～64.

6 邓聚龙.灰色系统理论教程［M］.武汉：华中理工大学出版社，1990：100～120.

7 王凤忠.基于灰色层次分析法的应急物流保障能力评价［J］.军事物流，2011（9）：226～229.

8 刘思峰.基于改进三角白化权函数的灰评估新方法［J］.系统工程，2011（2）：244～250.

9 李志平.基于灰色层次分析法的供应商评价选择应用研究［J］.石家庄铁道大学学报，2012（4）：13～18.