把握数学广角复习脉络 彰显数学思想和方法

李凤丽

伴着新年钟声，学校的第三轮课改已经如火如荼的开展起来。其中年级组的优秀课例展示让我记忆犹新，特别是老师们指教的“数学广角”更是历历在目。回想去年自己刚上过六年级，心中不禁有一种冲动：好好钻研数学广角教材，认真拜读优秀课例，借鉴他人成熟的教学理念，以便在六年级下期的整理复习中把握数学广角复习脉络，彰显数学思想和方法，促进师生的共同发展。

数学广角是新课标教材最引人注目的亮点，是传承和引领新课标理念的重要载体，是实现“基本知识、基本技能、基本思想、基本活动经验”四大目标体系之一“基本思想”的快捷通道，更是学生感悟体会数学方法和策略的有效途径。由于数学广角在1-6年级是分散安排的，加之学生对知识遗忘性较大，所以在六年级下期的总复习中，如何梳理数学广角的知识，把握数学广角复习脉络，彰显数学思想和方法这个命题就尤为重要。笔者根据自己的教学经历，总结出如下的复习策略。

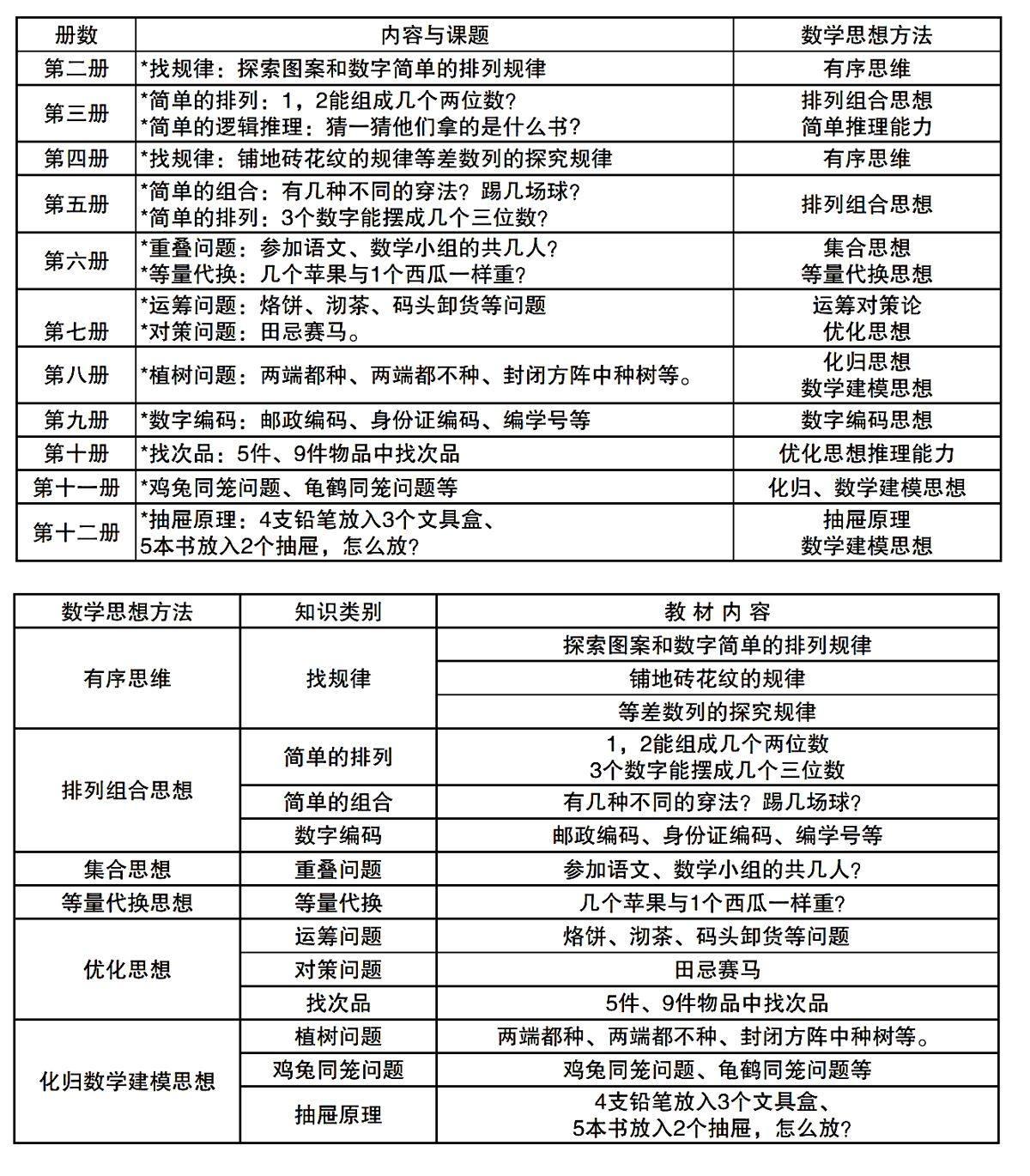
一、师生重温教材，把握数学思想

二、师生共同构建，内化数学思想

建构主义理论认为，知识是由认知主体通过新旧经验的积极互动建构起来的。学生的学习不是被动接受的过程，而是主动建构的过程。学生不是空着脑袋走进教室的，他们一开始就将自己的信念、理解、文化实践带进学习中，并且在学习过程中建构自己的意义。由于数学广角的内容很丰富，所以我认为可以充分发挥小组合作学习的强大功能，对数学广角进行大板块式的建构，从而使数学思想扎根于学生的脑海中。

1、从知识的侧重点与四大领域的交叉性来讲：

“数学广角” 其原型是属于奥数训练课，不属于“四大板块”内容，根据他们的内在联系又可以融入四大板块之中，所以我认为可以这样建构：

①探索图案和数字简单的排列规律、简单的数字排列、等差数列的探究规律、简单的组合问题、数字编码以及鸡兔同笼问题等可纳入“数与代数”；

②铺地砖花纹的规律、重叠问题、植树问题可纳入“空间与图形”

③烙饼、沏茶、码头卸货等运筹问题、找次品、对策问题可纳入“统计与概率”

④简单的逻辑推理、等两代换、抽屉原理可纳入实践于综合应用部分。

2、从数学思想方法层面来构建：

以上的建構方法虽是一家之言，但只要坚持以学生为中心，引导学生对知识的主动探索、主动发现和对所学知识意义的主动建构，就可以为我们研究数学广角、领悟数学思想，掌握数学方法，寻找优化策略等提供了强有力的建构策略。

三、立足数学思考，提升数学思想。

“数学思考”就是在对数学进行比较深刻的、周到的思维活动，主要指学生思考问题中所表现出来的条理性、逻辑性以及合情推理能力。细心的老师一定会发现，一直在教材中以“数学广角”为标题的内容到六年级下期总复习时就上升为“数学思考”（第91页），我想这正是编者要大声告诉我们的，数学思想和方法是学生长期进行有效的数学思考的结晶，而数学思考又正是渗透和提升数学思想和方法的灵丹妙药，所以编者说出了这样一句引领我们教学行为的经典话语：“数学思想方法可以化难为易，帮助我们解决问题。”因此在进行数学广角的复习中，立足数学思考的灵活性、敏捷性、深刻性，用好教材的三个例题，为提升学生数学思考的能力奠定基础。

1、把握三个例题的脉络，发挥例题的引领作用

第91页的数学思考的总复习中教材只提供了三个例题。这三个例题可以说不仅仅是复习的蓝本，更是沟通知识联系、培养学生思考习惯、提高解决问题能力的活动素材。例4是一个比较典型的找规律，启发学生从2个点、3个点开始寻找规律，通过画一画、数一数、算一算、比一比等数学活动逐步探索出：线段的总条数=点数×（点数-1）÷2，而这一规律的发现就较好地展示了有序思维的条理性，从而巩固、发展学生找规律、分步枚举组合以及列表推理的能力。例5以选送节目为题材，讨论怎样分两步找出组合数，再求选送方案的总数，渗透了作为排列组合基础之一的乘法原理。而这个乘法原理的探究完全体现了学生的自主参与，无论采用何种方法，只要有顺序地思考，做到重复或遗漏，这样发现乘法原理的奥妙所在。例6是一个比较复杂的逻辑推理问题，教材渗透了逻辑推理的常用方法“排除法”。学生借助列表法，用数字或符号逐步缩小范围，根据题里的相关条件进行简单的推理，从而较好地培养学生的逻辑思维能力和口头表达能力。

2、把握数学思考的实质，拓展数学思想的视野

数学思考是数学基础教育的核心目标。其核心是指“在解决问题的过程中，使学生能进行简单的、有条理的思考”。因此我在上述三个例题的处理的基础上，适度地进行了数学问题视野的拓展，让学生尝试用符号来表达自己的想法，经历了从实物到抽象的数学化的思考过程，从而感受数学思想方法的强大魅力。比如在例4后面我增设了“数直线上的线段、数从同一点引出多天射线的角、数三角形、数长方形、数长方体”等相关的探究活动，进一步感受规律的科学性和普遍性；在例5后面我增设了加法原理，让学生通过对比初步明确加法原理和乘法原理的区别；在例6后面我增设了“猜职业、猜名次、猜正方体的对面”等实践活动，让学生初步学会抓住矛盾的双方进行有效的排除，引导学生“有条理地思考、有价值地取舍”，让数学思想方法在学生脑海中生根发芽、开花结果。

总而言之，虽然数学广角与其他四大领域的知识相比所占的比例很小，但它在新课标教材中同样扮演着“经历探究过程、建构数学模型、体验数学思想、掌握数学方法、提升数学素养”的重要角色。正是有了这些数学规律的发现，有了数学问题的解决，才有了用数学思想方法链接的“数学高速”。我想作为数学广角的总复习，它所带给我们的将是更经典的数学文化，提供为我们的将是更美丽的舞台。有句广告词说得好，“心有多大舞台就有多大”，让我们在这个美丽的舞台上，舞起数学思想方法的彩绸，和学生们一起在数学天地了翩翩起舞，共享人生！

参考文献

[1]《数学新课程标准》实验稿2001年出版，修订稿2007年4月

[2]金文钦 “数学广角，想说爱你不容易”