一类双线性SEIQS模型的定性分析

崔 宁

（河北建筑工程学院数理系，河北 张家口075000）

0 引 言

现实生活中人们面临着许多传染病的威胁，数学模型在分析疾病的传播和控制措施的制定中起着非常重要的作用，而隔离一直作为有效的措施应用于H1N1、HIV／AIDS、SARS［1－3］等疾病控制中.将总人数分为易感者类S、潜伏者类E、感染者类I和隔离者类Q，本文将研究具双线性传染率［4］的SEIQS模型

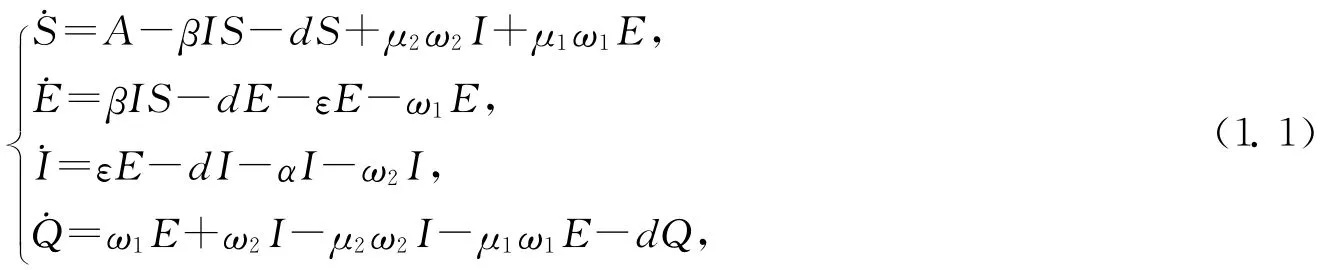
这里，易感者来源分为常数迁入率A和对潜伏者和感染者的有效治愈率μ1ω1E、μ2ω2I，其中，ω1和ω2分别代表对潜伏者和感染者的隔离率；各舱室类的自然死亡率为d；因病死亡率和潜伏期的发病率分别用α、ε表示.

显然，我们只需考查（1.1）的子系统

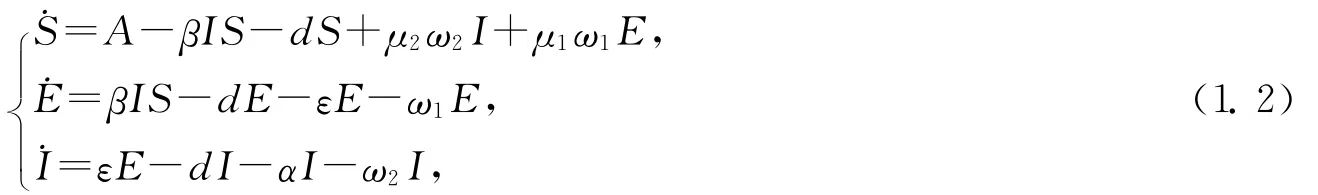
由（1.2）可得

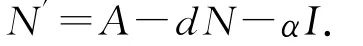
因此

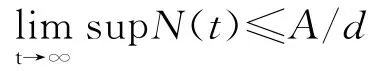
所以系统（1.2）的不变集为

定义D的边界和内点集合分别为∂D和°D，经过简单计算可得系统存在两个正平衡点：无病平衡点P0＝（A／d，0，0）∈∂D和地方病平衡点P1＝（S1，E1，I1），其中

S1＝（d＋ε＋ω1）（d＋α＋ω2）／（εβ），I1＝I0（R0－1），E1＝（d＋α＋ω2）I1／ε，为系统（1.2）的基本再生数，由此可得结论

定理1R0≤1时，P0为D内的唯一平衡点；R0＞1时，内存在唯一的地方病平衡点P1.

1 全局稳定性

引理1 若R0＞1，选取充分大的t＞0，存在紧吸引集，当t＞t时，沿系统（1.2）过初值（S（0），E（0），I（0））∈K的解（S（t），E（t），I（t））均有βS（t）＞μ2ω2成立.

证明 由系统（1.2）可得

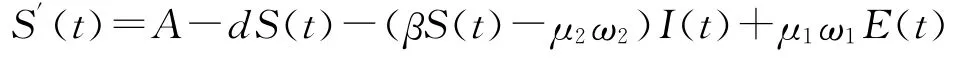
若βS（t）≤μ2ω2，应有S′（t）≥A－dS（t）≥A－dμ2ω2／β，注意到R0＞1，所以

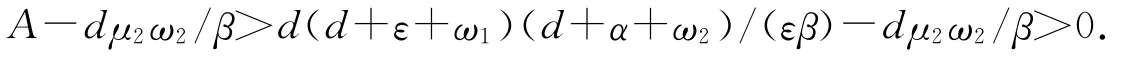
可知（1.2）的所有解在无穷远处都经过直线βS（t）＝μ2ω2并最终保留在直线之上，因此，对于充分大的t＞0，当t＞t时，βS（t）≥μ2ω2对于过初值（S（0），E（0），I（0））∈K的解（S（t），E（t），I（t））均成立.证毕

定理2 （i）当R0≤1时，D内存在唯一的无病平衡点P0，且全局渐近稳定；（ii）当R0＞1时，°D内存在唯一的地方病平衡点P1，P0不稳定.

证明 构建函数

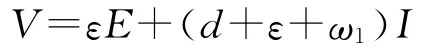
对函数沿着（1.2）的解求导数，当R0≤1有

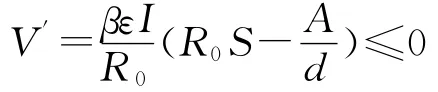
此外，当且仅当I＝0时，有V′＝0，在｛（S，E，I）∈D∶V′＝0｝上的最大不变集为单点集｛P0｝.因此，由LaSalle不变集原理［5］可知，当R0≤1时P0全局渐近稳定.同时I＞0时，有V′＞0，及可S＞A／（dR0）知结论（ii）成立.证毕

定理3 当R0＞1时，°D内唯一的地方病平衡点P1全局渐近稳定.

证明 通过上述结果，可知系统（1.2）在可行集D的内部满足文献［6］中的条件（H1），（H2），系统的加法复合矩阵为

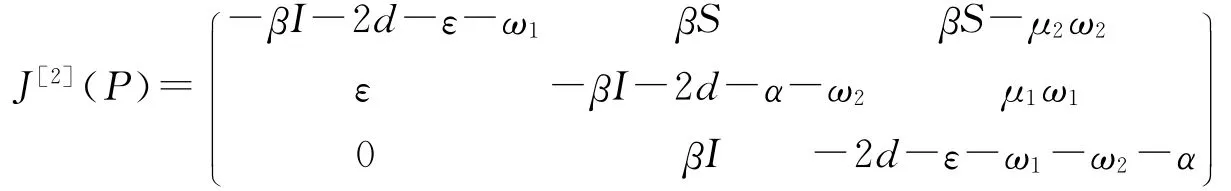
定义函数

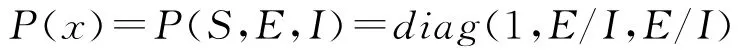
矩阵

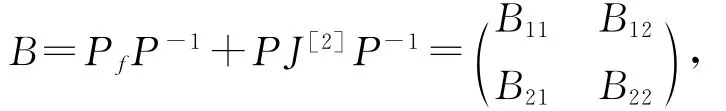
经计算得

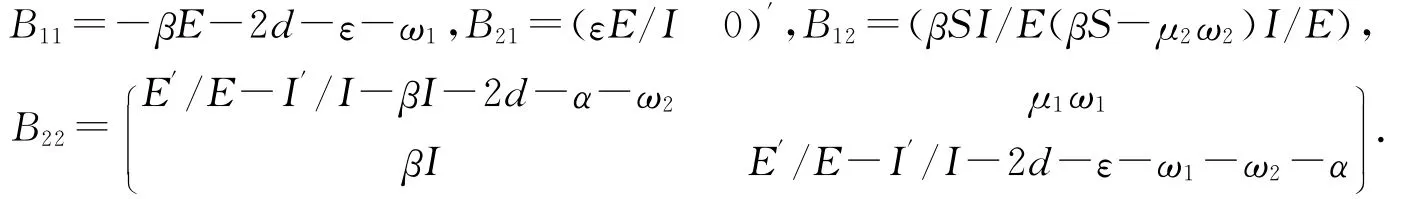
将（u，v，w）定义为的向量，选择R3中的范数，并把ρ记为该范数的Lozinskii测度，结合文献［7］可估计ρ（B）≤sup（g1，g2），这里

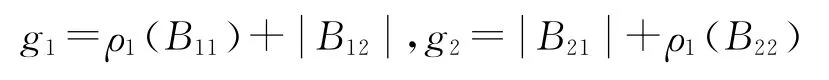
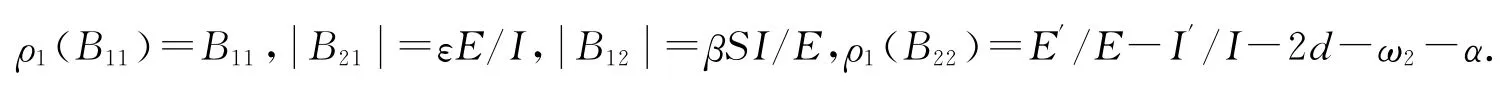
由系统（1.2）可得

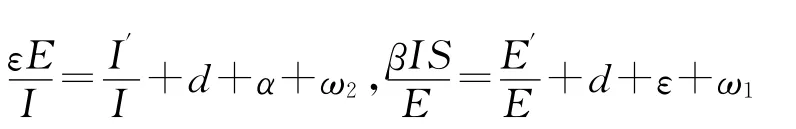
因此，选择充分大的t使得

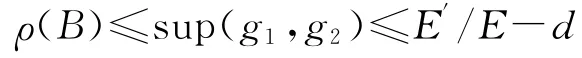
对t＞t成立.所以，存在一吸引集K，使得沿系统（1.2）过初值x0∈K的解有

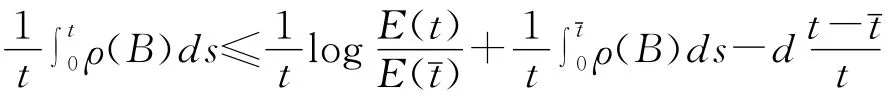
从而可知q2≤－d／2＜0成立.所以°D内唯一的地方病平衡点P1全局渐近稳定.证毕

2 仿 真

接下来我们讨论系统极限环的存在性，我们取参数值为

A＝0.1，μ1＝μ2＝w1＝w2＝0.0001，α＝ε＝0.1，d＝0.0001，β＝0.0011，

则系统存在地方病平衡点P1＝（3.6728，5.1087，25.4165）.经计算得Jacobian矩阵的特征根为－0.684， －0.0337i， 0.0337i，

显然，此时系统出现Hopf分支.所以，结合文献［8］，当β1＝0.001＜β时，系统在地方病平衡点P1附近出现极限环，如图1.

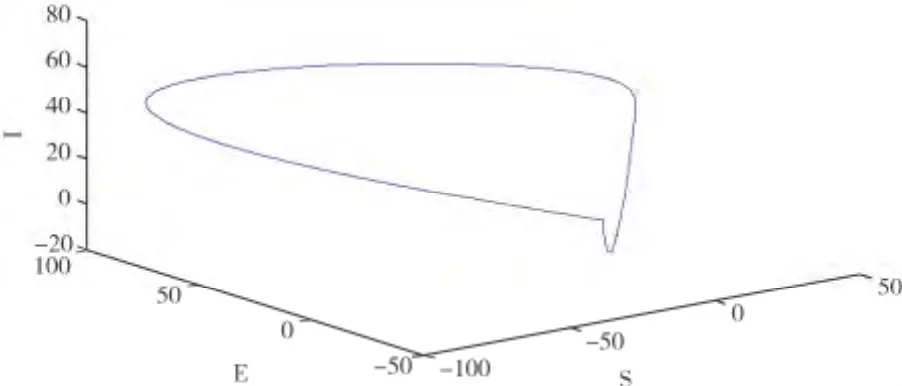
图1 系统极限环现象

［1］Hong Xiao，Huaiyu Tian，Lei Shao etc，Spatio－temporal Simulation of Epidemiological SIQR Model Based on the Multi－Agent System with Focus on Influenza A（H1N1）.Communications in Computer and Information Science，107（2010）：180～189

［2］Ram Naresh，Agraj Tripathi，Dileep Sharma，Modelling and analysis of the spread of AIDS epidemic with immigration of HIV infectives.Mathematical and Computer Modelling，49（2009）：880～892

［3］Ying－Hen Hsieh，Chwan－Chuan King，Cathy W.S Chen etc，Impact of quarantine on the 2003SARS outbreak：A retrospective modeling study.Journal of Theoretical Biology 244（2007）：729～736

［4］W.Wang，S.Ruan，Bifurcation in an epidemic model with constant removal rate of infectives，J.Math.Anl.Appl.291（2004）775～793

［5］J.P.LaSalle，The Stability of Dynamical Systems，SIAM，Philadephia，PA，1976

［6］M.Y.Li，J.S.Muldowney，A geometric approach to global－stability problems，SIAM J.Math.Anal.27（1996）1070

［7］R.H.Martin Jr.，Logarithmic norms and projections applied to linear differential systems，J.Math.Anal.Appl.45（1974）432

［8］NA YI，ZHIWU ZHAO，QINGLING ZHANG，Global Analysis of an Epidemic Model with general Incidence Rate，International Journal of Information and systems Sciences，5（2009）296～310