基于数学模型的城市内涝灾害风险评估研究

2014-04-29邓全才王利民马立山郝桂珍

河北建筑工程学院学报 2014年4期

关键词：内涝积水灾害

邓全才王利民马立山郝桂珍

（1.河北建筑工程学院数理系；2.河北建筑工程学院研究生部；3.河北建筑工程学院能源与环境工程学院河北张家口075000）

0 前言

随着全球气候的不断变化和城市化的快速发展，城市的洪涝灾害发生的概率在大大增加，波及的范围也越来越大.洪涝灾害已经成为人类社会共同面临和关注的重大问题，对洪涝灾害的研究也成为国内外学者研究的重点内容［1］［2］.

1 内涝灾害的成因

自然水循环系统和社会水循环系统构成了城市水循环系统（如图1），城市内涝正是水循环出现问题的表现，是自然因素和认为因素共同作用的结果.自然因素方面，全球气候变暖，加强了暴雨产生的概率，社会因素方面，城市化的快速发展引起的城市“雨岛效应”和“热岛效应”，增加了城市降雨频率与强度［1］.另外，城市不透水面积的增加、排水管网排水标准低、排水系统雨污混接、地面沉降、管理体制不健全、城市功能区规划不合理等也是造成城市内涝的主要因素［3］.

图1 城市水循环系统

2 内涝灾害的评估

内涝灾害风险评估分为灾前评估、灾中评估和灾后评估.评估的主要方法有：数理统计法、指标体系法、仿真模拟法、综合评定法和决策分析法.评估主要是从致灾因子、承灾体的脆弱性和暴露分析三个方面进行评估.灾害风险公式为：

其中，H为特定区域在某段时间发生破坏性的自然现象，V为某种要素在强度不同的自然现象下所造成的损失程度，E表示暴露在风险中的各种要素，如人、财产等［4］.

内涝灾害的风险评估是一个动态的过程，可以通过以往的评估为本次的评估提供依据，提高评估的准确性，同时，本次评估又可以为下次评估的改进提供了新的数据和理论支撑.通过这种不断循环，周而复始，可以及时修正、更新评估策略，为内涝灾害的风险评估提供可靠的依据.

3 数学模型的构建

3.1 基本原理及其网格划分

城市内涝数学模型以地表与明渠河道水流运动为主要模拟对象，其中平面二维非恒定流的基本方程为基本控制方程的骨架.同时，针对小于离散网格尺度的排水渠系或河道，在二维模型中结合一维明渠非恒定流方程的算法.

传统的数值模式计算，通常采用规则网格或拟一致的三角形网格对计算区域进行剖分.但是城市局部地区地形复杂，街道、河流分布、建筑物构造形式等差异较大，对暴雨后形成的地表径流影响较大.因此，为了更好的反应暴雨后地表径流，模型采用有限体积法，采用无固定结构且不规则的网格.因地制宜，将网格设计成三角形、四边形或五边形等.网格的的边为通道，网格单元为控制体，在网格中心计算水位H，H是该网格的一个平均值，在通道的中点处计算流量Q，Q是该通道的一个平均值.同时，水位和流量在时间上采取时间交错计算方式.

3.2 动量离散方程

连续方程根据高斯定理转化为：

其中，Hi为i单元水深，Lik为i单元第k条通道长度，即多边形网格的边长，Ai为i单元网格面积，Qik为i单元第k条通道上的流量，qi为i单元的源或汇，dt为t时刻的时间增量.

Qik按简化的动量方程离散格式计算.在平面浅水运动中，对流项作用很小，可以忽略不计，但对不规则网格，如果严格按照动量方程计算任意方向通道上的流量，计算量较大.模型中采用分类简化处理的方法.假设在同一时间内，同一网格的水位波动不大，然后采用分类处理的方法求任意网格各个通道上的单宽流量.通道分为路面型、特殊通道型（城市内二级河道）、其他型（堤坝、泵站、闸门、淹没出流管道等），根据不同类型简化动量方程，计算流量［5］［6］.

河道型通道的动量离散方程为：

其中，dLik为i单元第k条通道两侧单元形心距离，Zik1、Zik2分别为i单元第k条通道两侧1、2断面的水位，g为重力加速度，nik为i单元第k条通道上的糙率.

地面型通道的动量离散方程为：

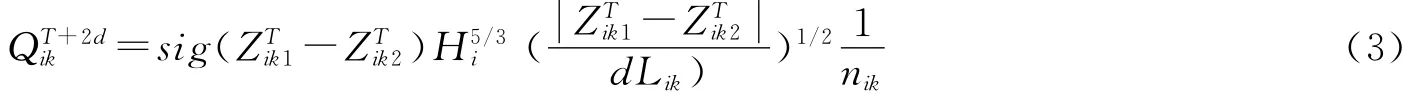
有连续或缺口堤的通道，其流量采用宽顶堰流公式计算［6］，如下：

其中，δik为i单元第k条通道下游淹没系数，mik为第i单元第k条通道的流量系数.

城市内较窄河道为特殊通道，它与两侧网格之间的流量，采用宽顶堰流公式（4）计算；沿河道单宽流量Qs采用与河道型通道动量离散方程式（2）相似的公式进行计算，特殊单元的水深按以下离散格式计算：其中，Hdi为i特殊单元的水深，Adi为i特殊单元的面积，Qdig为i通道周边的单宽流量，Ldij为i通道周边的边长,为沿通道上的流量和，qdi为i特殊单元上的源汇项，即特殊单元上的降雨强度，可取特殊点处的降雨强度作为整个单元的平均值.

4 实验及分析

4.1 阳原县地理信息概话

阳原县县城属于近几年内发展起来的小型城市，城市是在原有村镇的基础上建设起来的，因此其城市管网很不完善，大多数城市排水体系类似农村排水体系，采用暗沟的形式对城市污水和雨水进行收集排放.

根据阳原县的地形、地貌特点，对县城中心地区以及容易积水地区采用较密的网格，对于城市边缘或不易发生内涝的地区采用较稀疏的网格.因此，划分了三边形、四边形、五边形、六边形等不同的网格.共划分497个不规则网格，计算通道1283个，节点683个，部分网格单元的分布如图2［7］.

图2 网格设计示意图

对2013年8月9日阳原县降雨进行模拟，根据气象部门的数据当日的降雨量最大为100.9mm.对各个划分的网格单元的计算水深和实际水深的误差进行统计，实测水深值和计算深值的误差绝对值如表1所示.

表1 实测水深与计算水深的绝对误差的分布

由表1可见，模拟的积水误差主要分布在2cm以内，大约占85%，但是不能忽略还有12%的网格模拟的积水误差大于3cm.通过分析表明，在这些大于3cm的误差中，86%为计算积水偏小.因此，通过此模型能够良好的预测降水量，使得在内涝灾害评估中及时发现安全隐患，在一定程度上减少人员财产的损失，保护了国家和人民的利益.